Rebondissement des nanoparticules de silice hydroxylée :une étude atomistique basée sur les potentiels REAX

Contexte

Les collisions de nanoparticules de silice (NPs) jouent un rôle important dans de nombreuses branches de la géophysique et des sciences planétaires. Des exemples sont fournis par la physique des dunes de sable sur Terre et sur d'autres planètes [1]; dans les disques protoplanétaires autour des étoiles naissantes, les collisions entre particules de silice constituent le premier processus sur l'étape de la formation des planètes [2, 3]; dans les systèmes solaires matures, les sources de particules de poussière sont disponibles par émission de comètes [4, 5] ou collisions d'astéroïdes [6-8]. De plus, les collisions de silice NP servent également d'exemple prototype de mécanique granulaire et sont donc utilisées dans des expériences visant à comprendre la physique des collisions NP [9–12]. Habituellement, les paramètres du matériau décrivant les grains de silice sont tirés de données expérimentales. Ici, les propriétés en vrac telles que les modules d'élasticité sont sujettes à peu d'erreurs, tandis que les propriétés de surface, en particulier l'énergie de surface spécifique, sont sujettes à des fluctuations considérables entre les expériences individuelles [13]. L'énergie de surface entre dans des quantités importantes telles que la probabilité de collage et le transfert d'énergie lors des collisions.

Ces fluctuations sont induites par les adsorbats, en particulier l'eau, qui sont couramment présents à la surface des grains. La silice étant un matériau polaire, les adsorbats ou leurs produits de dissociation peuvent passiver les liaisons pendantes à la surface des grains, modifiant ainsi fortement l'énergie de surface.

Les simulations atomistiques basées sur les interactions interatomiques visent à aider à la compréhension des processus de collision NP. Cette approche n'est pas triviale dans le cas de matériaux polaires comme la silice, où les adsorbats peuvent fortement influencer les interactions en surface [14]. Ainsi, il a été constaté que lors de la modélisation de collisions de silice avec des surfaces propres, les NP en collision collent plutôt que de rebondir sur une large gamme de vitesses [15], contrairement aux expériences [16–18]. On peut supposer [13] que la passivation superficielle par l'eau, c'est-à-dire l'hydroxylation superficielle, est responsable de ce comportement. Jusqu'à présent, les simulations de collisions de NP de silice passivée ne pouvaient être effectuées qu'avec de petits grains (≤ 2 nm) [19], qui montrent une dispersion considérable des résultats de collision en raison de leur taille nanoscopique.

Nous voulons démontrer ici l'effet de l'hydroxylation de surface sur les collisions de NP de silice en comparant directement les résultats des NP hydroxylées avec ceux obtenus précédemment pour la silice propre [15]. Cela nous permettra de conclure que l'effet de l'hydroxylation sur les propriétés collisionnelles peut être capturé par une diminution de l'énergie de surface spécifique.

Méthode

Nous utilisons le potentiel REAX pour modéliser les interactions interatomiques entre Si, O et H [20]. Bien que ce potentiel soit plus d'un facteur 100 plus lent que les potentiels de paire, il a l'avantage d'inclure van der Waals et les interactions électrostatiques ainsi que les liaisons covalentes dans un cadre et appartient donc aux potentiels interatomiques les plus avancés disponibles [21]. Il a été conçu dans le but particulier d'inclure des réactions chimiques dans les simulations MD classiques et ainsi d'aider à combler le fossé entre les simulations classiques et quantiques [22]. Par conséquent, ce potentiel nous permet de capturer les ruptures de liaisons et les formations qui peuvent se produire lors de collisions à haute énergie à la fois dans la silice et dans la couche superficielle hydroxylée. De plus, il permet de modéliser le processus d'hydroxylation, c'est-à-dire l'interaction O-H et OH-Si.

Pour produire les NPs, nous utilisons la silice amorphe qui a été préparée récemment [15] selon la procédure de trempe décrite par Huff et al. [23]. Ce bloc de silice a été relaxé dans le potentiel REAX et les sphères de rayons R =10, 15 et 20 nm - contenant respectivement 0,32, 1,01 et 2,38 millions d'atomes par sphère - ont été coupés de cet échantillon et relaxés à la température finale de 200 K. Cette température a été choisie car elle est typique de la ceinture d'astéroïdes. dans le système solaire; cependant, on ne s'attend pas à ce que la température modifie fortement la dynamique de collision tant qu'elle est inférieure à la température à laquelle la couche d'hydroxylation commence à se dissoudre (460 K) [15, 24].

L'hydroxylation de surface est réalisée de manière similaire aux études précédentes sur l'interface silice-eau [19, 25-28]. Nous identifions les atomes O et Si sous-coordonnés à la surface NP; H est ajouté à O sous-coordonné et OH à Si sous-coordonné; dans les deux cas, des groupes silanol terminaux (-SiOH) sont ainsi créés. Le NP hydroxylé est ensuite autorisé à se détendre en utilisant un algorithme de gradient conjugué. La densité surfacique des groupes silanol créés à la surface s'élève à 4,12 (4,93, 4,89) nm ⁻² pour le R =10 (15, 20) nm sphère. Les densités expérimentales de silanol sont comprises entre 2,6 et 4,6 OH nm ⁻² [24]. D'autres études de simulation ont donné des valeurs inférieures, 2,0 à 2,5 OH/nm ² [25, 27] ou même seulement 1,3–1,8 OH/nm ² [19], mais aussi des valeurs plus élevées de 6,6 OH/nm ² [26, 28]. Cette grande variété est due à (i) une identification éventuellement incomplète des atomes de surface sous-coordonnés et (ii) une rugosité de surface atomique résultant en une surface effective plus grande que la surface calculée [26, 28]. A noter que dans l'expérience, la concentration en silanol dépend également de la valeur du pH de l'environnement [14, 29, 30]. Nous concluons que nos densités de surface de silanol ne sont pas irréalistes.

La collision est déclenchée en dupliquant le NP et en faisant pivoter les deux NP de manière aléatoire l'un par rapport à l'autre, voir Fig. 1. Pour chaque système de collision, 5 simulations sont effectuées pour collecter des statistiques ; les simulations diffèrent les unes des autres par les angles de rotation. Les deux copies sont ensuite tirées l'une sur l'autre avec une vitesse relative v . Seules les collisions centrales sont considérées. Les simulations sont exécutées jusqu'à ce que le sort final - rebond ou collage - puisse être clarifié, voir Réf. [15, 31] pour plus de détails.

NPs de silice hydroxylée. NPs de silice hydroxylée de rayon R =10 nm juste avant la collision. Rouge, Si; bleu, O lié à Si; orange, O dans un groupe OH; blanc, H

Les simulations de dynamique moléculaire sont réalisées avec le code LAMMPS [32]. Les instantanés atomiques sont générés avec OVITO [33]. La simulation d'une collision unique - pour l'exemple de R =sphères de 20 nm entrant en collision avec v =100 m/s :environ 120 h sur 256 cœurs.

Résultats et discussion

Le coefficient de restitution (COR) mesure la vitesse relative des NP après collision, v ^′ , par rapport à celui avant collision, v , comme :

Il disparaît lorsque les deux NP collent; un COR non nul peut donc être considéré comme un signe de rebond. La figure 2a montre le COR tel que mesuré dans nos simulations. Les NP hydroxylées collent à de faibles vitesses, rebondissent dans une grande fenêtre de rebond [31] jusqu'à des vitesses de 1200 m/s, puis collent à nouveau. Le blocage à de grandes vitesses est causé par de fortes déformations NP qui dissipent l'énergie et permettent aux grains en collision de fusionner.

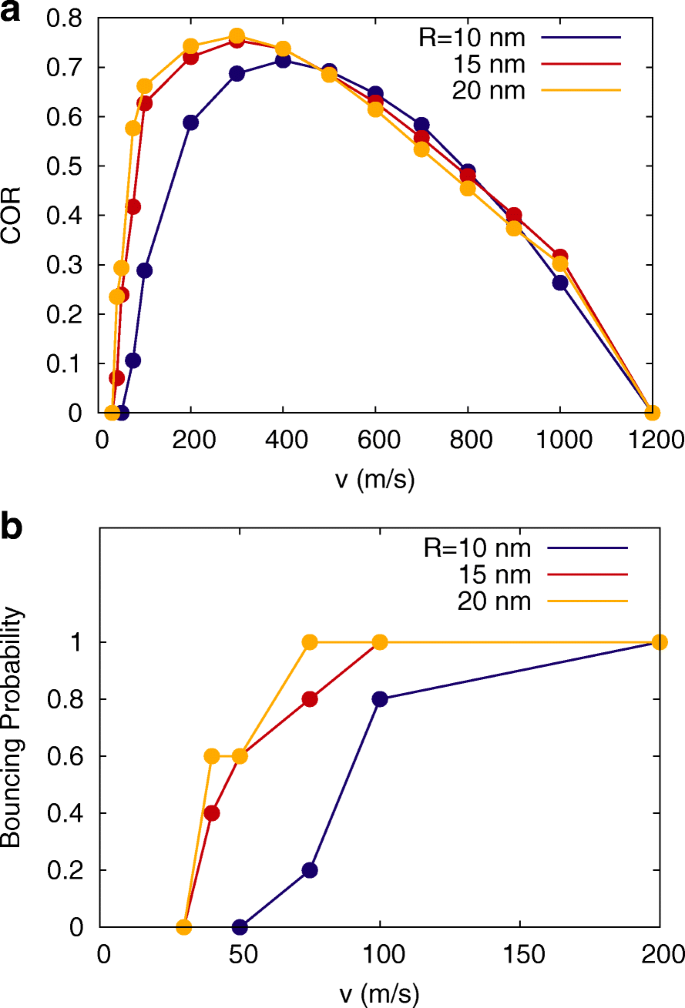
Coefficient de restitution et probabilité de rebond. un Coefficient de restitution (COR) et b probabilité de rebond en fonction de la vitesse d'impact, v , pour différents rayons NP R . Symboles, résultats de simulation. Les lignes doivent guider l'œil

En revanche, le collage à faible vitesse est causé par les forces d'adhérence entre les NP. Nous traçons la probabilité de rebond, p _b , c'est-à-dire la fraction de collisions conduisant à des rebonds dans nos simulations, à de faibles vitesses de collision sur la figure 2b. Nous identifions la vitesse de rebond comme la plus petite vitesse où la probabilité de rebond, et donc le COR, sont non nuls. Notez que la plage de vitesses, dans laquelle 0<p _b <1 - c'est-à-dire où l'orientation relative des deux sphères en collision décide du résultat de la collision - s'élargit considérablement pour les plus petits NP. Ainsi, le collage est certain pour v ≥ 75 m/s pour les grosses sphères (R =20 nm), alors qu'elle n'est certaine que pour des vitesses atteignant au moins 200 m/s pour R =sphères de 10 nm.

La théorie macroscopique Johnson-Kendall-Roberts (JKR) [34] des contacts adhésifs prédit la vitesse de rebond v _b comme [35–37] :

Cette loi est valable pour les collisions de deux NPs de même rayon R , masse volumique ρ , énergie surfacique spécifique γ , et un module d'élasticité E _ind , qui est déterminé comme E _ind =E /(1−ν ² ) du module de Young E et le coefficient de Poisson ν . Dans notre étude précédente des collisions de silice [15], nous avons déterminé ρ =2,25 g/cm ³ et E _ind =67,1 GPa ; nous utiliserons également ces valeurs ici. La constante C est sujet à une certaine incertitude, car il inclut l'effet des canaux de dissipation d'énergie - tels que la formation de défauts dans le matériau et l'excitation d'oscillations - qui ne sont pas facilement évalués [9, 13, 36-38]. L'estimation expérimentale la plus récente a été obtenue à partir d'expériences de collision avec des sphères de silice de rayon 250 et 600 nm et a donné C =57,9 [13]. Cependant, nos données de simulation pour des sphères de silice propres de rayon ≤ 25 nm [15] nécessitent une valeur de C =669 pour le montage. Cette valeur élevée est due notamment à la formation d'un collet dynamique entre les NPs lors de la collision.

L'énergie de surface spécifique γ n'est pas facile à calculer pour nos NP hydroxylées en raison de l'inhomogénéité du système. Pour une surface de silice propre, nous avons déterminé γ =1,43±0,09 J/m ² [15]. Cette valeur est en accord approximatif avec les données expérimentales de la silice propre [13].

Cependant, l'énergie de surface spécifique γ peut être obtenu à partir d'un ajustement de l'équation. 2 à nos données de simulation. La figure 3 montre que nos données concordent bien avec le R ^−5/6 dépendance de la théorie JKR. L'ajustement des données à l'équation. 2 donne une valeur de γ =0,078 J/m ² , c'est-à-dire une réduction d'un facteur près de 20 par rapport aux résultats de silice propre. Une valeur aussi faible que l'énergie de surface est en bon accord avec la gamme de données observées expérimentalement dans la silice sur laquelle de l'eau a été adsorbée et où des valeurs dans une gamme de γ =0,02–0,3 J/m ² ont été signalés [13, 24].

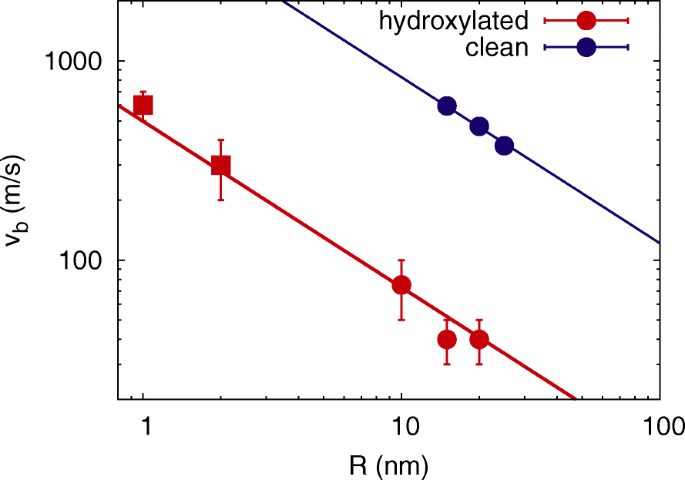
Vitesse de rebond. Dépendance de la vitesse de rebond, v _b , de NP de silice hydroxylée sur le rayon NP, R . Les données de simulation actuelles (cercle) et précédentes (carré) [19] de sphères de silice hydroxylée comparées aux données de simulation de sphères de silice propres [15]. Symboles, résultats de simulation. Ligne :Éq. 2. Les barres d'erreur des NP propres sont plus petites que la taille du symbole

Quadéry et al. [19] a-SiO₂ hydroxylé simulé de taille nanométrique NPs (rayons de 1 et 2 nm) avec le potentiel REAX et a démontré que ces NPs présentent une adhérence réduite. Ils rapportent des vitesses de rebond d'environ 0,6 et 0,3 km/s pour R =1 et 2 nm, respectivement. Ces NP avaient une structure de surface assez irrégulière, probablement parce qu'ils ont été créés en faisant fondre et en refroidissant le NP sous vide, plutôt que de les découper à partir d'un grand a-SiO₂ goûter. Lors de l'inclusion de ces données dans notre v _b (R ), Fig. 3, nous observons que ces données précédentes s'alignent bien avec nos résultats et sont décrites par l'Eq. 2 avec les mêmes paramètres.

Notez que les NP de silice propres, c'est-à-dire non hydroxylées, rebondissent à des vitesses considérablement plus élevées, cf. Fig. 3. Leurs vitesses de rebond sont à nouveau décrites avec l'équation. 2, si seulement la valeur de γ est adapté à 1,43 J/m ² , voir la ligne de la Fig. 3. Ces collisions ont été simulées dans [15] en utilisant le potentiel de Munetoh [39] pour la silice. Nous avons vérifié que pour le potentiel REAX, des résultats similaires sont obtenus. En particulier, pour le R =20 nm NP, nous avons obtenu une vitesse de rebond de 475 m/s en accord étroit avec le résultat précédent de 469 m/s [15], tandis que pour R =15 nm NPs, aucun rebond n'a été observé dans la plage de vitesse de 300 à 800 m/s.

La dynamique de collision des NPs de silice nue est caractérisée par la formation d'un col adhésif fort entre les NPs; lors de la séparation NP, ce col est dominé par des filaments, c'est-à-dire des chaînes Si-O-Si-O quasi monoatomiques. Dans la collision de NP de silice hydroxylée, la passivation des liaisons empêche en grande partie la formation de cols aussi étendus. Cependant, occasionnellement, ces cols sont également observés entre les NP de silice hydroxylée, comme nous le montrons sur la figure 4 sous la forme d'une séquence temporelle d'instantanés zoomant sur la surface de contact de deux NP en collision lorsqu'elles recommencent à se séparer après la collision. Malgré un contact étroit des deux NP (Fig. 4a), la plupart des régions se séparent à nouveau sans laisser beaucoup de changements sur les surfaces derrière (Fig. 4b); ces taches de surface inchangées sont des régions étroitement emballées avec des atomes H de passivation. Dans des régions sélectionnées, cependant, des liaisons covalentes entre les deux NP se forment (Fig. 4c), qui se développent en filaments monoatomiques (Fig. 4d) sous la forme de chaînes Si–O–Si–O qui sont décorées de groupes OH provenant de l'hydroxylation superficielle. Nous notons que la force de liaison Si-O s'élève à 4,70 eV et est donc comparable à la force de liaison O-H de 4,77 eV [40], ce qui rend les filaments ainsi que les groupes silanol difficiles à casser. Pourtant, l'un de ces filaments se brise lors de la séparation NP tandis que l'atome de Si terminal attrape deux groupes OH pour saturer ses liaisons (Fig. 4e). Cependant, la deuxième chaîne monoatomique (supérieure) ne se déchire pas (Fig. 4f). Nous avons suivi la simulation jusqu'à ce qu'il soit clair que les deux NP ont finalement été réunies à nouveau de telle sorte que cette collision particulière était une collision persistante.

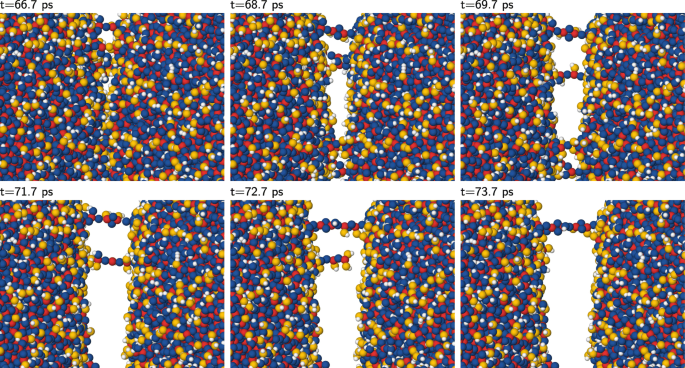
Série de clichés. Série d'instantanés — temps de 66,7 à 73,7 ps après la collision — montrant la formation de filaments temporaires entre deux NP de rayon R =15 nm après une collision avec v =75m/s. Code couleur comme sur la Fig. 1

Conclusions

Les simulations atomiques de l'interface silice-eau ne sont pas triviales en raison des processus chimiques qui se produisent. Ceux-ci conduisent à une passivation des liaisons oxygène et silicium pendantes par H ⁺ et OH ⁻ ions, respectivement. Nous utilisons le champ de force REAX, qui permet la rupture et la formation de liaisons, pour modéliser la passivation de la surface de silice. La collision de deux nanoparticules de silice hydroxylée s'écarte fortement de la collision de nanoparticules de silice nue étudiée précédemment. Alors que les nanoparticules de silice nues adhèrent à la collision pour une large gamme de vitesses de collision, les nanoparticules hydroxylées rebondissent déjà à des vitesses plutôt modestes. En comparant à la théorie JKR de collision NP, cette réduction de la vitesse de rebond peut être attribuée à la forte diminution de l'énergie de surface effectuée par l'hydroxylation.

Nos simulations ont été réalisées pour des températures NP de 200 K, bien en dessous de la température à laquelle la couche d'hydroxylation commence à se dissoudre (460 K) [15, 24]. La température que nous avons choisie s'applique à la ceinture d'astéroïdes. Leurs collisions entre astéroïdes créent une distribution à l'état stationnaire de NPs (le soi-disant disque de débris [6-8]), où des vitesses de collision de plusieurs centaines de mètres par seconde ne sont pas inhabituelles. Étant donné que la vitesse de rebond diminue avec le rayon NP comme R ^−5/6 , voir Éq. 2 et Fig. 3, nos résultats sont également pertinents pour les grains plus gros à des vitesses de collision proportionnellement plus petites.

Les recherches futures viseront à étendre la présente étude aux systèmes noyau-coquille silice-glace. De tels systèmes constituent une espèce importante de particules de poussière dans les systèmes planétaires au-delà de la ligne des neiges, et leur physique de collision sera régie par les propriétés à la fois du noyau de silice dure et de la coquille de glace d'eau plus douce.

Disponibilité des données et des matériaux

Cette étude n'utilise pas de données autres que celles fournies dans le texte.

Abréviations

NP :

Nanoparticule

REAX :

Champ de force réactive

LAMMPS :

Simulateur massivement parallèle atomique/moléculaire à grande échelle

OVITO :

Ouvrir l'outil de visualisation

COR :

Coefficient de restitution