Effet de surface sur le transport du pétrole dans les nanocanaux :une étude de dynamique moléculaire

Contexte

Inspiré par la demande énergétique mondiale sans cesse croissante et la consommation excessive d'énergie conventionnelle, le développement du pétrole de schiste non conventionnel a suscité une grande attention, en raison de ses réserves importantes et de son potentiel de production [1]. L'huile de schiste est l'abréviation de l'huile de schiste biologique mature et l'énergie la plus représentative répertoriée sous les rubriques énergétiques non conventionnelles. Bien que les ressources mondiales connues totales de pétrole de schiste soient plus de trois fois supérieures à celles du pétrole brut conventionnel restant [2], les réserves totales exploitables de pétrole de schiste ont été estimées bien inférieures aux réserves. En outre, le schiste bitumineux est exploité depuis environ 200 ans, mais le développement et l'utilisation du pétrole de schiste sont jusqu'à présent considérablement limités. Tout cela suggère que l'huile de schiste, confinée dans des nanocanaux, est difficile à extraire [3]. La taille du canal des schistes bitumineux varie de 2 à 100 nm de largeur [4, 5], ce qui génère une grande surface spécifique et de nombreux types d'effets de surface. Sous l'influence de l'interaction de surface entre le fluide et le substrat, de nombreux nouveaux phénomènes physiques peuvent être déclenchés, par exemple, l'eau s'écoule beaucoup plus rapidement à l'intérieur des nanotubes que dans un tube macroscopique classique [6, 7], une augmentation anormale de la capacité du carbone au niveau des pores est constatée. tailles inférieures à 1 nm [8], l'affinité de l'eau dans les nanotubes de carbone passe d'hydrophobe à hydrophile lorsque la largeur diminue [9]. Étant situé dans le schiste bitumineux, avec la forte interaction de surface entre les fluides et le substrat de schiste, le fluide présente de nombreux caractères différents de celui du canal macroscopique, tels que la distribution de la densité, la mouillabilité et le coefficient de diffusion [10,11,12], résultant en des propriétés de transport différentes des fluides à travers un tel nanocanal de celles dans un canal à grande échelle. À l'aide de simulations de dynamique moléculaire (MD), Chen et al. ont étudié le comportement de transport de l'eau à l'intérieur d'un nanotube de carbone modèle et ont constaté que la contrainte de cisaillement entre le fluide et le canal était sensible à la taille, et ils ont également vérifié les conclusions de simulation par expérience sur un carbone nanoporeux dans la glycérine [13]. Xue et al. ont considéré le flux de décane dans un nanocanal de silice sous la force motrice de l'inondation de gaz, et ils ont découvert que la pression initiale et l'énergie d'interaction entre l'huile et le substrat jouaient un rôle important dans le déplacement des gouttelettes d'huile [14]. Wang et al. ont simulé le flux d'octane dans des fentes de quartz par des simulations MD, et ils ont constaté que la vitesse s'améliorait avec l'augmentation de la force externe, de la largeur du canal et de la température, et ils ont également constaté que l'effet de surface peut dominer le transport du pétrole dans le nanocanal avec largeur de canal décroissante [15]. Comme mentionné ci-dessus, la forte interaction de surface entre les fluides et le nanocanal a un effet crucial sur l'écoulement du fluide dans le nanocanal. Cependant, il existe peu d'études systématiques sur l'effet des propriétés de surface sur le mécanisme dynamique du transport du pétrole dans les nanocanaux. Comprendre l'influence de l'effet de surface sur le transport de l'huile de schiste dans les nanocanaux est d'une grande importance pour promouvoir le développement et l'utilisation de l'huile de schiste.

Dans ce travail, nous étudions le mécanisme dynamique du transport du pétrole dans les nanocanaux à l'aide de simulations MD et démontrons que l'interaction de surface entre les molécules d'huile et la surface du canal, la rugosité de la surface du canal et l'interaction entre les molécules d'huile ont tous de grands effets sur le centre de masse. (COM) déplacement d'huile dans un nanocanal. La conclusion offrira non seulement un avenir radieux au domaine de l'énergie, mais mettra également en lumière un large éventail de sciences naturelles, telles que l'environnement, la biomédecine, les applications chimiques, énergétiques et industrielles, y compris la translocation de protéines, la séparation membranaire de mélanges et la batterie de canaux. [16,17,18,19,20].

Méthodes

Toutes les simulations MD sont effectuées par le code Discover dans le logiciel Material Studio (Accelrys Inc.). Un potentiel moléculaire optimisé en phase condensée pour les études de simulation atomistique (COMPASS) est utilisé pour décrire les interactions interatomiques. Le champ de force COMPASS est un champ de force général pour tous les atomes basé sur ab initio et paramétré à l'aide de données étendues pour les molécules en phase condensée. Le potentiel de champ de force peut être exprimé comme suit :

Dans l'équation ci-dessus, E _valence fait référence à l'énergie de valence (ou de liaison), qui est généralement représentée par des termes diagonaux tels que l'étirement de la liaison, la flexion de l'angle de valence, la torsion de l'angle dièdre et l'inversion. E _inter-terme fait référence à l'énergie croisée, qui tient compte de facteurs tels que les distorsions de liaison ou d'angle causées par les atomes proches pour reproduire avec précision les propriétés dynamiques des molécules. Et E _{non lié} fait référence à l'énergie non liée, qui représente les interactions entre les atomes non liés et résulte principalement des interactions de van der Waals (vdW) et des interactions électrostatiques. Les trois termes peuvent être représentés par

où b et b ′ sont les longueurs de liaison de deux liaisons adjacentes, et θ , ϕ , et χ sont respectivement l'angle à deux liaisons, l'angle de torsion dièdre et l'angle hors plan. q est la charge atomique, ε est la constante diélectrique, r _ij est le i -j distance de séparation atomique. b ₀ , K _i (i = 2 − 4), θ ₀ , H _i (i = 2 − 4), \( {\phi}_i^0 \) (i = 1 − 3), V _i (i = 1 − 3), \( {F}_{b{ b}^{\prime }} \), \( {b}_0^{\prime } \), \( {F}_{\theta { \theta}^{\prime }} \), \( {\theta}_0^{\prime } \), F _bθ , F _bϕ , \( {F}_{b^{\prime}\theta} \), F _i (i = 1 − 3), F _θϕ , \( {K}_{\phi \theta {\theta}^{\prime }} \), A _ij et B _ij sont ajustés à partir de calculs de mécanique quantique et implémentés dans le module Discover de Materials Studio. Le potentiel de Lennard-Jones est utilisé pour décrire les interactions intermoléculaires entre les molécules d'huile, la molécule d'huile et les nanocanaux [14, 21, 22]. La distance de coupure de 15,5 Å est sélectionnée pour calculer les interactions vdW, et la méthode d'Ewald et la méthode basée sur les atomes sont appliquées pour le calcul des interactions électrostatiques et des interactions vdW, respectivement. Le système est calculé à volume constant et température constante, c'est-à-dire que l'ensemble NVT est utilisé. La température est de 298 K, et la méthode du thermostat Andersen est choisie pour contrôler le système à une température thermodynamique. La condition aux limites périodique est imposée dans les trois dimensions. Les données sont collectées toutes les 5 ps et la trajectoire complète et précise est enregistrée.

Une composition majeure des minéraux rocheux est la silice dans la plupart des formations de schiste [23,24,25]. Ainsi, la surface de silice est sélectionnée comme surface de schiste bitumineux dans notre simulation. Le réseau initial de silice provient de la base de données du logiciel Material Studio. La surface (0 0 1) est clivée, puis une surface rectangulaire est raffinée. Les dimensions de chaque surface de substrat sont de 1,5 × 7 × 0,85 nm ³ . Un canal de séparation le long du z -axe est créé entre les deux surfaces de substrat comme le montre la figure 1a. Les surfaces des canaux sont entièrement modifiées par l'hydroxyle pour représenter les conditions géologiques [26].

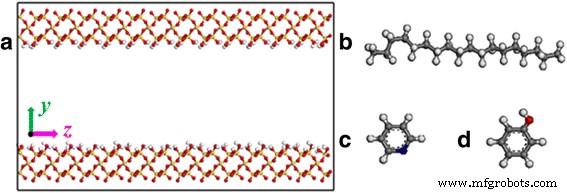
un Représentation du modèle de nanocanaux de silice. Structures moléculaires de b octadécane, c pyridine, et d phénol. Code couleur des atomes :rouge , oxygène; blanc , hydrogène; jaune , silicium; gris , carbone; et bleu , azote

La configuration initiale du système est construite par des molécules d'octadécane s'entassant à l'intérieur du canal de silice. Quarante molécules d'octadécane sont insérées dans le canal fendu d'une largeur de 2 nm, conduisant à une densité de 0,8 g/cm ³ . Nous étudions également les propriétés de transport des molécules de pyridine et de phénol, deux autres composants du pétrole de schiste, pour étudier l'effet des molécules de pétrole sur le transport du pétrole dans les nanocanaux. Les structures de l'octadécane, de la pyridine et du phénol sont extraites de la base de données du logiciel Material Studio, comme le montre la figure 1b–d. Pour garantir une densité de pétrole similaire, le nombre de molécules de pyridine, de molécules de phénol et de molécules d'octadécane dans les canaux d'une largeur de 4 et 6 nm dans nos simulations est de 407, 344, 80 et 120, respectivement.

En utilisant Discover Minimization, nous effectuons d'abord une minimisation d'énergie pour optimiser le système afin que le système soit bien équilibré. Les simulations d'équilibre sont effectuées à l'aide d'une pré-exécution de 500 ps pour s'assurer que le système a atteint un état stable. Ensuite, des simulations de non-équilibre sont effectuées en appliquant une force semblable à la gravité parallèle à la surface du canal (le long du z -axis) à toutes les molécules d'huile afin de favoriser le transport à travers les canaux, ce qui est couramment utilisé dans la simulation du transport de fluides [27,28,29]. Nous notons ici qu'une limitation de la simulation MD est qu'une force comparable à celles des paramètres ambiants est peu pratique, en raison du temps requis pour les calculs MD; ainsi, nous avons appliqué une force qui donne une valeur moyenne de 3.1 × 10 ⁻¹⁴ N sur chaque atome. L'intention de la grande force est d'obtenir des données plus précises pour le transport du pétrole étant donné un temps de simulation fini.

Résultats et discussion

Effet de la largeur du canal

Nous portons d'abord notre attention sur l'effet de la largeur du canal sur les propriétés de transport du pétrole. Sous l'action de la force externe, le nombre d'atomes circulant dans la section transversale du canal augmente progressivement avec le temps de simulation (Fichier supplémentaire 1 :Figure S1, Informations complémentaires). Les molécules d'huile sont tirées pendant environ 2 ns. Comme le montre la figure 2d–f, avec l'incrément de la largeur du canal, la distance de déplacement de l'huile est plus grande après des simulations MD de 2 ns. Pour décrire quantitativement le déplacement du pétrole le long de l'axe du canal, nous calculons le déplacement COM du pétrole entre son emplacement initial et son emplacement final après 2 ns. Simulations MD et sa localisation initiale le long du z -L'axe et le centre de masse sont définis en termes de moyenne pondérée par la masse des coordonnées de l'atome.

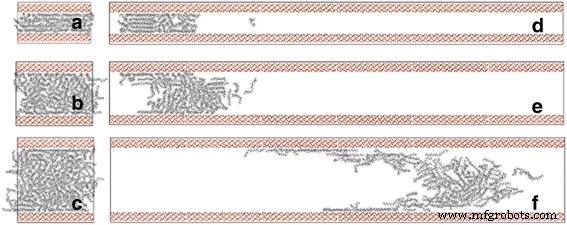
Le modèle initial du processus de transport de molécules d'octadécane entraîné par la force dans des canaux de silice avec des largeurs de a 2, b 4, et c 6 nm, et des instantanés de molécules d'octadécane en d 2, e 4, et f Canaux 6 nm à 2 ns

Dans la Fig. 3, nous présentons le déplacement d'huile après des simulations MD de 2 ns. Les résultats montrent que sous la même force de traction sur chaque atome, le déplacement COM de l'huile dans le canal de 2 nm n'est que de 0,85 nm, ce qui est beaucoup plus petit que celui dans le canal de 6 nm. Cela suggère que le canal le plus étroit fournit une contrainte d'adsorption plus prononcée sur les molécules d'huile.

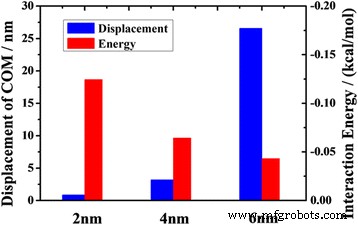
Les déplacements COM du pétrole à 2 ns et les énergies d'interaction moyennes entre le pétrole et le canal en fonction de la largeur du canal

Pour clarifier l'effet de la contrainte d'adsorption, nous calculons l'énergie d'interaction moyenne entre les molécules d'huile et le substrat. L'énergie d'interaction moyenne est calculée comme suit :

où E _{interaction moyenne} est l'énergie moyenne d'interaction entre la molécule d'huile et le substrat ; E _total représente l'énergie totale de l'ensemble du système ; E _huile et E _substrat sont l'énergie des composants du pétrole et des composants du substrat, respectivement ; et N est le nombre total d'atomes des molécules d'huile [14, 30, 31]. La figure 3 montre que le déplacement d'huile diminue avec l'augmentation de l'énergie d'interaction moyenne. Il est évident que l'adsorption entre les molécules d'huile et le canal augmente avec l'énergie d'interaction. La forte adsorption du canal inhibe le transport de l'huile dans le canal étroit. À partir des données illustrées sur la figure 3, nous constatons que lorsque l'énergie d'interaction est augmentée trois fois, le déplacement d'huile diminue de plus de 30 fois. Cela suggère que le transport du pétrole est fortement influencé par l'interaction entre la molécule de pétrole et le substrat. Cependant, cet effet diminue avec l'augmentation de la largeur du canal. L'effet de taille sur le transport du pétrole est plus évident dans les nanocanaux que dans les microcanaux (Fichier supplémentaire 1 :Figure S2). Par conséquent, la réduction de l'énergie d'interaction entre la molécule d'huile et le substrat est un facteur clé pour améliorer le transport du pétrole dans les nanocanaux.

On peut voir sur la figure 2 qu'il y a eu des structures en couches évidentes près de la surface du nanocanal, avec une épaisseur d'environ 5 Â. Il convient de noter que la couche en contact avec la surface du canal et la couche au centre du canal sont appelées respectivement couche de contact et couche centrale. De toute évidence, des couches de molécules d'huile bien ordonnées se trouvent dans la région proche de la surface. L'orientation des molécules d'octadécane est communément caractérisée par l'angle θ entre le vecteur normal à la surface du canal et certains vecteurs qui sont formés par la ligne reliant les deux atomes de carbone à l'extrémité d'une molécule d'octadécane [15, 29]. La distribution d'orientation des molécules d'octadécane dans chaque couche à 2 ns est présentée sur la figure 4. Ici, θ = 80 ^o ∼ 90 ^o correspond à l'orientation parallèle de la molécule, alors qu'une valeur de θ = 0 ^o ∼ 10 ^o signifie que la molécule est perpendiculaire à la surface du canal. On peut voir que les molécules d'octadécane sont principalement parallèles à la surface dans les couches de canal de 2 nm et dans la couche de contact de canal de 4 nm et de canal de 6 nm, en raison de la forte interaction huile-surface (Fig. 5b). Pour les couches centrales du canal de 4 nm et du canal de 6 nm, il n'y a pas d'orientation préférentielle des molécules d'octadécane, ce qui signifie que ces molécules d'octadécane ont tendance à se trouver à divers angles par rapport à la surface du canal. Les molécules d'octadécane alignées dans la couche de contact peuvent être importantes pour les propriétés de transport des molécules d'huile dans les nanocanaux.

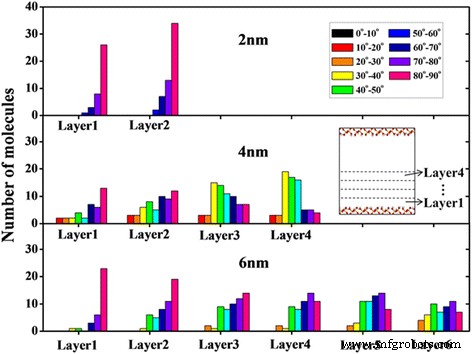
La distribution de l'angle d'orientation des molécules d'octadécane dans chaque couche pour différentes largeurs de canal

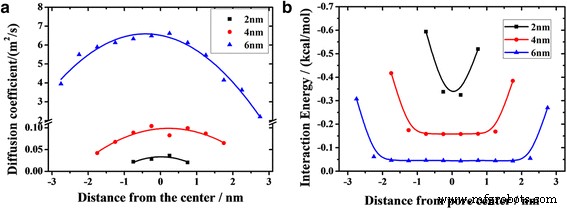
un Profils de coefficient de diffusion de l'huile dans des canaux de largeur différente. b Dépendance à distance de l'énergie d'interaction moyenne entre les molécules d'huile et la silice (avec symboles). Les lignes pleines représentent les fonctions d'ajustement

Ensuite, nous observons que les temps de démarrage (définis comme le moment où le déplacement d'une couche est supérieur à 5 Å) pour différentes couches sont différents en vérifiant les trajectoires. Les données de temps de démarrage répertoriées dans les informations complémentaires (Fichier supplémentaire 1 :Tableau S1) montrent que le temps de démarrage de la couche de contact augmente avec la diminution de la largeur du canal, ce qui signifie que la force de traction nécessaire pour démarrer le déplacement d'une couche de contact dans un canal plus étroit est plus grand que celui requis dans un canal plus large. De plus, le temps de démarrage de la couche centrale est beaucoup plus tôt que celui de la couche de contact.

De plus, nous constatons que le débit d'huile diminue avec l'augmentation de la distance par rapport à l'axe du canal, et le débit de la couche de contact diminue avec la diminution de la largeur du canal (Fig. 2d-f). Pour décrire quantitativement ces caractères, nous étudions le coefficient de diffusion des molécules d'huile à un endroit différent du centre du canal, qui est obtenu à partir de l'évolution temporelle du déplacement quadratique moyen selon

où r _i désigne le vecteur position de i particule, et les parenthèses angulaires indiquent une moyenne d'ensemble. La figure 5a montre comment les coefficients de diffusion des couches dépendent de la position dans le nanocanal. Les courbes du canal 4 nm et du canal 6 nm présentent un style parabolique, c'est-à-dire que vers la surface du canal, les coefficients de diffusion des couches diminuent progressivement. Le canal 6 nm montre la plus grande différence entre la valeur haute et la valeur basse de 4,4 m ² /s, tandis que le canal de 2 nm détient la différence minimale de 0,016 m ² /s. Les coefficients de diffusion des couches dans le canal de 2 nm sont légèrement différents, de sorte que la surface avant de l'huile ressemble à un piston. En outre, nous constatons que les coefficients de diffusion des couches à la même distance de la surface du canal sont assez différents pour différents canaux (Fig. 5a). Par exemple, le coefficient de diffusion de la couche en contact avec la surface inférieure du canal dans un canal de 6 nm est de 3,9 m ² /s, alors que dans le canal 2 nm n'est que de 0,02 m ² /s. Cela signifie que le débit des couches à la même distance de la surface du canal augmente avec l'augmentation de la largeur du canal.

Sur la figure 5b, nous présentons l'énergie d'interaction moyenne entre les molécules d'huile à différents endroits du centre du canal et du canal. Les énergies d'interaction sont évidemment plus grandes aux deux extrémités des courbes et diminuent rapidement à moins de 1 nm car le substrat a une forte adsorption sur les molécules d'huile de l'ordre de 1 nm, et c'est l'une des raisons du démarrage lent des couches de contact. Cependant, les énergies d'interaction entre les molécules d'huile et le canal ne peuvent pas expliquer de manière adéquate la forme de la surface avant, car ses valeurs pour les couches en dehors de la plage de forte adsorption sont presque les mêmes. La surface avant de la parabole n'est pas seulement liée à l'interaction entre l'huile et le canal, mais aussi à l'interaction entre les molécules d'huile. L'interaction intermoléculaire contribue à la viscosité du fluide, qui joue un rôle important dans le transfert de quantité de mouvement dans le fluide viscoélastique. Étant donné que la plage d'adsorption du canal sur le pétrole est d'environ 1 nm, certaines couches sont situées dans la zone, comme indiqué par l'ombre sur la figure 6. Les fortes interactions superficielles entre le pétrole et le substrat bloquent le transport des couches de pétrole dans l'ombre. L'élan est transféré des calques hors de l'ombre aux calques dans l'ombre. Le nombre d'atomes hors de l'ombre diminue avec la diminution de la largeur du canal. Ainsi, moins d'impulsion est transférée aux couches dans l'ombre dans un canal plus étroit. Ainsi, la vitesse de diffusion de la couche de contact diminue avec la diminution de la largeur du canal.

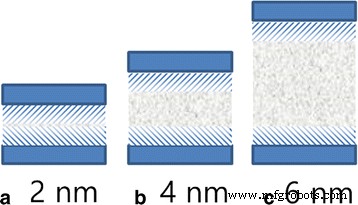
un , b , c Schéma de la plage d'adsorption entre l'huile et le substrat

Effet de la polarité

Le pétrole de schiste contient toujours les composants du pétrole polaire, et ces composants du pétrole polaire jouent un rôle important dans l'adsorption de l'interface pétrole/silice [21, 32], il est donc crucial de comprendre leur impact sur le transport du pétrole. Avec le phénol et la pyridine par exemple, nous effectuons des simulations dans un canal de 4 nm, et les nombres d'atomes de phénol et de pyridine sont approximativement égaux au nombre d'atomes d'octadécane dans un canal de 4 nm. Les instantanés de la pyridine, du phénol et de l'octadécane dans le canal de silice à 2 ns sont présentés sur la figure 7. Par rapport aux molécules d'octadécane, les molécules de phénol et les molécules de pyridine ne peuvent presque pas être entraînées par la force de traction. La ligne brisée de la figure 8 montre les déplacements COM de différentes molécules d'huile après des simulations MD de 2 ns. Bien que les forces de traction sur chaque atome soient égales, le déplacement COM de l'octadécane est presque 16 fois plus important que le déplacement COM du phénol et de la pyridine.

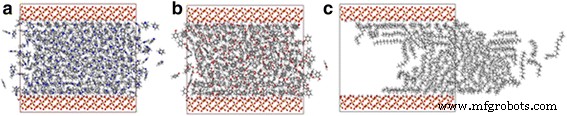
Instantanés de a pyridine, b phénol, et c transport d'octadécane dans des canaux de silice de 4 nm à 2 ns

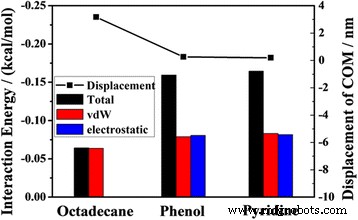
Les déplacements COM de l'huile à 2 ns et les énergies moyennes d'interaction (totale, vdW et électrostatique) entre les différents composants et le canal

Afin de comprendre ces résultats, nous calculons l'énergie de l'interaction totale, de l'interaction vdW et de l'interaction électrostatique entre les différents composants et le canal. L'histogramme de la figure 8 illustre que l'énergie d'interaction totale entre le phénol (pyridine) et le substrat de silice est plus grande que celle entre l'octadécane et le canal de silice. Étant donné que la molécule d'octadécane est une molécule à chaîne non polaire, l'interaction totale entre les molécules d'octadécane et le canal résulte principalement de l'interaction vdW, et il y a peu d'interaction électrostatique, tandis que les contributions de l'interaction vdW et de l'interaction électrostatique entre le phénol (pyridine) et le canal à l'interaction totale sont presque les mêmes.

Pour étudier l'influence de la polarité sur le transport du pétrole, nous calculons la quantité de mouvement dipolaire des trois molécules en utilisant la simulation du premier principe. Les détails de la performance suivent nos travaux antérieurs [33,34,35,36]. Les résultats montrent que les moments dipolaires de l'octadécane, du phénol et de la pyridine sont respectivement de 0,0322, 1,3059 et 2,2449 Debye. Cela indique que les molécules d'huile polaires sont beaucoup plus difficiles à conduire que les molécules non polaires dans les nanocanaux. Mais le déplacement COM de l'huile n'augmente pas toujours avec une polarité décroissante. Pour les deux molécules d'huile polaires, la polarité du phénol est plus faible que la polarité de la pyridine, mais leurs déplacements COM sont presque égaux.

Effet des types de matériaux

Les caractéristiques de transport des molécules d'huile sont également comparées parmi ces nanocanaux fabriqués à partir de divers types de matériaux, notamment la silice, l'or et la calcite. La figure 9 montre les instantanés des molécules d'octadécane dans les canaux de calcite et d'or à 2 ns. La figure 9a montre un transport distinct des molécules d'huile dans le canal de calcite, indiquant que les molécules d'octadécane dans la calcite peuvent également être entraînées par la force de traction, tandis que les molécules dans le canal d'or peuvent à peine se déplacer (Fig. 9b).

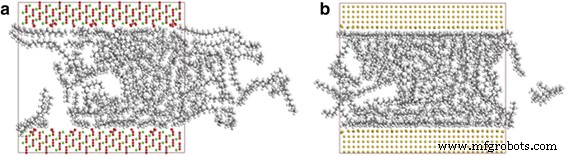
Instantanés du transport de l'octadécane en 4 nm a canal de calcite et b canal d'or à 2 ns. Code couleur des atomes :vert, calcium; jaune, or

La figure 10 montre les déplacements COM des molécules d'octadécane dans les canaux de divers matériaux et les énergies d'interaction moyennes entre le pétrole et les différents canaux de matériaux. Le déplacement COM du pétrole dans le canal de silice est beaucoup plus important que celui dans le canal d'or. Le phénomène peut s'expliquer par l'effet de l'interaction entre les molécules d'huile et le canal. L'interaction moyenne est beaucoup plus faible entre les molécules d'huile et le canal de silice qu'entre les molécules d'huile et le canal d'or. Mais pour le transport des molécules d'huile dans le canal de silice et dans le canal de calcite, ce facteur ne peut pas expliquer adéquatement la différence. L'énergie moyenne d'interaction entre les molécules d'huile et le canal de silice ne semble pas très différente de celle entre les molécules d'huile et le canal de calcite, mais les déplacements COM dans les deux cas sont assez différents. La raison peut être corrélée aux atomes de surface et à la texture de la surface. Ces résultats indiquent que le transport du pétrole est fortement influencé par l'interaction entre les molécules de pétrole et le canal, mais lorsque les valeurs de l'énergie d'interaction sont similaires, le transport du pétrole dans le nanocanal est la compétition entre ces facteurs.

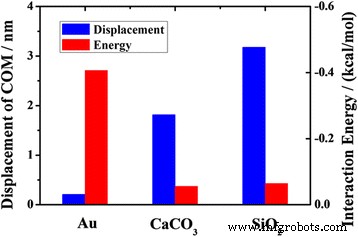
Les déplacements COM de l'huile à 2 ns et les énergies d'interaction moyennes entre l'huile et les substrats de différents matériaux

Effet de la rugosité de surface

Comme cela est bien connu, la rugosité de surface de taille nanométrique a peu d'influence sur les écoulements de fluide à l'intérieur de canaux de taille microscopique. Cependant, il a été démontré que la rugosité de surface de taille nanométrique a une grande influence sur le transport des fluides dans les nanocanaux [37,38,39]. Pour étudier l'effet de la rugosité sur le transport de l'octadécane, nous construisons des surfaces rugueuses en découpant une petite quantité d'atomes de la surface du substrat, de sorte qu'une cavité d'une profondeur de d =3 (ou 6 ) et une largeur de 35 est formée sur la surface du substrat. Les atomes d'oxygène nus ont été modifiés par des atomes d'hydrogène. Five and ten octadecane molecules are added to 3 Å cavity and 6 Å cavity, respectively, and the external force is increased correspondingly. Figure 11 shows the comparison of snapshots for octadecane flowing through rough channel with cavity depths of 3 and 6 Å at 2 ns. We observe that inside every cavity, there are some oil molecules, and their localizations are affected by the cavity, which results in a reduction of velocity values inside the cavity, as well as the velocity of oil molecules nearby. And this becomes more obvious when d  = 6 Å, as shown in Fig. 11b. To quantify the influence of roughness on transportation, we further calculate the COM displacement of oil in rough channels. The COM displacements of oil in channels with 3 and 6 Å depth cavity are 3.95 and 3.07 Å, respectively. When d  = 6 Å, the value of oil displacement is 3.07 Å, which is smaller than the value 3.17 Å of oil molecules in flat channel. Somewhat surprisingly, however, for d  = 3 Å, the displacement is even larger than that in flat channel. We expect that these characters are contributed by two parts:(1) the cavity increases the width of the nanochannel so that the oil molecules have a greater diffusion coefficient according to the above discussion, which facilitates the transportation of oil; (2) the oil molecules in cavity can suppress the transportation of oil molecules nearby and therefore decrease the oil transportation speed. For the oil molecules in channel with d  = 3 Å, the effect of suppression caused by the less oil molecules in cavity is less than the effect of facilitation caused by the width increment. When d  = 6 Å, the diffusion coefficient of oil molecules is further increased; however, more oil molecules are suppressed by the deeper cavity, and the effect of suppression on the transportation of oil molecules is more than that of facilitation, thereby reducing the oil displacement. Because of these complications, we cannot separate these parts and judge how much contribution of each part has on the displacement.

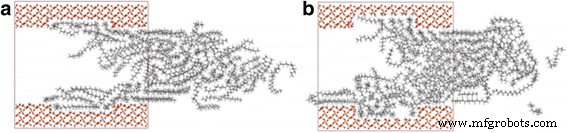
Snapshots of octadecane transportation in rough channel with the cavity depth of a 3 and b 6 Å at 2 ns

Conclusions

In this study, we investigate the mechanism of oil transportation in nanochannels using molecular dynamics simulations. It is demonstrated that the oil displacement in a 6 nm channel is over 30 times larger than that in a 2 nm channel, and the diffusion coefficient of oil molecules at the center of the 6 nm channel is almost two times more than that near the channel surface, due to interaction difference between the oil molecules and channels. Besides, we find that both the polarity of oil molecules and channel component have great effects on the interaction between oil molecules and channel in the channels with same width; the larger the interaction between oil molecules and channel is, the smaller the oil displacement is. Finally, we demonstrate that surface roughness can obviously affect oil transportation in nanochannels. The mechanism by which the cavity structure affects the transportation of oil is an intricate issue, which should be further studied. Our findings would contribute to revealing the mechanism of oil transportation in nanochannels and therefore are very important for design of oil extraction in nanochannels.

Abréviations

COM:

Center of mass

COMPASS:

Condensed-phase optimized molecular potential for atomistic simulation studies

MD :

Molecular dynamics

vdW:

van der Waals