Modélisation et simulation de dynamique moléculaire de la coupe de diamant de cérium

Contexte

Le cérium (Ce) avec un numéro atomique de 58 est l'un des métaux lanthanides les plus abondants. Le cérium a de nombreuses applications pour ses propriétés mécaniques, physiques et chimiques fascinantes. Il est connu que la morphologie de la surface usinée des pièces métalliques a une forte influence sur leur fonctionnalité, leurs performances et leur cycle de vie. Par exemple, la résistance à la corrosion des pièces métalliques peut être efficacement améliorée en réduisant la rugosité de surface ou en introduisant une contrainte résiduelle de compression dans la surface usinée [1,2,3]. Plus récemment, Yan et al. ont utilisé une nouvelle technique d'usinage mécanique basée sur la pointe pour fabriquer des microcavités triangulaires périodiques sur Cu(111), qui s'est avéré être un substrat de diffusion Raman amélioré en surface [4]. Spécifiquement pour le cérium utilisé pour stocker l'hydrogène [5], l'état de surface du cérium influence fortement la réaction entre le cérium et l'hydrogène à température ambiante. Par conséquent, l'obtention d'une grande précision de la morphologie de la surface usinée du cérium est cruciale pour ses applications. La coupe au diamant ultra-précise est une technique de fabrication importante pour obtenir une finition de surface ultra-lisse avec une intégrité de surface élevée, une rugosité de surface ultra-faible, une planéité élevée, une faible évolution de la structure métallographique et de faibles dommages sous la surface [6, 7]. Cependant, des travaux expérimentaux ou théoriques sur la taille du cérium au diamant avaient rarement été rapportés. De plus, étant donné que dans le processus de coupe au diamant ultra-précis, le rayon d'arête de l'outil est comparable à la profondeur de coupe, les propriétés du matériau de la pièce jouent un rôle important, voire dominant, dans le processus de coupe. Par conséquent, la compréhension des mécanismes d'usinage du cérium est difficile pour son comportement de déformation complexe.

Premièrement, le cérium est connu pour son diagramme de phase pression-température extraordinairement riche entraîné par la délocalisation des électrons 4f. À la pression atmosphérique et aux basses températures inférieures à 110 K, le -Ce (cubique à faces centrées (fcc)) est stable. À des températures élevées allant de 45 à 275 K, le -Ce se transforme en β-Ce (double hexagone compact (dhcp)). Le -Ce (fcc) est stable à des températures modérées entre 270 et 999 K. À des températures élevées entre 999 K et la température de fusion de 1071 K, le δ-Ce (cubique centré (bcc)) est stable [8,9 ,10,11]. En particulier, la transformation de phase isostructurale la plus fascinante du -Ce trivalent de faible densité au α-Ce beaucoup plus dense à 295 K et sous 8 kbar s'accompagne d'un effondrement volumique important de 20 % [8, 12, 13, 14 ]. La modification induite par la transformation de phase de la structure électronique et de la configuration de liaison dans le cérium a inévitablement un fort impact sur son comportement à la déformation. Spécifiquement, la température élevée et la pression élevée formées dans la région de contact entre l'outil de coupe et la pièce à usiner peuvent entraîner une transformation de phase du cérium dans le processus de coupe du diamant. Deuxièmement, le cérium métallique a une ductilité considérable régie par les dislocations [15]. Il est connu que la nucléation et le glissement des dislocations jouent un rôle clé dans la déformation plastique des métaux fcc sous usinage mécanique. Cependant, l'interaction entre les transformations de phase et les dislocations dans la coupe diamantée du cérium est encore largement méconnue.

Les constituants des mécanismes d'usinage consistent en un comportement de déformation microscopique du matériau de la pièce et sa corrélation avec les résultats d'usinage macroscopiques en termes de force de coupe, de profil de copeaux et de morphologie de la surface usinée. En tant que complément important aux expériences d'usinage, la simulation de la dynamique moléculaire (MD) s'est avérée être un outil puissant pour élucider les mécanismes d'usinage mécaniques fondamentaux de différents types de matériaux. Li et al. ont rapporté que la profondeur d'usure minimale du Cu(111) monocristallin sous nanograttage qui équivaut à la profondeur de pénétration critique à laquelle la plasticité s'initie augmente avec le rayon de la sonde [16]. Plus récemment, ils ont étudié les comportements mécaniques et les mécanismes de déformation des alliages à haute entropie AlCrCuFe sous nanograttage et ont rapporté un volume d'empilement de surface plus important que les métaux purs en raison de sa bonne stabilité à haute température du matériau d'alliage [17]. Gao et al. ont étudié la génération et l'évolution de la plasticité et des défauts dans la coupe orthogonale d'un Bcc Fe [18]. Zhu et al. ont rapporté un effet de taille sur la dépendance de la forme de la sonde du nanoscratching [19]. Hosseini et al. ont étudié les effets du rayon d'arête de l'outil sur le nano-usinage du cuivre monocristallin [20]. Liu et al. ont constaté que la différence entre les coefficients de frottement statique et dynamique disparaît dans le frottement d'aspérité unique de Cu (111) en raison de l'interférence entre les aspérités [21]. Romero et al. ont trouvé que l'adhérence lors de la coupe orthogonale d'un substrat de cuivre peut être renforcée en faisant varier l'angle de coupe de l'outil et en choisissant des orientations de réseau spécifiques [22]. Yang et al. ont indiqué que la vitesse et la direction d'auto-rotation abrasive ont une influence significative sur la morphologie et la qualité de la surface usinée du cuivre monocristallin sous polissage [23]. Vargonen et al. ont rapporté que la perte de hauteur de pointe par distance de grattage pendant le grattage est fonction de la contrainte normale et de l'angle d'effilage de la pointe [24]. Sun et al. impact avéré du GB sur le grattage du cuivre bicristallin [25]. Chen et al. ont constaté que les molécules d'eau réduisent efficacement le frottement entre l'outil et la pièce dans la coupe nanométrique du cuivre [26]. Wu et al. ont rapporté que l'énergie de liaison a une influence significative sur le frottement [27]. De plus, par rapport aux investigations expérimentales, les propriétés mécaniques de chaque phase de cérium peuvent être étudiées de manière pratique au moyen de simulations MD, ce qui est crucial pour comprendre l'interaction entre les transformations de phase et les dislocations dans le cérium. Plus récemment, Zhang et al. ont étudié les interactions entre la transformation de phase et la dislocation à la transition élastique-plastique dans la nanoindentation du silicium par des simulations MD [28]. Cependant, à notre connaissance, il n'y a pas de travaux rapportés sur l'investigation MD de l'usinage mécanique du cérium.

Par conséquent, dans le présent travail, nous établissons d'abord le modèle MD de la coupe au diamant du cérium en construisant des configurations atomiques de la pièce et de l'outil, en attribuant des potentiels empiriques pour les interactions atomiques Ce-Ce et Ce-C, et en caractérisant deux phases fcc du cérium. Avec le modèle MD établi, nous effectuons ensuite des simulations MD de la coupe au diamant du cérium pour élucider les mécanismes d'usinage fondamentaux du cérium et étudier les influences de l'angle de coupe de l'outil de coupe et de l'orientation cristallographique de la pièce sur le processus de coupe.

Méthodes

Modèle MD de taille de diamant

La figure 1 montre le modèle MD de coupe au diamant, qui se compose d'une pièce de cérium monocristallin et d'un outil de coupe au diamant. La pièce en cérium a une dimension de 41, 25 et 31 nm dans les directions horizontale, verticale et longitudinale, respectivement, et se compose d'un million d'atomes γ-Ce dans la structure fcc. La condition aux limites périodique n'est appliquée que dans le sens longitudinal. La pièce se compose de deux types d'atomes, respectivement les atomes inférieurs et les atomes mobiles. La couche d'atomes du bas d'une épaisseur de 2 nm est fixée dans l'espace pour empêcher tout mouvement rigide de la pièce. Le mouvement des atomes mobiles suit l'équation du mouvement de Newton avec un algorithme d'intégration vitesse-verlet. La température de chaque atome de la pièce est surveillée pendant le processus de coupe pour représenter la dissipation de chaleur générée. Pour traiter l'influence de l'orientation cristallographique, trois pièces de cérium avec (010), (110) et (111) surface libre dans la direction verticale sont considérées. L'outil de coupe en diamant avec une arête vive a un angle de relief de 9° et est composé de 0,1 million d'atomes de C dans la structure du diamant. Sept angles d'inclinaison, tels que -30°, -20°, -10°, 0°, 10°, 20° et 30°, sont utilisés pour traiter l'influence de l'angle d'inclinaison. Compte tenu de la dureté ultra élevée du diamant par rapport au cérium et de la distance de coupe ultra-courte, l'usure de l'outil diamanté pendant le processus de coupe n'est pas prise en compte. Par conséquent, l'outil de coupe en diamant est défini comme un corps rigide, c'est-à-dire que les coordonnées et les vitesses de tous les atomes de l'outil de coupe sont mises à jour à chaque pas de temps, de sorte que l'outil de coupe se déplace comme une seule entité sans aucune déformation.

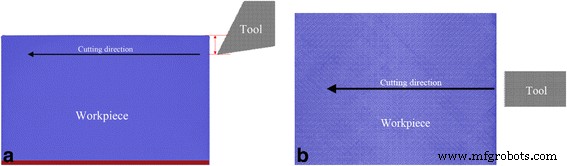
Modèle MD de taille de diamant de cérium; (couleur en ligne) Modèle MD de taille de diamant de cérium. un Vue de face et b vue de dessus . Rouge et couleurs bleues représentent les atomes de Ce inférieurs et mobiles, et la couleur grise indique les atomes C

Il existe trois types d'interactions atomiques dans le système simulé, comme Ce-Ce dans la pièce en cérium, Ce-C entre la pièce en cérium et l'outil de coupe en diamant, et C-C dans l'outil de coupe en diamant, respectivement. Les interactions C-C sont omises car l'outil de coupe diamanté est traité comme un corps rigide sans aucune déformation dans le processus de coupe. La méthode de l'atome intégré (EAM) composée d'un potentiel de paire d'interactions et d'une énergie d'intégration d'électrons a été largement utilisée pour décrire des systèmes métalliques, qui peuvent être exprimés sous la forme

où r _ij est la distance entre les atomes i et j , ϕ _ij est le potentiel de paire entre les atomes i et j , F _i représente l'énergie d'intégration qui est générée lorsqu'un atome i est intégré, ρ _i est la densité électronique à i atome généré par tous les atomes sauf l'atome i , et ρ _j est une fonction de la densité électronique de l'atome j à l'atome i . Les paramètres EAM pour le cérium par Sheng et al. sont utilisés pour décrire les interactions Ce-Ce, qui sont capables de décrire avec précision les propriétés élastiques en vrac des phases de cérium fcc [29]. Le potentiel Morse est utilisé pour décrire l'interaction Ce-C, qui peut être exprimée comme

où D ₀ (0,087 eV) est l'énergie de cohésion, (5.14) est le module d'élasticité et r ₀ (2,93 Å) représente la distance d'équilibre entre les atomes i et j , respectivement. Le rayon de coupure du potentiel Morse est choisi à 1,0 nm [30].

Le système de simulation tel que créé est d'abord équilibré à sa configuration d'équilibre à 30 K et sous 0 bar dans l'ensemble NPT (nombre constant d'atomes N , pression constante P , et température constante T ). Ensuite, la pièce équilibrée est soumise à la coupe au diamant avec une vitesse constante de 100 m/s et une profondeur de coupe de 4 nm dans l'ensemble canonique (nombre constant d'atomes N , volume constant V , et température constante T ). Le sens de coupe est indiqué par des flèches colorées en rouge dans différents points de vue du modèle de coupe. Et la force de coupe est définie comme la composante de force le long de la direction de coupe. La profondeur de coupe utilisée dans l'expérience d'usinage ultra-précis est de quelques micromètres. Nous notons que la dimension simulée de la pièce et la profondeur de coupe sont de plusieurs ordres de grandeur plus petites que celles utilisées dans les expériences de coupe au diamant ultra-précise, en raison de la limitation de l'échelle de longueur dans les simulations atomistiques. Nous notons également que la vitesse de coupe employée de 100 m/s dans les simulations MD actuelles de coupe nanométrique est de plusieurs ordres de grandeur plus élevée que les vitesses typiques de dizaines de micromètres par seconde utilisées dans les expériences de coupe de diamant ultra-précise, donnant l'exigence intrinsèque de la le pas de temps d'intégration doit être de l'ordre de la femtoseconde (fs). L'analyse de voisinage commun (CNA) est utilisée pour identifier les types de défauts de réseau [31], et le schéma de coloration est le suivant :le vert représente les atomes fcc, le rouge pour les atomes hexagonaux compacts (hcp), le bleu pour les atomes cubiques centrés sur le corps. (bcc) et gris pour les autres atomes, y compris les atomes de surface et les noyaux de dislocation. Toutes les simulations MD sont effectuées en utilisant le code LAMMPS avec un pas de temps d'intégration de 1 fs [32]. Et l'OVITO est utilisé pour visualiser les données MD et générer des instantanés MD [33].

Caractérisation des phases de cérium

Dans le présent travail, cinq phases de cérium sont considérées, respectivement γ, α, , et . Le tableau 1 répertorie les paramètres structurels et les conditions de température-pression pour chaque phase qui sont collectées à partir de la littérature [8,9,10,11]. La configuration atomique en vrac de chaque phase est ensuite construite conformément au tableau 1. Ensuite, des simulations informatiques de la tension uniaxiale, du cisaillement et de la compression uniforme des configurations en vrac telles que construites sont effectuées pour dériver les propriétés mécaniques des différentes phases Ce. En raison de la température stable élevée proche du point de fusion du cérium, les propriétés mécaniques du -Ce ne sont pas calculées car il est difficile d'effectuer des tests mécaniques sur la phase liquide. Le tableau 2 répertorie les constantes élastiques dérivées et les propriétés mécaniques de chaque phase de cérium. Le module de Young calculé de la phase γ-Ce monocristalline est de 24,17 GPa, ce qui est comparable à la valeur expérimentale de 36,7 GPa rapportée dans la nanoindentation de son homologue polycristallin [10]. De plus, les valeurs calculées de C44 et 1/2(c11-c12) diffèrent d'un facteur 3, ce qui est bien en accord avec la valeur expérimentale en utilisant des techniques de diffusion inélastique de neutrons [34]. Le tableau 2 démontre que le α-Ce plus dense a des propriétés mécaniques considérablement améliorées par rapport à sa phase γ-Ce de faible densité isostructurale.

La fonction de distribution radiale (RDF), définie comme les variations de densité dans un système de particules avec la distance d'une particule de référence sous la forme de pics aigus. Le RDF peut être déduit des spectres des rayons X et des données de diffraction des neutrons [35, 36]. Par conséquent, c'est l'un des outils les plus importants pour la caractérisation structurelle des liquides et des solides et agit comme un lien important entre les arrangements atomiques microscopiques et les propriétés macroscopiques. Dans l'étude actuelle, le RDF est utilisé pour caractériser les différences structurelles entre les différentes phases de cérium. La figure 2a trace les histogrammes RDF pour les cinq phases de cérium, dans lesquelles les pics représentent les caractéristiques de la structure de réseau correspondante :la première, la deuxième et la troisième distance du voisin le plus proche du -Ce sont de 3,64, 5,13 et 6,3 Å, respectivement ; la première, la deuxième et la troisième distance du voisin le plus proche du -Ce sont respectivement de 3,41, 4,85 et 5,92 Å ; la distance du premier et du deuxième voisin le plus proche du -Ce est respectivement de 3,53 et 6,75 Å ; la première, la deuxième, la troisième et la quatrième distance du voisin le plus proche du -Ce sont respectivement de 2,96, 3,33, 4,91 et 5,69 Å ; la première, la deuxième, la troisième et la quatrième distance du voisin le plus proche du -Ce sont respectivement de 3,71, 3,97, 5,27 et 5,92 Å. Pour démontrer la faisabilité de prédire les transformations de phase entre deux phases de cérium fcc par les paramètres de potentiel EAM employés, la compression uniforme du γ-Ce en vrac jusqu'à atteindre un effondrement de volume de 20 % est effectuée. La figure 2b présente le RDF avant et après la compression, qui coïncide respectivement bien avec le RDF du -Ce et du α-Ce, indiquant l'occurrence de la transformation de phase γ ➔ α la plus connue [12,13,14] .

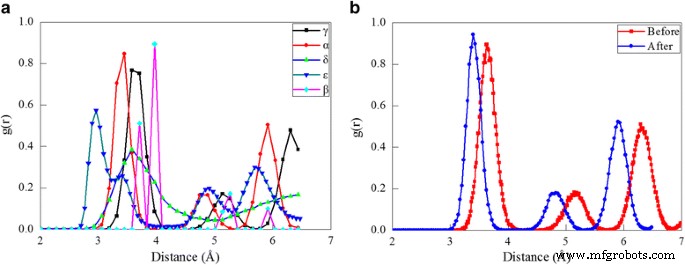
Analyse RDF des phases de cérium ; (couleur en ligne) a RDF des phases de cérium. b RDF avant et après la compression du γ-Ce

Résultats et discussion

Mécanismes d'usinage du cérium

Une simulation MD de la coupe au diamant de Ce(010) est d'abord réalisée pour élucider les mécanismes fondamentaux d'usinage du cérium. L'outil de coupe diamant utilisé a un angle de coupe de 0°. Il y a trois composantes de la force d'usinage, comme la force de coupe le long de la direction horizontale, la force normale perpendiculaire à la surface usinée et la force latérale le long de la direction longitudinale, respectivement. La figure 3 montre les variations de la force de coupe et de la force normale avec la longueur de coupe pendant le processus de coupe, qui sont classées en trois zones selon la longueur de coupe. En conséquence, la sous-figure dans chaque zone montre une configuration de coupe représentative, dans laquelle les atomes sont colorés en fonction de leurs valeurs CNA, et les atomes fcc ne sont pas affichés pour une visualisation claire des défauts.

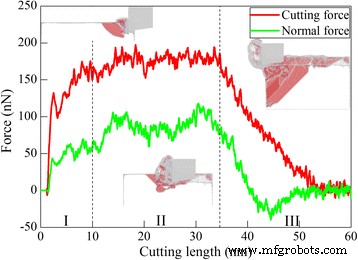
Variation de la force d'usinage ; (couleur en ligne) variation de la force de coupe et de la force normale avec la longueur de coupe lors de la coupe au diamant de Ce(010) sous un angle de coupe de 0°. Les sous-figures présentent des configurations de défauts représentatives dans différentes zones, dans lesquelles les atomes sont colorés en fonction de leurs valeurs CNA

On voit sur la figure 3 que la force de coupe et la force normale ont toutes deux des valeurs négatives lorsque l'outil de coupe est juste à côté de la pièce, en raison de l'adhérence entre l'outil de coupe et la pièce. Lorsque l'outil de coupe commence à entrer en contact avec la pièce, le matériau subit d'abord une déformation élastique, accompagnée d'augmentations rapides à la fois de la force de coupe et de la force normale. La figure 3 montre que la force de coupe et la force normale chutent rapidement à une longueur de coupe de 2,3 nm, indiquant le début de la déformation plastique. Lors d'une nouvelle coupe, la force de coupe et la force normale augmentent avec de fortes fluctuations causées par des événements de nucléation successifs. On voit sur la sous-figure de la zone II qu'il y a une dislocation partielle de Shockley 1/6<112> considérable générée au voisinage de la zone de coupe. La force de coupe et la force normale fluctuent principalement autour de valeurs constantes dans la longueur de coupe allant de 10 à 35 nm, indiquant que le processus de coupe est stable. Et les dislocations dans la zone II résident principalement à la fois devant et sous l'outil de coupe diamanté. Lorsque la longueur de coupe atteint 35 nm, l'outil de coupe commence à se séparer de la pièce, accompagné d'une diminution significative de la force de coupe et de la force normale. La sous-figure de la zone III montre qu'il y a des dislocations considérables bloquées par le côté gauche de la pièce. La force de coupe et la force normale deviennent stables jusqu'à ce que le copeau formé soit complètement séparé de la pièce. La figure 3 montre que pendant le processus de coupe, la force normale est inférieure à la force de coupe.

La figure 4a–d présente les structures de défauts instantanés dans la pièce à différentes longueurs de coupe. Les atomes sont colorés en fonction de leurs valeurs CNA et les atomes fcc ne sont pas affichés. En conséquence, la figure 4e–h présente des morphologies de surface usinées colorées par leurs hauteurs atomiques. L'inspection dynamique de l'évolution des défauts montre que la plastification de la pièce s'accompagne de la nucléation de 1/6<112> luxations partielles de Shockley de la surface libre du côté droit et de leur glissement ultérieur sur des plans de glissement {111} adjacents et le long de <110> directions de glissement. Le mouvement des dislocations partielles de Shockley s'accompagne d'une expansion des failles d'empilement délimitées par des noyaux de dislocation. Avec la progression du processus de coupe, une grande quantité de dislocations partielles est émise depuis la surface libre supérieure devant l'outil de coupe, ce qui entraîne des copeaux considérables formés le long de la face de coupe de l'outil de coupe, comme le montre la figure 4f. Simultanément, les dislocations derrière l'outil de coupe se déplacent vers le haut pour s'annihiler à la surface libre supérieure, conduisant à une récupération significative de la surface usinée. La figure 4c montre que lorsque l'outil de coupe s'approche de la limite gauche de la pièce, la propagation des dislocations est fortement bloquée par la surface libre du côté gauche, accompagnée d'un volume de copeaux considérablement accru, comme le montre la figure 4g. La figure 4d montre qu'après la séparation complète entre la puce et la pièce, la densité de dislocation dans la pièce diminue considérablement en raison de l'annihilation de la dislocation sur la surface libre supérieure.

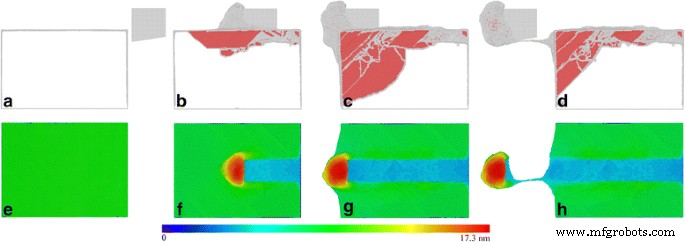
Structures de défauts et morphologies de surfaces usinées ; (couleur en ligne) Instantanés MD des structures de défauts instantanées (rangée du haut ) et la morphologie des surfaces usinées (rang du bas ) dans la coupe diamantée de Ce(010) sous un angle de coupe de 0°. Longueurs de coupe :a , e 0,0 nm, b , f 18,8 nm, c , g 44,8 nm et d , h 59,6 nm. Atomes dans la rangée du haut et rangée du bas sont colorés en fonction de leurs valeurs CNA et hauteurs atomiques, respectivement

En plus de la plasticité dominée par le glissement de dislocation, la probabilité de transformation de phase dans le processus de coupe au diamant est également évaluée en effectuant une analyse RDF sur la zone de défaut dans la pièce et les copeaux formés. Le -Ce dans la structure fcc est d'abord exclu dans OVITO en utilisant l'algorithme CNA, et les atomes restants sont composés de zones de défauts comprenant bcc, hcp et d'autres atomes. Ensuite, une analyse RDF est effectuée sur la zone de défaut. Et la quantité de différentes phases de Ce peut être déduite du nombre de différents types d'atomes défectueux. La figure 5a montre que les trois pics du RDF de la zone de défaut sous la surface usinée coïncident bien avec les trois pics exacts du RDF du -Ce, suggérant l'apparition d'une transformation de phase du γ-Ce vers le -Ce. Alors que le δ-Ce est stable à haute température et basse pression, la transformation de phase γ ➔ δ qui s'est produite indique la dissipation de chaleur élevée générée lors du processus de coupe. De plus, étant donné que le -Ce a des propriétés mécaniques différentes de celles de la phase γ-Ce, le δ-Ce généré conduit à un usinage hétérogène dans le processus de coupe ultérieur. La figure 5b indique qu'il y a également des atomes δ-Ce détectés dans les copeaux formés, principalement en raison de la transformation de phase γ ➔ δ déclenchée à haute température dans la région de contact entre le copeau formé et la surface de coupe de l'outil de coupe. Cependant, la quantité de δ-Ce formé à la fois dans la zone défectueuse et dans la puce est très insignifiante, ce qui indique que la transformation de phase n'est pas importante dans la coupe diamantée du cérium.

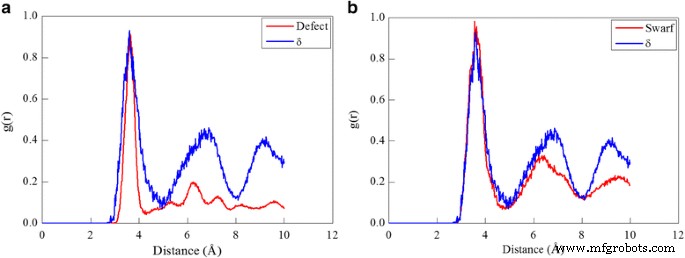
Analyse de la transformation de phase dans le processus de coupe ; (couleur en ligne) analyse de la transformation de phase dans la coupe diamantée de Ce(010) sous un angle de coupe de 0°. RDF de a pièce et b copeau après la coupe

Influence de l'angle de coupe

Avec la compréhension fondamentale des mécanismes d'usinage du cérium, l'influence de l'angle de coupe de l'outil de coupe sur la coupe du diamant est étudiée. La figure 6 représente les valeurs moyennes de la force de coupe et de la force normale pour les sept angles de coupe. La valeur moyenne de chaque composante de force est calculée en faisant la moyenne des valeurs de force instantanée dans la longueur de coupe allant de 10 à 35 nm. La figure 6 montre que la force de coupe est supérieure à la force normale pour chaque angle de coupe. Cependant, la valeur différentielle des deux composantes de force est plus prononcée pour un angle de coupe plus grand. De plus, la force de coupe et la force normale diminuent avec l'augmentation de l'angle de coupe. Selon la théorie de Merchant, avec l'augmentation de l'angle de coupe, l'angle du plan de cisaillement correspondant à l'énergie minimale augmente également, ce qui diminue en conséquence la force de coupe [37]. La variation de la force d'usinage en fonction de l'angle de coupe révélée par les simulations MD actuelles est en accord avec la théorie du marchand.

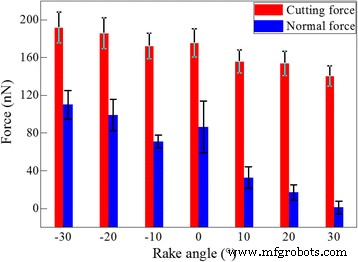
Dépendance de l'angle de coupe de la force d'usinage ; (couleur en ligne) influence de l'angle de coupe sur la force d'usinage

La figure 7a, b présente une vue de dessous de la structure du défaut sous la surface usinée après l'achèvement du processus de coupe au diamant avec un angle de coupe de -30° et 30°, respectivement. Pour chaque angle de coupe, les deux types de dislocation et la géométrie de la dislocation par rapport à la surface libre sont les mêmes. Cependant, la densité de dislocation est significativement plus élevée pour l'angle de coupe de -30° que pour l'angle de coupe de 30°, indiquant qu'une déformation plastique plus complexe s'est produite. La figure 7c présente le nombre de segments de dislocation restés dans la pièce après la coupe au diamant avec différents angles de coupe, indiquant que la densité de dislocation diminue avec l'augmentation de l'angle de coupe. Il convient de noter que différents types de luxations catégorisées par les vecteurs de Burgers, dont 1/2<110> luxation parfaite, 1/6<112> luxation partielle de Shockley, 1/6<110> luxation Stair-rod et 1/3 <111> Les luxations partielles de Frank, sont prises en compte sur la Fig. 7c. Dans le processus de coupe nanométrique, la déformation microscopique induite par la dislocation du matériau de la pièce a une forte corrélation avec les résultats d'usinage macroscopique en termes de force d'usinage et de morphologie de la surface usinée. Par exemple, l'interaction et la réaction des dislocations conduisent à la formation de structures de dislocation sessiles qui bloquent le mouvement de dislocation ultérieur ; par conséquent, l'écrouissage résultant conduit à une augmentation de la force d'usinage. L'annihilation des dislocations à la surface libre conduit à la récupération de la surface usinée, accompagnée de la formation d'un empilement de surface [38].

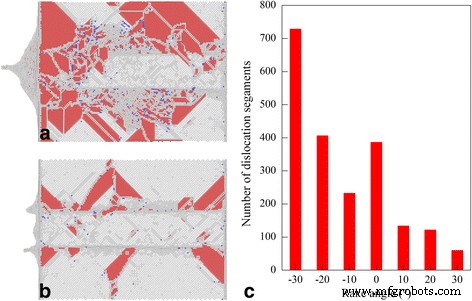
Structures de défauts générées avec différents angles de coupe ; (couleur en ligne) Instantanés MD des structures défectueuses après découpe du cérium avec un angle de coupe de a −30° et b 30°. Les atomes sont colorés en fonction de leurs valeurs CNA. c Numéro de luxation dépendant de l'angle de coupe

La figure 8 présente les morphologies des surfaces usinées après l'achèvement des processus de coupe pour différents angles de coupe. Le volume de surface empilé des deux côtés de la rainure formée est plus prononcé pour l'angle de coupe avec des valeurs négatives que celui avec des valeurs positives. De plus, la répartition de l'empilement en surface est moins uniforme pour un angle de coupe négatif que pour un angle de coupe positif. La figure 8c montre clairement la distribution asymétrique de l'empilement de surface le long de la rainure formée pour l'angle de coupe de -30°. On voit sur la figure 8 que le volume d'empilement de surface diminue avec l'augmentation de l'angle de coupe. Par conséquent, il est indiqué que l'angle de coupe de 30° est optimal pour la coupe diamantée du cérium pour la force d'usinage la plus faible, la densité de dislocation la plus faible et l'empilement de surface le plus faible que les autres angles de coupe.

Dépendance de l'angle de coupe des morphologies des surfaces usinées ; (couleur en ligne) morphologie de surface usinée avec différents angles de coupe :a −10°, b −20°, c −30°, d 10°, e 20°, et f 30°. Les atomes sont colorés en fonction de leurs hauteurs atomiques

Influence de l'orientation du cristal de la pièce en cérium

L'influence de l'orientation des cristaux sur la coupe diamantée du cérium sous l'angle de coupe optimal de 30° est également étudiée. Tous les paramètres d'usinage sont les mêmes pour Ce(010), Ce(110) et Ce(111). La figure 9 montre les variations de la force de coupe et du nombre de dislocations avec différentes orientations cristallines. La force de coupe de Ce(010) est nettement inférieure à celle de Ce(110) et Ce(111). Bien que le nombre de dislocations soit le plus faible dans Ce(111), la densité de dislocations dans Ce(010) est significativement inférieure à celle de Ce(110). Il est connu que la géométrie entre le plan de glissement et la surface libre varie avec l'orientation du cristal. Pour Ce(010) et Ce(110), les quatre plans de glissement {111} sont inclinés par rapport à la surface usinée. However, there is one {111} slip plane parallel to machined surface of Ce(111), in addition to three {111} inclined slip planes. While microscopic deformation of workpiece material is dominated by dislocation slips, the observed macroscopic machining results in terms of machined surface and machining force can also be influenced by machined surface morphology. Although the easy glide of dislocations on the {111} slip plane parallel to free surface is energetically favorable for the accommodation of plastic strain caused by cutting tool action, the resulting considerable surface pile up increases the machining resistance, which leads to a high cutting force.

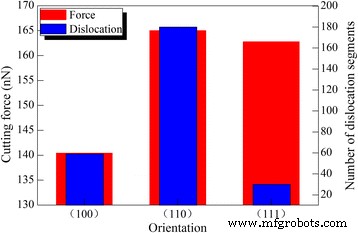
Crystal orientation dependence of cutting force and dislocation number; (color online) crystal orientation dependence of cutting force and dislocation number

Figure 10a–c presents machined surface morphology of Ce(010), Ce(110), and Ce(111), respectively, indicating that the crystal orientation has a strong influence on machined surface quality. The volume of surface pile up is the smallest for Ce(010), followed by Ce(111), and the largest for Ce(110). Correspondingly, the material removal in the form of chip is the most pronounced for Ce(010). Furthermore, it is seen that the surface pile up of Ce(111) on both side of formed groove presents the highest symmetry, while that of Ce(110) is the worst. Therefore, it is indicated that the crystal orientation of (010) is optimal for the diamond cutting of cerium due to its low machining force, low dislocation density, and low surface pile up.

Crystal orientation dependence of machined surface morphology; (color online) crystal orientation dependence of machined surface morphology. Atoms are colored according to atomic heights. Crystal orientation. un (010). b (110). c (111)

Conclusions

In summary, we perform MD modeling and simulation to elucidate the underlying mechanisms of cerium under the ultra-precision diamond cutting. The EAM and Morse potentials are respectively employed to describe atomic interactions within cerium workpiece and the interactions between cerium workpiece and diamond cutting tool. The elastic constants, mechanical properties, and propensity of phase transformation of cerium phases are evaluated, which demonstrates the feasibility of predicting phase transformation of cerium by the current established MD model. Subsequent MD simulations of diamond cutting reveal that the plastic deformation of cerium is governed by dislocation nucleation and subsequent glide, which is similar with other fcc metals. In addition, there is γ ➔ δ phase transformation occurred within both machined surface and formed chip. It is found that high quality of machined surface and low machining force can be achieved in the diamond cutting of cerium with the optimal machining conditions, i.e., a rake angle of 30° for a crystal orientation of (010).