Effets de la taille et de l'agrégation/agglomération des nanoparticules sur les propriétés interfaciales/d'interphase et la résistance à la traction des nanocomposites polymères

Contexte

Les nanocomposites présentent des propriétés substantielles par seulement une faible teneur en nanocharge [1,2,3,4,5]. Les propriétés importantes des nanocomposites polymères sont à l'origine d'un large éventail d'applications dans diverses technologies telles que les matériaux et les biens avancés, les médicaments, les dispositifs énergétiques et les capteurs [6]. Les études sur différents types de nanocomposites polymères visent à obtenir des produits de haute performance par un processus de fabrication simple et à faible coût.

Les propriétés considérables des nanocomposites polymères sont attribuées aux bonnes propriétés interfaciales entre la matrice polymère et les nanoparticules telles que la zone interfaciale et l'interaction/adhérence à l'interface [7,8,9,10,11,12,13]. Les niveaux élevés de propriétés interfaciales conduisent à la formation d'une autre phase comme interphase autour des nanoparticules qui est différente à la fois de la matrice polymère et des nanoparticules montre l'avantage des nanocomposites par rapport aux micro-composites conventionnels [14,15,16,17,18]. De nombreuses recherches théoriques sur les propriétés interfaciales/interphases ont fourni une grande quantité d'informations pour atteindre les propriétés souhaitables. Cependant, la grande surface spécifique des nanoparticules et la forte interaction attractive entre les particules entraînent l'agrégation/agglomération [19, 20]. Les collectifs forts et denses de nanoparticules dénotent l'agrégation, mais les particules à joint lâche montrent l'agglomération qui peut être rompue par la contrainte mécanique [21].

L'agrégation/agglomération de nanoparticules réduit l'amélioration potentielle des propriétés mécaniques des nanocomposites, en raison de la restriction de la zone interfaciale [22, 23]. Par conséquent, le principal défi dans la production de nanocomposites comprend la réalisation de petites nanoparticules et une bonne dispersion des nanoparticules. Il est vital de surmonter les forces d'attraction entre les nanoparticules produisant l'agrégation/agglomération, au lieu de perturber la structure des nanoparticules. Étonnamment, Dorigato et al. [24] ont suggéré un modèle qui montre que l'agrégation de la charge primaire renforce les nanocomposites polymères, tandis que les nanoparticules agglomérées induisent couramment des effets négatifs sur les performances mécaniques des nanocomposites polymères [21, 25]. En conséquence, l'étude sur l'agrégation/agglomération des nanoparticules est nécessaire pour révéler ses effets réels sur les propriétés des nanocomposites. Bien que la taille des nanoparticules soit considérée comme un avantage attrayant dans les nanocomposites polymères, les effets de l'isolement ou de l'agrégation/agglomération sur les principales propriétés des nanoparticules telles que le nombre, la surface et la surface spécifique n'ont pas été étudiés dans la littérature. De plus, l'agrégation/agglomération de nanoparticules a été considérée comme un terme général qui modifie qualitativement le comportement des nanocomposites. De plus, les rôles possibles des dimensions des nanoparticules et de l'interphase sur les propriétés interfaciales/interphases n'ont pas été décrits dans des études précédentes.

Méthodes

Dans cet article, les effets de la taille et de la densité de la charge sur le nombre, la surface, l'efficacité de raidissement et la surface spécifique des nanoparticules dans les nanocomposites polymères sont expliqués par des équations appropriées. De plus, l'agrégation/agglomération de nanoparticules est supposée être de grosses particules et leurs influences sur divers termes sont révélées. De même, les rôles possibles des tailles de nanoparticules et d'interphases dans les paramètres interfaciaux/interphases et la résistance à la traction des nanocomposites sont discutés. L'objectif principal de cet article est sur les nanoparticules sphériques, mais d'autres géométries de nanoparticules peuvent être étudiées par le développement des équations suggérées.

Le nombre de nanoparticules isolées sphériquement dans un nanocomposite peut être calculé par le poids des nanoparticules (W _f ) comme :

où d _f et R sont respectivement la densité et le rayon des nanoparticules. Dans cette condition, la surface totale des nanoparticules dispersées est donnée par :

Un peut être considérée comme la zone d'interface entre la matrice polymère et les nanoparticules. Remplacement de N de l'éq. 1 dans l'éq. 2 mène à :

qui corrèle le A avec W _f , d _f , et R .

Chaque nanoparticule introduit un effet de rigidification dans la matrice polymère par implication mécanique des chaînes polymères. Le niveau de partage des contraintes entre la matrice polymère et les nanoparticules dépend de la surface interfaciale et de la rigidité des nanoparticules. En conséquence, un nouveau paramètre comme l'efficacité de rigidification des nanoparticules peut être défini comme :

où E _f est le module de Young des nanoparticules. L'efficacité de rigidification en fonction des propriétés des nanoparticules exprime la capacité des nanoparticules à rigidifier des nanocomposites. De plus, la surface spécifique des particules est exprimée par :

où m et v sont respectivement la masse totale et le volume des nanoparticules. Ce paramètre exprime la surface de 1 g de particules et ne dépend donc pas de la concentration de nanoparticules dans le nanocomposite.

Maintenant, la résistance à la traction et les propriétés interfaciales/interphases sont données par des équations simples. Pukanszky [26] a suggéré un modèle pour la résistance à la traction des composites en fonction de la teneur en charge et des propriétés interfaciales/interphases comme :

où σ _m montre la résistance à la traction de la matrice polymère et φ _f est la fraction volumique de nanocharge. Ce modèle a été initialement suggéré pour les composites, mais ce modèle a montré de bons accords avec les résultats expérimentaux de différents nanocomposites polymères. Un bon accord est obtenu entre les données expérimentales de résistance à la traction et les prédictions de l'équation de Pukanszky dans de nombreux échantillons tels que PP/SiO₂ [27], PEEK/SiO₂ [28], PVC/CaCO₃ [29], PP/CaCO₃ [30], et PVC/SiO₂ [31] calcul du B paramètre comme 4.12, 3.15, 3.07, 2.5 et 2.1, respectivement. Ces exemples valident l'application du modèle Pukanszky pour la résistance à la traction des nanocomposites polymères.

B est un paramètre interfacial qui montre le niveau d'adhésion interfaciale par :

où t et σ _i sont respectivement l'épaisseur et la force de l'interphase.

Remplacement de A _c de l'éq. 5 dans cette dernière équation présente :

L'application de l'équation ci-dessus dans le modèle Pukanszky offre la force relative (σ /σ _m ) comme :

qui lie explicitement la résistance à la traction aux propriétés de charge et d'interphase. En outre, il convient d'indiquer les effets de taille, qui existent sans aucun doute lors de la modélisation de la fracture [32,33,34].

La fraction volumique d'interphase (φ _i ) pour les nanocomposites contenant des nanoparticules sphériques peut être envisagée [35] par :

dans lequel t = 0 résultats dans φ _i = 0 indiquant l'absence d'interphase dans le nanocomposite. Les modèles analytiques de cette étude peuvent être applicables là où d'autres modèles tels que la zone cohésive décrivent les régions d'interphase. Certaines études antérieures ont considéré l'interphase par certains modèles tels que les éléments finis 2D [36, 37].

Dans nos précédents travaux [38], a Le paramètre d'interphase pour les nanocomposites polymères renforcés de nanoparticules sphériques a été défini comme :

où E _i est le module d'interphase. Cette équation corrèle le a à divers paramètres effectifs de nanocharge et d'interphase. un a été calculé pour certains nanocomposites allant de 0,8 à 19 [38]. Il a été signalé qu'un niveau plus élevé de a introduit un meilleur module dans le nanocomposite.

Résultats et discussion

Dans la première partie de cette section, les effets de la taille et de la densité sur différentes propriétés des nanoparticules sont tracés par des tracés de contour et les résultats sont discutés pour clarifier l'influence de l'agrégation/agglomération. À l'étape suivante, les rôles du rayon des nanoparticules (y compris l'agrégation/agglomération) et de l'épaisseur d'interphase dans les propriétés interfaciales/interphases et les performances des nanocomposites sont étudiés.

La figure 1 illustre l'agrégation/agglomération de nanoparticules dans un nanocomposite. Lorsque les nanoparticules isolées et dispersées sont accumulées, on peut supposer qu'une grande nanoparticule est formée. Selon la Fig. 1, si des nanoparticules isolées avec R agrégat/agglomérat de rayon, une grosse particule est produite avec un rayon élevé. En conséquence, l'agrégation/agglomération de nanoparticules peut être physiquement assumée par la croissance de la taille des particules dans les nanocomposites. Cette occurrence affecte les caractéristiques des nanoparticules et de l'interphase qui modifient finalement le comportement des nanocomposites.

Illustration schématique de l'agrégation/agglomération de nanoparticules dans des nanocomposites polymères. Lorsque plusieurs nanoparticules de rayon R sont agrégés/agglomérés, une grosse particule se forme

La figure 2 montre les rôles de R et d _f en ln (N) et A niveaux à W constant _f = 2 g. D'après la figure 2a, faible N est observé par les valeurs élevées de R et d _f , mais N augmente lorsque R et d _f diminuer. Ainsi, la densité et la taille des nanoparticules affectent inversement le nombre de particules dans les nanocomposites polymères à concentration de charge constante. Les petites nanoparticules à faible densité produisent un grand nombre de nanoparticules dans les nanocomposites, tandis que les nanoparticules grosses et denses produisent peu de particules. En conséquence, les agrégats/agglomérats diminuent considérablement le nombre de nanoparticules dans les nanocomposites à concentration de charge constante.

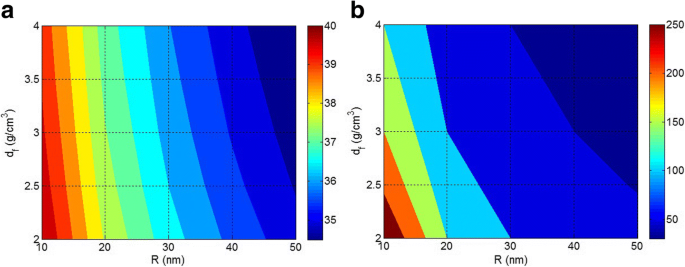
Graphiques de contour pour montrer les rôles de R et d _f paramètres dans a ln (N ) et b Un (m ² ) à W _f = 2 g

La figure 2b illustre les effets de R et d _f paramètres sur la surface totale des nanoparticules (A en m ² ) à W _f = 2 g. La surface des nanoparticules est supposée être la surface interfaciale entre le polymère et les nanoparticules transférant la contrainte de la matrice aux nanoparticules. La contrainte peut être efficacement transportée du polymère aux nanoparticules pour améliorer les propriétés mécaniques, lorsque la zone interfaciale est suffisamment grande [39, 40]. Comme observé dans la Fig. 2b, la plus grande zone interfaciale est obtenue par les plus petites plages de R et d _f . Il est également intéressant de noter que seulement 2 g de nanoparticules isolées et bien dispersées avec R = 10 nm et d _f = 2 g/cm ³ produire environ 250 m ² zone interfaciale avec matrice polymère. Cependant, la zone interfaciale se réduit en augmentant la taille et la densité des nanoparticules et A moins de 50 m ² est obtenu à R> 40 nm et d _f > 3 g/cm ³ . La différence significative entre les zones interfaciales à différentes tailles de particules indique que la taille des nanoparticules est un paramètre important dans les nanocomposites. Les grosses nanoparticules provoquent une petite surface interfaciale qui détériore l'avantage significatif des nanoparticules dans les nanocomposites. Il convient de noter que la concentration de charge dans les nanocomposites peut ne pas être trop élevée par rapport aux micro-composites, mais la surface extraordinaire des nanoparticules entraîne généralement l'interaction entre les particules et l'agrégation/agglomération. En conséquence, bien que les teneurs élevées en nanoparticules dans les nanocomposites renforcent l'accumulation, l'agrégation/agglomération de nanoparticules se produit généralement dans les nanocomposites polymères à différentes concentrations de charge qui diminuent la surface interfaciale et affaiblissent les performances.

La figure 3a affiche les courbes de niveau de ln (SE) en fonction de R et d _f à W _f = 2 g et E _f = 100 GPa. L'efficacité de rigidification des nanoparticules augmente lorsque de petites nanoparticules à faible densité sont incorporées dans la matrice polymère, démontrant que la taille des nanoparticules joue un rôle efficace dans la rigidification des nanoparticules dans les nanocomposites polymères. D'autre part, les nanoparticules agrégées/agglomérées détériorent les performances des nanocomposites polymères par réduction de l'efficacité des nanoparticules. Les petites nanoparticules à faible densité augmentent de manière significative la rigidité des nanocomposites grâce au grand niveau de transfert de contrainte entre les chaînes polymères et les nanoparticules. Une étude précédente dans ce domaine a expliqué la physique de l'influence du rayon de remplissage sur le transfert de contrainte de la matrice polymère à la fibre en utilisant les simulations de dynamique moléculaire [41]. Cependant, les particules grosses et denses ne peuvent pas introduire la rigidité élevée des nanoparticules dans la matrice polymère, suggérant un composite avec une rigidité médiocre. Par conséquent, les caractéristiques des nanoparticules contrôlent de manière significative les propriétés des nanocomposites.

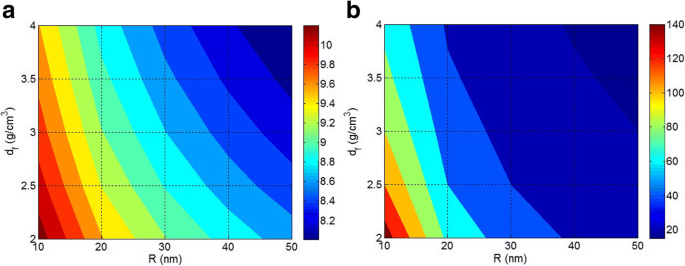
Les effets de R et d _f sur a ln (SE) avec ln (m ² unité GPa) et b Un _c (m ² /g) à W _f = 2 g et E _f = 100 GPa

La figure 3b montre également les niveaux de A _c paramètre à différents R et d _f valeurs à W _f = 2 g et E _f = 100 GPa. On constate que le meilleur A _c est obtenu par des nanoparticules petites et de faible densité, tandis que la pire est produite par des particules grosses et denses. Le A _c valeur d'environ 140 m ² /g est obtenu par R = 10 nm et d _f = 2 g/cm ³ , tandis que A _c niveau inférieur à 20 m ² /g est représenté par une grande taille de particule et une densité élevée. En conséquence, R et d _f les paramètres montrent des effets négatifs sur A _c dans les nanocomposites polymères. Il est conclu que A _c paramètre exprimant l'aire interfaciale de 1 g de nanoparticules isolées donne les meilleurs niveaux par petites nanoparticules. En conséquence, les grandes nanoparticules ou agrégats/agglomérats ne peuvent pas produire un A considérable _c ce qui diminue l'efficacité des nanoparticules dans les nanocomposites polymères. Il est connu que les performances des nanocomposites telles que les propriétés mécaniques, ignifuges et barrières sont directement liées à la zone interfaciale entre le polymère et les nanoparticules [10, 42]. Un grand A _c peut produire des niveaux acceptables pour les propriétés des nanocomposites avec une faible quantité de nanoparticules, en raison de la zone interfaciale élevée entre la matrice polymère et les nanoparticules. Par conséquent, le contrôle de la taille et de la densité des nanoparticules est un défi dans les nanocomposites pour créer les meilleures propriétés.

Maintenant, les effets de la taille des nanoparticules et des interphases sur les propriétés interfaciales/interphases et la résistance à la traction des nanocomposites sont expliqués par les équations proposées. La figure 4 illustre les effets de R et t sur B paramètre interfacial et résistance à la traction par le modèle de Pukanszky (Eq. 6) à σ _i /σ _m = 5 et φ _f = 0,02. D'après la figure 4a, le B le niveau de 13 est obtenu par les nanoparticules les plus petites et l'interphase la plus épaisse. Aussi, B diminue à moins de 3 lorsque la taille des nanoparticules augmente jusqu'à environ 40 nm et que l'épaisseur d'interphase diminue à moins de 10 nm. Par conséquent, les tailles des nanoparticules et l'interphase jouent des rôles différents dans B paramètre. En outre, il convient de noter que les petites nanoparticules sans formation d'une forte interphase ne peuvent pas donner un B élevé dans les nanocomposites polymères. En revanche, une interphase épaisse (t = 25 nm) entourant les grosses nanoparticules (R = 50 nm) n'améliore que le B paramètre à environ 4. Par conséquent, les dimensions des nanoparticules et de l'interphase sont importantes pour obtenir un niveau élevé de B dans les nanocomposites. Cependant, à niveau constant d'épaisseur d'interphase, la croissance de la taille des nanoparticules par agrégation/agglomération diminue B paramètre démontrant les effets négatifs des agrégats/agglomérats sur les propriétés interfaciales/interphases.

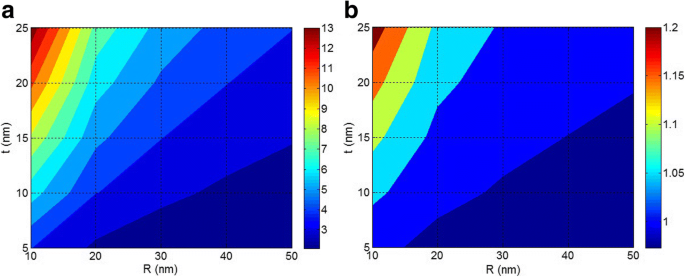
un B paramètre interfacial et b résistance à la traction relative par le modèle Pukanszky à différentes plages de R et d _f et constant σ _i /σ _m = 5 et ϕ _f = 0,02

La figure 4b montre également les effets de R et t paramètres sur la résistance à la traction des nanocomposites par le modèle de Pukanszky. On observe que les petites nanoparticules et l'interphase épaisse améliorent la résistance des nanocomposites. Cependant, une mauvaise résistance est observée par les grosses particules et l'interphase mince. Par conséquent, les deux R et t paramètres affectent la résistance à la traction des nanocomposites. De plus, on constate que la résistance des nanocomposites diminue lorsque la taille des nanoparticules augmente, en raison de l'agrégation/agglomération. En conséquence, il est essentiel d'isoler et de disperser les nanoparticules dans la matrice polymère à petite taille pour obtenir les meilleures performances. Les nanoparticules ayant naturellement tendance à s'agréger/s'agglomérer, une modification de leur surface ou une fonctionnalisation de chaînes polymères peut empêcher l'accumulation [19, 43, 44].

La figure 5 illustre les dépendances de la fraction volumique d'interphase (φ _i ) et a paramètre d'interphase sur R et t paramètres à φ _f = 0,02, E _f = 100 GPa, et E _i = 50 GPa. Selon la figure 5a, les nanoparticules les plus petites et l'interphase la plus épaisse donnent le niveau le plus élevé de φ _i comme 0,8 ce qui renforce significativement le nanocomposite. Ce niveau de φ _i est plus que φ _f démontrer les rôles efficaces de R et t paramètres dans les performances des nanocomposites. De plus, φ _i diminue à environ 0 à R> 30 nm, c'est-à-dire une interphase épaisse (t = 25 nm) ne peut pas faire un φ élevé _i dans les nanocomposites polymères lorsque de grosses nanoparticules sont incorporées dans la matrice polymère. Cette occurrence montre le rôle important de la taille des nanoparticules dans la formation des régions d'interphase. Ainsi, la taille des nanoparticules modifie considérablement les propriétés d'interphase, révélant que l'agrégation / agglomération de nanoparticules diminue principalement la concentration d'interphase, ce qui entraîne un module et une résistance médiocres des nanocomposites [5, 45]. Il convient de mentionner que les régions d'interphase peuvent se chevaucher dans les systèmes contenant une concentration élevée de charge. Par conséquent, l'équation exprimée pour φ _i (Eq. 10) est raisonnable pour les nanocomposites normaux contenant une faible teneur en charge.

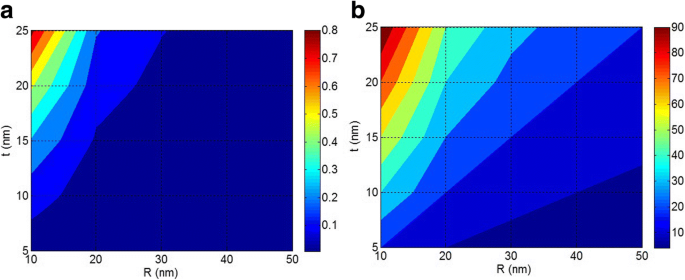
La corrélation de a ϕ _i et b un paramètre d'interphase à R et t paramètres à ϕ _f = 0,02, E _f = 100 GPa, et E _i = 50 GPa

La figure 5b montre également les effets de R et t niveaux sur a paramètre d'interphase. un augmente par les petites nanoparticules et l'interphase épaisse, alors qu'il donne moins de valeurs (inférieures à 10) à R> 40 nm et t < 10 nm. Cette preuve révèle que a dépend à la fois de R et t paramètres. Depuis un a élevé Ce paramètre améliore le module de Young des nanocomposites [38], de petites nanoparticules et une interphase épaisse sont souhaitables pour les performances des nanocomposites. Selon la Fig. 5b, les agrégats/agglomérats de nanoparticules (haut R ) produisent un léger a événement par interphase épaisse. Cet événement indique qu'une forte interphase ne peut pas donner un grand a ou à module élevé lorsque les nanoparticules sont agrégées/agglomérées dans des nanocomposites. En conséquence, les agrégats/agglomérats de nanoparticules provoquent des effets négatifs sur les propriétés des nanocomposites polymères. Sur la base des remarques mentionnées, l'agrégation/agglomération affaiblit les avantages des nanoparticules et les propriétés d'interface/interphase ; par conséquent, les nanoparticules ne peuvent pas présenter un fort renforcement dans les nanocomposites polymères.

Conclusions

Les effets de la taille et de la densité de la charge ainsi que de l'épaisseur d'interphase sur les caractéristiques des nanoparticules et les propriétés d'interface/interphase ont été étudiés par des équations simples. De plus, les agrégats/agglomérats de nanoparticules ont été supposés être de grosses particules et leurs influences sur les paramètres d'interphase et la résistance à la traction des nanocomposites ont été discutées. La petite taille et la faible densité entraînent des niveaux significatifs pour le nombre, la surface, l'efficacité de raidissement et la surface spécifique des nanoparticules. Seulement 2 g de petites nanoparticules bien dispersées (R = 10 nm) avec d _f = 2 g/cm ³ peut produire environ 250 m ² zone interfaciale avec matrice polymère. D'autre part, la grande taille et les agrégats/agglomérats affaiblissent les attributs positifs des nanoparticules dans les nanocomposites. Les petites nanoparticules et l'interphase épaisse présentent les niveaux élevés de B paramètre, résistance à la traction, fraction volumique d'interphase et a paramètre d'interphase. B diminue à moins de 3 lorsque la taille des nanoparticules atteint environ 40 nm et que l'épaisseur d'interphase diminue à moins de 10 nm. Cependant, B = 13 est obtenu par les plus petites nanoparticules (R = 10 nm) et l'interphase la plus épaisse (t = 25 nm). Cette occurrence confirme que les propriétés interfaciales/interphases dépendent de la taille des nanoparticules à côté de l'interaction/adhérence interfaciale. De plus, les grosses nanoparticules produisent de faibles propriétés interfaciales/interphases et une faible résistance à la traction, même à une épaisseur d'interphase élevée, révélant le rôle principal de la taille des particules. Les nanoparticules les plus petites et l'interphase la plus épaisse donnent le plus haut niveau de φ _i , tandis que φ _i diminue jusqu'à environ 0 à R> 30 nm. Cette preuve démontre que seule une interphase épaisse (t = 25 nm) ne peut pas faire un φ élevé _i lorsque de grosses nanoparticules ou agrégats/agglomérats sont présents dans des nanocomposites. En conséquence, les nanoparticules agrégées/agglomérées affectent négativement les propriétés interfaciales/interphases et la résistance à la traction des nanocomposites polymères.