Théorème de Tellegen - Exemples résolus et simulation MATLAB

Théorème de Tellegen – Guide étape par étape avec exemples résolus

Qu'est-ce que le théorème de Tellegen ?

Théorème de Tellegen a été publié par un ingénieur électricien et inventeur néerlandais Bernard D.H. Tellegen en 1952. Ce théorème est le théorème le plus important et le plus fondamental parmi les autres théorèmes en analyse de réseau. La plupart des autres théorèmes sont dérivés de ce théorème.

Le théorème de Tellegen dépend de la loi de Kirchhoff. Par conséquent, ce théorème peut s'appliquer au réseau qui obéit à la loi de Kirchhoff. Ce théorème peut être appliqué à la large gamme du réseau ayant des éléments linéaires ou non linéaires, variant dans le temps ou non, passifs ou actifs.

Le théorème de Tellegen stipule que ;

Le théorème de Tellegen fonctionne sur la base du principe de la loi de conservation de l'énergie. Ce théorème est utilisé dans des applications chimiques et biologiques pour trouver le comportement dynamique du réseau physique. En traitement du signal, ce théorème est utilisé pour concevoir des filtres.

• Article connexe :Théorème de Thevenin. Guide étape par étape avec exemple résolu

Équation mathématique

Pour une analyse générale du théorème, nous considérons que le nombre « n » d'éléments est donné dans le réseau. Le courant instantané traversant l'élément est i₁ , je₂ , je₃ , …., je_n . Et la tension instantanée de cette branche est v₁ , v₂ , v₃ , …., v_n .

Par conséquent, le courant et la tension instantanés de l'élément-1 sont i₁ et v₁ . La puissance instantanée (p₁ ) consommée par cet élément est v₁ je₁ .

p ₁ =v ₁ je ₁

La puissance instantanée de l'élément-2 est (p ₂ );

p ₂ =v ₂ je ₂

De même, la puissance instantanée du n ^ième l'élément est (p _n );

p_n =v_n je_n

Selon le théorème de Tellegen, la somme de toutes les puissances instantanées est nulle. Cela signifie que nous devons additionner toute la puissance instantanée p₁ , p₂ , p₃ , …., p_n .

p ₁ + p ₂ + p ₃ + … + p_n = 0

v ₁ je ₁ + v ₂ je ₂ + v ₃ je ₃ + … + v_n je_n  = 0

Sous une forme générale, nous pouvons écrire l'équation ci-dessus pour le k ^ème succursale ;

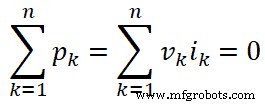
Où,

• n =nombre total d'agences dans le réseau
• v_k =tension instantanée du k ^ème succursale
• i_k =courant instantané du k ^ème succursale
• p_k =puissance instantanée du k ^ème succursale

Maintenant, considérons la figure ci-dessous car la branche AB est égale à la branche k.

Par conséquent, la tension instantanée v_k ;

v_k =v_a – v_b

Et le courant instantané traversant la branche (a à b) est i_k ;

i_k =je_ab

Ainsi, la puissance instantanée p_k est ;

p_k =v_k je_k =(v_a –v_b ) je_ab ….. (1)

Maintenant, nous considérons la direction opposée du courant instantané (b vers a) ;

i_ab =– i_ab

Tension instantanée ;

v_k =v_b – v_un

La puissance instantanée p_k est ;

p_k =v_k je_k =(v_b – v_a ) je_ba ….. (2)

Sommation des équations 1 et 2 ;

2v_k je_k =(v_a –v _b ) je _ab + (v_b – v_a ) i_ba

v_k je_k =1/2 [(v_a –v _b ) je _ab + (v_b – v_a ) je_ba ] ….. (3)

Cette équation peut être écrite comme ci-dessous pour n-branches ;

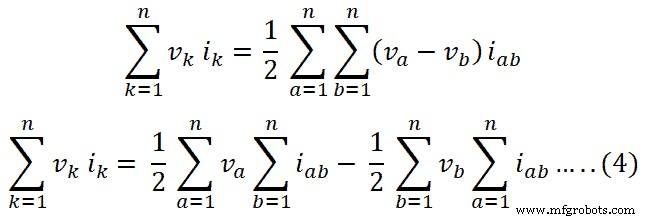
Selon la loi actuelle de Kirchhoff, la somme algébrique du courant est nulle à un nœud du circuit.

Par conséquent,

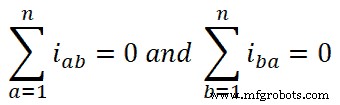
Si nous mettons cette valeur dans l'équation-4, nous obtenons ;

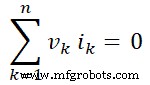
Ainsi, il est prouvé que la somme des puissances délivrées au réseau est nulle. Par conséquent, le théorème de Tellegen est prouvé. Il est également décrit que la somme des puissances absorbées par les éléments du réseau est égale à la somme des puissances délivrées par les sources.

• Article connexe : Théorème de Norton. Guide étape par étape avec exemple résolu

Étapes à suivre pour le théorème de Tellegen

Nous devons suivre les étapes ci-dessous pour résoudre tout réseau électrique par le théorème de Tellegen.

Étape 1 : Nous devons trouver un certain nombre de branches dans le réseau électrique donné. Ensuite, trouvez la puissance dissipée sur chaque branche. Pour trouver la puissance, nous devons trouver la tension ou le courant de cette branche en utilisant n'importe quelle méthode d'analyse conventionnelle.

Étape 2 : Trouvez la puissance instantanée de chaque branche.

Étape 3 : La branche qui a une source d'énergie qui est considérée comme une branche de fourniture d'énergie. Et la branche comportant d'autres éléments est considérée comme une branche absorbant la puissance. Identifiez maintenant la branche de fourniture d'énergie et la branche d'absorption d'énergie.

Étape 4 : Supposons un signe positif dans la branche de fourniture de puissance et une chute de tension négative dans la branche d'absorption de puissance. Vous pouvez également supposer des signes inversés. Mais ne peut pas changer tout au long de l'exemple.

Étape 5 : Pour justifier le théorème de Tellegen, nous devons ajouter toute la puissance calculée à partir de toutes les branches. Et cette somme est toujours nulle.

• Article connexe :  Analyse de circuit SUPERMESH – Étape par étape avec exemple résolu

Comprenons avec un exemple.

Exemple de résolution du théorème de Tellegen

Exemple #1

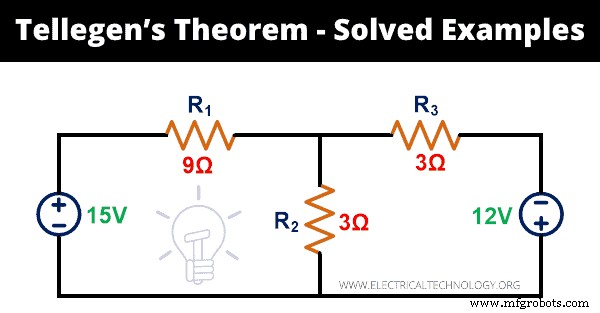
Justifiez le théorème de Tellegen pour le réseau ci-dessous.

Solution :

Étape 1 : Le réseau de circuits donné a 5 branches. Pour calculer la puissance instantanée, nous devons trouver le courant qui traverse chaque branche. Pour cela, nous appliquerons KVL au réseau.

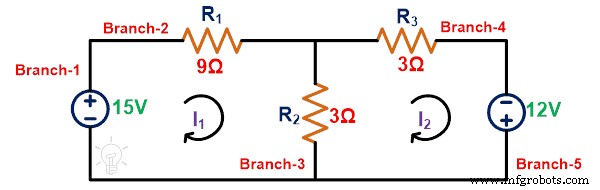
Appliquer KVL à la boucle-1 ;

15 =12je ₁ – 3je ₂

Appliquer KVL à la boucle-2 ;

12 =– 3je ₂ + 6je ₂

En résolvant les équations ci-dessus, nous pouvons trouver les valeurs du courant de boucle I₁ et moi₂ . Et ces valeurs sont :

Je ₁ =2A

Je ₂ =3A

Étape 2 : Le courant passant par la branche-3 est ;

Je _{1 2} =je ₂ – je ₁ =3 – 2 =1A

Nous avons du courant qui circule dans toutes les branches. Maintenant, trouvez la puissance de chaque branche.

P ₁ =V I ₁ =15x2 =30W

P ₂ =R ₁ je ₁ ² =9x4 =36W

P ₃ =R ₁ je ₁₂ ² =3x1 =3W

P ₄ =R ₃ je ₂ ² =3x9 =27W

P ₅ =V I ₂ =12x3 =36W

Étape 3 : Il y a deux branches ayant des sources. Ces branches sont des branches de fourniture d'énergie et les trois autres branches sont des branches d'absorption d'énergie.

Ici, pour cet exemple, nous supposons que le signe de la branche de fourniture de puissance est positif et que le signe de la branche d'absorption de puissance est négatif. Par conséquent, les branches 1 et 5 sont des branches de fourniture d'énergie et les autres branches sont des branches d'absorption d'énergie.

Étape 4 : Le signe de la puissance P₁ et P₅ est positif (branches délivrant de la puissance) et le signe de P₂ , P₃ , et P₄ est négatif (branches absorbant la puissance).

Étape 5 : Maintenant, nous devons trouver une somme de puissance dissipée par toutes les branches.

P ₁ – P ₂ – P ₃ – P ₄ + P ₅ =30W – 36W – 3W – 27W + 36W =0W

Ainsi, la somme de la puissance instantanée est nulle. Et donc, ce théorème est prouvé.

• Article connexe :Analyse de circuit SUPERNODE – Étape par étape avec exemple résolu

Exemple #2

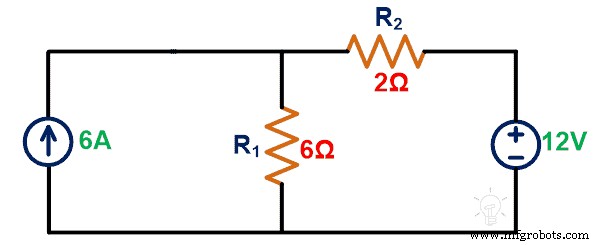
Trouvez la tension aux bornes d'une source de courant de 6 A à l'aide du théorème de Tellegen.

Solution :

Étape 1 : Nous devons calculer la tension ou le courant qui traverse l'élément. Pour cela, nous appliquons KCL ou KVL au réseau donné.

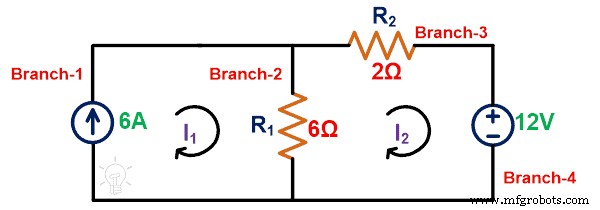
Appliquer KVL à la boucle-2 ;

-12 =8I ₂ – 6je ₁

Le courant passe par la branche ayant la source de courant est I ₁;

Je ₁ =6A

Mettez cette valeur dans l'équation ci-dessus ;

-12 =8I ₂ – 6(6)

-12 =8I ₂ – 36

36 - 12 =8I ₂

24 =8je ₂

Je ₂ =3A

Étape 2 : Le courant passe par la branche-2 est ;

Je ₁₂ =je ₁ – je ₂ =6 – 3 =3A

Maintenant, trouvez la puissance de chaque branche ;

P ₁ =V I ₁ =V x 6 =6 x V

P ₂ =R ₁ je ₁₂ ² =6x9 =54W

P ₄ =R ₂ je ₂ ² =2x9 =18W

P ₄ =V I ₂ =-12 x 3 =-36W

Étape 3 : Ici, deux branches ayant des sources d'énergie. Par conséquent, nous devons considérer ces branches comme des branches fournissant de l'énergie. Et réglez le signe positif sur la puissance instantanée.

Les deux autres branches n'ayant que des résistances. Ainsi, ces branches sont des branches absorbant la puissance et définissent le signe négatif de la puissance instantanée.

Étape 4 : Puissance P₁ et P₄ ont un signe positif et une puissance P₂ et P3 ont un signe négatif.

Étape 5 : Maintenant, nous devons résumer toute la puissance instantanée.

P ₁ – P ₂ – P ₃ + P ₄ =0W

P ₁ – 54 – 18 + 36 =108W

La puissance délivrée par la source de courant 6A est de 108W. Par conséquent, la tension aux bornes de la source de courant est calculée par :

P ₁ =V I

108W =V x 6A

V =18 V

Par conséquent, la tension aux bornes de la source de courant est de 18 V.

• Message connexe : Théorème de transfert de puissance maximale pour les circuits CA et CC

Analyse et simulation du théorème de Tellegen à l'aide de MATLAB  

Objectif :

Démontrer le théorème de Tellegen pour le schéma de circuit donné dans l'exemple ci-dessus.

Exigence : MATLAB

Théorie :

Selon le théorème de Tellegen, la puissance instantanée de sommation de toutes les branches est égale à zéro. Pour prouver ce théorème, nous devons calculer la puissance instantanée de toutes les branches.

Pour trouver la puissance instantanée, nous devons calculer la tension ou le courant de toutes les branches. Pour cela, on peut utiliser les théorèmes KCL ou KVL. Mais ici, nous utiliserons le modèle MATLAB Simulink pour trouver le courant et la tension.

Nous pouvons également utiliser d'autres logiciels comme multisim, psim, etc. Nous allons construire un schéma de circuit dans le modèle Simulink. Grâce au modèle Simulink, vous pouvez trouver la tension et le courant de chaque branche.

Après cela, vous pouvez trouver la puissance instantanée à partir de la tension et du courant. Vous pouvez directement trouver la puissance instantanée à partir de certains logiciels.

Modèle MATLAB Simulink

La figure ci-dessous montre le schéma de circuit de l'exemple ci-dessus.

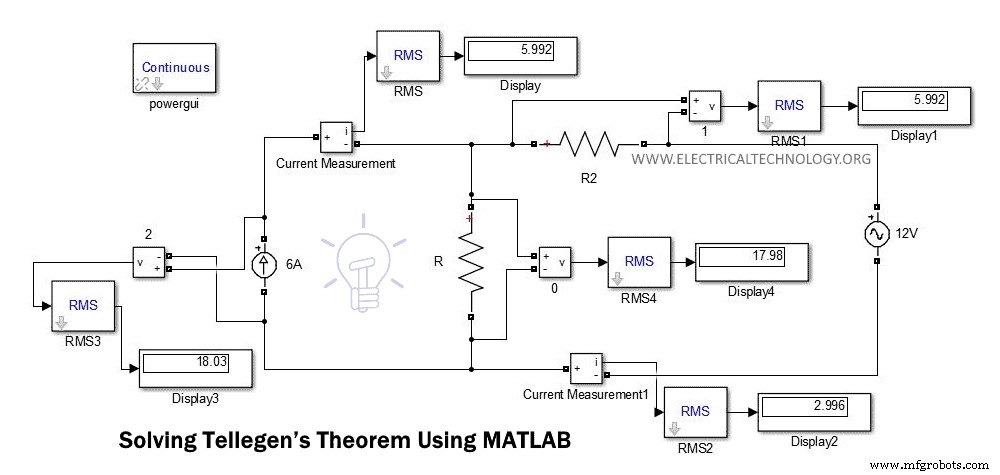
Sur cette figure, nous pouvons directement trouver la tension et le courant à partir de l'affichage. Vous pouvez comparer ces valeurs en calculant la tension et le courant à l'aide de KCL ou KVL.

Calcul

Après avoir calculé la tension ou le courant, vous pouvez trouver la puissance instantanée. Ou vous pouvez trouver directement la puissance instantanée à partir du logiciel. Tout ce dont nous avons besoin, c'est d'une puissance instantanée. Et après cela, nous devons ajouter tous les pouvoirs.

La somme des puissances est toujours nulle. Pour cet exemple, nous comparons la valeur de tension et de courant trouvée à partir de Simulink et les mêmes valeurs calculées dans l'exemple précédent en utilisant KVL et KCL. Ces valeurs sont les mêmes.

Ces valeurs sont également calculées par les résistances de connexion et les sources sur la planche à pain. Et nous pouvons mesurer la tension et le courant traversant toutes les branches à l'aide d'un voltmètre et d'un ampèremètre.

Par conséquent, il est prouvé le théorème de Tellegen.

• Article connexe :Loi de courant et de tension de Kirchhoff (KCL et KVL) | Exemple résolu

Application du théorème de Tellegen

Ce théorème est très fondamental et largement utilisé dans l'analyse des circuits. Il existe de nombreuses applications de ce théorème. Certaines applications sont répertoriées ci-dessous.

• Pour la conception des filtres, ce théorème est très utile dans les applications de traitement numérique du signal.
• Pour déterminer la stabilité des usines chimiques, ce théorème est utilisé en génie chimique.
• Ce théorème s'applique au système localisé ayant des éléments linéaires-non linéaires, actifs-passifs, variables dans le temps/invariants dans le temps.
• Ce théorème est utilisé dans le processus biologique.
• Il est utilisé dans la topologie et l'analyse de la réaction de la structure.
• Il est également utilisé pour trouver le comportement dynamique du réseau physique.

Tutoriels d'analyse de circuit électrique associés :

• Théorème de superposition – Analyse de circuit avec exemple résolu
• Calculateur de règles de Cramer – Système d'équations à 2 et 3 équations pour les circuits électriques
• Pont de Wheatstone – Circuit, fonctionnement, dérivation et applications
• Calculatrices d'ingénierie électrique et électronique
• Plus de 5 000 formules et équations d'ingénierie électrique et électronique