Théorème de superposition - Analyse de circuit avec exemple résolu

Théorème de superposition - Guide étape par étape avec exemple résolu

Qu'est-ce que le théorème de superposition ?

Le théorème de superposition est utilisé pour résoudre des réseaux complexes avec un certain nombre de sources d'énergie. C'est un concept important pour déterminer la tension et le courant à travers les éléments en calculant l'effet de chaque source individuellement. Et combinez l'effet de toutes les sources pour obtenir la tension et le courant réels de l'élément de circuit.

Le théorème de superposition stipule que ;

En d'autres termes, nous ne considérerons qu'une seule source indépendante agissant à la fois. Nous devons donc supprimer d'autres sources. Les sources de tension sont court-circuitées et les sources de courant sont en circuit ouvert pour des sources idéales. Si la résistance interne des sources est donnée, vous devez considérer le circuit.

Le théorème de superposition ne s'applique qu'au circuit qui suit la loi d'Ohm.

• Article connexe : Théorème de Thevenin. Guide étape par étape avec exemple résolu

Quand utiliser le théorème de superposition ?

Le réseau doit respecter les exigences ci-dessous pour appliquer le théorème de superposition.

• Les composants utilisés dans le circuit doivent être linéaires. Cela signifie, pour les résistances, que le flux de courant est proportionnel à la tension ; pour les inducteurs, la liaison de flux est proportionnelle au courant. Par conséquent, la résistance, l'inductance et le condensateur sont des éléments linéaires. Mais la diode, le transistor n'est pas un élément linéaire.
• Les composants du circuit doivent être des éléments bilatéraux. Cela signifie que l'amplitude du courant est indépendante de la polarité des sources d'énergie.
• A l'aide du théorème de superposition, nous pouvons trouver le courant qui traverse un élément, la chute de tension de la résistance et la tension du nœud. Mais nous ne pouvons pas trouver la puissance dissipée de l'élément.

• Article connexe : Théorème de Norton. Guide étape par étape avec exemple résolu

Étapes à suivre pour le théorème de superposition

Étape 1 Découvrez un certain nombre de sources indépendantes disponibles dans le réseau.

Étape 2 Choisissez une source et éliminez toutes les autres sources. Si le réseau se compose d'une source dépendante, vous ne pouvez pas l'éliminer. Il reste tel quel tout au long du calcul.

Si vous considérez que toutes les sources d'énergie sont des sources idéales, vous n'avez pas besoin de tenir compte de la résistance interne. Et directement la source de tension de court-circuit et la source de courant en circuit ouvert. Mais au cas où, si la résistance interne des sources est donnée, vous devez remplacer la résistance interne.

Étape 3 Or, dans un circuit, une seule source d'énergie indépendante est présente. Vous devez trouver une réponse avec une seule source d'énergie dans le circuit.

Étape 4 Répétez les étapes 2 et 3 pour toutes les sources d'énergie disponibles sur le réseau. S'il y a trois sources indépendantes, vous devez répéter ces étapes trois fois. Et chaque fois que vous obtenez une valeur de la réponse.

Étape 5 Maintenant, combinez toutes les réponses par sommation algébrique obtenue par des sources individuelles. Et vous obtiendrez une valeur finale de réponse pour un élément particulier d'un réseau. Si vous avez besoin de trouver une réponse pour d'autres éléments, vous devez suivre à nouveau ces étapes pour cet élément.

• Article connexe :  Analyse de circuit SUPERMESH – Étape par étape avec exemple résolu

Exemple de résolution du théorème de superposition

Exemple :

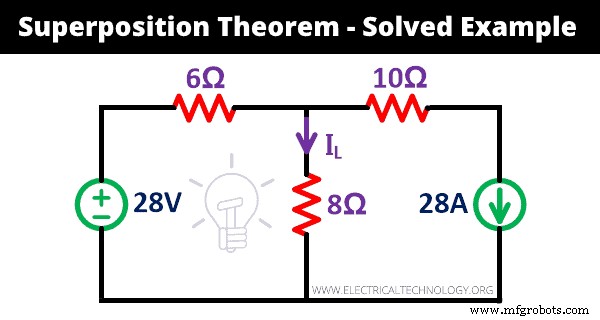
Comprenons le fonctionnement du théorème de superposition par exemple. Trouver le courant (I_L ) passe à travers la résistance 8Ω dans le réseau donné en utilisant le théorème de superposition.

Solution :

Étape 1 Comme indiqué dans le réseau ci-dessus, une source de tension et une source de courant sont données. Par conséquent, nous devons répéter la procédure deux fois.

Étape 2 Nous considérons d'abord que la source de tension 28V est présente dans le réseau. Donc, vous devez supprimer la source de courant par des bornes en circuit ouvert. Comme ici, nous considérons la source de courant comme une source de courant idéale. Donc, nous n'avons pas besoin de connecter la résistance interne.

Le circuit restant est comme indiqué dans la figure ci-dessous.

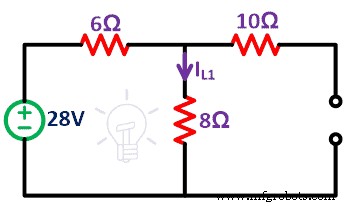
Étape 3 Trouver le courant (I_L1 ) passe à travers une résistance de 8Ω. Il donne uniquement l'effet d'une source de tension.

En raison du circuit ouvert d'une source de courant, aucun courant ne traverse la résistance de 10 Ω. Ainsi, le réseau se compose d'une seule boucle.

Appliquer KVL à la boucle ;

28 =6je _{L 1} + 8je _{L 1}

28 =14je _{L 1}

Je _{L 1} =28/14

Je _{L 1} =2A

Étape 4 Maintenant, nous répétons la même procédure pour la source actuelle. Dans cette condition, nous supprimons la source de tension en court-circuitant. Un circuit restant est comme indiqué dans la figure ci-dessous.

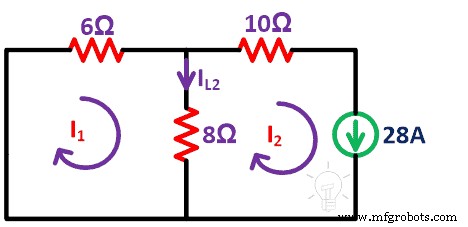
Ici, nous devons considérer deux boucles. Je₁ et moi₂ sont en courant de boucle. Et trouvez le courant I_L2 .

Appliquer KVL à la boucle-1 ;

0 =6je ₁ + 8je ₁ – 8je ₂

14je ₁ – 8je ₂ =0

Le courant qui traverse la boucle-2 est calculé à partir de la source de courant. Et ce sera;

Je ₂ =28A

Mettez cette valeur dans l'équation ci-dessus ;

14je ₁ – 8 (28) =0

Je ₁ =16A

Maintenant, la branche de résistance 8Ω est commune dans les deux boucles. Donc, nous devons trouver le courant résultant (I_L2 ) passe à travers la résistance 8Ω.

Je _{L 2} =je ₁ – je ₂

Je _{L 2} =16 – 28

Je _{L 2} =-12A

Étape 5 Maintenant, nous combinons l'effet des deux sources par sommation algébrique du courant. Ainsi, le courant total qui traverse la résistance de 8Ω est I_L . Ici, le sens du courant est le plus important. Courant I_L2 a un signe moins. Cela signifie que pendant la source 28A, le courant circule dans le sens opposé. Et nous ne pouvons pas changer de direction. C'est la raison pour laquelle, en combinant toutes les sources, nous faisons une sommation algébrique.

Je _L =Je_{L 1} – Je_{L 2}

Je _L =2 + (-12)

Je _L =-10A

Ici, nous avons supposé que le courant qui traverse la résistance de 8 Ω est dans le sens de la flèche indiquée sur la figure. Le signe moins indique la direction opposée. Et la quantité de courant est de 8A.

• Article connexe :Analyse de circuit SUPERNODE – Étape par étape avec exemple résolu

Expérience du théorème de superposition

L'expérience du théorème de superposition peut être effectuée en suivant les étapes ci-dessous.

Visez

Déterminer le courant traversant les résistances et vérifier le théorème de superposition.

Composants requis

Source CC, résistances, multimètres CC, fils de connexion, planche à pain, etc.

Théorie

Le théorème de superposition est utilisé dans l'analyse de circuit pour trouver le courant et la tension aux bornes des éléments d'un circuit donné. Ce théorème est utile lorsque le nombre de sources est supérieur.

Selon le théorème de superposition, la réponse des éléments est une somme algébrique de la réponse des sources d'énergie individuelles.

Tout d'abord, nous allons calculer le courant qui traverse les résistances dans un réseau donné. Lorsque toutes les sources sont connectées. Après cela, nous supprimons les sources et trouvons des courants pour des sources individuelles. Enfin, la somme des courants mesurés à partir des sources individuelles est similaire aux mesures de courant avec toutes les sources connectées.

Procédure

Nous considérons le circuit bilatéral linéaire donné dans la figure ci-dessous.

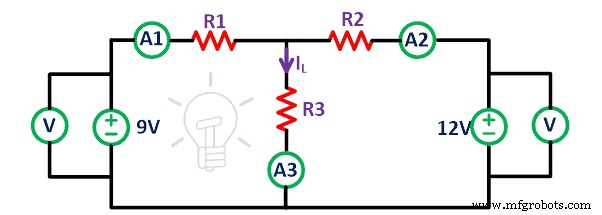
Connectez tous les éléments sur la planche à pain comme indiqué dans le circuit ci-dessus à l'aide de fils de connexion. Connectez un ampèremètre à toutes les résistances pour trouver le courant qui traverse les résistances. Ici, nous avons deux sources de tension.

Dans le premier cas, mesurez le courant qui traverse toutes les résistances lorsque les deux sources de tension sont présentes dans le circuit. Le courant traversant la résistance R₁ , R₂ , et R₃ est je ₁ , je ₂ , et je ₃ respectivement.

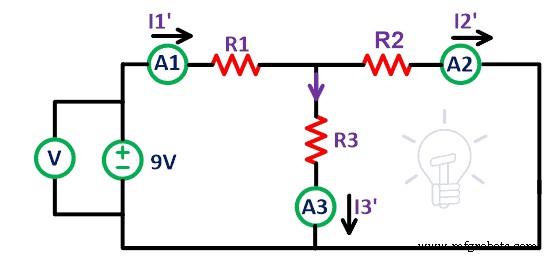
Retirez maintenant la source de tension 12 V du circuit. Court-circuitez les bornes A' et B' comme indiqué sur la figure ci-dessus. Ici, nous avons supposé que les sources de tension sont idéales. Donc, pas besoin de connecter une résistance interne. Maintenant, mesurez le courant I _1′ , je _2′ et je _3′ qui est le courant qui traverse respectivement la résistance R1, R2 et R3.

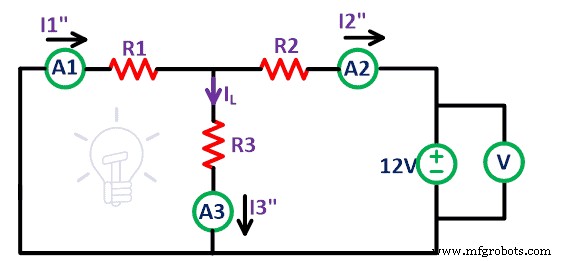
De même, retirez la source de tension 9 V et le circuit restant est comme indiqué dans la figure ci-dessus. Encore une fois, mesurez le courant traversant toutes les résistances et nommez-le I _{1 "} , je _{2 "} , et je _{3 "} .

• Message connexe : Théorème de transfert de puissance maximale pour les circuits CA et CC

Placez toutes les valeurs dans le tableau d'observation ci-dessous.

Tableau d'observation

Connexion source	R1	R2	R3
Les deux sources sont connectées	je 1	je 2	je 3
Seul le 12 V est connecté	je 1′	je 2′	je 3′
Seul le 9V est connecté	je 1″	je 2″	je 3″

Calcul :

Je ₁ =je _1′ + je _1″

Je ₂ =je _2′ + je _2″

Je ₃ =je _3′ + je _3″

Pour vérifier le théorème de superposition, nous comparons la somme algébrique des passages de courant à travers les résistances lorsqu'une source individuelle est connectée avec le courant mesuré lorsque les deux sources sont connectées dans un circuit.

Si le calcul ci-dessus est satisfaisant, nous pouvons prouver le théorème de superposition.

Conclusion

Dans cette expérience, nous pouvons prouver que le courant qui traverse la résistance est une somme algébrique du courant lorsqu'une source d'énergie individuelle est connectée. Et cela prouve le théorème de superposition.

• Article connexe :Loi de courant et de tension de Kirchhoff (KCL et KVL) | Exemple résolu

Application du théorème de superposition

• Le théorème de superposition peut être utilisé pour les réseaux AC et DC.
• Lorsque le nombre de sources indépendantes est plus important, il est facile de trouver une réponse du réseau.
• Il aide à calculer les passages de courant et la tension aux bornes de l'élément en calculant l'effet de chaque source d'énergie individuellement. Et après, nous pourrons déterminer l'effet combiné sur les éléments de toutes les sources.

Inconvénient du théorème de superposition

• Le théorème de superposition ne peut pas s'appliquer au circuit n'ayant qu'une source dépendante. Il fallait au moins deux sources indépendantes.
• Ce théorème ne s'applique qu'au réseau constitué d'éléments linéaires. Il ne peut pas s'appliquer aux éléments non linéaires comme une diode, un transistor, etc.
• Nous ne pouvons pas calculer la puissance par ce théorème. Comme la puissance est proportionnelle au carré de la tension et du courant, elle devient non linéaire.
• Ce théorème n'est pas applicable dans une condition où la résistance varie avec la tension et le courant. Pour toutes les sources d'énergie, la valeur de la résistance doit rester constante.
• Ce théorème ne s'applique qu'aux éléments bilatéraux. Si la réponse du réseau dépend du sens du courant, ce théorème n'est pas applicable.

Tutoriels d'analyse de circuit électrique associés :

• Théorème de Tellegen – Exemples résolus et simulation MATLAB
• Calculateur de règles de Cramer – Système d'équations à 2 et 3 équations pour les circuits électriques
• Pont de Wheatstone – Circuit, fonctionnement, dérivation et applications
• Calculatrices d'ingénierie électrique et électronique
• Plus de 5 000 formules et équations d'ingénierie électrique et électronique