Théorème de Millman - Analyse des circuits AC et DC - Exemples

Théorème de Millman pour les circuits AC et DC - Exemples résolus étape par étape

Théorème de Millman

Le théorème de Millman est utilisé dans l'analyse de circuit lorsqu'il n'a que des branches en parallèle. Par conséquent, ce théorème est utile pour calculer la tension à la fin d'un circuit. Le théorème de Millman n'est applicable qu'au circuit qui contient un réseau parallèle.

Le théorème de Millman est une combinaison du théorème de Thevenin et le théorème de Norton . Parfois, ce théorème est également appelé théorème du générateur parallèle . Ce théorème est proposé par le professeur de génie électrique Jacob Millman . Et d'après son nom, ce théorème est nommé théorème de Millman.

Le théorème de Millman stipule que ;

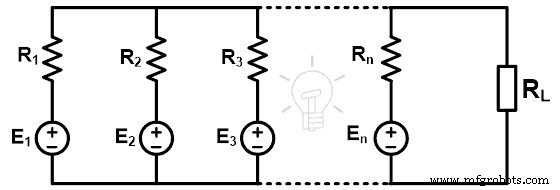
Cela signifie que nous pouvons trouver la tension aux bornes des branches parallèles du réseau donné. Ce théorème réduit la complexité du réseau lorsque plusieurs sources sont connectées comme le montre la figure ci-dessous.

Selon le théorème de Millman ; la tension aux bornes de la charge est ;

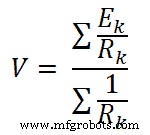
• Article connexe : Théorème de Thevenin. Guide étape par étape avec exemple résolu

Équation mathématique

Comme le montre la figure ci-dessus, le circuit ayant un nombre n de sources de tension (E₁ , E₂ , E₃ , …, E_n ). Et la résistance interne des sources est R₁ , R₂ , R₃ , …, R_n respectivement. Selon le théorème de Millman, tout circuit peut être remplacé par le réseau ci-dessous. La figure suivante montre le circuit équivalent de Millman.

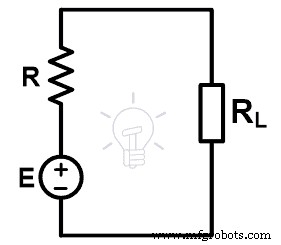
Maintenant, nous devons trouver la valeur de la source de tension (E) et la résistance équivalente (R). Le circuit ci-dessus est similaire au circuit équivalent de Thevenin. Par conséquent, nous pouvons dire que la source de tension (E) est la même que la tension équivalente de Thevenin (V_TH ) et la résistance équivalente est la résistance équivalente de Thevenin (R_TH ).

Nous trouvons le circuit équivalent de Norton pour faire un calcul facile. Pour cela, nous allons faire une transformation de source. Et convertissez toutes les sources de tension en sources de courant.

Nous avons une résistance interne connectée en série avec la source de tension. Après transformation de la source, la source de tension est convertie en source de courant et la résistance interne est connectée en parallèle avec la source de courant. Par conséquent, le circuit ci-dessus est converti comme indiqué dans la figure ci-dessous.

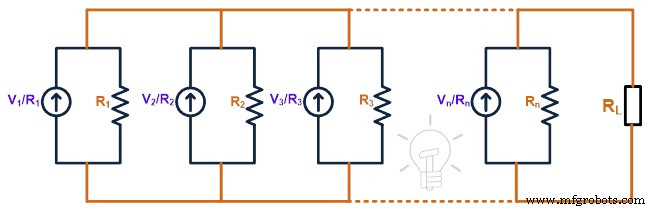
Selon la loi d'ohm, la valeur des sources de courant sera E₁ /R₁ , E₂ /R₂ , E₃ /R₃ , …, E_n /R_n . Maintenant, pour trouver le courant équivalent de Norton (I_N ), nous devons court-circuiter les bornes de charge. Et trouvez le courant passe par cette branche.

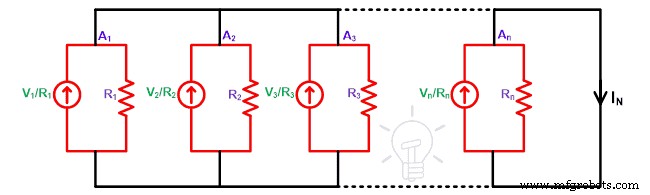
Au nœud A₁ , le courant se divise en deux chemins. Un chemin passe par la résistance R₁ et le deuxième chemin part de la branche court-circuitée. Comme nous le savons, le courant passe toujours par le chemin à faible résistance. Par conséquent, dans cet état, tout le courant passe par la branche court-circuitée. Et le courant qui traverse la résistance est nul.

Cette même chose se produit pour toutes les sources au nœud A₂ , A₃ , …, A_n . Et le courant qui traverse toutes les résistances est nul.

Maintenant, au nœud A₂ , le courant provenant du nœud A₁ est ajouté. De même, au nœud A3, le courant provenant du nœud A₂ est ajouté. Par conséquent, au nœud A_n , courant de tous les nœuds ajoutés. Le courant total est une somme de tous les courants et il est connu sous le nom de courant de Norton (I_N ).

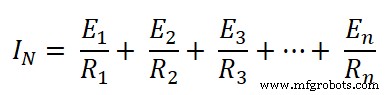
Ainsi, nous avons trouvé le courant équivalent de Norton. Maintenant, nous devons trouver la résistance équivalente de Norton. Et pour cela, nous devons supprimer toutes les sources d'énergie présentes dans le circuit en ouvrant le circuit de la source de courant et en court-circuitant la source de tension.

Dans la figure ci-dessus, nous n'avons qu'une source actuelle. Nous supprimerons ces sources de courant en circuit ouvert. Et nous devons supprimer la charge pour calculer la résistance équivalente. Par conséquent, le circuit restant ressemble à la figure ci-dessous.

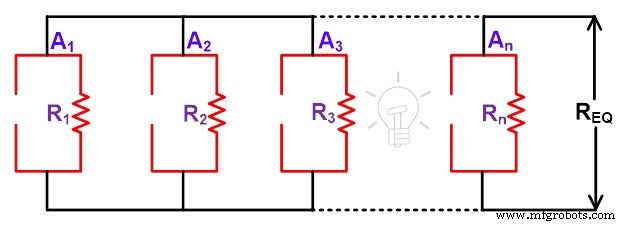
Comme le montre la figure ci-dessus, nous pouvons voir que tous les résistants sont connectés en parallèle. Et cette combinaison parallèle est égale à la résistance équivalente.

R_eq =R_N =R ₁ || R ₂ || R ₃ … || R_n

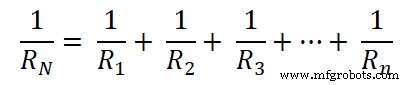
Maintenant, placez ces valeurs dans le circuit équivalent de Norton, comme indiqué dans la figure ci-dessous.

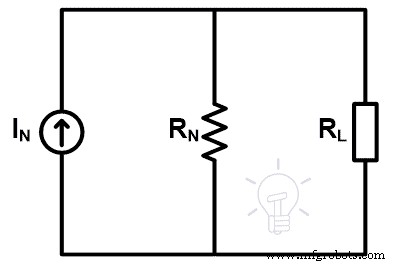
Si nous convertissons ce circuit équivalent de Norton en circuit équivalent de Thevenin, nous pouvons calculer la valeur de E et R à partir du courant de Norton I_N et résistance Norton R_N .

Selon la loi d'Ohm ;

E =I_N x R_N

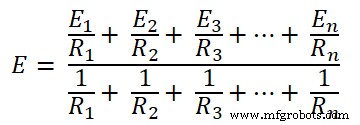
Faisons l'équation ci-dessus sous une forme générale pour n-nombre de branches.

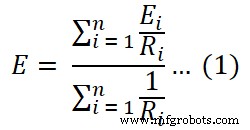
Ainsi, nous avons la valeur de la source de tension. Et la valeur de la résistance équivalente est égale à la résistance équivalente de Norton. Par conséquent, nous pouvons obtenir le circuit équivalent de Millman (fig-2).

• Article connexe : Théorème de Norton. Guide étape par étape avec exemple résolu

Étapes à suivre pour le théorème de Millman

Étape 1 Le théorème de Milliman est le seul applicable au réseau ou circuit ayant le plus grand nombre de branches parallèles. Donc, nous supposons que nous devons résoudre le circuit avec un certain nombre de branches parallèles contenant une source de tension connectée en série avec la résistance interne.

Étape 2 Faites une liste de la résistance interne ou de la résistance connectée en série et des sources de tension.

Étape 3 Trouvez la résistance équivalente (R) aux bornes de la charge en court-circuitant les sources de tension.

Étape 4 Appliquez le théorème de Millman et trouvez la valeur de la tension (E) aux bornes de la charge. Pour cela, utilisez l'équation-1. Cette tension est la tension aux bornes de la charge.

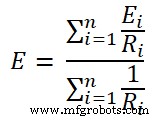
Étape 5 Mettez la valeur de R et E dans le circuit équivalent de Millman (fig-2).

Étape 6 Appliquez KVL à la boucle pour trouver le courant qui traverse la charge.

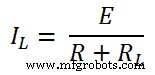
• Article connexe : Théorème de superposition – Analyse de circuit avec exemple résolu

Analyse d'un circuit CC à l'aide du théorème de Millman

Exemple #1

Trouvez le courant et la tension aux bornes de la borne de charge à l'aide du théorème de Millman.

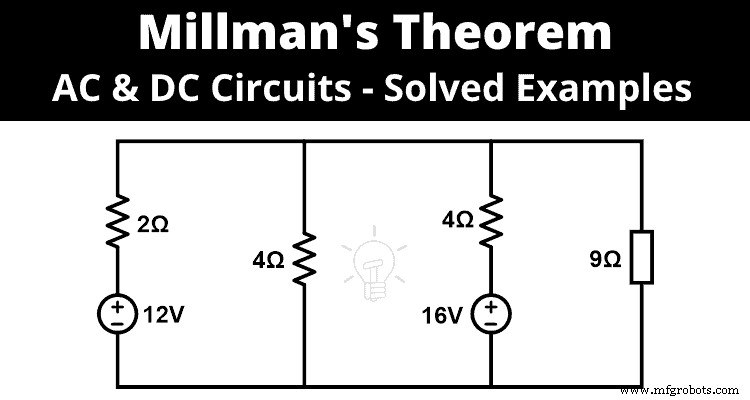
Étape 1 En observant la figure ci-dessus, on peut dire que les quatre branches sont connectées en parallèle. Et nous pouvons appliquer le théorème de Millman.

Étape 2 Il y a trois branches à l'exception de la branche de charge. Donc, il y a trois tensions et trois résistances comme indiqué ci-dessous.

E ₁ =12V et R ₁ =2Ω

E ₂ =0V et R ₁ =4Ω

E ₃ =16V et R ₁ =4Ω

Étape 3 Pour trouver la résistance équivalente, il faut supprimer les sources de tension par court-circuit et ouvrir les bornes de charge. Par conséquent, le chiffre restant est indiqué dans la figure ci-dessous.

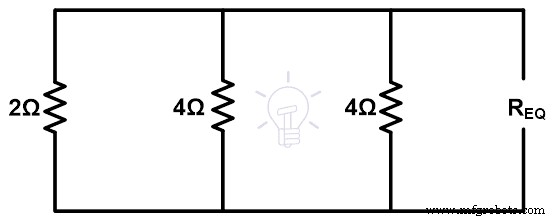
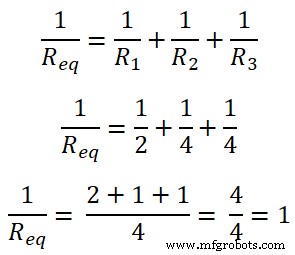
R_eq =1Ω

Comme le montre la figure ci-dessus, toutes les résistances sont en parallèle. Ainsi, la résistance équivalente est ;

Étape 4 Maintenant, appliquez le théorème de Millman.

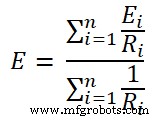
Dans cet exemple, nous avons 3 branches. Par conséquent, nous utilisons n=3.

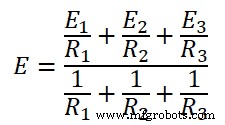
Mettre les valeurs énumérées ci-dessus dans cette équation.

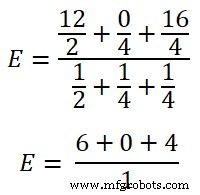
E =10V

Il s'agit de la tension aux bornes de la charge.

Étape 5 Mettez ces valeurs dans le circuit équivalent de Millman.

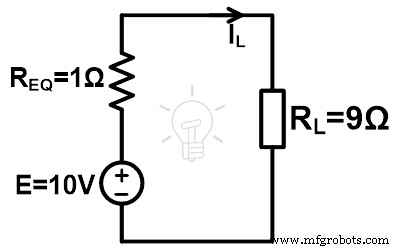
Étape 6 Selon la loi d'ohm,

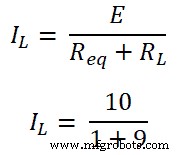
I_L =1A

Par conséquent, la tension aux bornes de la charge est de 10 V et le courant qui traverse la charge est de 1 A.

• Article connexe : Théorème de Tellegen – Exemples résolus et simulation MATLAB

Analyse d'un circuit CA à l'aide du théorème de Millman

Exemple #2

Trouvez le courant et la tension aux bornes de la charge à l'aide du théorème de Millman.

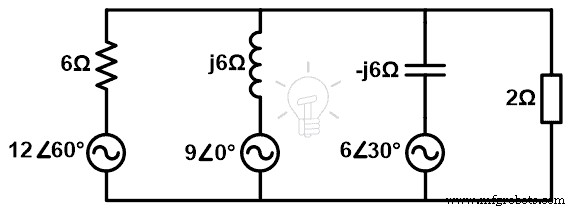
Étape 1 Comme le montre la figure ci-dessus, quatre branches sont connectées en parallèle. Par conséquent, nous pouvons appliquer le théorème de Millman.

Étape 2 Si l'on ne considère pas la branche de charge, il y a trois branches. Pour faciliter le calcul, nous énumérerons les tensions et l'impédance. Dans le cas d'un circuit alternatif, nous devons utiliser le mot impédance au lieu de résistance.

Les valeurs des sources de tension sont données sous forme polaire. Mais, les valeurs des impédances sont données sous la forme rectangulaire. Nous devons donc convertir les valeurs de la source de tension sous forme polaire.

V ₁ =12∠60° =6 + j 10.392

V ₂ =9∠0° =9 + j 0

V ₃ =6∠30° =5,196 + j 3

Les impédances sont données sous forme rectangulaire. Donc, nous le listons tel quel.

Z ₁ =6Ω

Z ₂ =j 6Ω

Z ₃ =–j 6Ω

Étape 3 Trouvez l'impédance équivalente. Comme le montre l'exemple ci-dessus, nous devons supprimer toutes les sources de tension par court-circuit. Et le circuit restant est comme indiqué dans la figure ci-dessous.

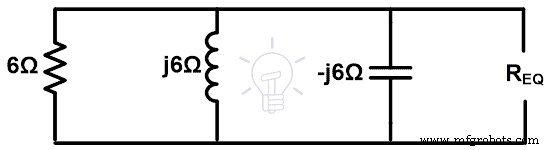
Ici, toutes les impédances sont connectées en parallèle. Ainsi, l'impédance équivalente sera ;

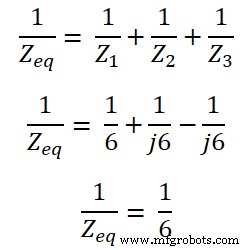
Z _équip =6Ω

Étape 4 Maintenant, appliquez le théorème de Milliman,

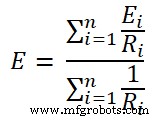
Ici, nous avons trois branches. Par conséquent, n est égal à 3.

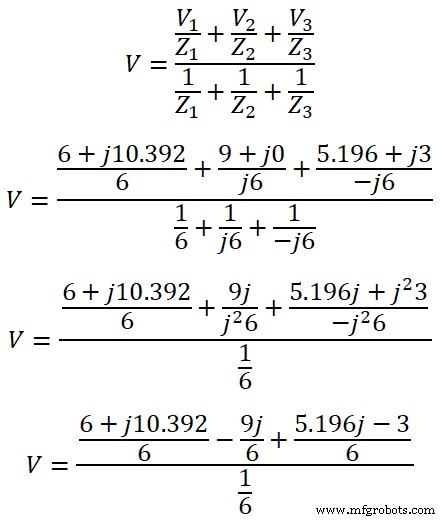
V =6 + 1j 0,392 – j 9 + j 5.196 – 3

V =3 + j 6.588

Maintenant, nous devons trouver la valeur RMS.

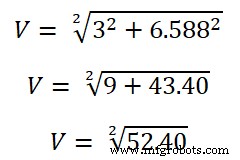
V =7.23V

Étape 5 Mettez ces valeurs dans le circuit équivalent de Millman.

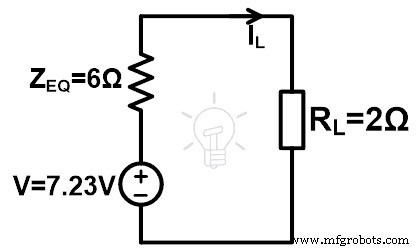
Étape 6 Selon la loi d'ohm,

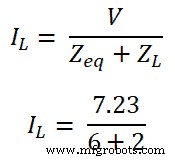
I_L =0.9A

• Message connexe : Théorème de transfert de puissance maximale pour les circuits CA et CC
  

Limitation du théorème de Millman

Le théorème de Millman est très utile pour résoudre le réseau. Mais il y a une limitation qui est listée ci-dessous.

• Ce théorème ne s'applique pas au circuit ayant une source dépendante entre la source indépendante.
• Pour le circuit ayant moins de deux sources indépendantes, ce théorème n'est pas utile.
• Ce théorème ne s'applique pas au circuit n'ayant que des éléments en série.
• Lorsqu'il y a un élément connecté entre la source, ce théorème ne peut pas être applicable.

Applications du théorème de Millman

Le théorème de Millman est largement utilisé dans l'analyse de réseau pour résoudre les circuits complexes. L'application du théorème de Millman est indiquée ci-dessous.

• Le théorème de Millman est le plus utile pour trouver la tension et le courant d'impédance de charge dans le cas où un plus grand nombre de branches parallèles sont disponibles avec un certain nombre de sources de tension.
• Le calcul de ce théorème est facile. Il ne nécessite pas l'utilisation de plus d'équations.
• Ce théorème est utilisé pour résoudre le circuit complexe ayant des éléments complexes comme Op-Amp.

Tutoriels d'analyse de circuit électrique associés :

• Analyse de circuit SUPERNODE – Étape par étape avec exemple résolu
• Analyse de circuit SUPERMESH - étape par étape avec exemple résolu
• Loi du courant et de la tension de Kirchhoff (KCL et KVL) | Exemple résolu
• Calculateur de règles de Cramer – Système d'équations à 2 et 3 équations pour les circuits électriques
• Pont de Wheatstone – Circuit, fonctionnement, dérivation et applications
• Calculatrices d'ingénierie électrique et électronique
• Plus de 5 000 formules et équations d'ingénierie électrique et électronique