Circuits de condensateur AC

Condensateurs vs. Résistances

Les condensateurs ne se comportent pas de la même manière que les résistances. Alors que les résistances permettent un flux d'électrons à travers elles directement proportionnel à la chute de tension, les condensateurs s'opposent aux changements en tension en tirant ou en fournissant du courant lorsqu'ils se chargent ou se déchargent jusqu'au nouveau niveau de tension.

Le flux d'électrons "à travers" un condensateur est directement proportionnel au taux de changement de tension aux bornes du condensateur. Cette opposition au changement de tension est une autre forme de réactance , mais qui est précisément à l'opposé de celui présenté par les inducteurs.

Caractéristiques du circuit de condensateur

Exprimée mathématiquement, la relation entre le courant "à travers" le condensateur et le taux de variation de tension à travers le condensateur est la suivante :

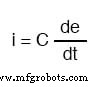
L'expression de/dt est l'un des calculs, c'est-à-dire le taux de variation de la tension instantanée (e) au fil du temps, en volts par seconde. La capacité (C) est en Farads, et le courant instantané (i), bien sûr, est en ampères.

Parfois, vous trouverez le taux de changement de tension instantané au fil du temps exprimé en dv/dt au lieu de de/dt :en utilisant la lettre minuscule « v » à la place ou « e » pour représenter la tension, mais cela signifie exactement la même chose. Pour montrer ce qui se passe avec le courant alternatif, analysons un simple circuit de condensateur :

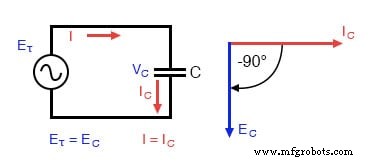
Circuit capacitif pur :la tension du condensateur est en retard de 90° sur le courant du condensateur

Si nous devions tracer le courant et la tension pour ce circuit très simple, cela ressemblerait à ceci :

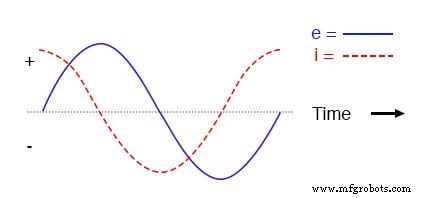
Formes d'onde de circuit capacitif pur.

N'oubliez pas que le courant traversant un condensateur est une réaction contre le changement en tension à ses bornes.

Par conséquent, le courant instantané est nul chaque fois que la tension instantanée est à un pic (changement nul, ou pente de niveau, sur l'onde sinusoïdale de tension), et le courant instantané est à un pic partout où la tension instantanée est au changement maximum (les points de pente la plus raide sur l'onde de tension, là où elle croise la ligne zéro).

Il en résulte une onde de tension déphasée de -90° par rapport à l'onde de courant. En regardant le graphique, l'onde de courant semble avoir une « longueur d'avance » sur l'onde de tension; le courant « devance » la tension et la tension « est en retard » par rapport au courant.

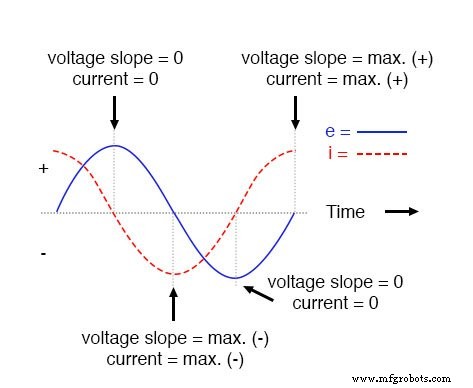
La tension est en retard de 90° sur le courant dans un circuit capacitif pur.

Comme vous l'avez peut-être deviné, la même onde de puissance inhabituelle que nous avons vue avec le circuit à inducteur simple est également présente dans le circuit à condensateur simple :

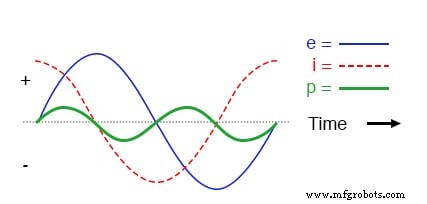
Dans un circuit capacitif pur, la puissance instantanée peut être positive ou négative.

Comme avec le circuit inducteur simple, le déphasage de 90 degrés entre la tension et le courant entraîne une onde de puissance qui alterne également entre positif et négatif. Cela signifie qu'un condensateur ne dissipe pas de puissance lorsqu'il réagit aux changements de tension; il absorbe et libère simplement de la puissance, alternativement.

Réactance d'un condensateur

L'opposition d'un condensateur au changement de tension se traduit par une opposition à la tension alternative en général, qui par définition change toujours en amplitude et en direction instantanées.

Pour une amplitude donnée de tension alternative à une fréquence donnée, un condensateur de taille donnée « conduira » une certaine amplitude de courant alternatif.

Tout comme le courant à travers une résistance est fonction de la tension aux bornes de la résistance et de la résistance offerte par la résistance, le courant alternatif à travers un condensateur est fonction de la tension alternative à ses bornes et de la réactance offert par le condensateur.

Comme pour les inductances, la réactance d'un condensateur est exprimée en ohms et symbolisée par la lettre X (ou XC pour être plus précis).

Étant donné que les condensateurs « conduisent » le courant proportionnellement au taux de changement de tension, ils laisseront passer plus de courant pour des tensions changeant plus rapidement (car ils se chargent et se déchargent aux mêmes pics de tension en moins de temps) et moins de courant pour des tensions changeant plus lentement.

Cela signifie que la réactance en ohms pour tout condensateur est inversement proportionnel à la fréquence du courant alternatif.

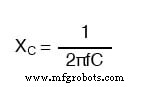
Réactance d'un condensateur de 100 uF :

Fréquence (Hertz) Réactance (Ohms) 6026.525812013.262925000.6366

Veuillez noter que la relation entre la réactance capacitive et la fréquence est exactement opposée à celle de la réactance inductive.

La réactance capacitive (en ohms) diminue avec l'augmentation de la fréquence alternative. Inversement, la réactance inductive (en ohms) augmente avec l'augmentation de la fréquence alternative. Les inductances s'opposent à des courants changeant plus rapidement en produisant des chutes de tension plus importantes ; les condensateurs s'opposent à des chutes de tension changeantes plus rapides en permettant des courants plus importants.

Comme pour les inducteurs, le terme 2πf de l'équation de réactance peut être remplacé par la lettre grecque minuscule Omega (ω), qui est appelée la vitesse angulaire du circuit alternatif. Ainsi, l'équation XC =1/(2πfC) pourrait également être écrite sous la forme XC =1/(ωC), avec ω exprimé en unités de radians par seconde .

Le courant alternatif dans un circuit capacitif simple est égal à la tension (en volts) divisée par la réactance capacitive (en ohms), tout comme le courant alternatif ou continu dans un circuit résistif simple est égal à la tension (en volts) divisée par le résistance (en ohms). Le circuit suivant illustre cette relation mathématique par l'exemple :

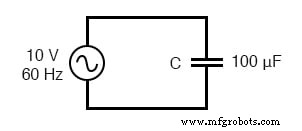
Réactance capacitive.

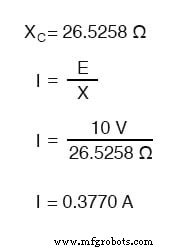
Cependant, nous devons garder à l'esprit que la tension et le courant ne sont pas en phase ici. Comme cela a été montré précédemment, le courant a un déphasage de +90° par rapport à la tension. Si nous représentons mathématiquement ces angles de phase de tension et de courant, nous pouvons calculer l'angle de phase de l'opposition réactive du condensateur au courant.

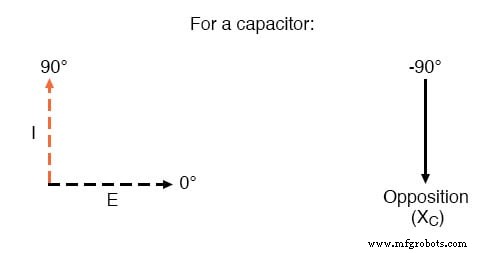
La tension retarde le courant de 90° dans un condensateur.

Mathématiquement, nous disons que l'angle de phase de l'opposition d'un condensateur au courant est de -90°, ce qui signifie que l'opposition d'un condensateur au courant est une quantité imaginaire négative. (Voir la figure ci-dessus.) Cet angle de phase d'opposition réactive au courant devient d'une importance critique dans l'analyse des circuits, en particulier pour les circuits CA complexes où la réactance et la résistance interagissent.

Il s'avérera avantageux de représenter tout l'opposition du composant au courant en termes de nombres complexes, et pas seulement de quantités scalaires de résistance et de réactance.

AVIS :

• Réactance capacitive est l'opposition qu'offre un condensateur au courant alternatif en raison de son stockage déphasé et de sa libération d'énergie dans son champ électrique. La réactance est symbolisée par la lettre majuscule « X » et est mesurée en ohms tout comme la résistance (R).
• La réactance capacitive peut être calculée à l'aide de cette formule :XC =1/(2πfC)
• La réactance capacitive diminue avec une fréquence croissante. Autrement dit, plus la fréquence est élevée, moins elle s'oppose (plus elle « conduit ») au courant alternatif.

FICHES DE TRAVAIL CONNEXES :

• Fiche de travail sur les condensateurs