Impédance caractéristique

Les fils parallèles de longueur infinie

Supposons, cependant, que nous ayons un ensemble de fils parallèles infinis longueur, sans lampe au bout. Que se passerait-il lorsque nous fermions l'interrupteur ? Etant donné qu'il n'y a plus de charge au bout des fils, ce circuit est ouvert. N'y aurait-il pas du tout de courant ? (Figure ci-dessous)

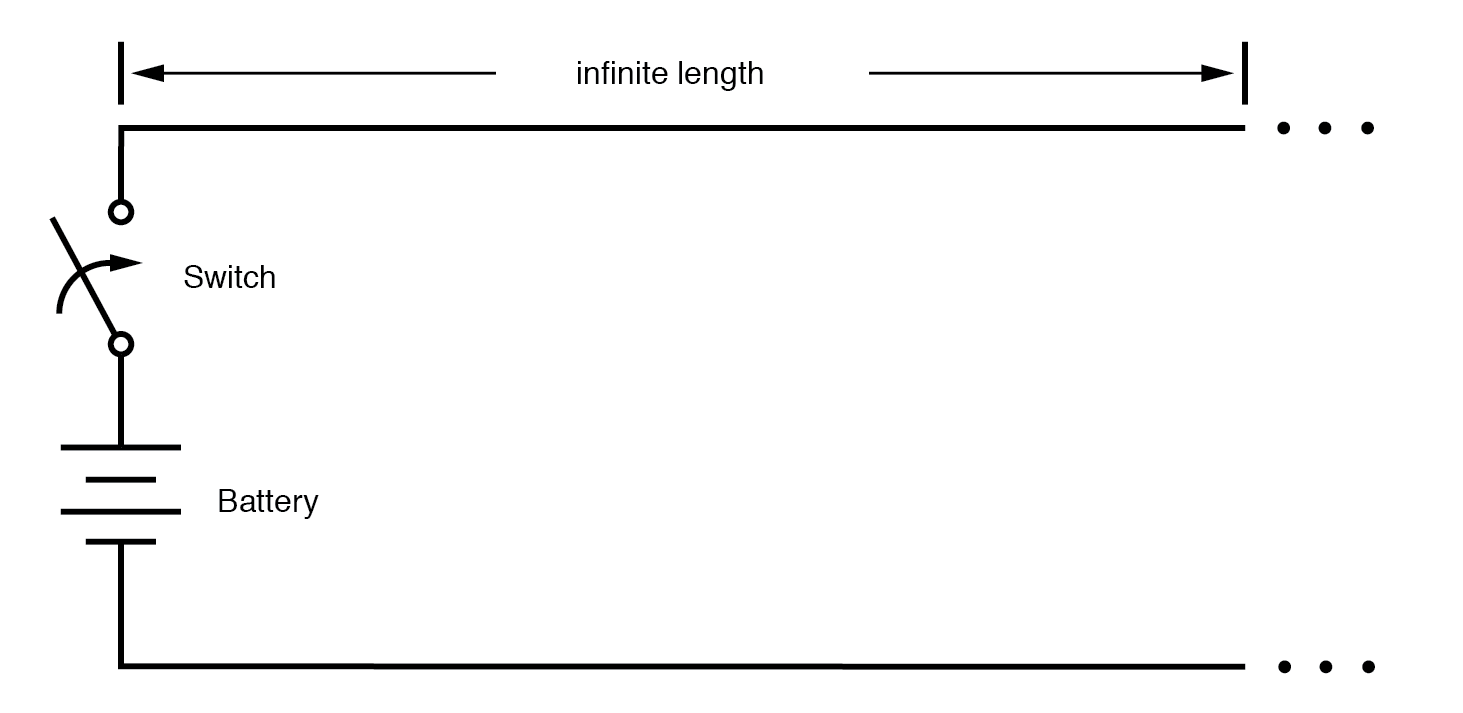
Conduire une ligne de transmission infinie.

Bien qu'il soit possible d'éviter la résistance des fils grâce à l'utilisation de supraconducteurs dans cette « expérience de pensée », nous ne pouvons pas éliminer la capacité le long des longueurs des fils. Tout paire de conducteurs séparés par un milieu isolant crée une capacité entre ces conducteurs :(Figure ci-dessous)

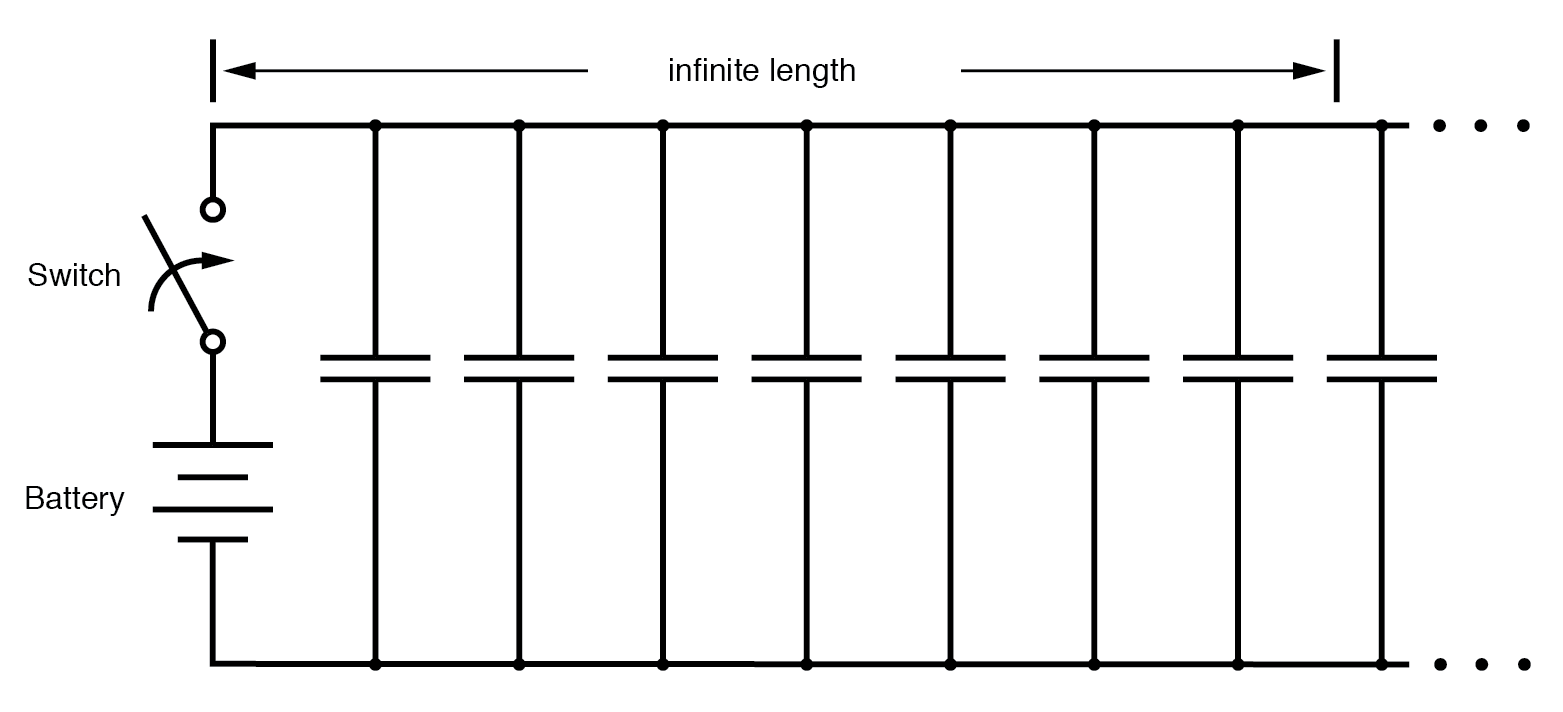
Circuit équivalent montrant la capacité parasite entre les conducteurs.

La tension appliquée entre deux conducteurs crée un champ électrique entre ces conducteurs. L'énergie est stockée dans ce champ électrique, et ce stockage d'énergie se traduit par une opposition au changement de tension. La réaction d'une capacité contre les variations de tension est décrite par l'équation i =C(de/dt), qui nous indique que le courant sera tiré proportionnellement au taux de variation de la tension au fil du temps. Ainsi, lorsque l'interrupteur est fermé, la capacité entre les conducteurs réagira contre l'augmentation soudaine de la tension en chargeant et en tirant du courant de la source. Selon l'équation, une augmentation instantanée de la tension appliquée (comme produite par la fermeture parfaite de l'interrupteur) donne lieu à un courant de charge infini.

Capacité et inductance

Cependant, le courant tiré par une paire de fils parallèles ne sera pas infini, car il existe une série d'impédance le long des fils due à l'inductance. (Figure ci-dessous) N'oubliez pas que le courant passe par tout conducteur développe un champ magnétique de grandeur proportionnelle. L'énergie est stockée dans ce champ magnétique (Figure ci-dessous) et ce stockage d'énergie se traduit par une opposition au changement de courant. Chaque fil développe un champ magnétique car il transporte un courant de charge pour la capacité entre les fils et, ce faisant, fait chuter la tension selon l'équation d'inductance e =L(di/dt). Cette chute de tension limite le taux de variation de tension à travers la capacité distribuée, empêchant le courant d'atteindre une amplitude infinie :

Circuit équivalent montrant la capacité parasite et l'inductance.

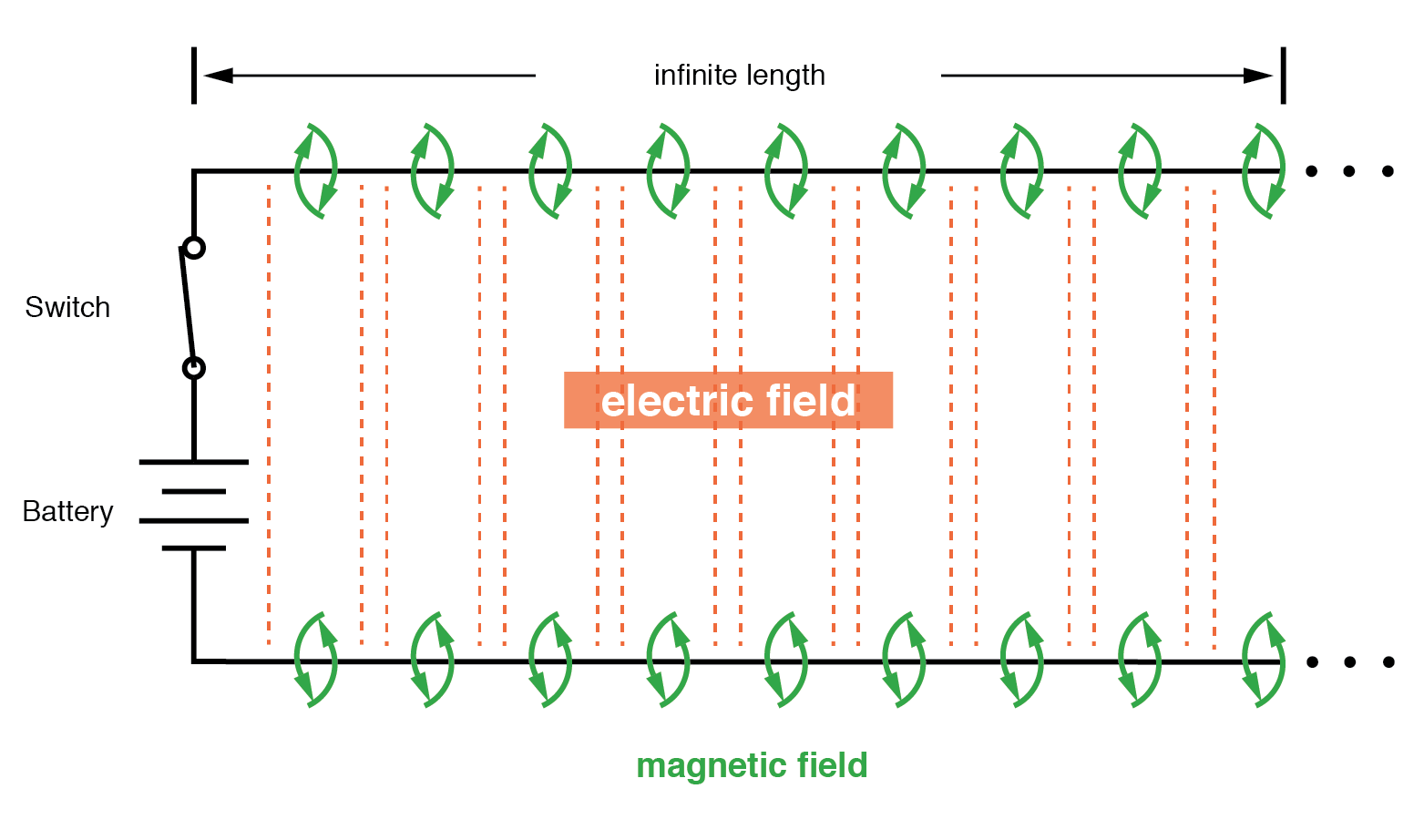
Capacité de charge de tension, inductance de charge de courant.

Étant donné que les porteurs de charge électrique dans les deux fils transfèrent le mouvement l'un vers l'autre presque à la vitesse de la lumière, le « front d'onde » du changement de tension et de courant se propagera le long des fils à la même vitesse, entraînant la distribution capacité et inductance se chargeant progressivement à pleine tension et courant, respectivement, comme ceci :

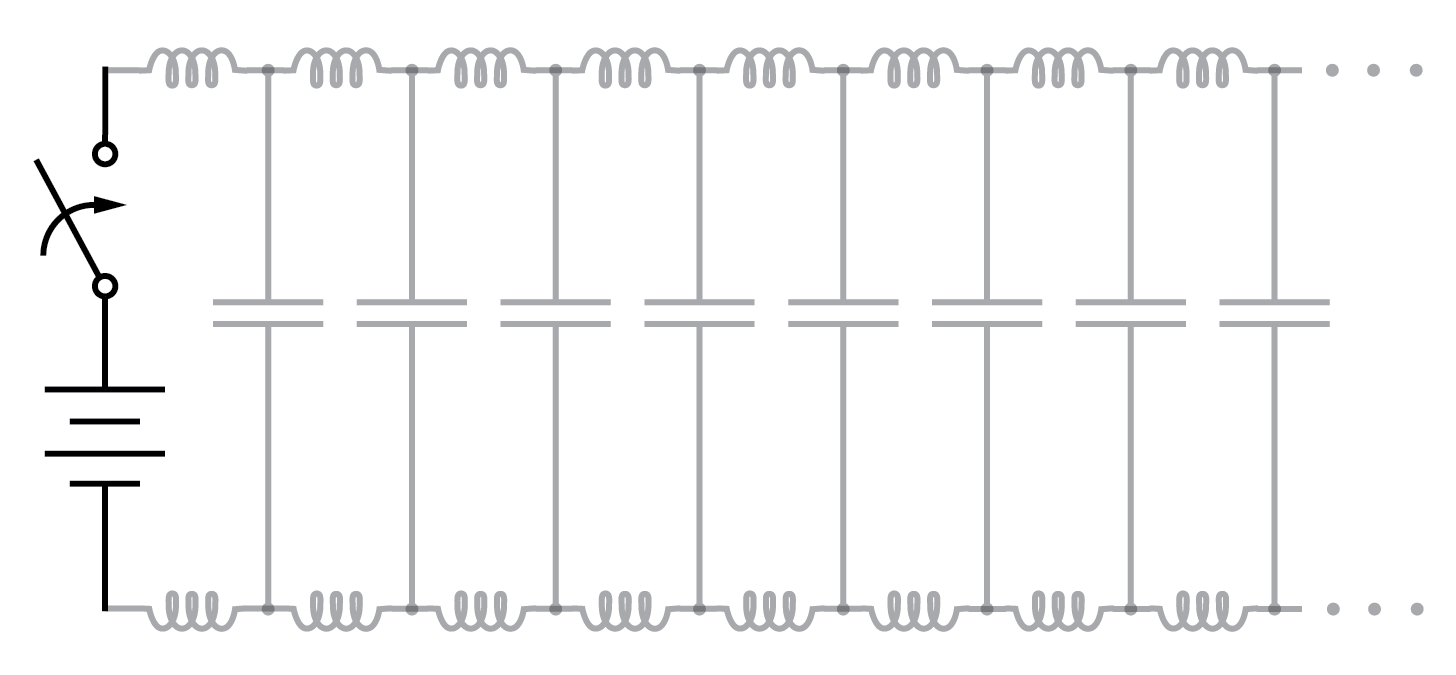
Ligne de transmission non chargée.

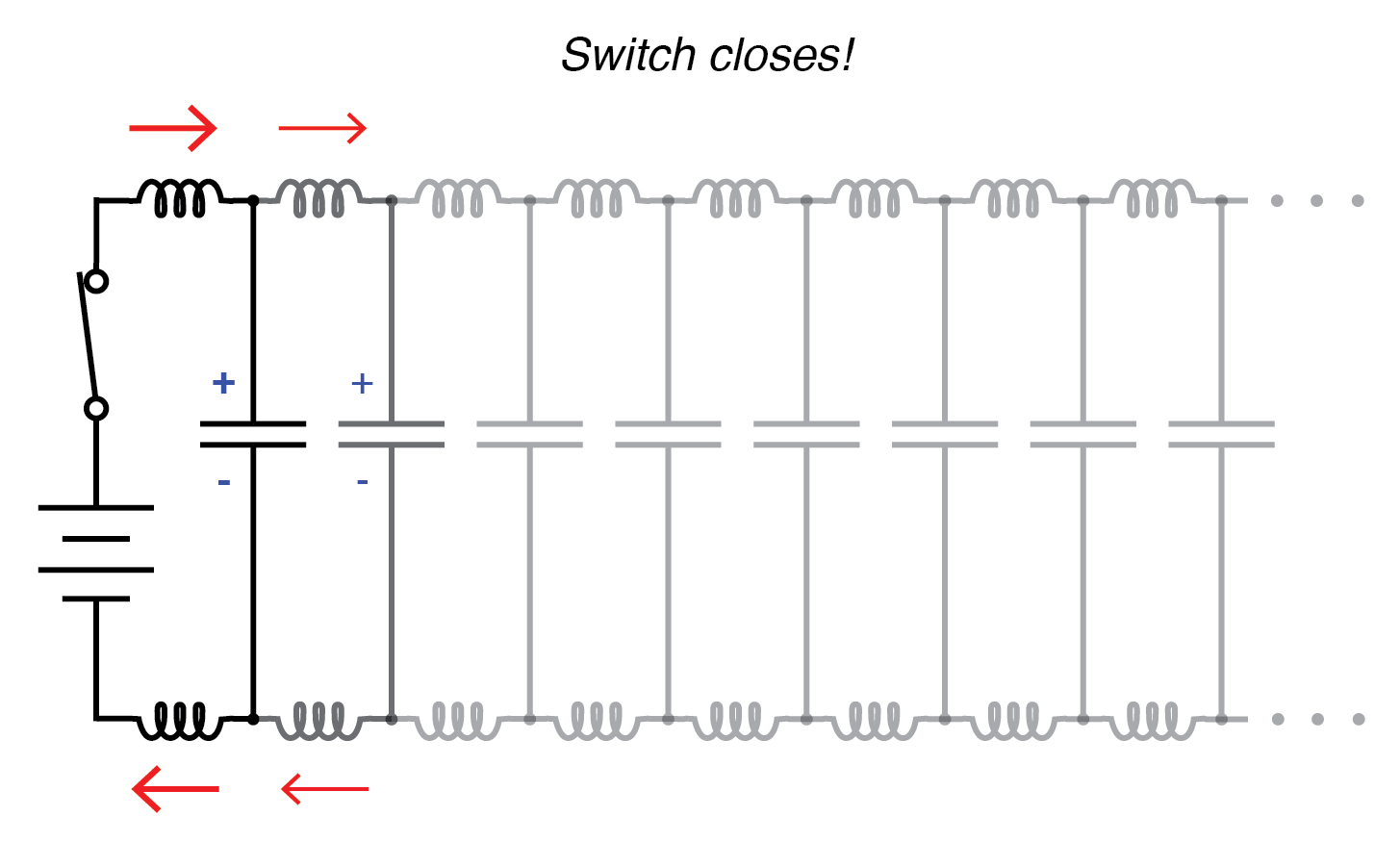
Commencer la propagation des ondes.

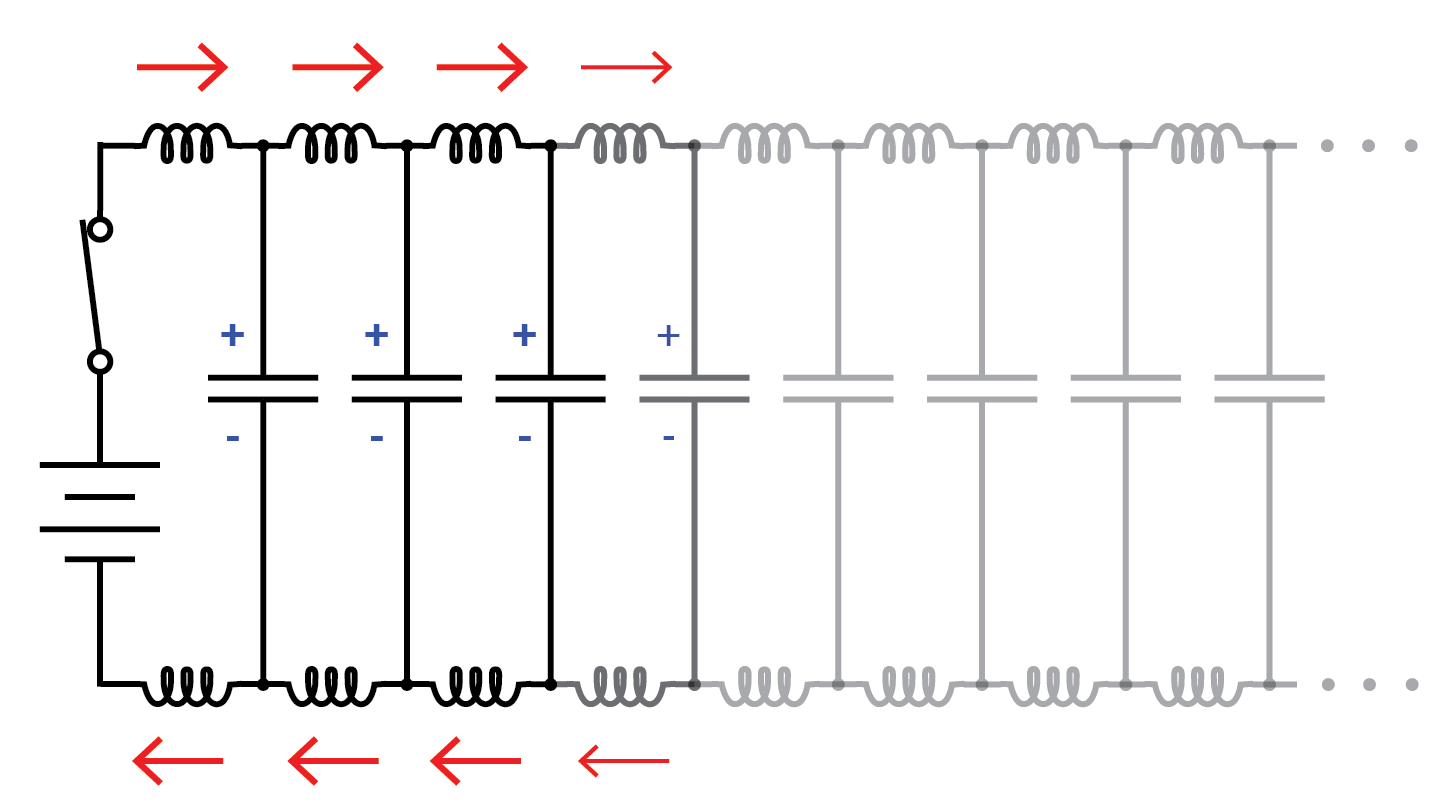
Continuer la propagation des ondes.

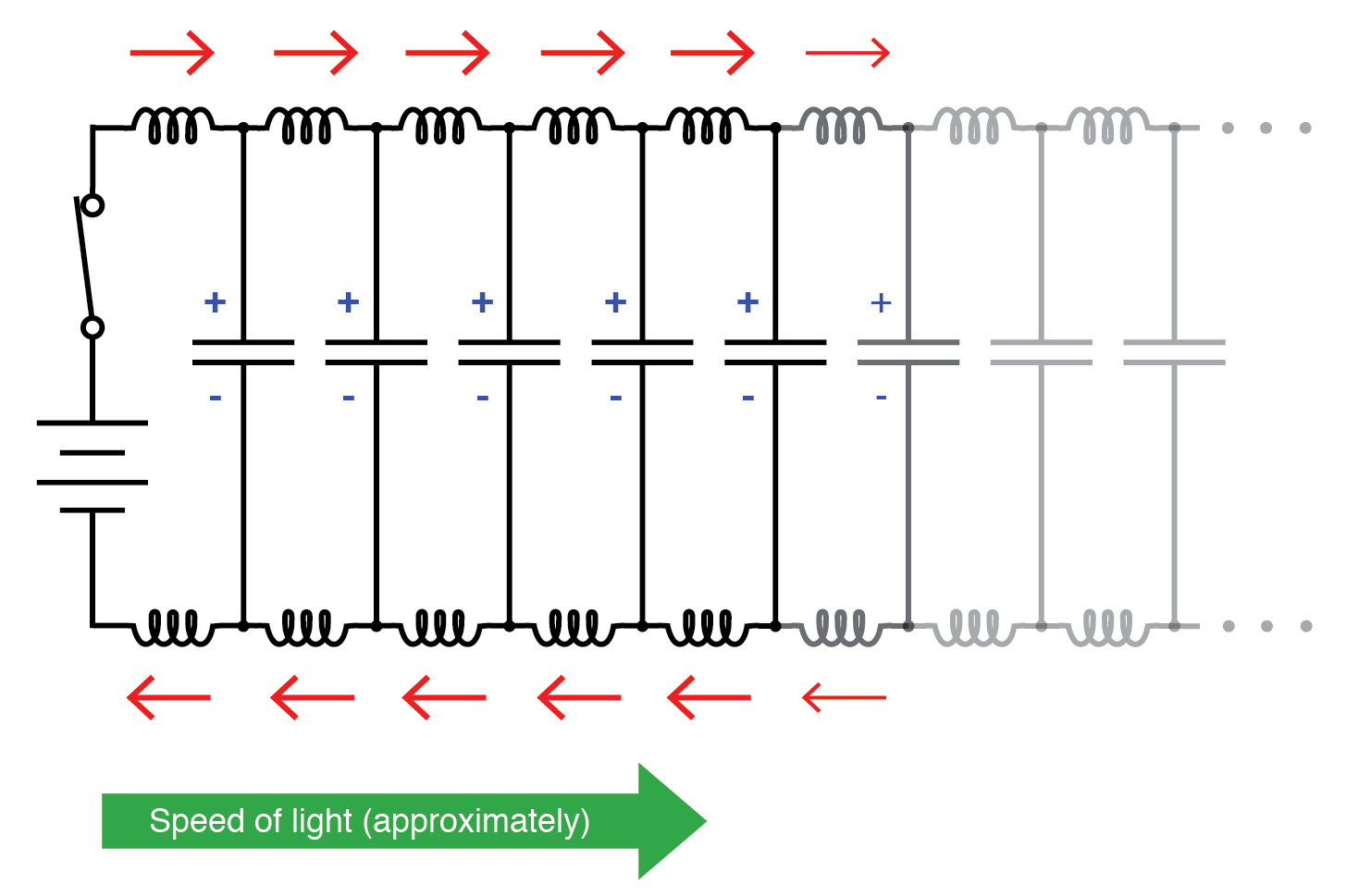
Propagez à la vitesse de la lumière.

La ligne de transmission

Le résultat final de ces interactions est un courant constant d'amplitude limitée à travers la source de la batterie. Étant donné que les fils sont infiniment longs, leur capacité distribuée ne se chargera jamais complètement à la tension source et leur inductance distribuée ne permettra jamais un courant de charge illimité. En d'autres termes, cette paire de fils tirera du courant de la source tant que l'interrupteur est fermé, se comportant comme une charge constante. Les fils ne sont plus simplement des conducteurs de courant électrique et des porteurs de tension, mais constituent désormais un composant de circuit en eux-mêmes, avec des caractéristiques uniques. Les deux fils ne sont plus simplement une paire de conducteurs , mais plutôt une ligne de transmission .

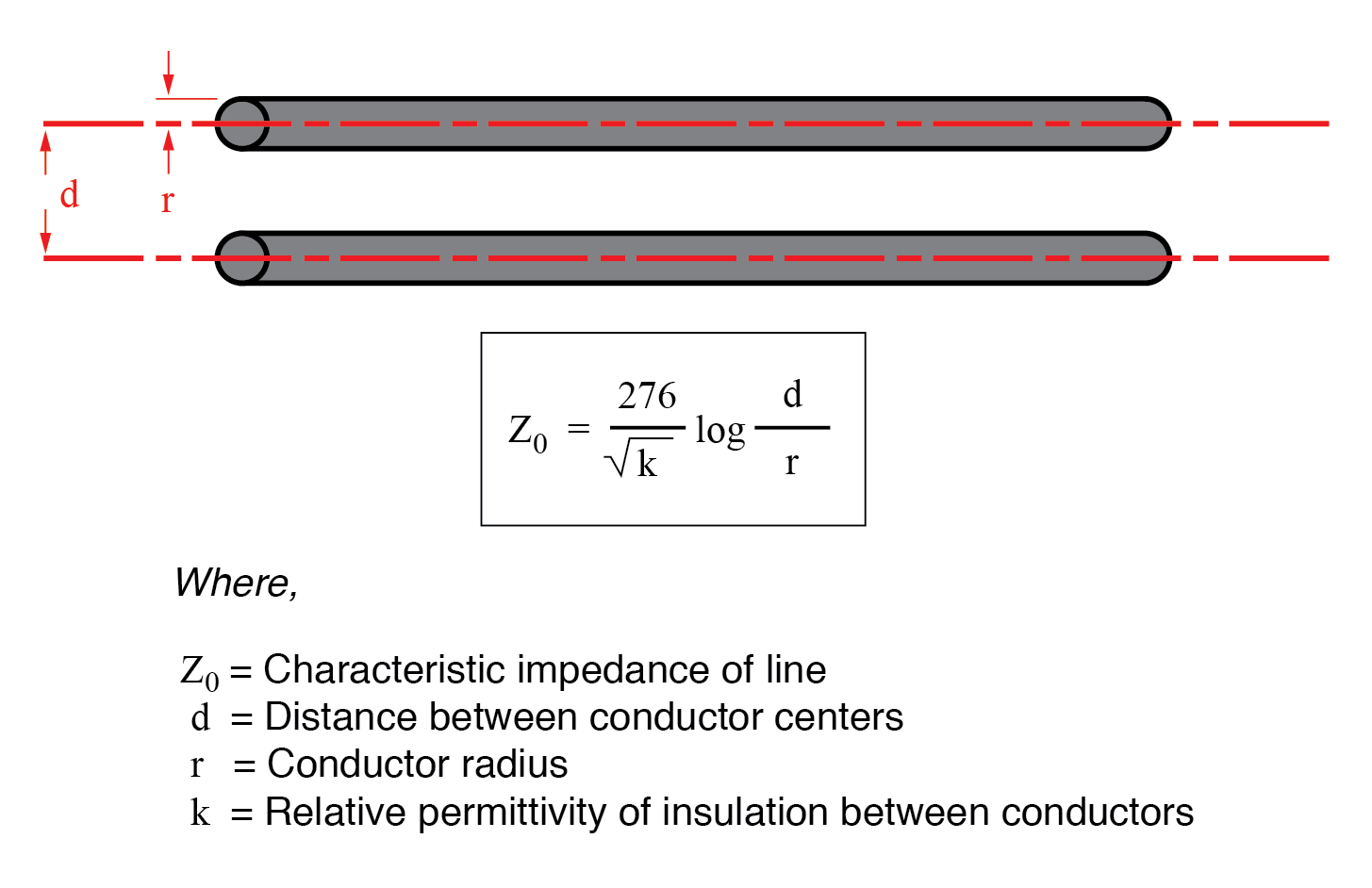
En tant que charge constante, la réponse de la ligne de transmission à la tension appliquée est résistive plutôt que réactive, bien qu'elle soit constituée uniquement d'inductance et de capacité (en supposant des fils supraconducteurs à résistance nulle). Nous pouvons dire cela parce qu'il n'y a pas de différence du point de vue de la batterie entre une résistance dissipant éternellement l'énergie et une ligne de transmission infinie absorbant éternellement l'énergie. L'impédance (résistance) de cette ligne en ohms est appelée impédance caractéristique , et il est fixé par la géométrie des deux conducteurs. Pour une ligne à fils parallèles avec isolation à l'air, l'impédance caractéristique peut être calculée comme telle :

Si la ligne de transmission est de construction coaxiale, l'impédance caractéristique suit une équation différente :

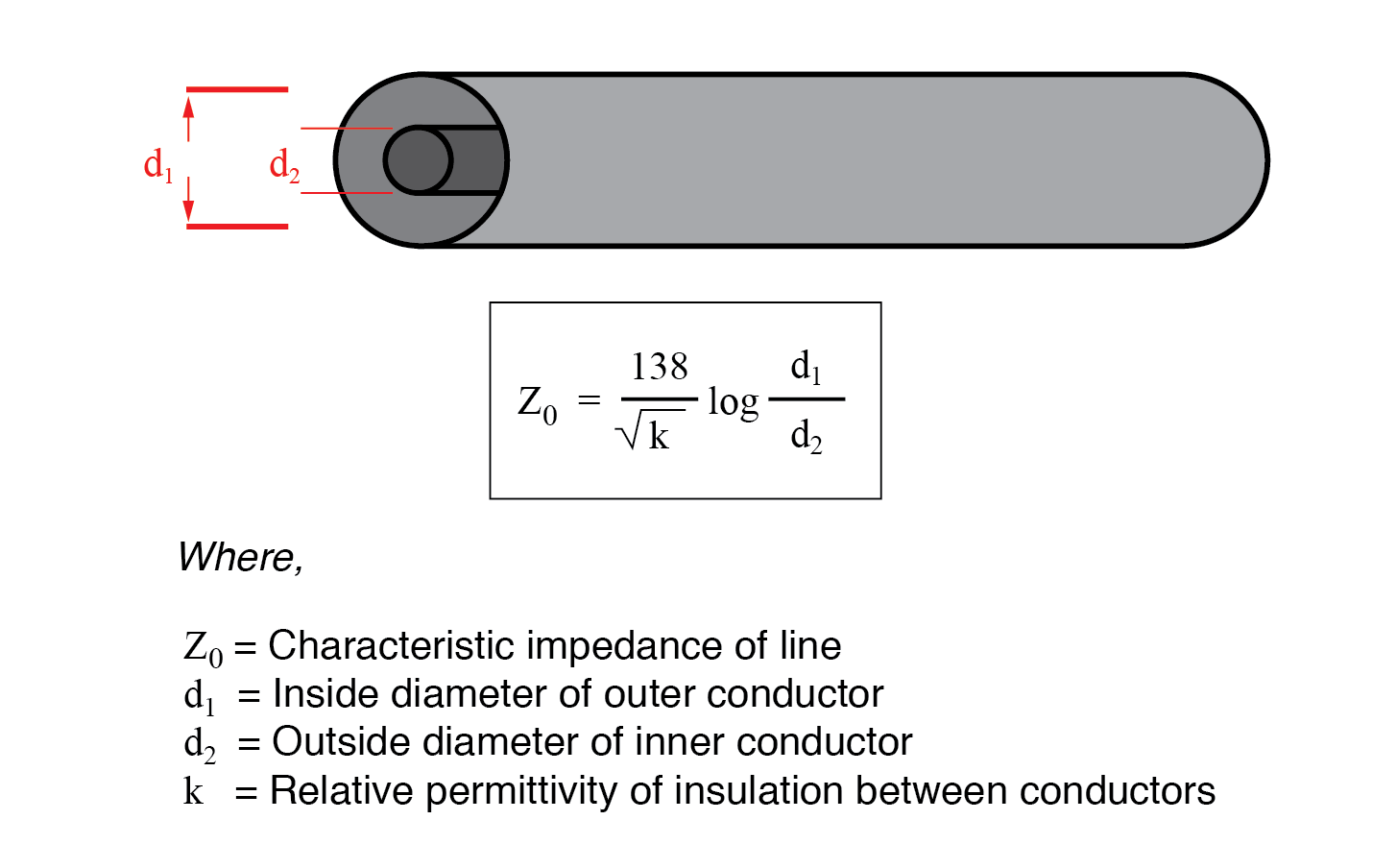
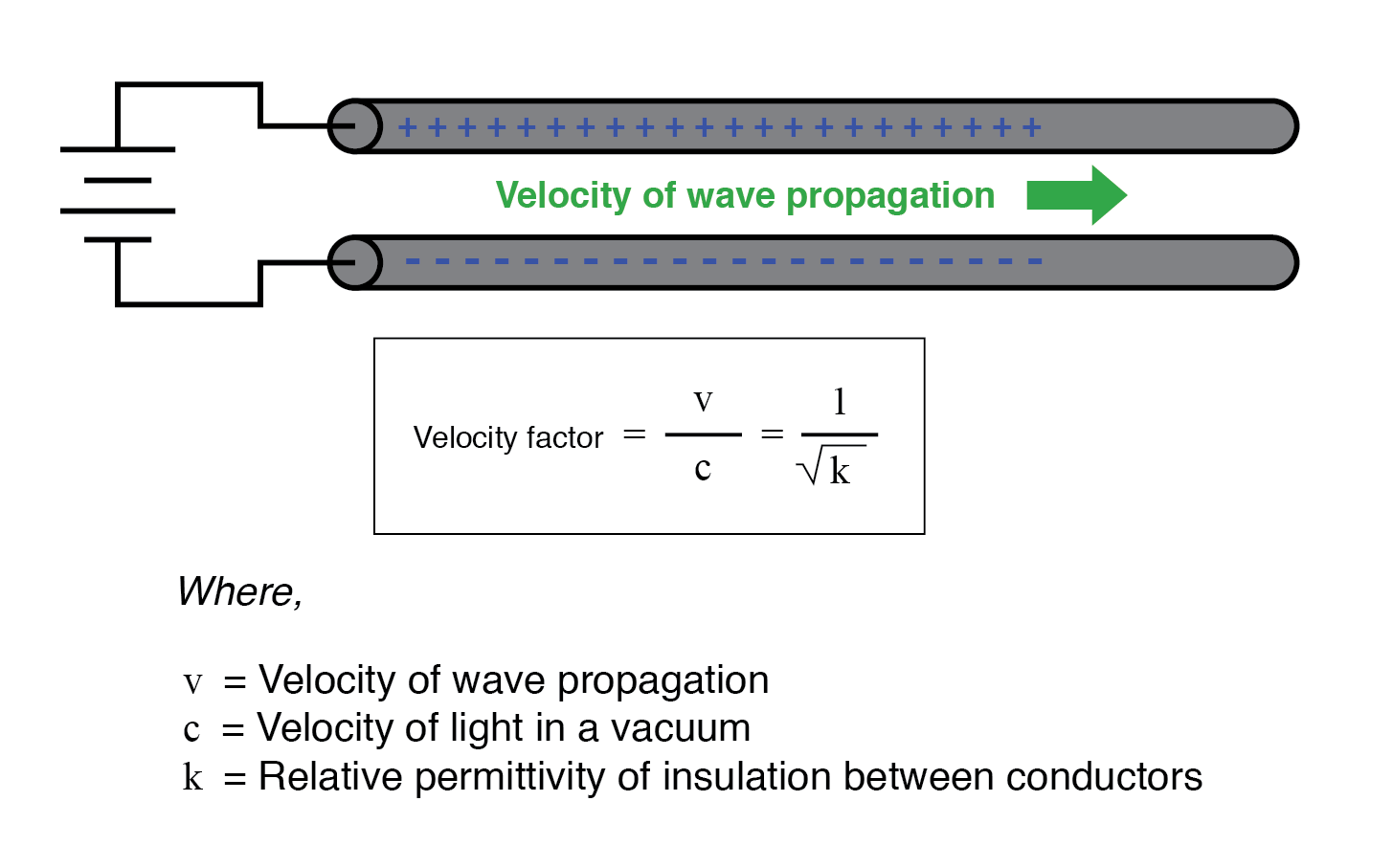
Dans les deux équations, des unités de mesure identiques doivent être utilisées dans les deux termes de la fraction. Si le matériau isolant n'est pas de l'air (ou un vide), à ​​la fois l'impédance caractéristique et la vitesse de propagation seront affectées. Le rapport entre la vitesse de propagation réelle d'une ligne de transmission et la vitesse de la lumière dans le vide est appelé le facteur de vitesse de cette ligne.

Le facteur de vitesse est purement un facteur de permittivité relative du matériau isolant (autrement appelé sa constante diélectrique ), défini comme le rapport de la permittivité du champ électrique d'un matériau à celle du vide pur. Le facteur de vitesse de tout type de câble—coaxial ou autre—peut être calculé tout simplement par la formule suivante :

L'impédance naturelle

L'impédance caractéristique est également appelée impédance naturelle , et il fait référence à la résistance équivalente d'une ligne de transmission si elle était infiniment longue, en raison de la capacité et de l'inductance distribuées lorsque les « ondes » de tension et de courant se propagent le long de sa longueur à une vitesse de propagation égale à une fraction importante de la vitesse de la lumière.

On peut voir dans l'une ou l'autre des deux premières équations que l'impédance caractéristique d'une ligne de transmission (Z₀ ) augmente à mesure que l'espacement des conducteurs augmente. Si les conducteurs sont éloignés les uns des autres, la capacité distribuée diminuera (espacement plus important entre les «plaques» de condensateur) et l'inductance distribuée augmentera (moins d'annulation des deux champs magnétiques opposés). Moins de capacité parallèle et plus d'inductance en série se traduisent par un courant plus petit tiré par la ligne pour une quantité donnée de tension appliquée, ce qui, par définition, est une plus grande impédance. A l'inverse, le rapprochement des deux conducteurs augmente la capacité parallèle et diminue l'inductance série. Les deux changements entraînent un courant plus important pour une tension appliquée donnée, ce qui équivaut à une impédance moindre.

À moins d'effets dissipatifs tels que les « fuites » diélectriques et la résistance des conducteurs, l'impédance caractéristique d'une ligne de transmission est égale à la racine carrée du rapport de l'inductance de la ligne par unité de longueur divisée par la capacité de la ligne par unité de longueur :

AVIS :

• Une ligne de transmission est une paire de conducteurs parallèles présentant certaines caractéristiques dues à une capacité et une inductance réparties sur sa longueur.
• Lorsqu'une tension est soudainement appliquée à une extrémité d'une ligne de transmission, une "onde" de tension et une "onde" de courant se propagent le long de la ligne à une vitesse proche de la lumière.
• Si une tension continue est appliquée à une extrémité d'une ligne de transmission infiniment longue, la ligne tirera du courant de la source continue comme s'il s'agissait d'une résistance constante.
• L'impédance caractéristique (Z₀ ) d'une ligne de transmission est la résistance qu'elle présenterait si sa longueur était infinie. Ceci est tout à fait différent de la résistance de fuite du diélectrique séparant les deux conducteurs et de la résistance métallique des fils eux-mêmes. L'impédance caractéristique est purement fonction de la capacité et de l'inductance réparties le long de la ligne et existerait même si le diélectrique était parfait (résistance parallèle infinie) et les fils supraconducteurs (résistance série nulle).
• Facteur de vitesse est une valeur fractionnaire relative à la vitesse de propagation d'une ligne de transmission à la vitesse de la lumière dans le vide. Les valeurs sont comprises entre 0,66 et 0,80 pour les lignes à deux fils et les câbles coaxiaux typiques. Pour tout type de câble, il est égal à l'inverse (1/x) de la racine carrée de la permittivité relative de l'isolation du câble.

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail de l'impédance caractéristique