Calculs de tension et de courant

Il existe un moyen sûr de calculer l'une des valeurs d'un circuit CC réactif au fil du temps.

Calcul des valeurs dans un circuit CC réactif

La première étape consiste à identifier les valeurs initiales et finales de la quantité dont le condensateur ou l'inducteur s'oppose au changement ; c'est-à-dire quelle que soit la quantité que le composant réactif essaie de maintenir constante. Pour les condensateurs, cette quantité est la tension; pour les inductances, cette quantité est courante . Lorsque le commutateur d'un circuit est fermé (ou ouvert), le composant réactif tentera de maintenir cette quantité au même niveau qu'avant la transition du commutateur, de sorte que cette valeur doit être utilisée pour la valeur « de départ ».

La valeur finale de cette quantité est quelle que soit cette quantité après un laps de temps infini. Cela peut être déterminé en analysant un circuit capacitif comme si le condensateur était un circuit ouvert et un circuit inductif comme si l'inducteur était un court-circuit, car c'est ainsi que ces composants se comportent lorsqu'ils ont atteint la « pleine charge ». après un temps infini.

L'étape suivante consiste à calculer la constante de temps du circuit :le temps qu'il faut pour que les valeurs de tension ou de courant changent d'environ 63 % de leurs valeurs de départ à leurs valeurs finales dans une situation transitoire.

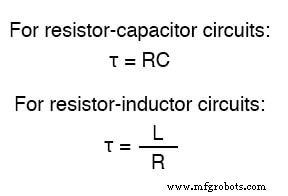
Dans un circuit RC en série, la constante de temps est égale à la résistance totale en ohms multipliée par la capacité totale en farads. Pour un circuit L/R en série, c'est l'inductance totale en henrys divisée par la résistance totale en ohms. Dans les deux cas, la constante de temps est exprimée en unités de secondes et symbolisé par la lettre grecque « tau » (τ) :

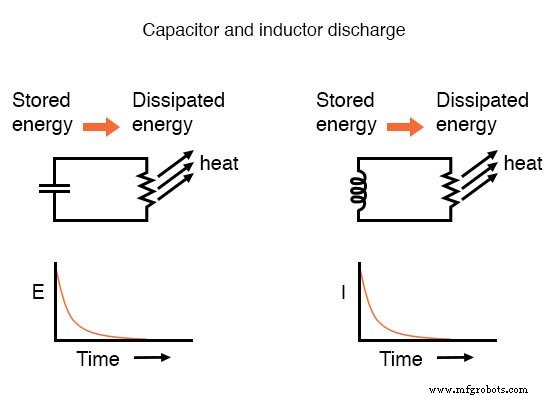
La montée et la chute des valeurs de circuit telles que la tension et le courant en réponse à un transitoire sont, comme cela a été mentionné précédemment, asymptotique . Cela étant, les valeurs commencent à changer rapidement peu de temps après le transitoire et s'installent avec le temps. Si elle est tracée sur un graphique, l'approche des valeurs finales de tension et de courant forme des courbes exponentielles.

Comme indiqué précédemment, une constante de temps est le temps qu'il faut à l'une de ces valeurs pour changer d'environ 63 % de leurs valeurs de départ à leurs valeurs finales (ultimes). Pour chaque constante de temps, ces valeurs se rapprochent (environ) de 63 % de leur objectif final. La formule mathématique pour déterminer le pourcentage précis est assez simple :

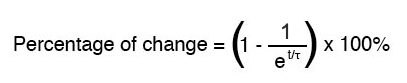
La lettre e représente la constante d'Euler, qui est d'environ 2,7182818. Il est dérivé de techniques de calcul, après analyse mathématique de l'approche asymptotique des valeurs du circuit. Après une valeur de constante de temps, le pourcentage de changement de la valeur de départ à la valeur finale est :

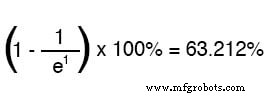
Après la valeur de deux constantes de temps, le pourcentage de changement de la valeur de départ à la valeur finale est :

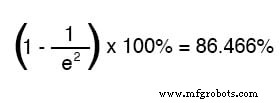
Après dix constantes de temps, le pourcentage est :

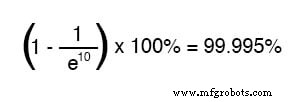
Plus le temps qui s'écoule depuis l'application transitoire de la tension de la batterie est long, plus la valeur du dénominateur dans la fraction est grande, ce qui donne une valeur plus petite pour la fraction entière, ce qui donne un total général (1 moins la fraction) approchant 1, ou 100 %.

Formule de constante de temps universel

Nous pouvons faire une formule plus universelle de celle-ci pour la détermination des valeurs de tension et de courant dans les circuits transitoires, en multipliant cette quantité par la différence entre les valeurs finales et de démarrage du circuit :

Analysons l'élévation de tension sur le circuit résistance-condensateur série présenté au début du chapitre.

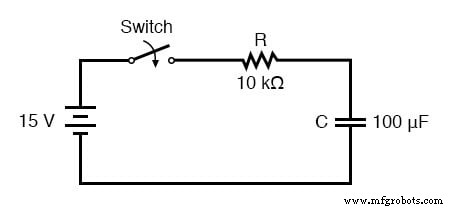
Notez que nous choisissons d'analyser la tension car c'est la quantité que les condensateurs ont tendance à maintenir constante. Bien que la formule fonctionne assez bien pour le courant, les valeurs initiales et finales du courant sont en fait dérivées de la tension du condensateur, de sorte que le calcul de la tension est une méthode plus directe. La résistance est de 10 kΩ et la capacité de 100 µF (microfarads). Puisque la constante de temps (τ) pour un circuit RC est le produit de la résistance et de la capacité, nous obtenons une valeur de 1 seconde :

Si le condensateur démarre dans un état totalement déchargé (0 volt), alors nous pouvons utiliser cette valeur de tension pour une valeur "de démarrage". La valeur finale, bien sûr, sera la tension de la batterie (15 volts). Notre formule universelle pour la tension du condensateur dans ce circuit ressemble à ceci :

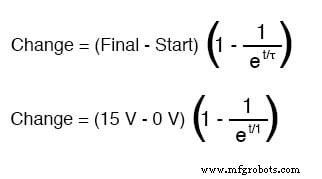
Ainsi, après 7,25 secondes d'application d'une tension à travers l'interrupteur fermé, notre tension de condensateur aura augmenté de :

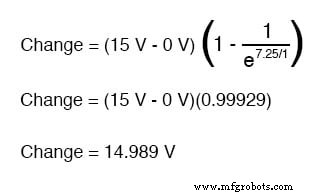
Puisque nous avons commencé à une tension de condensateur de 0 volt, cette augmentation de 14,989 volts signifie que nous avons 14,989 volts après 7,25 secondes.

La même formule fonctionnera également pour déterminer le courant dans ce circuit. Puisque nous savons qu'un condensateur déchargé agit initialement comme un court-circuit, le courant de démarrage sera le maximum possible :15 volts (de la batterie) divisés par 10 kΩ (la seule opposition au courant dans le circuit au début) :

Nous savons également que le courant final sera nul, puisque le condensateur finira par se comporter comme un circuit ouvert, ce qui signifie qu'à terme, aucun électron ne circulera dans le circuit. Maintenant que nous connaissons à la fois les valeurs de courant de démarrage et de fin, nous pouvons utiliser notre formule universelle pour déterminer le courant après 7,25 secondes de fermeture de l'interrupteur dans le même circuit RC :

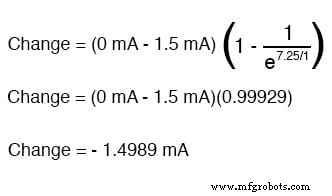
Notez que le chiffre obtenu pour le changement est négatif, pas positif ! Cela nous indique que le courant a diminué plutôt que d'augmenter avec le temps. Puisque nous avons commencé à un courant de 1,5 mA, cette diminution (-1,4989 mA) signifie que nous avons 0,001065 mA (1,065 µA) après 7,25 secondes.

Nous aurions également pu déterminer le courant du circuit au temps =7,25 secondes en soustrayant la tension du condensateur (14,989 volts) de la tension de la batterie (15 volts) pour obtenir la chute de tension aux bornes de la résistance de 10 kΩ, puis en calculant le courant à travers la résistance (et le tout le circuit série) avec la loi d'Ohm (I=E/R). Dans tous les cas, nous devrions obtenir la même réponse :

Utilisation de la formule de la constante de temps universelle pour l'analyse des circuits inductifs

La formule de constante de temps universelle fonctionne également bien pour analyser les circuits inductifs. Appliquons-le à notre exemple de circuit L/R au début du chapitre :

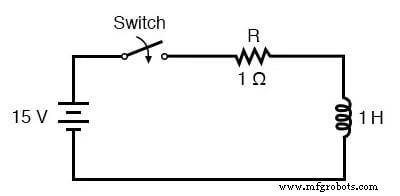
Avec une inductance de 1 henry et une résistance série de 1 Ω, notre constante de temps est égale à 1 seconde :

Parce qu'il s'agit d'un circuit inductif et que nous savons que les inductances s'opposent au changement de courant, nous allons configurer notre formule de constante de temps pour les valeurs de démarrage et finales du courant. Si nous commençons avec l'interrupteur en position ouverte, le courant sera égal à zéro, donc zéro est notre valeur de courant de départ.

Après que l'interrupteur est resté fermé pendant une longue période, le courant s'établira à sa valeur finale, égale à la tension de la source divisée par la résistance totale du circuit (I=E/R), ou 15 ampères dans le cas de ce circuit .

Si nous voulions déterminer la valeur du courant à 3,5 secondes, nous appliquerions la formule de la constante de temps universelle comme telle :

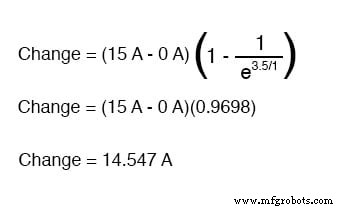
Étant donné que notre courant de démarrage était nul, cela nous laisse à un courant de circuit de 14,547 ampères à 3,5 secondes.

La détermination de la tension dans un circuit inductif est mieux accomplie en commençant par déterminer le courant du circuit, puis en calculant les chutes de tension à travers les résistances pour trouver ce qui reste à chuter à travers l'inducteur. Avec une seule résistance dans notre exemple de circuit (ayant une valeur de 1 Ω), c'est assez simple :

Soustrait de notre tension de batterie de 15 volts, cela laisse 0,453 volts à travers l'inducteur à temps =3,5 secondes.

AVIS :

• Formule de constante de temps universel :
• Pour analyser un circuit RC ou L/R, procédez comme suit :
• (1) :Déterminez la constante de temps du circuit (RC ou L/R).
• (2) :Identifiez la grandeur à calculer (quelle que soit la grandeur dont le changement est directement opposé par le composant réactif. Pour les condensateurs c'est la tension; pour les inductances c'est le courant).
• (3) :déterminez les valeurs de départ et de fin de cette quantité.
• (4) :branchez toutes ces valeurs (Final, Début, temps, constante de temps) dans la formule de constante de temps universelle et résolvez pour changer en quantité.
• (5) :Si la valeur de départ était zéro, alors la valeur réelle à l'instant spécifié est égale à la variation calculée donnée par la formule universelle. Sinon, ajoutez la modification à la valeur de départ pour savoir où vous en êtes.

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail sur les circuits à temps constant
• Feuille de travail sur les calculs des constantes de temps

Voir notre collection de Calculateurs de puissance dans notre Outils section .