Règle de diviseur de courant (CDR) - Exemples résolus pour les circuits AC et DC
Division de courant "CDR" pour les circuits résistifs, inductifs et capacitifs
Quoi est-ce que la règle de division actuelle (CDR) ?
Lorsqu'un certain nombre d'éléments sont connectés en parallèle, le courant se divise en un certain nombre de chemins parallèles. Et la tension est la même pour tous les éléments qui sont égaux à la tension source.
En d'autres termes, lorsque le courant passe par plus d'un chemin parallèle (la règle du diviseur de tension "VDR" ou division de tension est utilisée pour calculer la tension dans les circuits en série), la division actuelle dans chaque chemin. La valeur du courant passe par une branche particulière dépend de l'impédance de cette branche.
La règle de division actuelle ou la règle de division actuelle est la formule la plus importante largement utilisée pour résoudre les circuits. Nous pouvons trouver le courant qui traverse chaque branche si nous connaissons l'impédance de chaque branche et le courant total.
Le courant passe toujours par la moindre impédance. Ainsi, le courant a une relation inverse avec l'impédance. Selon la loi d'ohm, le courant qui entre dans le nœud sera divisé entre eux en proportion inverse de l'impédance.
Cela signifie que l'impédance de plus petite valeur a un courant plus grand car le courant a choisi le chemin le moins résistant. Et la résistance de plus grande valeur a le moins de courant.
Selon les éléments du circuit, la règle du diviseur de courant peut décrire des résistances, des inductances et des condensateurs.
Règle du diviseur de courant pour les circuits résistifs
Pour comprendre la règle du diviseur de courant résistif, prenons un circuit dans lequel les résistances sont connectées en parallèle. Le schéma du circuit est illustré dans la figure ci-dessous.
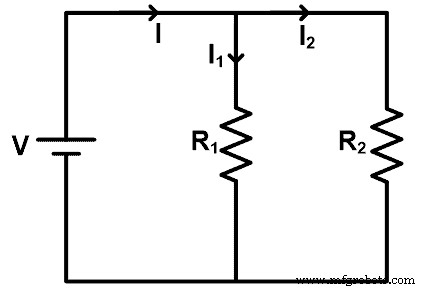
Dans cet exemple, une source d'alimentation CC à tous les résistors. La tension des résistances est la même que la tension de la source. Mais en raison de la connexion parallèle, le courant se divise en différents chemins. Le courant se divise à chaque nœud et la valeur du courant dépend de la résistance.
Nous pouvons directement trouver la valeur du courant traversant chaque résistance à l'aide de la règle du diviseur de courant.
Dans cet exemple, le courant principal fourni par la source est I. Et il se divise en deux résistances R1 et R2 . Le courant traverse la résistance R1 est I1 et le courant traverse la résistance R2 est I2 .
Comme les résistances sont connectées en parallèle. Ainsi, la résistance équivalente est Req .
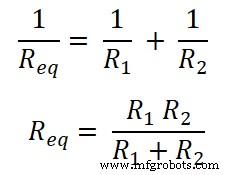
Maintenant, selon la loi d'Ohm ;
V =I Req
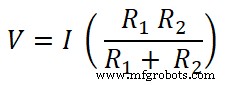
Les deux résistances sont connectées en parallèle avec une source CC. Par conséquent, la tension aux bornes de la résistance est la même que la tension de la source. Et le courant qui traverse la résistance R1 est I1 .
Donc, pour le résistant R1;
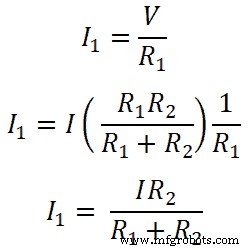
De même, pour le résistant R2;
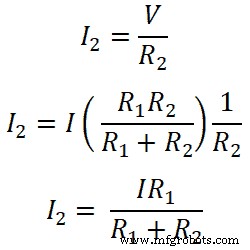
Ainsi, ces équations montrent une règle de diviseur de courant pour la résistance connectée en parallèle. À partir de ces équations, nous pouvons dire que le courant qui traverse la résistance est égal au rapport de multiplication du courant total et de la résistance opposée avec la résistance totale.
Messages associés :
- Théorème de Thévenin. Guide étape par étape avec exemple résolu
- Théorème de Norton. Guide étape par étape avec exemple résolu
Règle du diviseur de courant pour les circuits inductifs
Lorsque les inductances sont connectées en parallèle, nous pouvons appliquer la règle du diviseur de courant pour trouver le courant qui traverse chaque inductance. Pour comprendre la règle du diviseur de courant, prenons un circuit dans lequel les inductances sont connectées en parallèle comme le montre la figure ci-dessous.
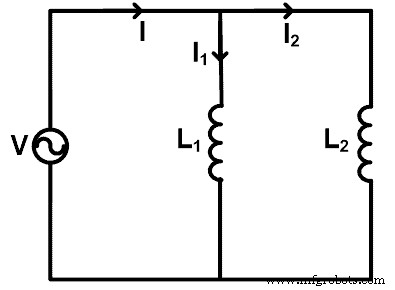
Ici, deux inducteurs (L1 et L2 ) sont connectés en parallèle avec une source de tension V. Le courant total traversant la source est de 1 ampère. Le courant passe par l'inductance L1 est I1 et le courant passe par l'inductance L2 est I2 .
Maintenant, nous devons trouver les équations pour le courant I1 et moi2 . Pour cela, on trouvera l'inductance équivalente Leq;
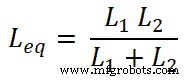
Nous savons que le courant total qui traverse le circuit est I et qu'il est égal à ;
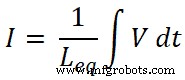
Donc,
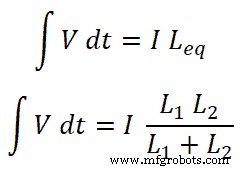
Maintenant, pour l'inductance L1 , le courant qui traverse cette inductance est I1;
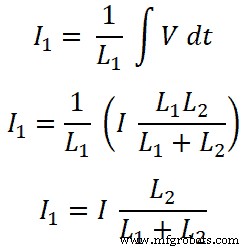
Pour l'inductance L2;
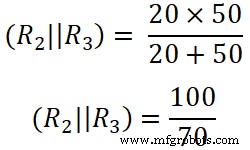
La règle de division actuelle pour l'inductance est la même que la règle de division actuelle pour les résistances.
Règle de diviseur de courant pour les circuits capacitifs
Lorsque les condensateurs sont connectés en parallèle, nous pouvons trouver le courant qui traverse chaque condensateur en utilisant la règle du diviseur de courant. Pour comprendre la règle du diviseur de courant pour le condensateur, prenons un exemple dans lequel les condensateurs sont connectés en parallèle, comme indiqué dans la figure ci-dessous.
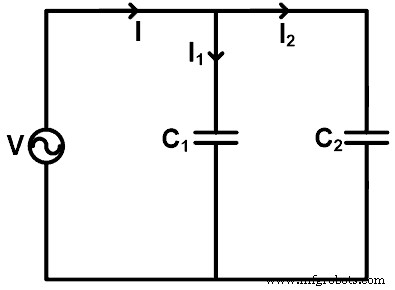
Ici, deux condensateurs (C1 et C2 ) sont connectés en parallèle avec une source de tension V. Le courant traverse le condensateur C1 est I1, et le courant traverse le condensateur C2 est I2 . Le courant total fourni par la source est I.
Maintenant, nous devons trouver les équations pour le courant I1 et moi2 . Pour cela, on trouvera la capacité équivalente Ceq;
Ceq =C 1 + C 2
Nous connaissons l'équation du courant qui traverse le condensateur. Et l'équation du courant total fourni par la source est :
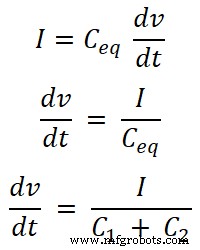
Pour le condensateur C1 , le courant qui traverse ce condensateur est I1;
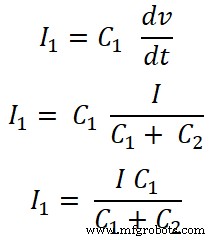
Pour le condensateur C2;
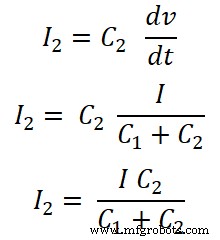
La règle de division actuelle pour le condensateur est légèrement différente de la règle de division actuelle pour l'inductance et la résistance.
Dans la règle du diviseur de courant du condensateur, le courant qui traverse un condensateur est un rapport du courant total multiplié par ce condensateur à la capacité totale.
Exemples résolus pour les circuits AC et DC utilisant CDR
Règle de plongeur de courant pour circuit CC
Exemple : 1
Trouvez le courant qui traverse chaque résistance par la règle de diviseur de courant pour le réseau donné.
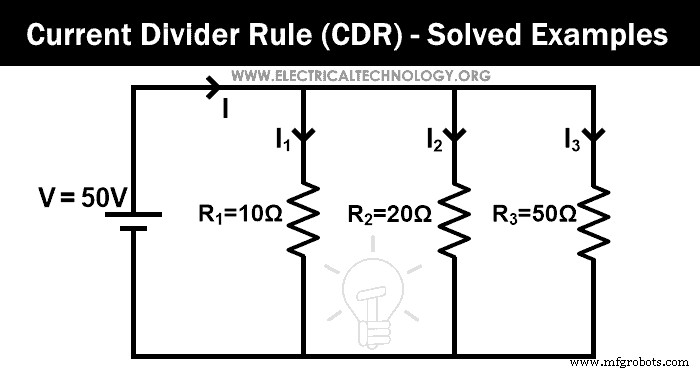
Dans cet exemple, trois résistances sont connectées en parallèle. Tout d'abord, nous trouvons la résistance équivalente.
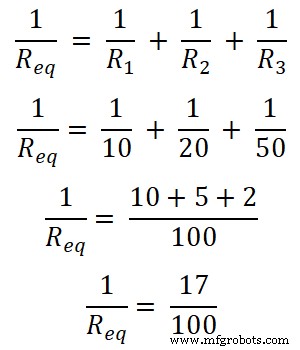
Req = 100/17
Req = 5.882 Ω
Le courant total fourni par la source est I. Donc, selon la loi d'ohm ;
V =I Req
50 V =je (5.882Ω)
Je = 50V / 5.882Ω
Je = 8.5A
Maintenant, nous appliquons la règle du diviseur de courant à la première résistance (10 Ω), et le courant qui traverse cette résistance est I1;
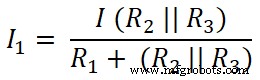
Ici R2 et R3 sont connectés en parallèle. Donc, nous devons trouver la résistance équivalente entre R2 et R3 .
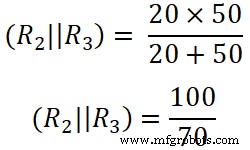
(R 2 || R 3 ) =14,285 Ω
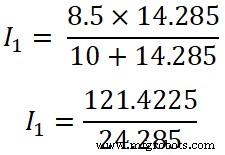
Je 1 =4,9999 ≈ 5 A
De même, nous appliquons la règle du diviseur de courant à la deuxième résistance (20 Ω), et le courant qui traverse cette résistance est I2;
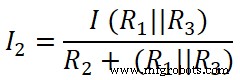
Ici,
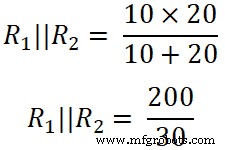
(R 1 || R 3 ) =8,33 Ω
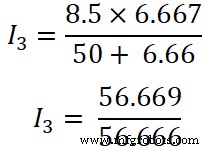
Je 2 =2,499 ≈ 2,5 A
Maintenant, nous appliquons la règle du diviseur de courant à la troisième résistance (50 Ω), et le courant qui traverse cette résistance est I3 .
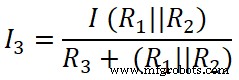
Ici,
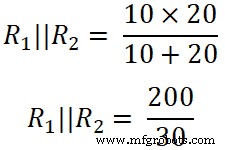
(R 1 || R 2 ) =6,66 Ω
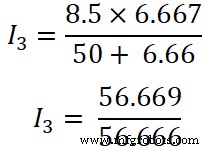
Je 3 =1,00 A
Ainsi, la somme des trois courants sera ;
Je 1 + je 2 + je 3 =5 + 2,5 + 1 =8,5 A
Et ce courant est le même que le courant total fourni par la source.
Règle de plongeur actuelle pour le circuit AC
Exemple-2
Considérez un circuit CA ayant une résistance et un condensateur connectés en parallèle, comme indiqué dans la figure ci-dessous. Trouvez le courant qui traverse la résistance et le condensateur en utilisant la règle du diviseur de courant. Envisagez une fréquence de 60 Hz.
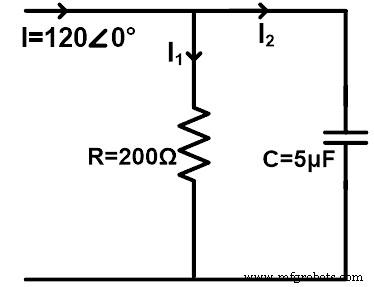
ZR =200Ω =200∠0°Ω
ZC =1/(2 πf C) =1/(2 π 60(5×10 6 ) )
ZC =10 6 / (600 π)
ZC =530,78 ∠-90° Ω
Maintenant, selon la règle du diviseur de courant, l'équation du courant qui traverse la résistance est ;
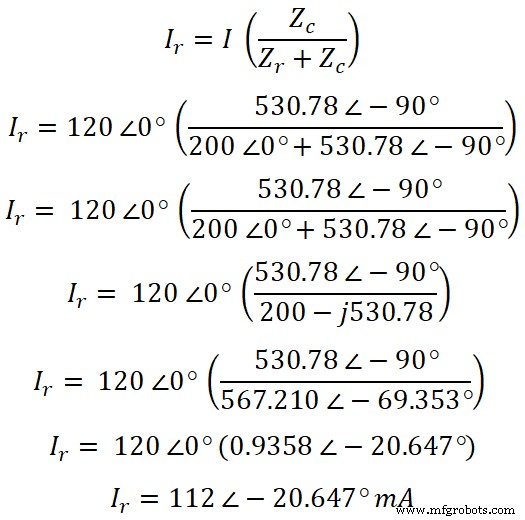
Maintenant, de la même manière, nous pouvons trouver le courant qui traverse le condensateur. Selon la règle du diviseur de courant, l'équation du courant traversant le condensateur est :
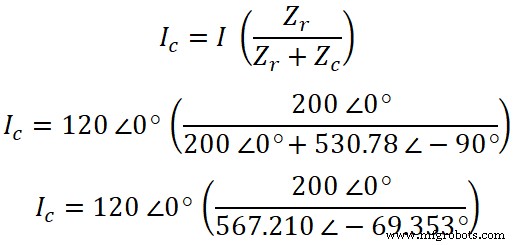
IC =120 ∠0° (0,3526 ∠ 69,353°)
IC =42,31 ∠ 69,353°
Si vous voulez prouver cette réponse, vous pouvez ajouter les deux courants. Et la valeur de ce courant est la même que le courant source.
Tutoriels d'analyse de circuit électrique associés :
- Théorème de compensation :preuve, explication et exemples résolus
- Théorème de substitution – Guide étape par étape avec exemple résolu
- Analyse de circuit SUPERNODE – Étape par étape avec exemple résolu
- Analyse de circuit SUPERMESH - étape par étape avec exemple résolu
- Loi du courant et de la tension de Kirchhoff (KCL et KVL) | Exemple résolu
- Calculateur de règles de Cramer – Système d'équations à 2 et 3 équations pour les circuits électriques
- Pont de Wheatstone – Circuit, fonctionnement, dérivation et applications
- Calculatrices d'ingénierie électrique et électronique
- Plus de 5 000 formules et équations d'ingénierie électrique et électronique
Technologie industrielle



