théorème de superposition

Le théorème de superposition est l'un de ces coups de génie qui prend un sujet complexe et le simplifie d'une manière parfaitement logique. Un théorème comme celui de Millman fonctionne certainement bien, mais ce n'est pas tout à fait évident pourquoi ça marche si bien. La superposition, en revanche, est évidente.

Analyse en série/parallèle

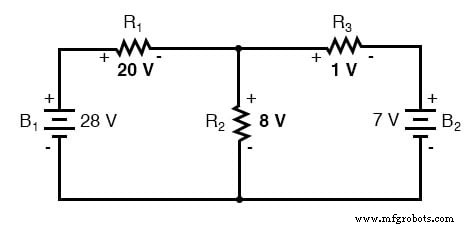
La stratégie utilisée dans le théorème de superposition consiste à éliminer toutes les sources d'alimentation d'un réseau à la fois, sauf une, en utilisant une analyse série/parallèle pour déterminer les chutes de tension (et/ou les courants) dans le réseau modifié pour chaque source d'alimentation séparément. Ensuite, une fois que les chutes de tension et/ou les courants ont été déterminés pour chaque source d'alimentation fonctionnant séparément, les valeurs sont toutes « superposées » les unes sur les autres (additionnées algébriquement) pour trouver les chutes de tension/courants réels avec toutes les sources actives. Regardons à nouveau notre exemple de circuit et appliquons-y le théorème de superposition :

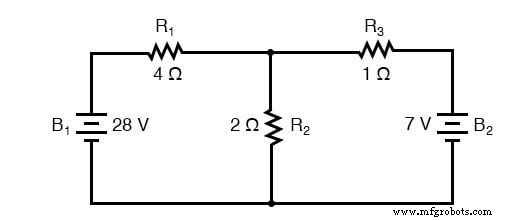
Puisque nous avons deux sources d'alimentation dans ce circuit, nous devrons calculer deux ensembles de valeurs pour les chutes de tension et/ou les courants, un pour le circuit avec uniquement la batterie de 28 volts. . .

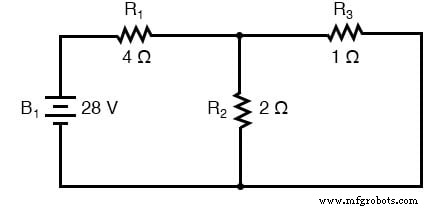
. . . et un pour le circuit avec uniquement la batterie 7 volts en vigueur :

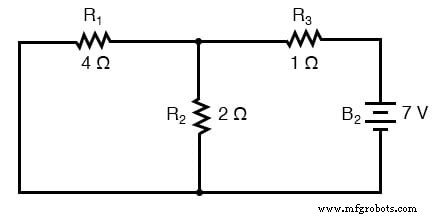
Lorsque vous redessinez le circuit pour une analyse série/parallèle avec une source, toutes les autres sources de tension sont remplacées par des fils (courts-circuits) et toutes les sources de courant avec des circuits ouverts (ruptures). Comme nous n'avons que des sources de tension (batteries) dans notre exemple de circuit, nous remplacerons chaque source inactive lors de l'analyse par un fil.

En analysant le circuit avec uniquement la batterie de 28 volts, nous obtenons les valeurs suivantes pour la tension et le courant :

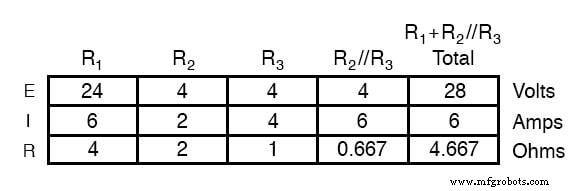
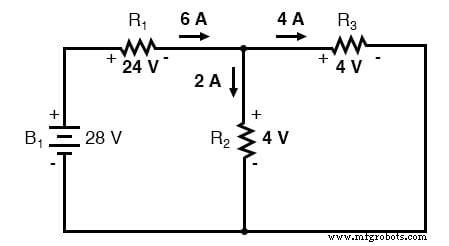
En analysant le circuit avec uniquement la batterie 7 volts, nous obtenons un autre ensemble de valeurs pour la tension et le courant :

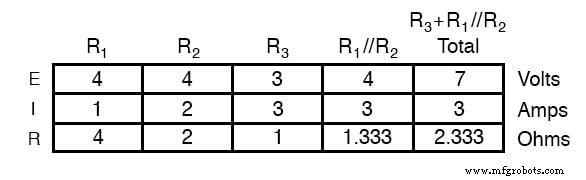
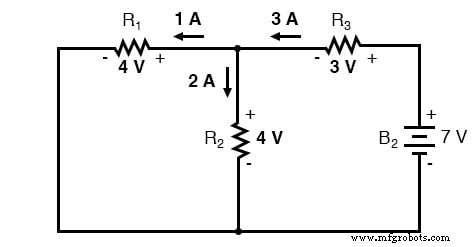
Par superposition

Lors de la superposition de ces valeurs de tension et de courant, nous devons faire très attention à considérer la polarité (de la chute de tension) et la direction (du courant), car les valeurs doivent être additionnées algébriquement .

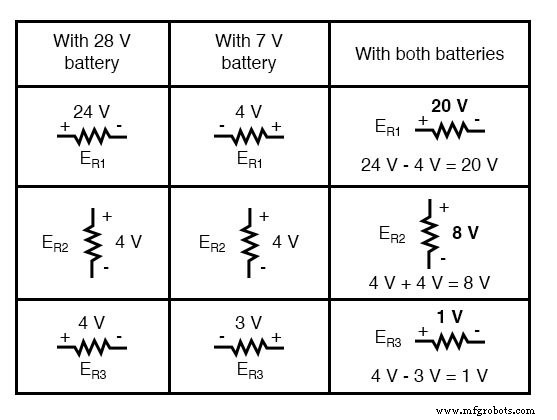
En appliquant ces chiffres de tension superposés au circuit, le résultat final ressemble à ceci :

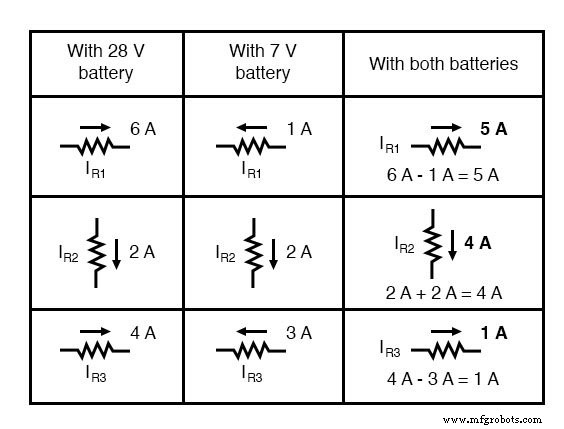
Les courants s'additionnent également algébriquement et peuvent être superposés comme cela se fait avec les chutes de tension des résistances ou simplement calculés à partir des chutes de tension finales et des résistances respectives (I=E/R). Dans tous les cas, les réponses seront les mêmes. Ici, je vais montrer la méthode de superposition appliquée au courant :

En appliquant à nouveau ces chiffres superposés à notre circuit :

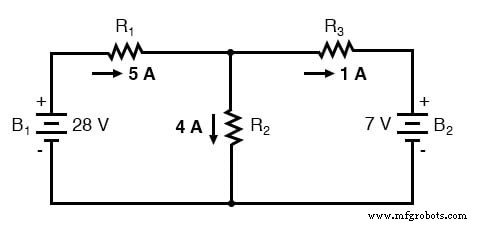
Prérequis pour le théorème de superposition

Assez simple et élégant, vous ne trouvez pas ? Il faut cependant noter que le théorème de superposition ne fonctionne que pour les circuits réductibles à des combinaisons série/parallèle pour chacune des sources d'alimentation à la fois (ce théorème est donc inutile pour analyser un circuit en pont déséquilibré), et il fonctionne là où les équations sous-jacentes sont linéaires (pas de puissances mathématiques ni de racines). La condition de linéarité signifie que le théorème de superposition n'est applicable que pour déterminer la tension et le courant, pas la puissance !!! Les dissipations de puissance, étant des fonctions non linéaires, ne s'additionnent pas algébriquement à un total précis lorsqu'une seule source est considérée à la fois. Le besoin de linéarité signifie également que ce théorème ne peut pas être appliqué dans des circuits où la résistance d'un composant change avec la tension ou le courant. Par conséquent, les réseaux contenant des composants tels que des lampes (à incandescence ou à décharge) ou des varistances n'ont pas pu être analysés.

Une autre condition préalable au théorème de superposition est que tous les composants doivent être «bilatéraux», ce qui signifie qu'ils se comportent de la même manière avec les électrons qui les traversent dans les deux sens. Les résistances n'ont pas de comportement spécifique à la polarité, et donc les circuits que nous avons étudiés jusqu'à présent répondent tous à ce critère.

Le théorème de superposition trouve une utilisation dans l'étude des circuits à courant alternatif (AC) et des circuits à semi-conducteurs (amplificateurs), où parfois AC est souvent mélangé (superposé) avec DC. Étant donné que les équations de tension alternative et de courant (loi d'Ohm) sont linéaires tout comme le courant continu, nous pouvons utiliser la superposition pour analyser le circuit avec uniquement la source d'alimentation CC, puis uniquement la source d'alimentation CA, en combinant les résultats pour dire ce qui se passera avec le courant alternatif et Sources CC en vigueur. Pour l'instant, cependant, la superposition suffira pour éviter d'avoir à faire des équations simultanées pour analyser un circuit.

AVIS :

• Le théorème de superposition indique qu'un circuit peut être analysé avec une seule source d'alimentation à la fois, les tensions et courants des composants correspondants étant ajoutés algébriquement pour savoir ce qu'ils feront avec toutes les sources d'alimentation en vigueur.
• Pour annuler toutes les sources d'alimentation sauf une pour l'analyse, remplacez toute source de tension (piles) par un fil ; remplacer toute source actuelle par un open (break).

FEUILLE DE TRAVAIL CONNEXE :

• Fiche de travail sur le théorème de superposition