Exemples de simplification de circuits

Commençons par un circuit de porte semi-conducteur nécessitant une simplification.

Les signaux d'entrée « A », « B » et « C » sont supposés être fournis par des commutateurs, des capteurs ou peut-être d'autres circuits de porte.

L'origine de ces signaux n'a pas d'importance dans la tâche de réduction de porte.

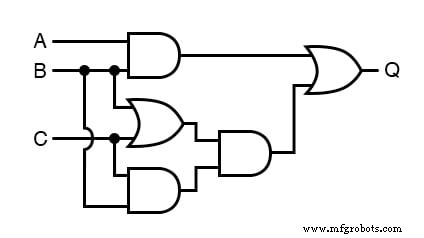
Comment écrire une expression booléenne pour simplifier les circuits

Notre première étape de simplification doit être d'écrire une expression booléenne pour ce circuit.

Cette tâche est facilement réalisée étape par étape si nous commençons par écrire des sous-expressions à la sortie de chaque porte, correspondant aux signaux d'entrée respectifs pour chaque porte.

N'oubliez pas que les portes OU sont équivalentes à l'addition booléenne, tandis que les portes ET sont équivalentes à la multiplication booléenne.

Par exemple, j'écrirai des sous-expressions aux sorties des trois premières portes :

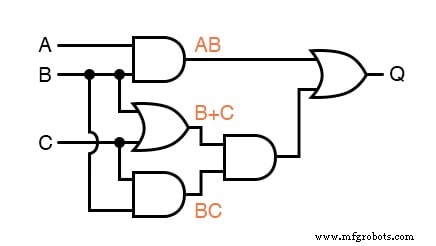
. . . puis une autre sous-expression pour la porte suivante :

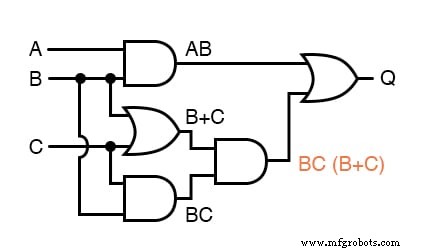
Enfin, la sortie ("Q") est considérée comme étant égale à l'expression AB + BC(B + C) :

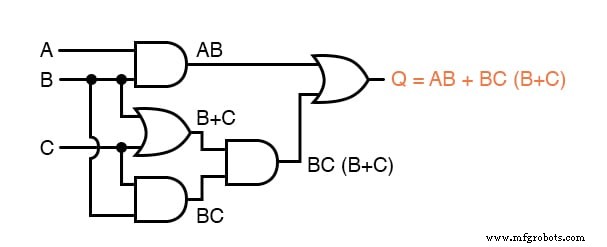
Maintenant que nous avons une expression booléenne avec laquelle travailler, nous devons appliquer les règles de l'algèbre booléenne pour réduire l'expression à sa forme la plus simple (la plus simple étant définie comme nécessitant le moins de portes à implémenter) :

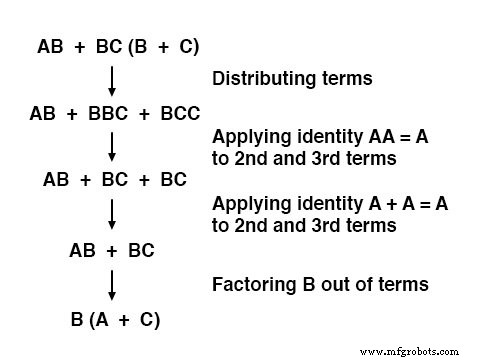
L'expression finale, B(A + C), est beaucoup plus simple que l'originale, mais remplit la même fonction.

Si vous souhaitez vérifier cela, vous pouvez générer une table de vérité pour les deux expressions et déterminer l'état de Q (la sortie des circuits) pour les huit combinaisons d'états logiques A, B et C, pour les deux circuits. Les deux tables de vérité doivent être identiques.

Génération de diagrammes schématiques à partir d'expressions booléennes

Maintenant, nous devons générer un diagramme schématique à partir de cette expression booléenne.

Pour ce faire, évaluez l'expression en suivant l'ordre mathématique approprié des opérations (multiplication avant addition, opérations entre parenthèses avant toute autre chose) et dessinez des portes pour chaque étape.

Rappelez-vous encore que les portes OU sont équivalentes à l'addition booléenne, tandis que les portes ET sont équivalentes à la multiplication booléenne.

Dans ce cas, nous commencerions par la sous-expression « A + C », qui est une porte OU :

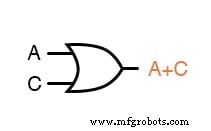
L'étape suivante de l'évaluation de l'expression « B(A + C) » consiste à multiplier (porte ET) le signal B par la sortie de la porte précédente (A + C) :

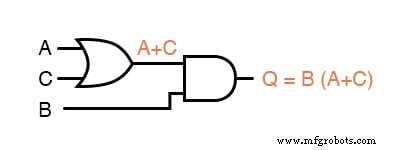
Évidemment, ce circuit est beaucoup plus simple que l'original, n'ayant que deux portes logiques au lieu de cinq.

Une telle réduction des composants se traduit par une vitesse de fonctionnement plus élevée (moins de temps de retard entre la transition du signal d'entrée et la transition du signal de sortie), moins de consommation d'énergie, moins de coûts et une plus grande fiabilité.

Comment utiliser la simplification booléenne pour les circuits de relais électromécaniques

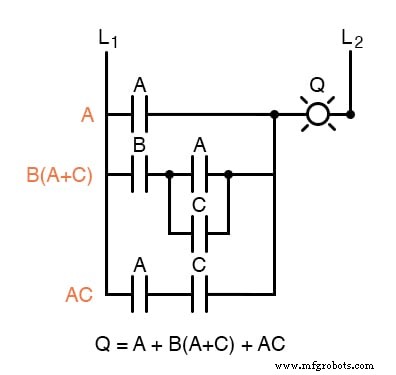
Les circuits de relais électromécaniques, généralement plus lents, consommant plus d'énergie électrique pour fonctionner, coûtant plus cher et ayant une durée de vie moyenne plus courte que leurs homologues semi-conducteurs, bénéficient considérablement de la simplification booléenne. Prenons un exemple de circuit :

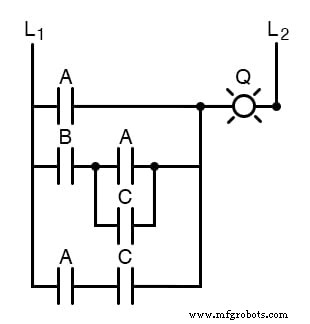
Comme précédemment, notre première étape pour réduire ce circuit à sa forme la plus simple doit être de développer une expression booléenne à partir du schéma.

Le moyen le plus simple que j'ai trouvé pour le faire est de suivre les mêmes étapes que je suivrais normalement pour réduire un réseau de résistances série-parallèle à une seule résistance totale.

Par exemple, examinez le réseau de résistances suivant avec ses résistances disposées selon le même schéma de connexion que les contacts de relais dans l'ancien circuit, et la formule de résistance totale correspondante :

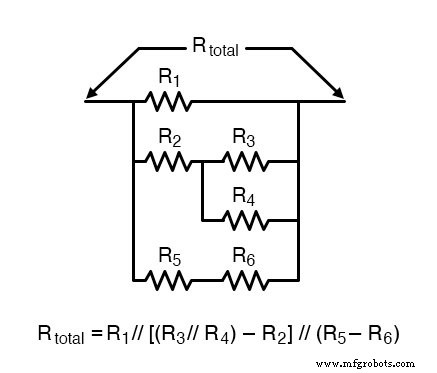
Dans la figure ci-dessus, un long tiret (—) est utilisé pour représenter la connexion en série des résistances.

N'oubliez pas que les contacts parallèles sont équivalents à l'addition booléenne, tandis que les contacts en série sont équivalents à la multiplication booléenne.

Écrivez une expression booléenne pour ce circuit de contact de relais, en suivant le même ordre de priorité que vous suivriez en réduisant un réseau de résistances série-parallèle à une résistance totale.

Il peut être utile d'écrire une sous-expression booléenne à gauche de chaque « échelon » d'échelle pour vous aider à organiser votre expression écrite :

Maintenant que nous avons une expression booléenne avec laquelle travailler, nous devons appliquer les règles de l'algèbre booléenne pour réduire l'expression à sa forme la plus simple (la plus simple étant définie comme nécessitant le moins de contacts de relais à implémenter) :

Les plus mathématiques devraient être en mesure de voir que les deux étapes employant la règle « A + AB =A » peuvent être combinées en une seule étape, la règle pouvant être étendue à :« A + AB + AC + AD + . . . =A”

Comme vous pouvez le voir, le circuit réduit est beaucoup plus simple que l'original, mais remplit la même fonction logique :

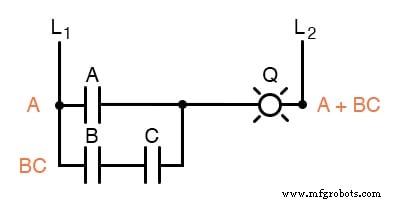
AVIS :

• Pour convertir un circuit de porte en une expression booléenne, étiquetez chaque sortie de porte avec une sous-expression booléenne correspondant aux signaux d'entrée des portes, jusqu'à ce qu'une expression finale soit atteinte à la dernière porte.
• Pour convertir une expression booléenne en circuit de porte, évaluez l'expression en utilisant l'ordre standard des opérations :la multiplication avant l'addition et les opérations entre parenthèses avant toute autre chose.
• Pour convertir un circuit logique à relais en une expression booléenne, étiquetez chaque échelon avec une sous-expression booléenne correspondant aux signaux d'entrée des contacts, jusqu'à ce qu'une expression finale soit atteinte à la dernière bobine ou lumière. Pour déterminer le bon ordre d'évaluation, traitez les contacts comme s'il s'agissait de résistances et comme si vous déterminiez la résistance totale du réseau série-parallèle formé par eux. En d'autres termes, recherchez des contacts qui sont soit directement en série ou directement en parallèle les uns avec les autres d'abord, puis « réduisez-les » en sous-expressions booléennes équivalentes avant de passer à d'autres contacts.
• Pour convertir une expression booléenne en un circuit logique à relais, évaluez l'expression en utilisant l'ordre standard des opérations :la multiplication avant l'addition et les opérations entre parenthèses avant toute autre chose.

FICHES DE TRAVAIL CONNEXES :

• Fiche de travail sur les expressions de somme de produits et de produit de somme
• Feuille de travail d'algèbre booléenne