Circuits complexes

Que faisons-nous si nous rencontrons un circuit plus complexe que les simples configurations en série que nous avons vues jusqu'à présent ? Prenons ce circuit comme exemple :

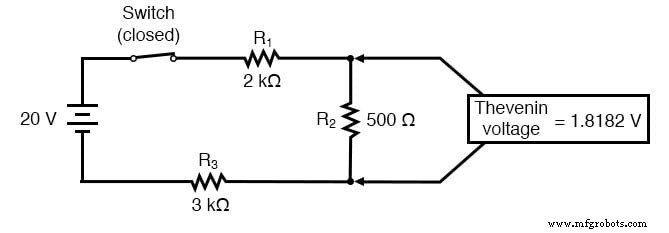
La formule de constante de temps simple (τ=RC) est basée sur une simple résistance série connectée au condensateur. D'ailleurs, la formule de constante de temps pour un circuit inductif (τ=L/R) est également basée sur l'hypothèse d'une résistance série simple. Alors, que pouvons-nous faire dans une situation comme celle-ci, où les résistances sont connectées en série-parallèle avec le condensateur (ou l'inductance) ?

Théorème de Thévenin

La réponse vient de nos études en analyse de réseau. Le théorème de Thevenin nous dit que nous pouvons réduire n'importe quel circuit linéaire à l'équivalent d'une source de tension, d'une résistance série et d'un composant de charge en quelques étapes simples. Pour appliquer le théorème de Thevenin à notre scénario ici, nous allons considérer le composant réactif (dans l'exemple de circuit ci-dessus, le condensateur) comme la charge et le retirer temporairement du circuit pour trouver la tension de Thevenin et la résistance de Thevenin.

Ensuite, une fois que nous aurons déterminé les valeurs du circuit équivalent Thevenin, nous reconnecterons le condensateur et déterminerons les valeurs de tension ou de courant au fil du temps, comme nous l'avons fait jusqu'à présent.

Après avoir identifié le condensateur comme la « charge », nous le retirons du circuit et résolvons la tension aux bornes de la charge (en supposant, bien sûr, que l'interrupteur est fermé) :

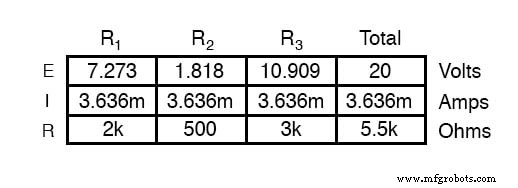
Cette étape de l'analyse nous indique que la tension aux bornes de la charge (la même que celle aux bornes de la résistance R₂ ) sera de 1,8182 volts sans charge connectée. Avec un peu de réflexion, il devrait être clair que ce sera notre tension finale aux bornes du condensateur, vu comment un condensateur complètement chargé agit comme un circuit ouvert, tirant un courant nul. Nous utiliserons cette valeur de tension pour notre tension de source de circuit équivalent Thevenin.

Maintenant, pour résoudre notre résistance Thevenin, nous devons éliminer toutes les sources d'alimentation dans le circuit d'origine et calculer la résistance vue des bornes de charge :

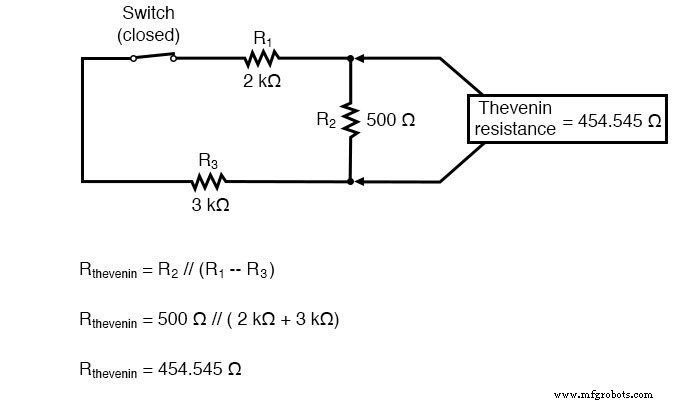
En redessinant notre circuit comme un équivalent Thevenin, nous obtenons ceci :

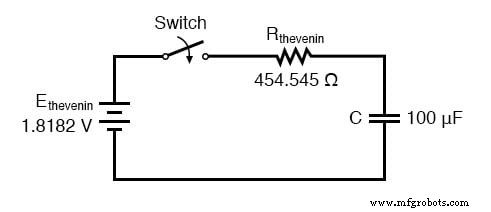
Notre constante de temps pour ce circuit sera égale à la résistance de Thevenin multipliée par la capacité (τ=RC). Avec les valeurs ci-dessus, nous calculons :

Maintenant, nous pouvons résoudre la tension aux bornes du condensateur directement avec notre formule de constante de temps universelle. Calculons pour une valeur de 60 millisecondes. Comme il s'agit d'une formule capacitive, nous allons configurer nos calculs pour la tension :

Encore une fois, parce que notre valeur de départ pour la tension du condensateur était supposée être zéro, la tension réelle aux bornes du condensateur à 60 millisecondes est égale à la quantité de changement de tension par rapport à zéro, soit 1,3325 volts.

Nous pourrions aller plus loin et démontrer l'équivalence du circuit Thevenin RC et du circuit d'origine grâce à une analyse informatique. Je vais utiliser le programme d'analyse SPICE pour démontrer ceci :