Calculs complexes de tension et de courant
Il existe des circonstances dans lesquelles vous devrez peut-être analyser un circuit réactif CC lorsque les valeurs de départ de la tension et du courant ne correspondent pas à un état complètement «déchargé». En d'autres termes, le condensateur peut démarrer à une condition partiellement chargée au lieu de démarrer à zéro volt, et un inducteur peut démarrer avec une certaine quantité de courant déjà traversé, au lieu de zéro comme nous l'avons supposé jusqu'à présent.
Prenons l'exemple de ce circuit, en commençant par l'interrupteur ouvert et en terminant par l'interrupteur en position fermée :
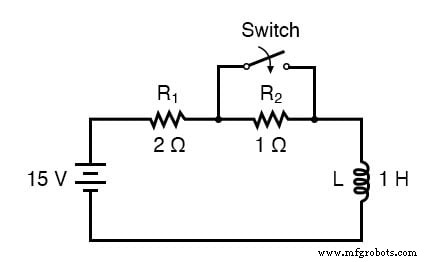
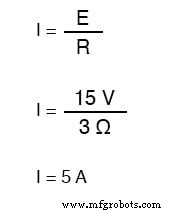
Puisqu'il s'agit d'un circuit inductif, nous commencerons notre analyse en déterminant les valeurs de début et de fin du courant . Cette étape est d'une importance vitale lors de l'analyse des circuits inductifs, comme la tension de début et de fin ne peut être connu qu'après avoir déterminé le courant ! Avec l'interrupteur ouvert (condition de démarrage), il existe une résistance totale (série) de 3 Ω, ce qui limite le courant final dans le circuit à 5 ampères :
Ainsi, avant même que l'interrupteur ne soit fermé, nous avons un courant à travers l'inducteur de 5 ampères, plutôt que de partir de 0 ampères comme dans l'exemple d'inducteur précédent. Avec l'interrupteur fermé (la condition finale), la résistance de 1 est court-circuitée (contournée), ce qui fait passer la résistance totale du circuit à 2 Ω. Avec l'interrupteur fermé, la valeur finale du courant à travers l'inducteur serait alors :
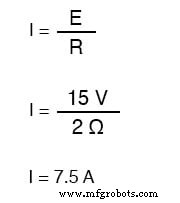
Ainsi, l'inducteur de ce circuit a un courant de démarrage de 5 ampères et un courant de fin de 7,5 ampères. Étant donné que le « timing » aura lieu pendant le temps que l'interrupteur est fermé et R2 est court-circuité, nous devons calculer notre constante de temps à partir de L1 et R1 :1 Henry divisé par 2 , soit τ =1/2 seconde. Avec ces valeurs, nous pouvons calculer ce qu'il adviendra du courant au fil du temps. La tension aux bornes de l'inducteur sera calculée en multipliant le courant par 2 (pour arriver à la tension aux bornes de la résistance de 2 Ω), puis en soustrayant cela de 15 volts pour voir ce qui reste.
Si vous vous rendez compte que la tension aux bornes de l'inducteur commence à 5 volts (lorsque l'interrupteur est fermé pour la première fois) et diminue à 0 volt au fil du temps, vous pouvez également utiliser ces chiffres pour les valeurs de début/fin dans la formule générale et obtenir les mêmes résultats :
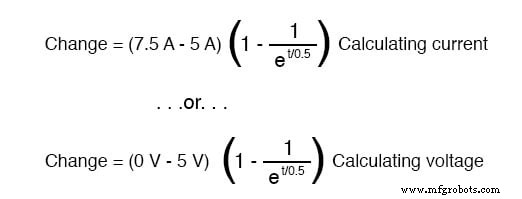
FICHES DE TRAVAIL CONNEXES :
- Feuille de travail sur les circuits à temps constant
Technologie industrielle



