Règles booléennes pour la simplification

L'algèbre booléenne trouve son utilisation la plus pratique dans la simplification des circuits logiques.

Si nous traduisons la fonction d'un circuit logique en forme symbolique (booléenne) et appliquons certaines règles algébriques à l'équation résultante pour réduire le nombre de termes et/ou d'opérations arithmétiques, l'équation simplifiée peut être retranscrite sous forme de circuit pour un circuit logique exécutant la même fonction avec moins de composants.

Si une fonction équivalente peut être obtenue avec moins de composants, le résultat sera une fiabilité accrue et un coût de fabrication réduit.

À cette fin, il existe plusieurs règles d'algèbre booléenne présentées dans cette section à utiliser pour réduire les expressions à leurs formes les plus simples.

Les identités et propriétés déjà passées en revue dans ce chapitre sont très utiles dans la simplification booléenne et, pour la plupart, présentent des similitudes avec de nombreuses identités et propriétés de l'algèbre « normale ».

Cependant, les règles présentées dans cette section sont toutes propres aux mathématiques booléennes.

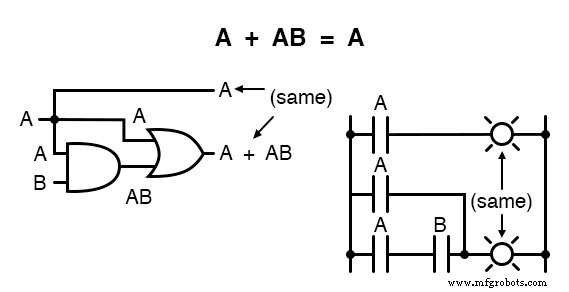
Cette règle peut être prouvée symboliquement en factorisant un « A » sur les deux termes, puis en appliquant les règles de A + 1 =1 et 1A =A pour obtenir le résultat final :

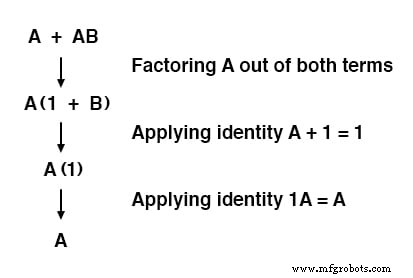
Veuillez noter comment la règle A + 1 =1 a été utilisée pour réduire le terme (B + 1) à 1.

Lorsqu'une règle comme "A + 1 =1" est exprimée à l'aide de la lettre "A", cela ne signifie pas qu'elle s'applique uniquement aux expressions contenant "A".

Ce que le « A » signifie dans une règle comme A + 1 =1 est une variable booléenne ou une collection de variables.

C'est peut-être le concept le plus difficile à maîtriser pour les nouveaux étudiants en simplification booléenne :appliquer des identités, des propriétés et des règles normalisées à des expressions qui ne sont pas sous une forme standard.

Par exemple, l'expression booléenne ABC + 1 se réduit également à 1 au moyen de l'identité « A + 1 =1 ».

Dans ce cas, nous reconnaissons que le terme « A » dans la forme standard de l'identité peut représenter l'intégralité du terme « ABC » dans l'expression d'origine.

La règle suivante ressemble à la première présentée dans cette section, mais est en fait assez différente et nécessite une preuve plus intelligente :

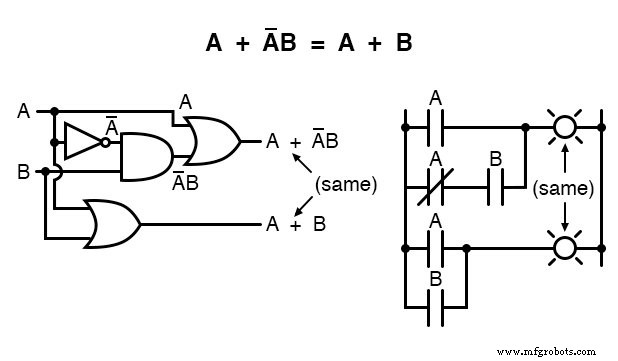
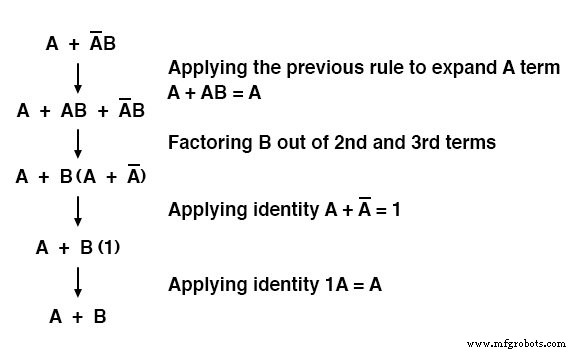
Notez comment la dernière règle (A + AB =A) est utilisée pour « dé-simplifier » le premier terme « A » dans l'expression, en changeant le « A » en un « A + AB ».

Bien que cela puisse sembler être un pas en arrière, cela a certainement aidé à réduire l'expression à quelque chose de plus simple !

Parfois, en mathématiques, nous devons faire des pas en arrière pour parvenir à la solution la plus élégante.

Savoir quand faire un tel pas et quand ne pas le faire fait partie de l'art de l'algèbre, tout comme une victoire dans une partie d'échecs nécessite presque toujours des sacrifices calculés.

Une autre règle implique la simplification d'une expression de produit de sommes :

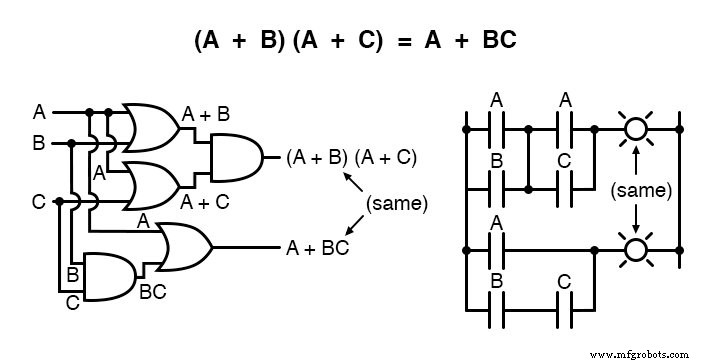
Et, la preuve correspondante :

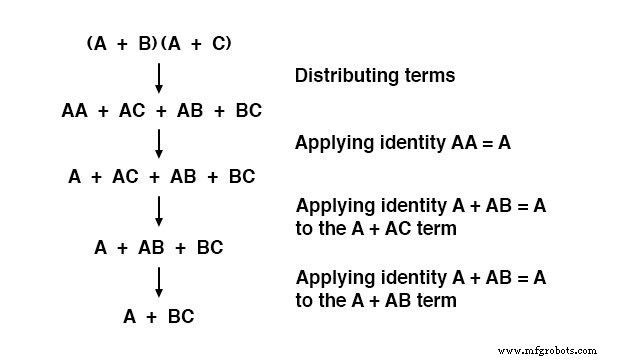
Pour résumer, voici les trois nouvelles règles de simplification booléenne exposées dans cette section :

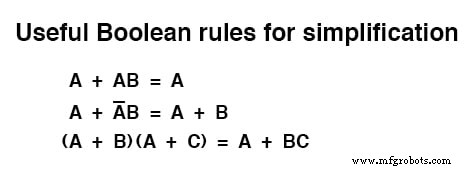
FICHES DE TRAVAIL CONNEXES :

• Feuille de travail d'algèbre booléenne