arithmétique booléenne

Commençons notre exploration de l'algèbre booléenne en additionnant des nombres :

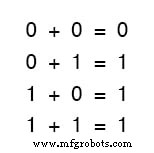
Les trois premières sommes sont parfaitement logiques pour quiconque est familiarisé avec l'addition élémentaire.

La dernière somme, cependant, est très probablement responsable de plus de confusion que toute autre déclaration en électronique numérique, car elle semble aller à l'encontre des principes de base des mathématiques.

Eh bien, cela contredit les principes d'addition pour les nombres réels, mais pas pour les nombres booléens.

Rappelez-vous que dans le monde de l'algèbre booléenne, il n'y a que deux valeurs possibles pour toute quantité et pour toute opération arithmétique :1 ou 0.

Le « 2 » n'existe pas dans le cadre des valeurs booléennes. Puisque la somme "1 + 1" n'est certainement pas 0, elle doit être 1 par élimination.

Peu importe le nombre ou le peu de termes que nous additionnons non plus. Considérez les sommes suivantes :

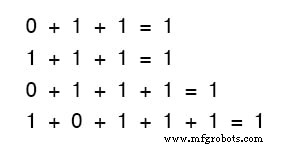
Porte OU

Examinez attentivement les sommes à deux termes du premier ensemble d'équations.

Ce modèle vous semble-t-il familier ? Cela devrait! C'est le même modèle de 1 et de 0 que celui vu dans la table de vérité pour une porte OU.

En d'autres termes, l'addition booléenne correspond à la fonction logique d'une porte « OU », ainsi qu'à des contacts de commutation en parallèle :

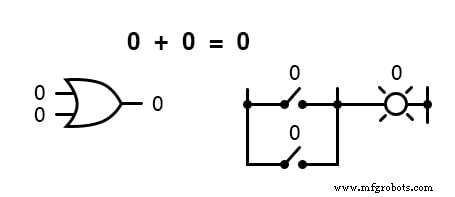
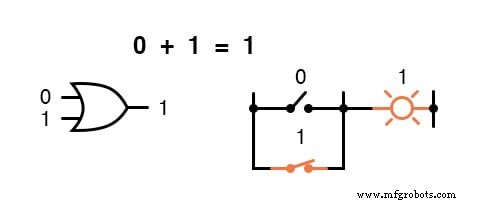
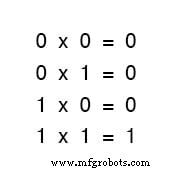
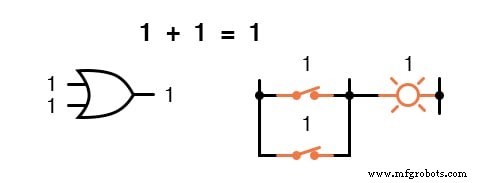
La soustraction n'existe pas dans le domaine des mathématiques booléennes.

La soustraction implique l'existence de nombres négatifs :5 - 3 est la même chose que 5 + (-3) , et en algèbre booléenne les quantités négatives sont interdites.

Il n'y a pas non plus de division en mathématiques booléennes, puisque la division n'est en réalité rien de plus qu'une soustraction composée , de la même manière que la multiplication est une addition composée .

Porte ET

La multiplication est valide en algèbre booléenne, et heureusement c'est la même chose qu'en algèbre des nombres réels :tout ce qui est multiplié par 0 est 0 , et tout ce qui est multiplié par 1 reste inchangé :

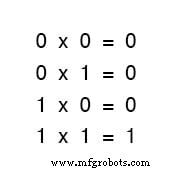
Cet ensemble d'équations devrait également vous sembler familier :c'est le même modèle trouvé dans la table de vérité pour une porte ET.

En d'autres termes, la multiplication booléenne correspond à la fonction logique d'un « ET ", ainsi qu'aux contacts de commutation en série :

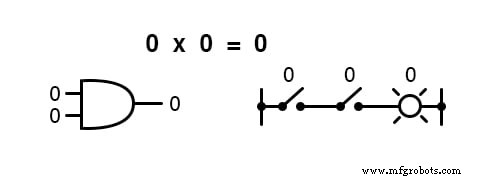
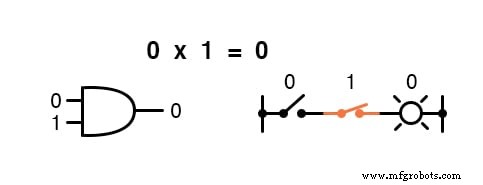
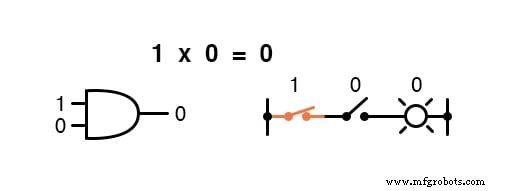
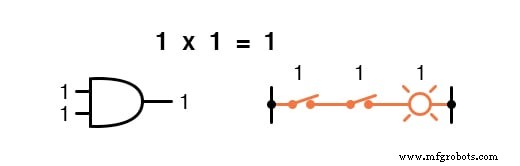
Comme l'algèbre "normale", l'algèbre booléenne utilise des lettres alphabétiques pour désigner les variables.

Contrairement à l'algèbre "normale", cependant, les variables booléennes sont toujours des majuscules, jamais des minuscules.

Parce qu'ils ne sont autorisés à posséder qu'une seule des deux valeurs possibles, soit 1 ou 0 , chaque variable a un complément :l'opposé de sa valeur.

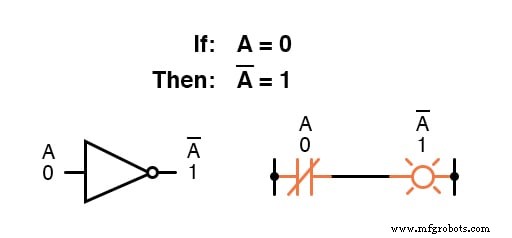
Par exemple, si la variable « A ” a une valeur de 0 , puis le complément de A a une valeur de 1 .

La notation booléenne utilise une barre au-dessus du caractère variable pour indiquer la complémentation, comme ceci :

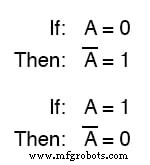
PAS de porte

Sous forme écrite, le complément de « A " noté "A-pas " ou " A-bar ”. Parfois, un symbole « premier » est utilisé pour représenter la complémentation.

Par exemple, A ’ serait le complément de A , un peu comme l'utilisation d'un symbole premier pour désigner la différenciation en calcul plutôt que la notation fractionnaire d/dt .

Habituellement, cependant, le symbole "bar" trouve une utilisation plus répandue que le "prime ", pour des raisons qui deviendront plus apparentes plus loin dans ce chapitre.

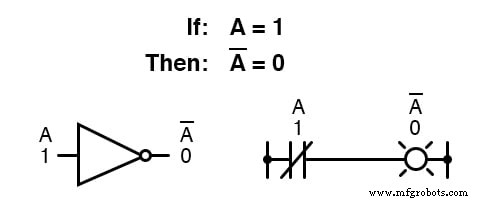
La complémentation booléenne trouve une équivalence sous la forme de la porte NON , ou un interrupteur ou contact relais normalement fermé :

La définition de base des quantités booléennes a conduit à des règles simples d'addition et de multiplication, et a exclu à la fois la soustraction et la division en tant qu'opérations arithmétiques valides.

Nous avons une symbologie pour désigner les variables booléennes, et leurs compléments. Dans la section suivante, nous allons procéder au développement des identités booléennes.

AVIS :

• L'addition booléenne est équivalente au OU fonction logique, ainsi que des contacts de commutation parallèles.
• La multiplication booléenne est équivalente au ET fonction logique, ainsi que des contacts de commutation en série.
• La complémentation booléenne est équivalente au PAS fonction logique, ainsi que normalement fermé contacts relais.

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail d'algèbre booléenne