Relations booléennes sur les diagrammes de Venn

Le quatrième exemple a A chevauchant partiellement B . Cependant, nous examinerons d'abord l'ensemble de toutes les zones hachurées ci-dessous, puis plus tard uniquement la région de chevauchement. Attribuons des expressions booléennes aux régions ci-dessus, comme indiqué ci-dessous.

En bas à gauche, il y a une zone hachurée horizontale rouge pour A . Il y a une zone hachurée verticale bleue pour B .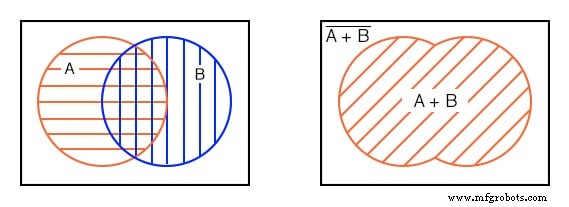

Si nous regardons la zone entière des deux, quel que soit le style de hachures, la somme totale de toutes les zones hachurées, nous obtenons l'illustration ci-dessus à droite qui correspond au OU inclus fonction de A, B. L'expression booléenne est A+B .

Ceci est indiqué par le 45 ^o zone hachurée. Tout ce qui se trouve en dehors de la zone hachurée correspond à (A+B)-pas Comme montré ci-dessus. Passons à la partie suivante du quatrième exemple.

L'autre façon de regarder un diagramme de Venn avec des cercles qui se chevauchent est de regarder uniquement la partie commune aux deux A et B , la zone hachurée en bas à gauche. L'expression booléenne de cet espace commun correspondant au ET la fonction est AB comme indiqué ci-dessous à droite. Notez que tout ce qui n'est pas à double hachure AB est AB-pas .

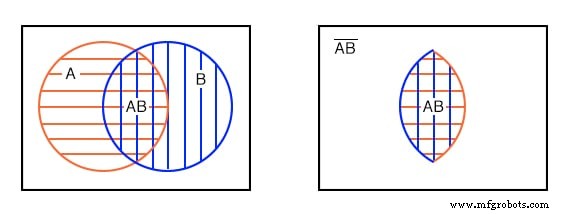
Notez que certains des membres de A , ci-dessus, sont membres de (AB)' . Certains des membres de B sont membres de (AB)' . Mais aucun des membres de (AB)' se trouvent dans la zone doublement hachurée AB .

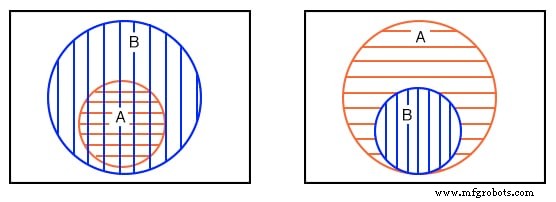
Nous avons répété le deuxième exemple ci-dessus à gauche. Votre cinquième exemple, que vous avez esquissé précédemment, est fourni ci-dessus à droite pour comparaison. Plus tard, nous trouverons l'élément occasionnel, ou le groupe d'éléments, totalement contenu dans un autre groupe dans une carte de Karnaugh.

Ensuite, nous montrons ci-dessous le développement d'une expression booléenne impliquant une variable complémentée.

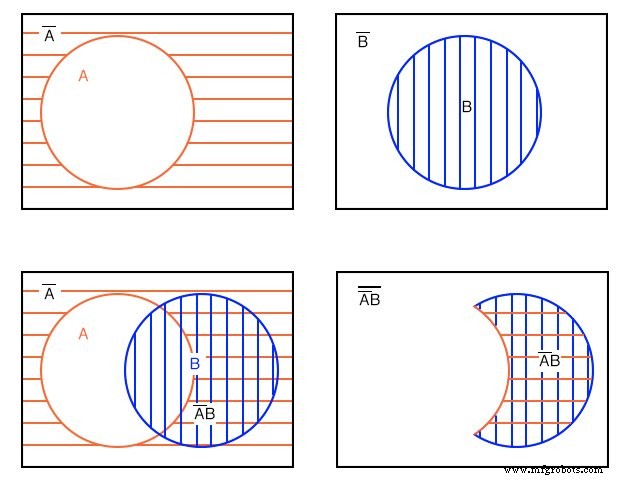
Exemple : (ci-dessus)

Afficher un diagramme de Venn pour A'B (A-pas ET B).

Solution : En commençant en haut à gauche, nous avons un A’ ombré horizontal rouge (A-pas), puis, en haut à droite, B . Ensuite, en bas à gauche, nous formons la fonction ET A'B en chevauchant les deux régions précédentes. La plupart des gens utiliseraient cela comme réponse à l'exemple posé.

Cependant, seul le A'B à double hachure est montré à l'extrême droite pour plus de clarté. L'expression A'B est la région où les deux A’ et B chevauchement. La zone claire en dehors de A'B est (A'B)' , qui ne faisait pas partie de l'exemple posé.

Essayons quelque chose de similaire avec le booléen OU fonction.

Exemple : Trouvez B'+A

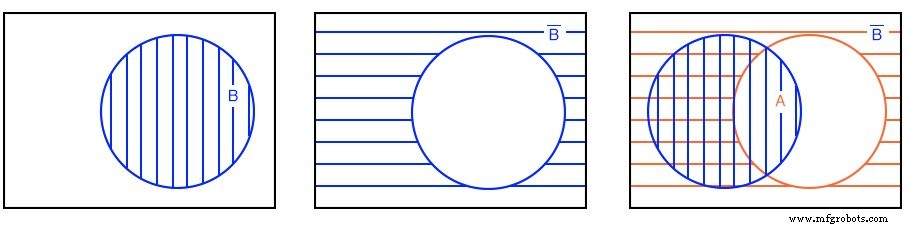
Solution : En haut à droite, nous commençons par B qui est complété par B’ . Enfin, nous superposons A au-dessus de B' . Puisque nous sommes intéressés à former le OU fonction, nous rechercherons toutes les zones hachurées quel que soit le style de hachure. Ainsi, A+B’ est toute la zone hachurée en haut à droite. Elle est représentée par une seule zone hachurée en bas à gauche pour plus de clarté.

Exemple : Rechercher (A+B’)’

Solution :

Le 45 ^o vert A+B' la zone hachurée était le résultat de l'exemple précédent. Passons à un à,(A+B’)’ ,le présent exemple, en haut à gauche, trouvons le complément de A+B’ , qui est la zone blanche claire en haut à gauche correspondant à (A+B’)’ .

Notez que nous avons répété, à droite, le AB’ résultat à double hachure d'un exemple précédent pour comparaison avec notre résultat. Les régions correspondant à (A+B’)’ et AB' ci-dessus à gauche et à droite respectivement sont identiques. Cela peut être prouvé avec le théorème de DeMorgan et la double négation.

Cela soulève un point. Les diagrammes de Venn ne prouvent en fait rien. L'algèbre booléenne est nécessaire pour les preuves formelles. Cependant, les diagrammes de Venn peuvent être utilisés pour la vérification et la visualisation. Nous avons vérifié et visualisé le théorème de DeMorgan avec un diagramme de Venn.

Exemple :

Que signifie l'expression booléenne A'+B' ressemble à un diagramme de Venn ?

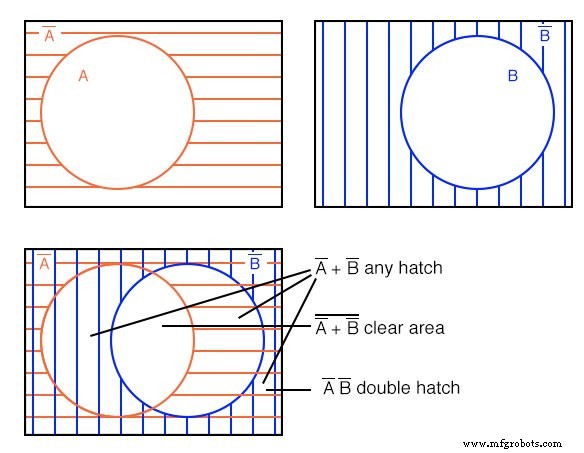
Solution : figure ci-dessus

Commencez par un A’ hachuré horizontal rouge et B’ hachuré vertical bleu au dessus. Superposez les schémas comme indiqué. On peut encore voir le A’ hachure horizontale rouge superposée à l'autre hachure. Il remplit également ce qui faisait autrefois partie du B (B-vrai) cercle, mais seulement cette partie du B cercle ouvert non commun au A cercle ouvert.

Si nous ne regardons que le B' trappe verticale bleue, elle remplit cette partie du A ouvert cercle non commun à B . Toute région avec n'importe quelle hachure, quel que soit son type, correspond à A'+B' . C'est-à-dire tout sauf l'espace blanc ouvert au centre.

Exemple :

Que signifie l'expression booléenne (A'+B')' ressemble à un diagramme de Venn ?

Solution : ci-dessus figure, en bas à gauche

En regardant l'espace blanc ouvert au centre, c'est tout PAS dans la solution précédente de A'+B' , qui est (A'+B')' .

Exemple : Montrez que (A'+B')' =AB

Solution : ci-dessous figure, en bas à gauche

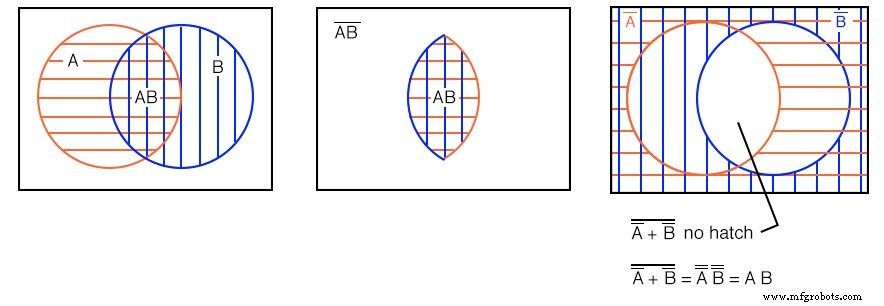
Nous avons précédemment montré sur le diagramme ci-dessus à droite que la région blanche ouverte est (A'+B')' . Sur un exemple précédent, nous avons montré une région doublement hachurée à l'intersection (superposition) de AB . Ce sont les chiffres de gauche et du milieu répétés ici.

En comparant les deux diagrammes de Venn, nous voyons que cette région ouverte , (A'+B')' , est le même que la région doublement hachurée AB (A ET B). On peut aussi prouver que (A’+B’)’=AB par le théorème de DeMorgan et la double négation comme indiqué ci-dessus.

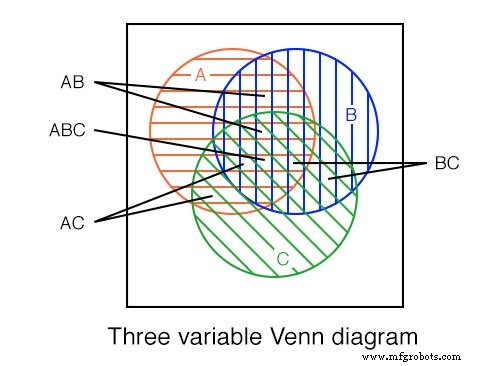
Nous montrons un diagramme de Venn à trois variables ci-dessus avec les régions A (rouge horizontal), B (bleu vertical) et, C (vert 45 ^o ). Au centre, notez que les trois régions se chevauchent et représentent l'expression booléenne ABC .

Il y a aussi une plus grande région en forme de pétale où A et B chevauchement correspondant à l'expression booléenne AB . De manière similaire A et C chevauchement produisant une expression booléenne AC . Et B et C chevauchement produisant une expression booléenne BC .

En regardant la taille des régions décrites par les expressions AND ci-dessus, nous voyons que la taille de la région varie avec le nombre de variables dans l'expression AND associée.

• Un , 1-variable est une grande région circulaire.
• AB , 2-variable est une région en forme de pétale plus petite.
• ABC , 3-variable est la plus petite région.
• Plus il y a de variables dans le terme AND, plus la région est petite.