Faire ressembler un diagramme de Venn à une carte de Karnaugh

Commençant par le cercle A dans un univers A’ rectangulaire dans la figure (a) ci-dessous, nous transformons un diagramme de Venn en presque une carte de Karnaugh.

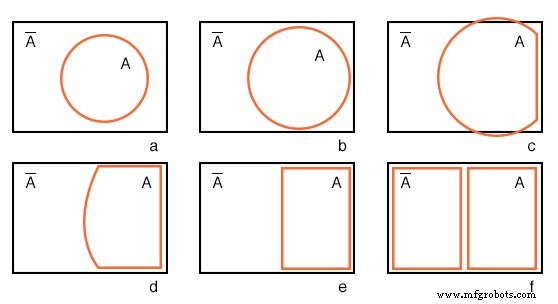
Nous élargissons le cercle A en (b) et (c), conforme à l'univers rectangulaire A’ à (d), et modifiez A à un rectangle en (e). Tout ce qui reste en dehors de A est A’ . Nous attribuons un rectangle à A’ en (f). De plus, nous n'utilisons pas d'ombrage dans les cartes de Karnaugh. Ce que nous avons jusqu'à présent ressemble à une carte de Karnaugh à 1 variable, mais est de peu d'utilité. Nous avons besoin de plusieurs variables.

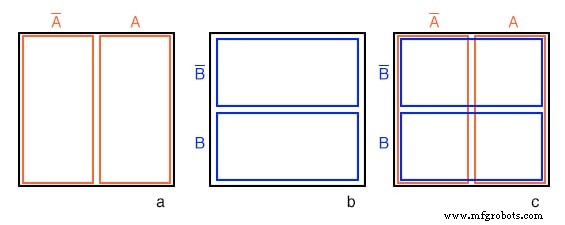
La figure (a) ci-dessus est la même que le diagramme de Venn précédent montrant A et A' ci-dessus sauf que les libellés A et A' sont au-dessus du diagramme plutôt qu'à l'intérieur des régions respectives. Imaginez que nous ayons suivi un processus similaire aux figures (a-f) pour obtenir un « diagramme de Venn carré » pour B et B' comme nous le montrons dans la figure du milieu (b).

Nous allons maintenant superposer les diagrammes des figures (a) et (b) pour obtenir le résultat en (c), tout comme nous l'avons fait pour les diagrammes de Venn. La raison pour laquelle nous faisons cela est de pouvoir observer ce qui peut être commun à deux régions qui se chevauchent, disons où A chevauche B . La cellule en bas à droite de la figure (c) correspond à AB où A chevauche B .

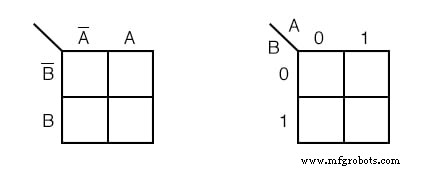
Nous ne perdons pas de temps à dessiner une carte de Karnaugh comme (c) ci-dessus, en esquissant une version simplifiée comme ci-dessus à gauche. La colonne de deux cellules sous A’ est compris comme étant associé à A’ , et le titre A est associé à la colonne de cellules en dessous. La rangée dirigée par B' est associé aux cellules à sa droite.

De manière similaire B est associé aux cellules à sa droite. Par souci de simplicité, nous ne délimitons pas les différentes régions aussi clairement qu'avec les diagrammes de Venn.

La carte de Karnaugh en haut à droite est une forme alternative utilisée dans la plupart des textes. Les noms des variables sont répertoriés à côté de la ligne diagonale.

Le A au-dessus de la diagonale indique que la variable A (et A’ ) est affecté aux colonnes. Le 0 remplace A’ , et le 1 remplace A . Le B en dessous de la diagonale est associé les lignes :0 pour B' , et 1 pour B

Exemple :

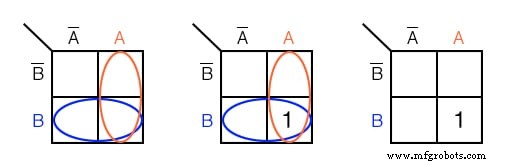
Marquez la cellule correspondant à l'expression booléenne AB dans la carte de Karnaugh ci-dessus avec un 1

Solution :

Ombrez ou encerclez la région correspondant à A . Ensuite, ombrez ou entourez la zone correspondant à B . Le chevauchement des deux régions est AB . Placez un 1 dans cette cellule. Nous ne joignons pas nécessairement le A et B régions comme ci-dessus à gauche.

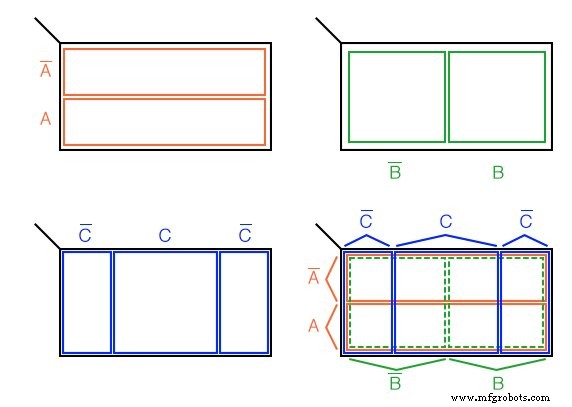
K-map à 3 variables

Nous développons une carte de Karnaugh à 3 variables ci-dessus, en commençant par les régions du type diagramme de Venn. L'univers (à l'intérieur du rectangle noir) est divisé en deux régions rectangulaires étroites et étroites pour A’ et A . Les variables B’ et B diviser l'univers en deux régions carrées. C occupe une région carrée au milieu du rectangle, avec C' divisé en deux rectangles verticaux de chaque côté du C carré.

Dans la figure finale, nous superposons les trois variables, en essayant d'étiqueter clairement les différentes régions. Les régions sont moins évidentes sans impression couleur, plus évidentes par rapport aux trois autres chiffres.

Cette K-Map à 3 variables (carte de Karnaugh) en a 2 ³ =8 cellules , les petits carrés à l'intérieur de la carte. Chaque cellule individuelle est identifiée de manière unique par les trois variables booléennes (A, B, C ). Par exemple, ABC' sélectionne de manière unique la cellule la plus à droite en bas (*), A'B'C' sélectionne la cellule la plus à gauche (x).

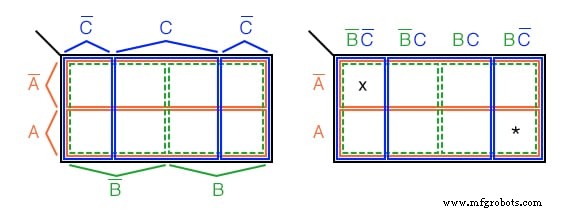
Nous n'étiquetons normalement pas la carte de Karnaugh comme indiqué ci-dessus à gauche. Bien que cette figure montre clairement la couverture de la carte par des variables booléennes uniques d'une région à 4 cellules.

Les cartes de Karnaugh sont étiquetées comme l'illustration à droite. Chaque cellule est toujours identifiée de manière unique par un terme de produit à 3 variables , un booléen ET expression. Prenez, par exemple, ABC' suivant le A ligne vers la droite et le BC' colonne vers le bas, les deux se croisant dans la cellule inférieure droite ABC' . Voir (*) figure ci-dessus.

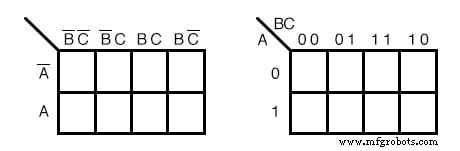
Les deux formes différentes ci-dessus d'une carte de Karnaugh à 3 variables sont équivalentes et constituent la forme finale qu'elle prend. La version à droite est un peu plus facile à utiliser, car nous n'avons pas à écrire autant d'en-têtes alphabétiques booléens et de barres de complément, juste des 1 et des 0 Utilisez la forme de carte à droite et recherchez celle de gauche dans certains textes . Les en-têtes de colonne à gauche B’C’, B’C, BC, BC’ équivalent à 00, 01, 11, 10 sur la droite. Les en-têtes de ligne A, A' sont équivalents à 0, 1 sur la bonne carte.