Cartes de Karnaugh, tables de vérité et expressions booléennes

Qui a développé la carte de Karnaugh ?

Maurice Karnaugh, ingénieur en télécommunications, a développé la carte de Karnaugh aux Bell Labs en 1953 tout en concevant des circuits de commutation téléphonique basés sur la logique numérique.

L'utilisation de la carte de Karnaugh

Maintenant que nous avons développé la carte de Karnaugh à l'aide des diagrammes de Venn, mettons-la à profit. Karnaugh mappe réduire la logique fonctionne plus rapidement et plus facilement par rapport à l'algèbre booléenne. Par réduire, nous entendons simplifier, en réduisant le nombre de portes et d'entrées.

Nous aimons simplifier la logique à un coût le plus bas forme pour réduire les coûts par l'élimination des composants. Nous définissons le coût le plus bas comme étant le plus petit nombre de portes avec le plus petit nombre d'entrées par porte.

Lorsqu'ils ont le choix, la plupart des étudiants font une simplification logique avec des cartes de Karnaugh plutôt qu'avec l'algèbre booléenne une fois qu'ils ont appris cet outil.

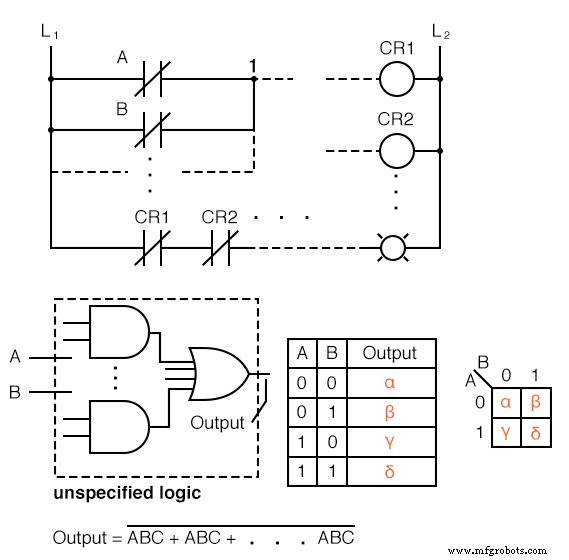
Nous montrons cinq éléments individuels ci-dessus, qui ne sont que des manières différentes de représenter la même chose :une fonction logique numérique arbitraire à 2 entrées. Il y a d'abord la logique à relais, puis les portes logiques, une table de vérité, une carte de Karnaugh et une équation booléenne.

Le fait est que tous ces éléments sont équivalents. Deux entrées A et B peut prendre les valeurs 0 ou 1 , haut ou bas, ouvert ou fermé, Vrai ou Faux, selon le cas. Il y en a 2 ² =4 combinaisons d'entrées produisant une sortie. Ceci s'applique aux cinq exemples.

Ces quatre sorties peuvent être observées sur une lampe dans la logique à relais du relais, sur une sonde logique sur le schéma de la porte. Ces sorties peuvent être enregistrées dans la table de vérité ou dans la carte de Karnaugh. Regardez la carte de Karnaugh comme étant une table de vérité réorganisée.

La sortie de l'équation booléenne peut être calculée par les lois de l'algèbre booléenne et transférée à la table de vérité ou à la carte de Karnaugh.

Laquelle des cinq descriptions logiques équivalentes devrions-nous utiliser ? Celui qui est le plus utile pour la tâche à accomplir.

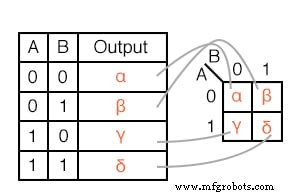
Les sorties d'une table de vérité correspondent un à un aux entrées de la carte de Karnaugh. En partant du haut de la table de vérité, les entrées A=0, B=0 produisent une sortie .

Notez que cette même sortie se trouve dans la carte de Karnaugh à l'adresse de cellule A=0, B=0, coin supérieur gauche de la K-map où la ligne A=0 et la colonne B=0 se croisent. Les autres sorties de table de vérité β, χ, δ des entrées AB=01, 10, 11 se trouvent aux emplacements K-map correspondants.

Ci-dessous, nous montrons les régions adjacentes à 2 cellules dans la carte K à 2 variables à l'aide du diagramme de Venn rectangulaire précédent comme les régions booléennes.

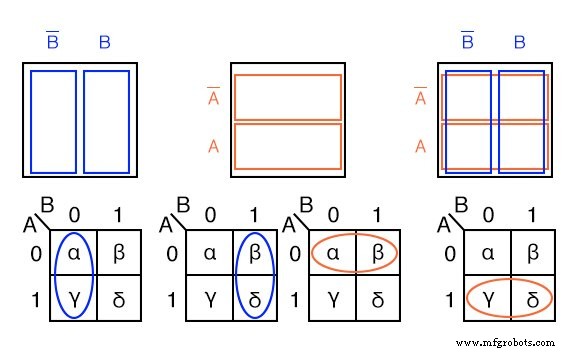
Les cellules α et χ sont adjacentes dans la K-map sous forme d'ellipses dans la K-map la plus à gauche ci-dessous. En se référant à la table de vérité précédente, ce n'est pas le cas. Il y a une autre entrée de la table de vérité (β) entre eux. Ce qui nous amène à l'essentiel de l'organisation de la K-map dans un tableau carré, les cellules avec des variables booléennes en commun doivent être proches les unes des autres afin de présenter un motif qui nous saute aux yeux.

Pour les cellules α et χ ils ont la variable booléenne B’ en commun. Nous le savons parce que B=0 (identique à B' ) pour la colonne au-dessus des cellules α et χ. Comparez cela au diagramme de Venn carré au-dessus de la K-map.

Un raisonnement similaire montre que β et ont un booléen B (B=1) en commun. Alors, et β ont booléen A’ (A=0) en commun. Enfin, χ et ont un booléen A (A=1) en commun. Comparez les deux dernières cartes au diagramme de Venn carré du milieu.

Pour résumer, nous recherchons la similitude des variables booléennes entre les cellules. La carte de Karnaugh est organisée de manière à ce que nous puissions voir cette similitude. Essayons quelques exemples.

Exemples

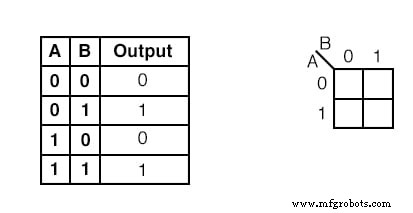
Exemple :

Transférez le contenu de la table de vérité sur la carte de Karnaugh ci-dessus.

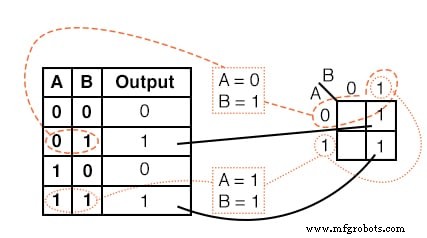
Solution :

La table de vérité contient deux 1 s. la K-map doit avoir les deux. localisez le premier 1 dans la 2ème ligne de la table de vérité ci-dessus.

• notez l'adresse AB de la table de vérité
• localisez la cellule dans la K-map ayant la même adresse
• placez un 1 dans cette cellule

Répétez le processus pour le 1 dans la dernière ligne de la table de vérité.

Exemple :

Pour la carte de Karnaugh dans le problème ci-dessus, écrivez l'expression booléenne. La solution est ci-dessous.

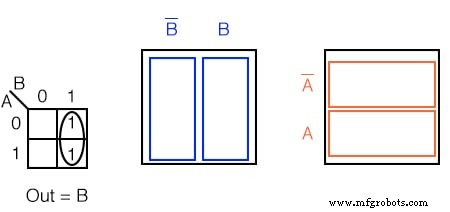
Solution :

Recherchez les cellules adjacentes, c'est-à-dire au-dessus ou sur le côté d'une cellule. Les cellules diagonales ne sont pas adjacentes. Les cellules adjacentes auront une ou plusieurs variables booléennes en commun.

• Regroupez (encerclez) les deux 1 s dans la colonne
• Trouvez la ou les variables top et/ou side qui sont les mêmes pour le groupe, écrivez ceci comme résultat booléen. C'est B dans notre cas.
• Ignorer les variables qui ne sont pas les mêmes pour un groupe de cellules. Dans notre cas, A varie, vaut à la fois 1 et 0, ignorez le booléen A.
• Ignorez toute variable non associée aux cellules contenant des 1. B' n'a personne en dessous. Ignorer B'
• Résultat Sortie =B

Cela pourrait être plus facile à voir en comparant aux diagrammes de Venn à droite, en particulier le B colonne.

Exemple :

Écrivez l'expression booléenne pour la carte de Karnaugh ci-dessous.

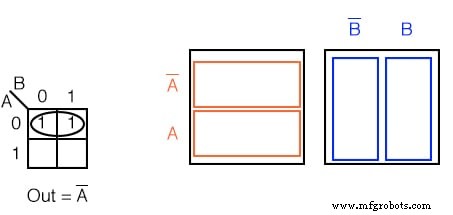
Solution : (ci-dessus)

• Regroupez (encerclez) les deux 1 dans la rangée
• Recherchez la ou les variables qui sont les mêmes pour le groupe, Out =A’

Exemple :

Pour la table de vérité ci-dessous, transférez les sorties vers le Karnaugh, puis écrivez l'expression booléenne pour le résultat.

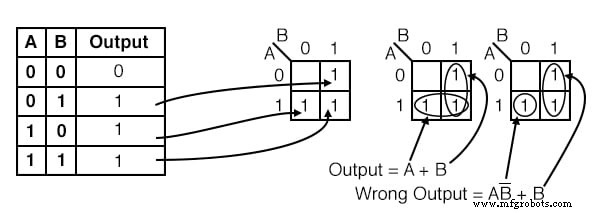
Solution :

Transférez le 1 s des emplacements dans la table de vérité aux emplacements correspondants dans la K-map.

• Regroupez (encerclez) les deux 1 dans la colonne sous B=1
• Regroupez (encerclez) les deux 1 dans la rangée à droite de A=1
• Écrire le terme de produit pour le premier groupe =B
• Écrivez le terme de produit pour le deuxième groupe =A
• Écrivez la somme des produits des deux termes ci-dessus Sortie = A+B

La solution de la K-map du milieu est la solution la plus simple ou la moins chère. Une solution moins souhaitable se trouve à l'extrême droite. Après avoir regroupé les deux 1 s, nous commettons l'erreur de former un groupe de 1 cellule. La raison pour laquelle ce n'est pas souhaitable est que :

• La cellule unique a un terme de produit de AB’
• La solution correspondante est Sortie =AB' + B
• Ce n'est pas la solution la plus simple

La façon de récupérer ce single 1 est de former un groupe de deux avec le 1 à droite de celui-ci comme indiqué dans la ligne inférieure de la K-map du milieu, même si ce 1 a déjà été inclus dans le groupe de colonnes (B ). Nous sommes autorisés à réutiliser les cellules afin de former des groupes plus importants. En fait, c'est souhaitable car cela conduit à un résultat plus simple.

Nous devons souligner que l'une ou l'autre des solutions ci-dessus, Sortie ou Sortie incorrecte, est logiquement correcte. Les deux circuits donnent la même sortie. Il s'agit de l'ancien circuit étant la solution la moins chère.

Exemple :

Remplissez la carte de Karnaugh pour l'expression booléenne ci-dessous, puis écrivez l'expression booléenne pour le résultat.

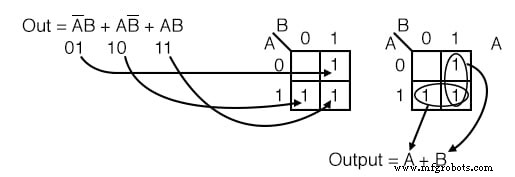
Solution : (ci-dessus)

L'expression booléenne a trois termes de produit. Il y aura un 1 saisie pour chaque terme de produit. Bien que, en général, le nombre de 1 s par terme de produit varie avec le nombre de variables dans le terme de produit par rapport à la taille de la K-map.

Le terme produit est l'adresse de la cellule où le 1 est saisi. Le premier terme du produit, A'B , correspond au 01 cellule sur la carte. Un 1 est inscrit dans cette cellule. Les deux autres termes P sont saisis pour un total de trois 1

Ensuite, procédez au regroupement et à l'extraction du résultat simplifié comme dans le problème précédent de la table de vérité.

Exemple :

Simplifiez le schéma logique ci-dessous.

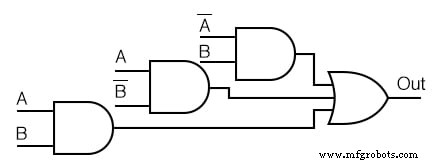
Solution : (Figure ci-dessous)

• Écrivez l'expression booléenne pour le diagramme logique d'origine comme indiqué ci-dessous
• Transférer les conditions du produit sur la carte de Karnaugh
• Former des groupes de cellules comme dans les exemples précédents
• Écrivez une expression booléenne pour les groupes comme dans les exemples précédents
• Dessiner un schéma logique simplifié

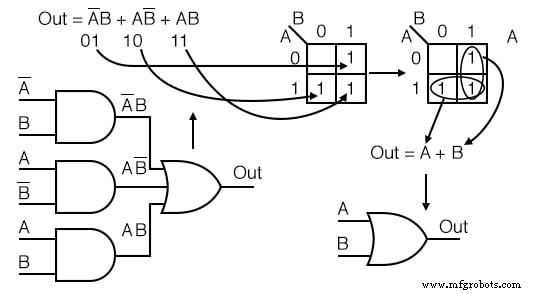
Exemple : Simplifiez le schéma logique ci-dessous.

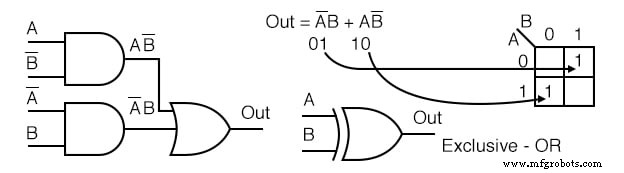
Solution :

• Écrivez l'expression booléenne pour le schéma logique d'origine illustré ci-dessus
• Transférez les termes du produit sur la carte de Karnaugh.
• Il n'est pas possible de former des groupes.
• Aucune simplification n'est possible ; laissez-le tel quel.

Aucune simplification logique n'est possible pour le schéma ci-dessus. Cela arrive parfois. Ni les méthodes des cartes de Karnaugh ni l'algèbre booléenne ne peuvent simplifier davantage cette logique.

Nous montrons ci-dessus un symbole schématique OU exclusif ; cependant, il ne s'agit pas d'une simplification logique. Cela rend simplement un diagramme schématique plus joli.

Puisqu'il n'est pas possible de simplifier la logique OU-Exclusif et qu'elle est largement utilisée, elle est fournie par les fabricants en tant que circuit intégré de base (7486).

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail de cartographie de Karnaugh
• Feuille de travail d'algèbre booléenne
• Feuille de travail des portes logiques de base