Propriétés algébriques booléennes
Un autre type d'identité mathématique, appelé « propriété » ou « loi », décrit comment différentes variables sont liées les unes aux autres dans un système de nombres.
La propriété commutative
L'une de ces propriétés est connue sous le nom de propriété commutative , et cela s'applique également à l'addition et à la multiplication.
En substance, la propriété commutative nous dit que nous pouvons inverser l'ordre des variables qui sont soit additionnées, soit multipliées sans changer la vérité de l'expression :
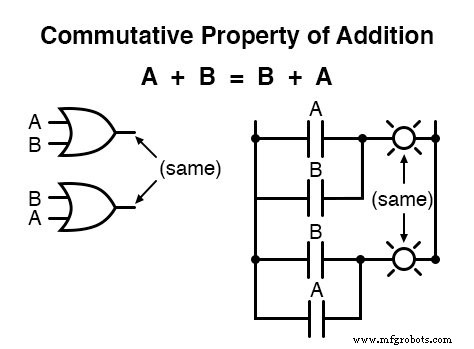
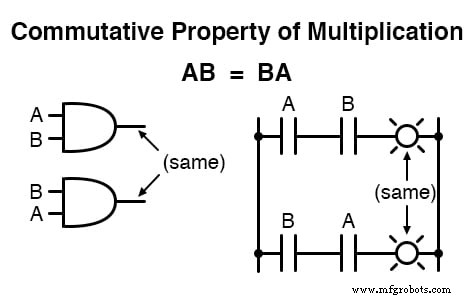
La propriété associative
En plus des propriétés commutatives d'addition et de multiplication, nous avons la propriété associative , s'appliquant à nouveau aussi bien à l'addition et à la multiplication.
Cette propriété nous dit que nous pouvons associer des groupes de variables ajoutées ou multipliées avec des parenthèses sans altérer la vérité des équations.
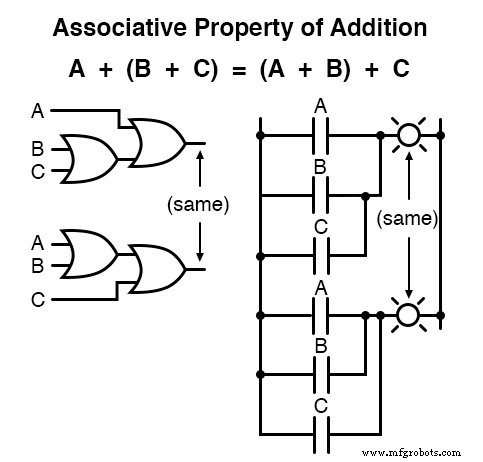
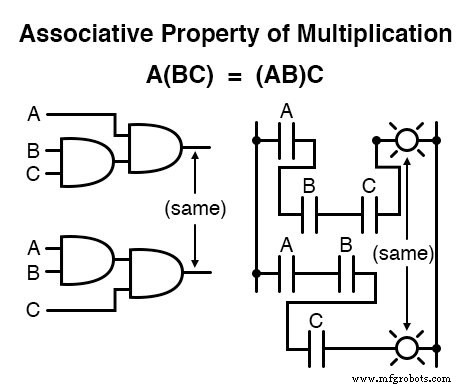
La propriété distributive
Enfin, nous avons la propriété distributive , illustrant comment développer une expression booléenne formée par le produit d'une somme, et à l'inverse nous montre comment les termes peuvent être factorisés hors des sommes-de-produits booléens :
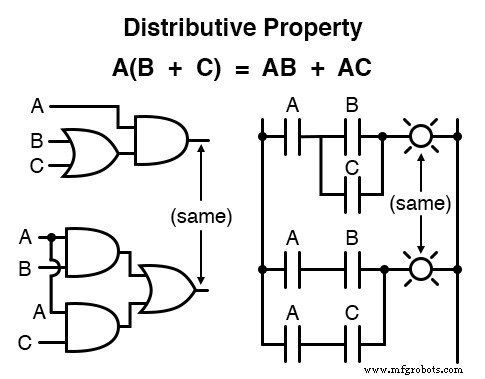
Pour résumer, voici les trois propriétés de base :commutative, associative et distributive.

FICHES DE TRAVAIL CONNEXES :
- Feuille de travail d'algèbre booléenne
Technologie industrielle



