Monocouches SnxPy :un nouveau type de matériaux bidimensionnels à haute stabilité, mobilité des porteurs et propriétés magnétiques

Introduction

Les composés binaires bidimensionnels (2D) ont attiré une grande attention ces dernières années en raison de leurs propriétés uniques et peuvent fournir des conseils fiables pour leurs applications potentielles dans la nanoélectronique et les dispositifs optoélectroniques [1]. Par exemple, le graphène a suscité un grand intérêt depuis sa découverte en raison de ses propriétés et de ses applications potentielles [2,3,4,5,6], alors que le graphène a une petite bande interdite indétectable à température ambiante, ce qui le rend difficile à utiliser dans les nanodispositifs optoélectroniques. Ainsi, ces difficultés ont incité les chercheurs à se résoudre à trouver des matériaux 2D avec une bande interdite idéale. Dans les années suivantes, le nitrure de bore (BN) [7], MoS₂ ou d'autres dichalcogénures de métaux de transition [8,9,10,11,12,13], et des trichalcogénures de métaux de transition [14, 15], entre autres, sortent. Ces dernières années, le graphène et d'autres matériaux 2D du groupe IV (silicone, stanène et germanène [16]) ont fait de bons progrès dans la recherche scientifique. Sauf que les matériaux semi-conducteurs 2D appartenant au groupe V, en particulier le phosphorène [17,18,19] et l'arsenène [20], émergent comme une nouvelle génération de prétendants dans le domaine des dispositifs optoélectroniques. Le phosphène a de larges perspectives d'application dans les transistors à effet de champ, les dispositifs optoélectroniques, la spintronique, les capteurs de gaz et les cellules solaires, etc., tandis que le stanène, une structure en nid d'abeille 2D, est considéré comme un nouveau type de matériau avec des propriétés physiques supérieures après le graphène en raison de son fort couplage spin-orbital des électrons.

Il est urgent de synthétiser deux types d'éléments pour obtenir de nouveaux matériaux 2D multifonctionnels. Il est rapporté que l'alliage est souvent utilisé pour améliorer les propriétés des matériaux 2D afin d'étendre son applicabilité. Par exemple, MoS 2D_2x Se_{2(1 − x )} et WS_2x Se_{2(1 − x )} les nanofeuillets [21, 22] témoignent de propriétés étranges telles que des propriétés électroniques et optiques accordables et un rapport de Poisson négatif dans le plan avec x /y (1/1, 1/2, 1/3, etc.) numéro de coordination. Pour un autre exemple, le matériau d'alliage 2D Si_x C_y [23], B_x C_y [24], et B_x Si_y [25] montrent de nombreuses caractéristiques nouvelles (structure de dernière génération, propriétés électroniques et mécaniques) par le calcul des premiers principes qui sont différentes de celles de l'état fondamental pur. Étant donné que les monocouches de phosphore et de stanène 2D ont de nouvelles propriétés, les éléments Sn et P ont été composés avec diverses stoechiométries.

Dans ce travail, nous avons construit quelques structures par l'algorithme d'optimisation d'essaim de particules (PSO). Ensuite, nous avons distingué les quatre structures les plus stables de 2D Sn_x P_y monocouches avec différents nombres de coordination et étudié les propriétés électroniques sur la base de l'optimisation de la théorie fonctionnelle de la densité (DFT). Les structures de bandes électroniques calculées suggèrent que toutes les monocouches stables ou métastables avec des nombres de coordination différents sont des semi-conducteurs avec une bande interdite indirecte. Plus important encore, le Pmc2₁ -SnP₂ La monocouche est un semi-conducteur de type gap direct avec une bande interdite finie de 0,92 eV dans la région de la lumière infrarouge. Mais au-delà, le Pmc2₁ -SnP₂ la structure est un semi-conducteur de type gap direct qui possède une mobilité électronique élevée de ∼ 800 cm ² V ⁻¹ s ⁻¹ , ce qui est bien supérieur à celui de MoS₂ (∼ 200 cm ² V ⁻¹ s ⁻¹ ). La monocouche de P\( \overline{4}{2}_1 \)m-SnP₂ structure avec une structure de bande de valence unique peut passer de non magnétique à ferromagnétique par le dopage des trous en raison du « critère de Stoner ». Les structures de bandes électroniques calculées suggèrent que toutes les monocouches de Sn_x P_y sont des semi-conducteurs avec des bandes interdites réglables de manière flexible sous la contrainte biaxiale, permettant l'ingénierie des contraintes de quatre structures de bandes interdites dans presque toute la plage de lumière visible.

Méthodes de calcul

Afin de garantir une recherche approfondie de la diversité structurelle, divers x et y la sélection de un à six sont prises en compte sur la base de l'algorithme d'optimisation de l'essaim de particules (PSO) [26]. Les résultats de la recherche livrés les structures monocouches sont relativement stables uniquement pour y /x 1.

Pour étudier la structure électronique de Sn_x 2D P_y monocouches avec un nombre de coordination différent, nos calculs ont été effectués en utilisant la méthode de la théorie fonctionnelle de la densité d'ondes planes (DFT) [27, 28] à réaliser dans le Vienna Ab-initio Simulation Package (VASP) [29, 30, 31]. Grâce à l'approximation du gradient généralisé (GGA) pour décrire l'énergie d'échange-corrélation sous la forme de Per-dew-Burke-Ernzerhof (PBE) [32,33,34,35] et le potentiel électron-ion est décrit par l'amplification de projection méthode des vagues [33]. L'énergie de coupure de l'onde plane a été choisie pour être une énergie de 500  eV pour Sn_x P_y systèmes, respectivement. Un point k suffisamment dense (9 × 9 × 1) de l'espace réciproque a été échantillonné dans la zone de Brillouin. L'espace vide perpendiculaire au plan entre les super-cellules voisines est supérieur à 25 Å, éliminant l'interaction entre les réplications. Dans le calcul en deux étapes consécutives, il est défini sur 10 ⁵ eV comme valeur de convergence énergétique. Lors de l'optimisation géométrique, les forces atomiques de toutes les structures sont inférieures à 0,02 eV Å ⁻¹ en utilisant la méthode du gradient conjugué jusqu'à ce que les atomes atteignent leur position optimale. De plus, nous utiliserons la supercellule avec 4 × 4 × 1 pour le calcul de dynamique moléculaire ab initio (AIMD) lorsque l'algorithme Nosé [36] à 300K.

La mobilité des porteurs est principalement affectée par la diffusion des ondes latérales acoustiques, la diffusion des ondes latérales optiques et la diffusion des impuretés ionisées. Étant donné que ces deux derniers n'ont pas autant d'influence que le premier, la mobilité que nous avons calculée inclut la mobilité sous la diffusion des ondes acoustiques latérales. La mobilité affecte principalement deux performances des transistors :l'une est que la concentration en porteurs détermine ensemble la conductivité (l'inverse de la résistivité) du matériau semi-conducteur. Deuxièmement, cela affecte la fréquence de travail de l'appareil. La principale limitation des caractéristiques de réponse en fréquence des transistors bipolaires est le temps nécessaire aux porteurs minoritaires pour traverser la région de base. La mobilité est un paramètre important pour mesurer la conductivité des matériaux semi-conducteurs 2D. Il détermine la conductivité des matériaux semi-conducteurs et affecte la vitesse de fonctionnement des appareils. Ainsi, la mobilité des porteurs est contrôlée par la dispersion des phonons et peut être décrite par la théorie du potentiel de déformation (DP) proposée par Bardeen et Shockley [37]. Ainsi, la mobilité du porteur dans les matériaux 2D peut être exprimée par [38, 39]

où e , et k _B sont respectivement les constantes de Planck et de Boltzmann à charge électronique réduite. Et T est la température qui s'est fixée à 300K. Où m* est la masse effective, E ₁ est la constante de potentiel de déformation, et C ^2D est la rigidité dans le plan.

L'effet linéaire du système sur le champ lumineux sous le vecteur de petite onde est déterminé par la partie imaginaire de la constante diélectrique complexe et la fonction diélectrique qui peut être calculée par

où le ε ₁ (ω ) et ε ₂ (ω ) sont la partie réelle de la fonction et la partie imaginaire, ε ₁ (ω ) peut dériver de la partie imaginaire ε ₂ (ω ) la fonction diélectrique de Kramer-Kronig peut être exprimée [40]. La partie imaginaire de la fonction diélectrique peut être exprimée sous la forme

De plus, le coefficient d'absorption I (ω ) a été obtenu par

où le C est la bande de conduction, le V est les états de la bande de valence, Ω est le volume de cellule unitaire, m est la masse des électrons libres, e est la charge des électrons libres, et ω est la fréquence des photons incidents.

Résultats et discussion

Stabilité

Tout d'abord, quatre Sn_x 2D P_y monocouches ont été considérées pour déterminer leurs stabilités énergétiques. L'énergie de formation est un paramètre énergétique dans un système thermodynamique qui est un point clé pour vérifier la stabilité du système. La stabilité relative de Sn_x P_y les monocouches peuvent être confirmées en calculant l'énergie de formation et sont calculées comme

où E est l'énergie d'un composé ou d'un élément constitutif à une pression spécifique. N est le nombre d'atomes dans la maille élémentaire. L'énergie de formation négative du système calculé indique que la configuration est stable ou métastable [41]. Les énergies de formation calculées de Sn_x P_y les monocouches sont de − 0,235, − 0,223, − 0,159 et − 0,016 eV/atome (indiquées dans le tableau 1), respectivement. Selon sa définition, une valeur plus petite indique une stabilité plus élevée. De toute évidence, P\( \overline{6} \)m2-SnP est la plus stable de ces quatre structures. Plus particulièrement, la stabilité thermique élevée des matériaux semi-conducteurs est particulièrement importante dans l'application des dispositifs électroniques. Ici, la stabilité thermique du Sn_x P_y monocouches examinées à l'aide de simulations de dynamique moléculaire ab initio (AIMD). Sur la base des symétries des groupes spatiaux, on calcule juste la stabilité de P\( \overline{6} \)m2-SnP pour des structures similaires P\( \overline{6} \)m2-SnP et Pmc2₁ -SnP₂ et Pmc2₁ -SnP₂ pour Pmc2₁ -SnP₂ et P\( \overline{4}{2}_1 \)m-SnP₂ structure. Les résultats indiquent que la valeur moyenne de l'énergie totale de la structure reste presque inchangée et que la structure reste inchangée après 1 ps, 3 ps et 5 ps, suggèrent que Sn_x P_y les monocouches sont thermiquement stables (sur la figure S1). Ensuite, nous avons calculé les courbes de dispersion des phonons et n'avons pas de fréquences vibrationnelles imaginaires, ce qui implique que les structures sont dynamiquement stables (sur la figure S1). Plusieurs méthodes ont été rapportées dans la littérature pour synthétiser des matériaux stratifiés, notamment le clivage micromécanique [2], la croissance épitaxiale [42], le dépôt chimique en phase vapeur [43] et l'exfoliation liquide [44]. Certains matériaux de structure similaire ont été préparés expérimentalement avec succès. Nous avons trouvé des rapports connexes selon lesquels peu de couches de nanofeuillets de GaSe ont été transformées en un photodétecteur haute performance dans l'expérience [45]. De plus, la préparation, l'isolement et la caractérisation rapide et sans ambiguïté de couches ultrafines de grande taille de MoS₂ , GaS et GaSe déposés sur SiO₂ Les substrats /Si sont signalés [46].

Comme représenté sur la figure 1a, b, les structures de P\( \overline{3} \)m1-SnP présentent une structure similaire à la phase hexagonale P\( \overline{6} \)m2-SnP. Le Pmc2₁ -SnP ₂ phase trigonale (Fig. 1c) montre que le x /y la composition est encore augmentée à 1/2. Le matériau d'une structure similaire à P\( \overline{4} \)2₁ m-SnP₂ a été prouvée stable par le calcul théorique [47]. De plus, une nouvelle étude trouve la structure de XY₂ (Fig. 1d) est un semi-conducteur à bande interdite indirecte, et il peut être sensible aux champs électriques et aux contraintes. Nous pensons que le matériel que nous prévoyons aura une préparation réussie à l'avenir avec le développement de la technologie.

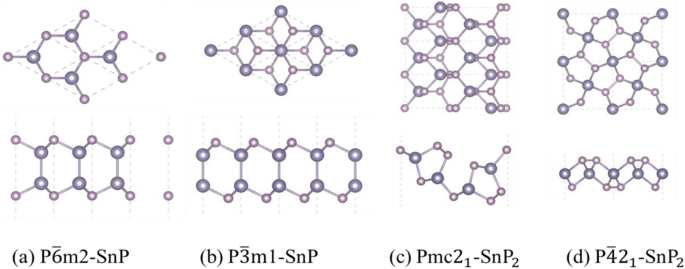
Vues de dessus et de côté des structures atomiques de Sn_x P_y monocouches :a P\( \overline{6} \)m2-SnP, b P\( \overline{3} \)m1-SnP, c Pmc2₁ -SnP₂ , et d P\( \overline{4}{2}_1 \)m-SnP₂; le niveau de Fermi (ligne pointillée horizontale) est décalé à 0 eV. Les sphères roses épaisses représentent les atomes Sn et les sphères rose clair représentent les atomes P

Propriétés électroniques et magnétiques

Les structures de bandes calculées et la densité partielle d'états de Sn_x P_y les monocouches sont tracées sur la figure 2. Comme le montre la figure 2a, le P6̅m2-SnP est un semi-conducteur indirect avec une bande interdite de 1,19 eV. Le maximum de bande de valence (VBM) dans la direction Γ → K est apporté par les orbitales hybrides Sn-p et P-p, tandis que le minimum de bande de conduction (CBM) au point K dérive des orbitales hybrides Sn-s et P-p. P\( \overline{3} \)m1-SnP présente des structures de bandes électroniques similaires à celles de P\( \overline{6} \)m2-SnP mais avec une bande interdite plus petite de 1,21 eV. La dispersion de la bande de valence de P\( \overline{6} \)m2-SnP et P\( \overline{3} \)m1-SnP près du point Γ et du niveau de Fermi (E _F ) est assez plat, étant donné la densité d'états assez élevée (DOS) et une singularité de van Hove autour du VBM. Le Pmc2₁ -SnP₂ présente un caractère semi-conducteur de type gap direct (E _g (direct) − E _g (indirect) =6 meV) avec une bande interdite de 0,72 eV (voir Fig. 2c). Son VBM est principalement attribué aux orbitales P-p, tandis que son CBM est principalement dû aux orbitales P-p et Sn-s. Le P\( \overline{4}{2}_1 \)m -SnP₂ est un semi-conducteur à espace indirect avec un E _g de 1,79  eV, et les bandes dérivent de s'apparente à la figure 2c. Plus important encore, P\( \overline{4}{2}_1 \)m-SnP₂ monocouche a une condition similaire à celle de la figure 2a, b, un caractère de dispersion à bande plate autour du VBM apparaît également, entraînant un DOS très élevé et une singularité de van Hove.

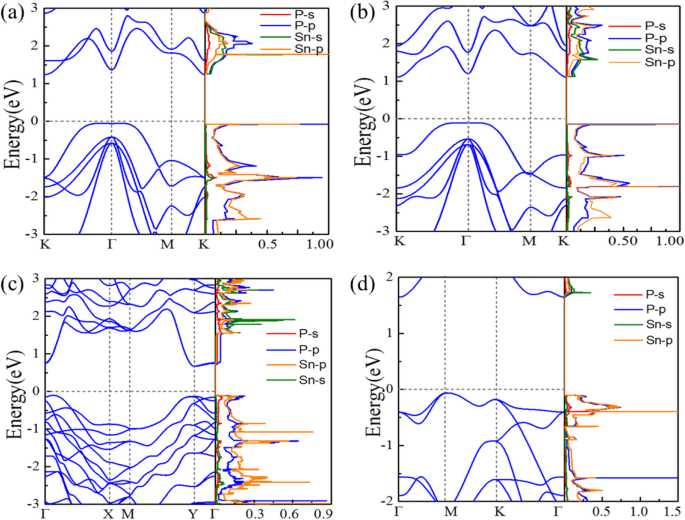
Structures de bandes électroniques calculées et densité partielle d'états du VBM et du CBM de Sn_x P_y monocouches :a P\( \overline{6} \)m2-SnP, b P\( \overline{3} \)m1-SnP, c Pmc2₁ -SnP₂ , et d P\( \overline{4}{2}_1 \)m-SnP₂

Selon le critère de Stoner, le ferromagnétisme spontané se produit si l'énergie cinétique est inférieure à l'énergie de séparation d'échange, c'est-à-dire si le DOS à E _F est assez élevé. La figure 2d montre le DOS très élevé autour du VBM; le P\( \overline{4}{2}_1 \)m-SnP₂ peut satisfaire le critère de Stoner si son E _F est déplacé vers une position avec un dopage de trou traversant DOS élevé. Comme le montre la figure 3a, le dopage des trous peut introduire des moments magnétiques à des concentrations de dopage appropriées. Comme prévu, le résultat du calcul suggère que le P\( \overline{4}{2}_1 \)m-SnP₂ peut être converti en un état fondamental ferromagnétique au-delà de la densité de trous critique. Parmi eux, la densité de trous n _h peut être exprimé par n _h =m _h /S _cellule , où S _cellule et m _h sont l'aire de la cellule primitive et le nombre de trous introduits dans la cellule primitive. L'injection du trou dans la monocouche P\( \overline{4}{2}_1 \)m-SnP₂ conduit en effet au ferromagnétisme. Le moment magnétique présente une relation de type pic abrupt avec la densité de trous. Parce qu'un moment de spin appréciable est induit par le dopage des trous dans le système, la structure de la bande d'énergie autour du niveau de Fermi a considérablement changé en raison de la division du spin. En particulier, la structure de bande polarisée en spin (montrée sur la figure 3b) de P\( \overline{4}{2}_1 \)m-SnP₂ à 7,2 × 10 ¹⁴ cm ⁻² montre que la monocouche devient un demi-métal parfait. Ainsi, nous prédisons que l'état FM stable avec une demi-métlicité peut être réalisé dans le P\( \overline{4}{2}_1 \)m-SnP₂ monocouche.

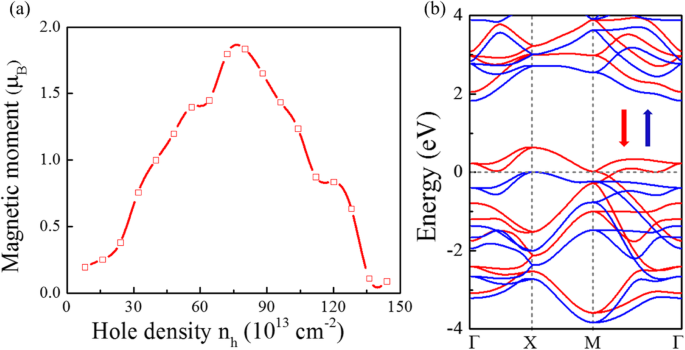
Ferromagnétisme dans P\( \overline{4}{2}_1 \)m-SnP₂ monocouche. (un ) Moments de rotation vs densité de trous n _h . b Structure de bande de valence calculée de P\( \overline{4}{2}_1 \)m-SnP₂ à n _h =7,2 × 10 ¹⁴ cm ⁻² . Les bandes de montée et de descente sont affichées respectivement en bleu et en rouge. Le niveau de Fermi est réglé à 0 eV

Anisotropie élastique et mobilité des porteurs de la monocouche

Les effets de déformation sur les propriétés électroniques des monocouches 2D Sn_x P_y les structures sont également intéressantes. La figure 4a présente la variation de la bande interdite sous déformation biaxiale ε . L'écart énergétique de Sn_x P_y monocouches est fortement modulée selon certaines règles. Par exemple, l'écart énergétique de P\( \overline{6} \)m2-SnP diminue de 1,19 à 0,52 eV avec l'augmentation de la déformation en traction jusqu'à ε =8 %, passant d'abord de 1,12 à 1,36 eV pour ε 2%, puis décroissant de 1,36 à 0,51 eV. De plus, depuis le a et b du paramètre de maille du Pmc2₁ -SnP₂ structure sont différentes, les changements de propriétés électroniques sont différents le long du x -axe et y -axe [48], comme le montre la figure 4b. Il est évident que lorsqu'une déformation uniaxiale est appliquée dans différentes directions, le changement de x la direction est différente du changement de y direction. Considérant la gamme des écarts énergétiques avec la déformation ε , la plage de bande interdite réglable par déformation dans le plan couvre presque toute la région de la lumière visible sur la base du calcul des premiers principes.

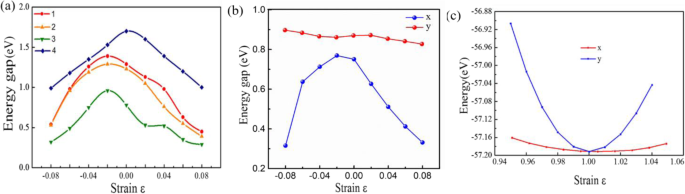
Propriétés électroniques des structures dépendantes de la contrainte :(1) P\( \overline{6} \)m2-SnP, (2) P\( \overline{3} \)m1-SnP, (3) Pmc2₁ -SnP₂ , et (4) P\( \overline{4}{2}_1 \)m-SnP₂ . b Propriétés électroniques dépendantes de la déformation uniaxiale de Pmc2₁ -SnP₂ . c Énergie du Pmc2₁ -SnP₂ monocouche vs coloration uniaxiale

En outre, nous avons également étudié l'effet de la contrainte uniaxiale, comme le montre la figure 4c. La rigidité dans le plan C ^2D (C ^2D =[∂ ² E /∂δ ² ]/S ₀ , où S ₀ est l'aire de 2D Pmc2₁ -SnP₂ monocouche) peut être obtenu en ajustant la parabole. Chose intéressante, la rigidité dans le plan C ^2D montrant une anisotropie élastique extrêmement évidente le long de a et b les directions sont calculées à 12,1 et 105,6 N/m, respectivement. Parce que le Pmc2₁ -SnP₂ présente un caractère semi-conducteur de type gap direct, les masses effectives (m ^∗ =ℏ ² (∂ ² E /∂K ² ) ⁻¹ ) d'électrons (m _e est |m ^* _e |) et des trous (m _h est |m ^* _h |) associé au semi-conducteur (quasi) direct Pmc2₁ -SnP₂ monocouche sont également calculés. Les masses effectives sont répertoriées (tableau 2). Le plus intéressant est la masse effective des électrons dans le k _b direction (0.15 me) est beaucoup plus petite que celle dans le k _un direction (1.31 me), indiquant la dérive facile des électrons dans le k _b direction. Il y a un autre paramètre important est la constante DP E ₁ (E ₁ =dE _bord /dδ ) pour les électrons le long de a et b directions est calculée pour être 5,36 et 11,57 eV, respectivement. Étonnamment, le transporteur calculé peut être atteint ~ 800 cm ² V ⁻¹ s ⁻¹ dans le k _b direction. A titre de comparaison, la mobilité des porteurs du MoS₂ monocouche est ∼ 200 cm ² V ⁻¹ s ⁻¹ dans les expériences [8]. Cependant, la mobilité du porteur est d'environ ∼ 8 cm ² V ⁻¹ s ⁻¹ dans le k _un direction. Par conséquent, la mobilité élevée des porteurs trouvée dans cette étude est d'une grande importance pour l'étude du transport des électrons.

Propriété optique

Les propriétés photoélectriques des matériaux photoélectroniques sont caractérisées par la fonction diélectrique, la photoconductivité et le coefficient d'absorption. Les parties imaginaires de la fonction diélectrique sont représentées sur la figure 5a. Notez que Pmc2₁ -SnP₂ monocouche montre une absorption commençant à 0,70 eV, et il apparaît trois pics d'absorption principaux à ∼ 0,9, ~ 3,2 et 4,0 eV. Comme illustré sur la figure 5b, il montre l'absorbance dans les trois directions dans le domaine visible et le domaine ultraviolet pour la monocouche Pmc2₁ -SnP₂ . Alors, Pmc2₁ -SnP₂ des matériaux monocouches pourraient être utilisés pour des photodétecteurs aveugles à l'état atomique pour, par exemple, une détection efficace des flammes.

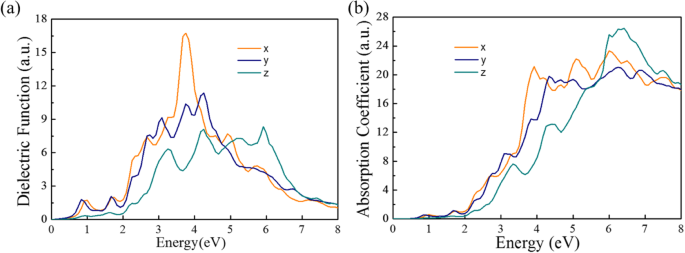
un Fonctions diélectriques calculées en fonction de l'énergie pour Pmc2₁ -SnP₂ suivant différentes directions de la lumière incidente. b Coefficient d'absorption imaginaire calculé

Conclusions

En conclusion, sur la base des algorithmes PSO combinés à des calculs de premiers principes, nous avons identifié plusieurs Sn_x 2D P_y monocouches avec les rapports de x /y =1:1 et 1:2. Étonnamment, ces nouvelles monocouches possèdent également des propriétés électroniques et magnétiques particulières :la monocouche de P\( \overline{4}{2}_1 \)m-SnP₂ structure à bande de valence unique structure pouvant passer de non magnétique à ferromagnétique par le dopage des trous en raison du « critère de Stoner »; le Pmc2₁ -SnP₂ la structure est un semi-conducteur à fente de type direct avec une anisotropie élastique dans le plan qui possède une mobilité électronique élevée pouvant atteindre 800 cm ² V ⁻¹ s ⁻¹ le long du k _b direction, qui est beaucoup plus élevée que celle de MoS₂ (∼ 200 cm ² V ⁻¹ s ⁻¹ ). Le pic d'absorption optique du matériau se situe dans le domaine ultraviolet. Ces découvertes élargissent les applications potentielles du domaine émergent du Sn_x 2D P_y structures en nanoélectronique. Ces propriétés souhaitables du multifonctionnel Sn_x P_y les monocouches offrent d'excellentes applications prometteuses en électronique et en optoélectronique.

Disponibilité des données et des matériaux

Ils sont tous dans le texte principal et les figures.