Propriétés électriques des matériaux composites avec alignement assisté par champ électrique des charges de nanocarbone

Contexte

Les propriétés personnalisables permettent une application des matériaux composites conducteurs à base de carbone dans de nombreuses industries en tant que composants électroniques et de construction :en microélectronique, dissipation électrostatique, à la fabrication de boucliers électromagnétiques, pour les structures aéronautiques, etc. [1,2,3,4]. Ils ne se corrodent pas comme les métaux, mais possèdent une résistance, un poids et une large gamme de valeurs de conductivité appropriés grâce à une variété de charges utilisées.

Les particules non sphériques sont plus favorables comme charges composites du point de vue de l'amélioration de la conductivité électrique du composite [5,6,7]. Cela est dû aux valeurs plus faibles du facteur de compactage lors de l'augmentation du rapport d'aspect des particules [8], qui est un paramètre du modèle de percolation statistique. Par conséquent, le développement de composites avec des nanotubes de carbone (CNT) et des nanoplaquettes de graphite (GNP), qui se caractérisent par des valeurs élevées de rapport d'aspect (10 ¹ –10 ⁴ ) [9], en tant que charges, est une direction très prometteuse. Outre l'anisotropie géométrique, les NTC et les PNB se distinguent par l'anisotropie des propriétés physiques. Mais lors de la distribution aléatoire de la charge au composite, l'anisotropie de la particule de charge individuelle est compensée. Par ailleurs, à répartition aléatoire des charges, une grande partie de celle-ci se concentre dans les branches dites « vierges » d'un réseau conducteur qui sont disjointes du réseau global. Ces pertes sont particulièrement importantes à faible teneur en charge dans le composite.

La recomposition de la charge et sa répartition spatiale spécifique permet d'obtenir des composites à faible seuil de percolation ce qui réduit le coût de la matière. Les méthodes les plus populaires de préparation de composites avec une distribution de charge anisotrope sont l'exposition du mélange composite liquide à un champ électromagnétique et l'application de contraintes mécaniques. Parmi les inconvénients de la méthode d'alignement des charges par laminage, la contrainte de cisaillement est la rupture et la destruction possibles des nanoparticules de carbone sous une telle exposition [10]. L'alignement induit par le champ magnétique nécessite l'ajout de composants magnétiques au composite [11]. Ainsi, l'alignement assisté par champ électrique de la charge dans le composite est la méthode la plus prometteuse de formation de composite anisotrope du point de vue de nombreux groupes de recherche [12, 13].

Mais l'écrasante majorité des travaux présentés sur l'alignement assisté par champ électrique sont consacrés aux nanotubes de carbone noyés dans une matrice polymère [14,15,16,17,18]. L'effet de la morphologie des particules de charge sur le processus d'alignement est très peu développé dans les études tant théoriques qu'expérimentales [19,20,21]. Le but de cette étude était d'étudier l'influence de la morphologie de la charge sur le processus de formation de composites alignés et d'identifier et d'expliquer les différences de dépendance à la concentration de la conductivité électrique des composites avec une distribution GNP aléatoire et alignée.

Méthodes

Matériaux

Sur la base de la résine époxy Larit 285 (Lange Ritter GmbH, Allemagne), des matériaux composites ont été fabriqués et étudiés dans cette étude. A l'état initial, ce polymère est à deux composants et se compose d'époxy liquide et d'un durcisseur approprié H 285. Faible viscosité de la résine utilisée (600 ÷ 900 mPa × s à 25 °С) et du durcisseur (50 100 mPa × s à 25 °С) permet d'utiliser l'impact d'un champ électrique externe pour la fabrication de matériaux composites à leur base.

Les matériaux suivants ont été utilisés comme charges pour les systèmes composites fabriqués :

• Nanotubes de carbone multiparois (MWCNT) (Cheap Tubes Ins, États-Unis) ;

• Nanoplaquettes de graphite (PNB).

Les PNB ont été obtenus par dispersion par ultrasons (dans un milieu acétonique pendant 3 h) de graphite exfolié thermiquement qui est un produit résultant d'un traitement thermochimique en profondeur du graphite dispersé. Le processus de fabrication du PNB est décrit en détail dans [22].

Le tableau 1 contient les paramètres des charges utilisées. Leurs dimensions et leur forme ont été estimées en utilisant l'AFM, le SEM et la microscopie optique dans les articles de notre groupe de recherche [23, 24]. Les particules GNP et MWCNT se distinguent par leur forme, leur taille et, par conséquent, leur rapport hauteur/largeur. Le tableau 1 contient les paramètres caractéristiques des particules les plus grosses, les plus petites et moyennes. Les particules sont marquées « max », « min » et « aver » par les valeurs de leur rapport hauteur/largeur. L'évaluation de la masse des particules a suggéré que la densité ρ (MWCNT) =1,8 g/cm ³ [25], ρ (PNB) =2,23 g/cm ³ , comme la densité du graphite monocristallin.

Fabrication composite

Les échantillons composites qui ont été préparés contenaient différentes concentrations de PNB en tant que charge (0,05, 0,5, 0,7, 1, 2, 3, 4, 5 % en poids). Un type d'échantillons avait une distribution aléatoire de la charge, et dans un autre, les PNB étaient alignés par un champ électrique externe.

La méthode de préparation des systèmes composites était la suivante. Au début, la quantité requise de charge de carbone a été versée dans une matrice polymère pré-dissoute et mélangée mécaniquement. Après cela, le mélange a été exposé à une dispersion par ultrasons pour une meilleure répartition de la charge dans la matrice époxy. La dispersion a été effectuée dans un bain à ultrasons Вaku-9050 avec une fréquence de 40 kHz et une puissance électrique de sortie maximale de 50 W. Le mélange composite a été exposé à une action ultrasonore pendant 30 min à 50 W, après que ce durcisseur Н 285 a été ajouté au composite résultant mélange en rapport 100/40 en masse au poids de Larit 285.

Finalement, pour les composites avec une fabrication de distribution de charge alignée, une partie du mélange composite obtenu a été versée dans un moule en plastique qui a été placé entre les plaques du condensateur. Une tension alternative avec une fréquence de 15 kHz et une amplitude de 2000 V a été appliquée aux plaques. Une source haute tension capable de générer une tension alternative à une fréquence de 15 kHz et une amplitude allant jusqu'à 2000 V ou une tension continue d'une amplitude allant jusqu'à 2000 V a été utilisée comme source de champ électrique. La valeur de l'amplitude du champ électrique a été contrôlée par le voltmètre universel В7-16А.

Lors du choix de la fréquence du champ électrique alternatif, nous avons gardé à l'esprit deux points :(1) la fréquence doit être suffisamment élevée pour que le temps d'alignement des nanoparticules de carbone soit le temps de durcissement de l'époxyde ; (2) la fréquence doit être suffisamment basse pour observer la dynamique de l'alignement des nanoparticules dans le champ électrique. En gardant à l'esprit ces considérations, nous avons réalisé la formation de composites à la fréquence de 15 kHz.

L'autre partie du mélange composite a été laissée sans l'influence d'un champ électrique externe.

Après avoir été maintenus à température ambiante, les moules avec des échantillons composites ont été soumis à un traitement thermique à une température augmentant progressivement de 40 à 80 °C, qui a augmenté de 10 °C toutes les heures. Cela a été fait pour terminer le processus de polymérisation des composites.

Microscopie optique

L'étude du caractère de la distribution des charges de carbone dans la matrice époxy sous traitement par champ électrique a été réalisée pour des composites avec une teneur en charge de carbone de 0,05 % en poids. Cela a été fait avec un microscope optique stéréoscopique МBS-1 équipé d'un appareil photo numérique Etrek DCM-510. Ce montage a permis d'observer en ligne l'époxyde liquide avec des nanoparticules de carbone dispersées sous influence de champ électrique. La configuration de l'expérience est décrite en détail dans [26, 27]. Une série d'observations optiques des composites MWCNTs/− et GNPs/Larit 285 a été menée en temps réel en alimentant des électrodes avec une tension alternative de 15 kHz ou une tension continue et en modifiant la valeur de l'amplitude du champ électrique.

Mesure des propriétés électriques

La conductivité électrique des composites étudiés a été mesurée par la méthode standard à deux sondes en mode CC à température ambiante avec une limite de mesure de résistance électrique de 10 ¹⁰ ohm. Supérieur à 10 ¹⁰ ohm, les résistances ont été mesurées à l'aide de teraommetr Е6–13. Des échantillons pour les mesures ont été préparés sous la forme de parallélépipèdes réguliers avec les dimensions 5,0 × 4,0 × 4,0 mm ³ .

Modélisation

Les équations permettant d'estimer le temps caractéristique de rotation des particules de carbone sous l'action d'un champ électrique ont été résolues à l'aide d'un logiciel mathématique Maple 13.

Résultats et discussion

Observations optiques

Les figures suivantes montrent des photos optiques de la surface des matériaux composites GNPs/Larit 285 (Figs. 1 et 2) et MWCNTs/Larit 285 (Figs. 3 et 4) [26] à faible teneur en charges (0,05 % en poids) à l'action du champ électrique AC.

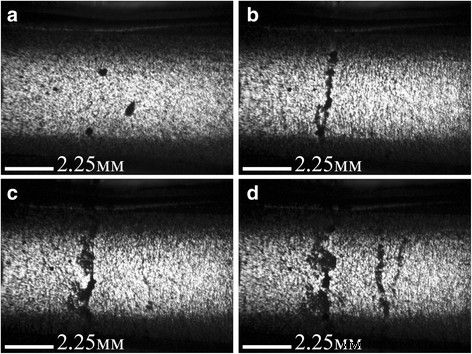
Images optiques de la formation de « claquage » électrique dans un composite PNB à 0,05 % en poids/Larit 285 sous l'action d'un champ électrique alternatif d'une intensité de 36 kV/m, fréquence de 15 kHz (électrodes intégrées) :a —avant l'action du champ électrique ; b — après 100 s; c — après 140 s; d —après 160 s d'action de champ électrique. Taille de l'image 10,8 × 8,0 mm ²

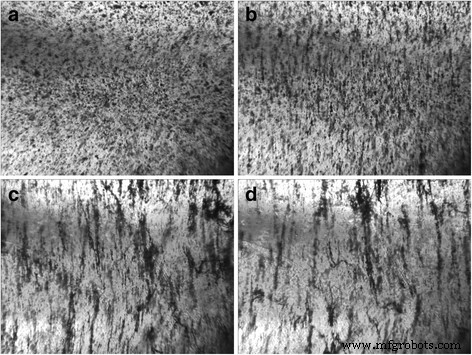
Images optiques de 0,05 % en poids de composite PNB/Larit 285 sous l'action d'un champ électrique alternatif (fréquence de 15 kHz, intensité de 167 kV/m) (en condensateur) :а— avant l'action du champ électrique ; b —après 12 minutes ; c — après 26 minutes; d —après 60 min d'action de champ électrique. Taille de l'image 10,8 × 8,0 mm ²

Images optiques de 0,05 % en poids de composite MWCNTs/Larit 285 sous l'action d'un champ électrique alternatif (fréquence de 15 kHz, intensité de 83,3 kV/m) (électrodes intégrées) :a – avant l'action du champ électrique ; b – après 12 min; c – après 26 min; d – après 60 min d'action de champ électrique. Taille de l'image 10,8 × 8,0 mm ² [26]

Images optiques de 0,05 % en poids de composite MWCNTs/Larit 285 sous l'action d'un champ électrique alternatif (fréquence de 15 kHz, force de 50 kV/m) (électrodes intégrées) :а —avant l'action du champ électrique ; b —après 12 minutes ; c — après 26 minutes; d —après 60 min d'action de champ électrique. Taille de l'image 10,8 × 8,0 mm ² [26]

Traités avec un champ électrique alternatif, les composites sont devenus plus transparents avec l'augmentation du temps d'action du champ électrique en raison du mouvement de la charge dans la direction des lignes électriques d'un champ électrique externe. Il a également été observé qu'avec l'augmentation du temps d'action du champ électrique, les structures alignées de la charge de carbone s'élargissent et des jeux apparaissent entre elles. Cela peut être dû aux interactions de Van der Waals avec les nanoparticules de carbone. De cette manière, des chaînes de charge nanocarbone de distribution spécifiée se forment dans le composite.

Comme le montre la figure 1, pour les composites GNP/Larit 285 dans une configuration d'électrodes intégrées, l'action du champ électrique alternatif se manifeste par la création du chemin conducteur principal, qui ferme l'alimentation avec des électrodes de tension externes et conduit à un flux de courant de haute amplitude à travers le échantillon composite. Par conséquent, l'alignement des PNB dans le Larit 285 a été effectué par l'ensemble expérimental lorsque le composite est placé entre des plaques de condensateur. La figure 2 montre qu'une telle configuration de configuration expérimentale dans laquelle le flux de courant à travers l'échantillon est impossible permet d'obtenir des chaînes de PNB alignées de manière cohérente dans la matrice polymère.

Dans le cas du traitement des composites MWCNTs/Larit 285 avec un champ électrique alternatif, une formation d'allongement dans la direction des chaînes de champ électrique a également été observée. Les chaînes distinctes deviennent plus épaisses lorsque le temps d'exposition au champ CA augmente. Mais le temps caractéristique de formation de chaînes alignées dans les composites MWCNTs/époxy est de quelques minutes tandis que dans les composites GNPs/époxy est de quelques secondes dans la configuration des électrodes intégrées. De plus, en raison de la forme et de la taille du GNP, une distribution de remplissage alignée dans les composites GNP/époxy peut être formée à des amplitudes de champ électrique alternatif inférieures à celles des composites MWCNT/époxy. Mais d'autre part, en raison de la mobilité des GNP en raison de sa forme et de sa taille par rapport aux MWCNT, la formation de composites en vrac avec une charge GNP est compliquée. Le réseau aligné de PNB a tendance à se détruire peu de temps après la coupure du champ électrique si le composite n'a pas complètement polymérisé.

Lorsque l'on considère toutes les images optiques du réseau aligné sous la formation de champ électrique AC dans les composites GNP/− et MWCNTs/époxy, nous pouvons conclure que dans des conditions égales en changeant uniquement le type de charge de carbone, le réseau aligné se forme plus rapidement dans les GNP/époxy composite. Dans le cas des MWCNT, leur tendance à l'agglomération empêche un alignement efficace dans la direction du champ électrique appliqué. Il convient de noter que le champ DC n'est pas efficace pour la formation d'un réseau aligné en composite [26].

Pour expliquer l'observation par microscopie optique des particularités de l'alignement assisté par champ électrique de la charge de morphologie différente, un temps caractéristique de rotation des nanoparticules de carbone dans une matrice époxy sous l'action d'un champ électrique alternatif a été théoriquement estimé.

Modélisation de l'alignement des particules de carbone en milieu visqueux

Le mécanisme du composite avec une distribution spatiale spécifiée de la méthode de formation de la charge est que chaque nanoparticule de carbone qui est incorporée dans la matrice diélectrique subit une polarisation sous l'action du champ électrique alternatif en raison de la polarisation de l'interface entre le polymère et la particule. Généralement, le moment de polarisation et le vecteur champ électrique sont non colinéaires en raison de l'anisotropie des nanoparticules. Par conséquent, lorsque le champ électrique est activé, un couple qui conduit à la rotation des nanoparticules de carbone dans le sens du champ se produit. On sait que le mouvement de rotation d'une particule dans ce cas est décrit par l'équation suivante [16] :

où je est le moment d'inertie de la nanoparticule de carbone; Θ est l'angle entre la particule et la direction du champ électrique ; T _η est un couple d'amortissement; \( {T}_{\mathrm{align}}\approx \left[\overrightarrow{\mu}\times \overrightarrow{E}\right] \) est un couple induit par le champ ; \( \overrightarrow{\mu}=f\left(\varepsilon, {\sigma}_1,{\sigma}_2,v\right) \) est le moment de polarisation qui dépend des valeurs de constante diélectrique ( ) et la conductivité (σ ₁ , σ ₂ ) de nanoparticule et de matrice ; v = f (m , l , d ) est le volume de nanoparticule de carbone qui dépend de son poids (m ) et dimensions (l , d ).

Généralement, le moment de polarisation \( \overrightarrow{\mu} \) est proportionnel au champ externe \( \overrightarrow{E} \) et au volume de la particule ν et est déterminé par la formule [28] :

où ε ₀ est la permittivité de l'espace libre, ε _m est une constante diélectrique de la matrice, β est un paramètre sans dimension qui dépend notamment de la forme de l'inclusion. Dans [28], les formules de β pour un disque et un cylindre conducteurs idéaux sont donnés :

Il découle de ces dépendances que \( {\overrightarrow{\mu}}_{II}\ne {\overrightarrow{\mu}}_{\perp } \) (II signifie codirection du grand axe de la particule et de la direction du champ, -perpendicularité). Ainsi, pour les PNB et les MWCNT, \( {\overrightarrow{\mu}}_{II}>{\overrightarrow{\mu}}_{\perp } \) en raison de leur forme et de leurs propriétés.

Pour évaluer le temps caractéristique de rotation des particules de carbone sous l'action d'un champ électrique et son alignement par la direction du champ Eq. (1) avec les conditions initiales Θ (t = 0) = Θ ₀ , \( \frac{d\varTheta }{dt}\left(t=0\right)=0 \) ont été résolus. Selon [16], les termes de l'équation principale du mouvement sont les suivants :

où \( {\alpha}^{\ast }=\left({\left({\varepsilon}_p^{\ast }-{\varepsilon}_m^{\ast}\right)}^2\right) /\left(\left[{\varepsilon}_m^{\ast }+\left({\varepsilon}_p^{\ast }-{\varepsilon}_m^{\ast}\right){L}_x\ right]\left({\varepsilon}_p^{\ast }+{\varepsilon}_m^{\ast}\right)\right) \) est une polarisabilité, \( {\varepsilon}_{m,p} ^{\ast }={\varepsilon}_{m,p}-j\frac{\sigma_{m,p}}{\omega } \), et ε _{m , p} , σ _{m , p} sont la constante diélectrique et la conductivité du milieu et de la particule, ω = 2πf , f —fréquence du champ électrique.

Pour déterminer le facteur de dépolarisation des nanotubes de carbone et des nanoplaquettes de graphite, ils doivent être considérés comme des particules d'une certaine forme (Fig. 5). MWCNT peut être considéré comme ellipsoïde uniquement. L'ellipticité du MWCNT dans l'approximation ellipsoïde est \( e=\sqrt{1-{\left(2{r}_0/l\right)}^2} \). Le PNB peut être considéré comme sphéroïde ou comme ellipsoïde. L'ellipticité du PNB en approximation ellipsoïde est \( e=\sqrt{1-{\left(h/2R\right)}^2} \) et en approximation sphéroïde est \( e=\left(2R/h\ right)\sqrt{1-{\left(h/2R\right)}^2} \). Alors les expressions du facteur de dépolarisation prennent la forme suivante [28].

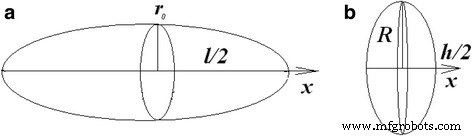
Images schématiques de nanotubes de carbone (a ) et des nanoplaquettes de graphite (b )

Pour l'ellipsoïde :

Pour le sphéroïde :

Dans les équations ci-dessus, L _x est un facteur de dépolarisation si le champ externe est appliqué le long du x -axe (comme dans la Fig. 5), L _R est un facteur de dépolarisation si le champ externe est appliqué le long du rayon du PNB.

En dépensant les facteurs de dépolarisation en série, les expressions ci-dessus prennent la forme suivante.

Pour le MWCNT ellipsoïdal :

Pour le PNB ellipsoïdal :

Pour le PNB sphérique :

De plus, pour mettre en évidence les particularités de la morphologie des particules, le volume CNT a été demandé comme le volume d'un cylindre creux \( \nu =\pi l\left({r}_0^2-{r}_i^2\right)\ ), tandis que le volume PNB a été demandé comme le volume d'un disque ν = πR ² h .

Le moment d'inertie des nanotubes de carbone a été pris comme \( I=\frac{ml^2}{12} \)—le moment d'inertie d'une tige mince et droite de longueur l et masse de m , l'axe de rotation est perpendiculaire à la tige et passe par son centre de masse. Le moment d'inertie des nanoplaquettes de graphite a été pris comme \( I=\frac{mR^2}{2} \)—le moment d'inertie du disque, dont le rayon est R , et masse de m , le disque tourne autour de la perpendiculaire à son axe plan.

Ensuite, en utilisant toute l'approche précédente et en définissant des paramètres numériques, des calculs du changement d'angle d'inclinaison des particules de morphologie différente par rapport à la direction du champ avec le temps de traitement du champ électrique alternatif ont été effectués.

En se basant sur le papier [29] où les dépendances expérimentales de la concentration des parties réelles et complexes de la permittivité diélectrique des composites avec du graphite fin et des nanotubes de carbone ont été décrites par la formule et les équations de Nielsen.

sont donnés, dans nos calculs pour le PNB ε _{p (PNB )} =34.3, et pour MWCNT, ε _{p (CNT )} =62,2 a été pris.

Les paramètres géométriques des particules ont été extraits du tableau 1. Concernant les autres paramètres numériques utilisés, il a été mis que ε ₀ =8.85 × 10 ⁻¹² F/m, η =0,75 Pa × s, f =15 kHz, ε _m =2.8ε ₀ [30], σ _m =10 ⁻⁶ Sm/m [16]. La conductivité des particules de carbone individuelles a été prise comme σ _{p (CNT )} =10 ⁵ Sm/m [31], σ _{p (PNB )} =10 ⁵ Sm/m [32, 33]_.

La figure 6 montre l'angle d'inclinaison de la particule par rapport à la direction de la dépendance du champ appliqué au temps d'action du champ lorsque L _x a été évalué par les équations. (2) et (3). Les résultats ont été trouvés pour deux valeurs d'intensité de champ :1 kV/m (Fig. 6а) et 36 kV/m (Fig. 6b) en supposant que la particule est presque complètement désordonnée à l'instant initial (Θ (t = 0) = π /2.05).

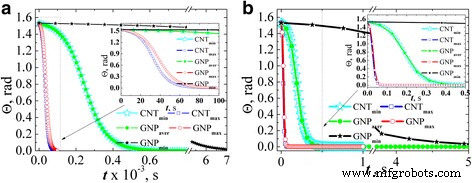
L'évolution de l'angle d'inclinaison des particules de charge de carbone par rapport à la direction du champ estimée dans l'approximation des ellipsoïdes pour l'intensité du champ électrique AC 1 kV/m (a ) et 36 kV/m (b )

Il y a eu une corrélation claire entre le rapport d'aspect des particules et le temps d'alignement par le champ électrique. A savoir, le temps maximum pour l'alignement est pour les particules avec le rapport d'aspect le plus bas (PNB_min ). Pour le PNB_max et CNT_max , le temps d'alignement est presque égal, et le même temps d'alignement est pour le PNB_aver et CNT_min .

La figure 7 montre les valeurs des facteurs de dépolarisation qui ont été estimées par les équations. (2) et (3) pour les PNB et les MWCNT. L _x est un facteur géométrique et ne dépend pas des valeurs absolues des demi-axes des ellipsoïdes simulés mais de leur rapport. Ainsi, L _x est une fonction directe du rapport hauteur/largeur des particules.

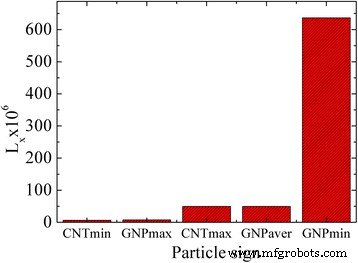
Facteur de dépolarisation pour les PNB et les MWCNT évalués par les équations. (2) et (3)

C'est-à-dire que le facteur de dépolarisation est le paramètre principal du problème. Étant donné que son expression dépend de la morphologie et de la taille des particules, un temps caractéristique de rotation des PNB et des MWCNT diffère.

Contenu de la figure 8 analogue à celui de la figure 6 dépendances de l'angle d'inclinaison des PNB par rapport à la direction du champ appliqué sur le temps d'action du champ lorsque L _R a été évalué par l'Eq. (5). Les résultats ont été trouvés pour deux valeurs d'intensité de champ :1 kV/m (Fig. 8а) et 36 kV/m (Fig. 8b) en supposant que les particules sont presque complètement désordonnées à l'instant initial (Θ (t = 0) = π /2.05). A titre de comparaison, les résultats des calculs de la dépendance angulaire pour les MWCNT (L _x a été évalué par l'Eq. (2)) sont introduits dans les mêmes graphiques.

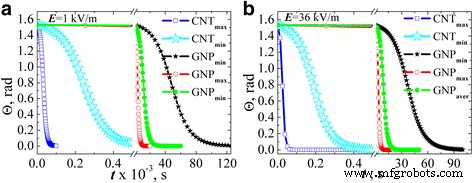
L'évolution de l'angle d'inclinaison des particules de charge de carbone par rapport à la direction du champ estimée en approximation ellipsoïdes pour les MWCNT et en approximation sphéroïde pour les PNB à une intensité de champ électrique AC 1 kV/m (a ) et 36 kV/m (b )

La figure 9 montre les dépendances de l'angle d'inclinaison des PNB par rapport à la direction du champ appliqué sur le temps d'action du champ dans l'approximation que le PNB est un sphéroïde avec un facteur de dépolarisation (4). L'évaluation a été effectuée pour l'intensité du champ électrique AC 1 kV/m (Fig. 9а) et 36 kV/m (Fig. 9b) en supposant qu'au moment initial la particule est approximativement désordonnée (Θ (t = 0) = π /2.05).

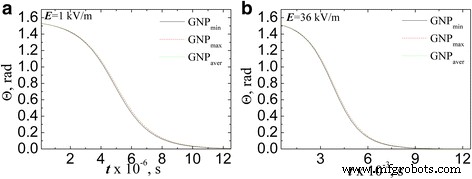
L'évolution de l'angle d'inclinaison des PNB par rapport à la direction du champ estimée en approximation sphéroïde (L _x a été prise par l'Eq. (4)) à une intensité de champ électrique AC 1 kV/m (a ) et 36 kV/m (b )

À partir de l'analyse présentée dans les données de la figure 9, les conclusions suivantes ont été tirées :tout d'abord, si nous supposons que l'axe du champ électrique est co-dirigé avec le x -axe du PNB, le temps de rotation augmente significativement par rapport au calcul dans le cas de la codirection axe de champ et rayon du PNB. Et ce comportement est indépendant du rapport hauteur/largeur du PNB. Deuxièmement, le cours de la dépendance est légèrement différent pour les particules avec des rapports d'aspect différents, et à un certain moment du processus, la particule la plus alignée est la particule avec un rapport d'aspect minimum GNP_min tandis que le PNB_moyen et PNB_max les angles coïncident. Ce comportement est dû à la valeur du facteur dépolarisant qui est proche de 1 pour les cas ci-dessus.

Ainsi, l'estimation a montré que le temps de rotation des particules de carbone sous l'action d'un champ électrique alternatif dépend de leur morphologie et de leur rapport d'aspect. Notez que le modèle considère une particule intégrée dans la matrice polymère alors que dans le composite, nous avons un ensemble de particules avec différents angles d'inclinaison initiaux. C'est l'une des raisons pour lesquelles le temps caractéristique réel de l'ensemble de la formation du réseau peut être très différent du temps estimé.

De plus, il est compliqué de réaliser une telle distribution de MWCNTs dans un mélange composite où chaque tube individuel est enchevêtré. Il est connu que les nanotubes de carbone ont tendance à s'emmêler en raison de l'interaction de leurs surfaces. Par conséquent, le temps réel des MWCNT dans l'alignement des mélanges composites est significativement plus élevé qu'il n'a été estimé théoriquement. En outre, la viscosité du mélange composite avec la même teneur en MWCNT est supérieure à la viscosité du mélange composite avec les PNB. Tous ces facteurs empêchent un alignement aussi rapide des MWCNT dans le composite tel qu'il a été estimé.

Propriétés électriques des composites solides

Dans le cadre de l'étude, des valeurs de résistivité des composites GNPs/Larit 285 préparés avec une distribution de charge alignée et aléatoire dans la matrice époxy ont été trouvées expérimentalement. La figure 10 présente les dépendances de concentration de la conductivité électrique des composites GNPs/Larit 285 avec une distribution de remplissage alignée et aléatoire. Les propriétés électriques des échantillons composites ont été étudiées dans le sens longitudinal et perpendiculaire à la direction du champ électrique appliqué à la fabrication du composite. La figure 11 présente les dépendances de concentration de la conductivité pour les composites MWCNTs/Larit 285 (а) [27] et PNB/Larit 285 (b) en échelle log-log.

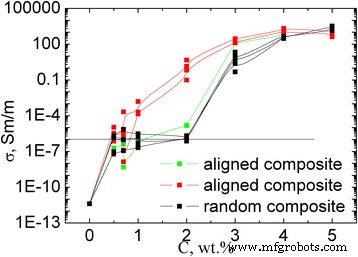
Dépendance de la concentration de la conductivité électrique des composites PNB/Larit 285 avec une distribution de remplissage alignée et aléatoire en échelle logarithmique

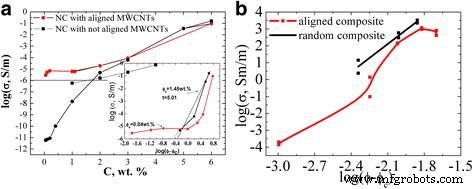
Dépendance à la concentration de la conductivité des MWCNTs/Larit 285 (а ) [27] et PNB/Larit 285 (b ) à l'échelle log-log

Les valeurs les plus basses de la conductivité σ correspondent aux échantillons de résine époxy sans charge (conductivité de 10 ⁻¹¹ Sm/m). Avec des PNB s'ajoutant au composite, sa conductivité augmente et atteint la valeur de σ =10 ⁻⁶ Sm/m (cette valeur est considérée comme le niveau de percolation) au contenu PNB с en composite de φ _с =2 wt% for the composites with random filler distribution. For the GNPs/Larit 285 composites with aligned filler distribution, percolation concentration is of φ _с =0.84 wt%. Thus, materials of the identical composition are characterized by different values of percolation threshold depending on the method of preparation and filler distribution in the polymer matrix (aligned or random).

Conductivity of GNPs/Larit 285 composites smoothly increases with the increment of GNPs content for both types of the samples while the shape of the dependence is completely different for the MWCNTs/Larit 285 composites obtained by the same method [27] (see Fig. 11). Concentration dependence of conductivity of MWCNTs/Larit 285 composites increases with the increment of MWCNTs content at low filler content until it reaches a plateau, then conductivity increases again. Such a difference of conductivity concentration dependence can be explained by another process of conductive network formation if the fillers are of different morphology. MWCNTs/epoxy composites are characterized by crossed framework structure formation while in GNPs/epoxy composites chained structure appears. GNPs addition to the polymer matrix smoothly increases the number of conductive links in composite. In case of entangled by themselves frame MWCNTs, there is an area where nanotubes addition to the matrix has little effect on its conductivity.

Statistical percolation model operates with probabilities of particles in composite to create a conductive chain at their certain content. As it was shown in our paper, manufactured with electric field treatment, composites become conductive at lower content of carbon filler due to activation of dynamic percolation which is a phenomenon when conductive chain formation is stimulated by external influences at such a content of conductive particles in composite which is not enough for statistical percolation.

It should be noted that the existence of two types of percolation transitions is a characteristic feature of composite materials which are in low-viscosity state during the manufacture [34]. The higher value of percolation concentration cannot be changed by varying the manufacturing conditions of the composite since it is defined by statistical percolation theory. Statistical percolation threshold is defined by the filler type, its aspect ratio, surface state of polymer and filler, wettability, uniformity of filler distribution, and its content in polymer matrix. As we have shown, dynamical percolation threshold can be shifted by activating of filler particle movement in polymer matrix, by electric field action, and, thus, promoting a conductive network formation. The value of dynamic percolation threshold can be changed with method of composite manufacture change. We have established that in case of filler alignment under electric field action, dynamical percolation threshold is defined not only by the above parameters but also by parameters of the applied field and polymer matrix viscosity, filler morphology.

Conclusions

1. 1.

   Nanocarbon-polymer composite material with aligned distribution of graphite nanoparticles in epoxy matrix has been produced by exposing to a high-voltage AC electric field. The influence of electric field treatment time, strength, and configuration of electric field on formation of aligned GNPs network in liquid polymer medium was investigated by optical microscopy.

2. 2.

   It was shown that the influence of AC electric field at composite fabrication process leads to the manifestation of two types of percolation transitions:statistical and dynamic ones. In addition, the aspect ratio of the filler particles and the character of the formation of the conducting cluster, depending on the shape of the particles, determine the shape of the σ =f(c) dependence and the critical concentration of both dynamic and statistical percolation thresholds.

3. 3.

   The effects of the morphology of the filler particles on the process of nanocarbon alignment in polymer matrix under AC electric field have been investigated by estimating of carbon nanotube and graphite nanoplatelet rotation time using an analytical model based on effective medium approach. The theoretical evaluation of characteristic time of carbon nanoparticle of different morphology rotation under AC electric field action have shown that rotation time of carbon nanoparticle is determined by its depolarization factor which in turn depends directly on the aspect ratio of particle.

4. 4.

   The investigation of concentration dependences of conductivity of composites GNPs/Larit 285 with aligned by AC electric field action filler distribution and random filler distribution in epoxy matrix have shown that under AC electric field action composites, percolation threshold decreases essentially from ϕ _c =2 wt% for composites with random filler distribution of GNPs to ϕ _c =0.84 wt% for the obtained under AC electric field action GNPs/Larit 285 composites.

Abréviations

AC:

Alternative current

AFM:

Microscopie à force atomique

CNTs:

Carbon nanotubes

DC:

Direct current

GNPs:

Graphite nanoplatelets

MWCNTs:

Multiwall carbon nanotubes

SEM :

Microscopie électronique à balayage