Une méthodologie en deux étapes pour étudier l'influence de l'agrégation/l'agglomération de nanoparticules sur le module d'Young des nanocomposites polymères

Résumé

Une technique en deux étapes basée sur des modèles micromécaniques est suggérée pour déterminer l'influence des nanoparticules agrégées/agglomérées sur le module de Young des nanocomposites polymères. Le nanocomposite est supposé inclure une agrégation/agglomération de nanoparticules et des phases matricielles efficaces. Cette méthode est examinée pour différents échantillons, et les effets de paramètres importants sur le module sont étudiés. De plus, les niveaux les plus élevés et les plus bas de module prédit sont calculés sur la base de la méthodologie actuelle. La technique suggérée peut prédire correctement le module de Young pour les échantillons en supposant l'agrégation/agglomération de nanoparticules. De plus, l'agrégation/agglomération de nanoparticules diminue le module de Young des nanocomposites polymères. Il est démontré que le module élevé des nanoparticules n'est pas suffisant pour obtenir un module élevé dans les nanocomposites, et la chimie de surface des composants doit être ajustée pour empêcher l'agrégation/l'agglomération et pour disperser les particules de taille nanométrique dans la matrice polymère.

Contexte

De nombreux chercheurs se sont concentrés sur les nanocomposites polymères ces dernières années afin de déterminer les paramètres efficaces dans les relations traitement-structure-propriétés et d'optimiser les performances globales telles que mesurées par les propriétés mécaniques, thermiques, physiques et barrières [1,2,3,4 ]. Une faible teneur en nanoparticules dans les nanocomposites polymères produit une grande surface interfaciale, un module élevé, un faible poids et des produits peu coûteux qui sont extrêmement attrayants dans l'industrie des composites. Par conséquent, l'application de nanoparticules est un moyen simple, efficace et économique d'améliorer les performances des matrices polymères. Les effets de nombreux paramètres de matériaux et de traitement sur les propriétés des nanocomposites polymères contenant des couches de silicate (nanargile), des nanotubes de carbone (CNT) et des charges inorganiques telles que la silice (SiO₂ ), et le carbonate de calcium (CaCO₃ ) ont fait l'objet d'une enquête [5,6,7,8].

La taille et la qualité de dispersion/distribution des nanoparticules dans la matrice polymère modifient les propriétés générales des nanocomposites polymères. Les nanoparticules ont tendance à s'agréger et à s'agglomérer, en raison de l'attraction entre les nanoparticules telles que les forces de van der Waals et les liaisons chimiques [9] ou la forte réduction de la séparation de surface lorsque la taille de la charge diminue [10]. Par conséquent, il est difficile de disperser les nanoparticules dans des matrices polymères à l'échelle nanométrique. L'agrégation et l'agglomération sont toutes deux des assemblages de nanoparticules, où l'agrégation comprend des colonies de particules fortes et denses, mais l'agglomération comprend des particules faiblement combinées qui peuvent être perturbées par des forces mécaniques. L'agglomération/l'agrégation est évidente à des teneurs élevées en charge, ce qui détériore l'échelle nanométrique de la charge et produit de nombreux défauts et concentrations de contraintes dans les nanocomposites [11,12,13]. L'agglomération/l'agrégation réduit également la zone interfaciale entre la matrice polymère et les nanoparticules, ce qui diminue l'implication mécanique des chaînes polymères dans les nanoparticules et élimine l'effet raidisseur. Nos découvertes récentes [14, 15] et l'étude de Ji et al. [16] sur les propriétés mécaniques ont indiqué que toute agrégation/agglomération endommage gravement l'effet raidisseur des nanoparticules dans les nanocomposites polymères.

En plus de la caractérisation expérimentale des nanocomposites, les investigations théoriques qui quantifient la dépendance du comportement mécanique sur les propriétés des phases constitutives et la morphologie géométrique des nanoparticules ont introduit des défis intéressants dans la recherche récente. Des études théoriques peuvent aider à élucider les résultats expérimentaux et faciliter la synthèse optimale de nanocomposites très prometteurs. Les nanoparticules dans les nanocomposites introduisent du désordre dans la matrice adjacente, conduisant à la formation de zones d'interphase entourant la charge, qui présentent des propriétés différentes de la matrice en vrac et des nanoparticules [17,18,19]. Des études théoriques sur les propriétés d'interphase ont montré des résultats intéressants, justifiant l'utilisation de nanoparticules dans des nanocomposites polymères [20,21,22].

Les effets de l'agrégation/agglomération sur les performances mécaniques des nanocomposites ont été étudiés dans des travaux antérieurs [11, 14, 23, 24]. Ces études ont généralement considéré l'agrégation/agglomération par de grosses particules. Récemment, des méthodes de modélisation multi-échelles ont été utilisées pour étudier les propriétés des nanocomposites [25,26,27]. Dans le présent article, une méthode en deux étapes est suggérée pour examiner le rôle de l'agrégation/agglomération de nanoparticules dans le module de Young des nanocomposites polymères en supposant la fraction de la phase d'agrégation/agglomération dans le nanocomposite et la partie des nanoparticules dans les agrégats/agglomérats. À cet égard, deux modèles micromécaniques de Paul et Maxwell sont appliqués pour exprimer le module de Young des nanocomposites. De nombreuses données expérimentales sont présentées pour évaluer les prédictions. De plus, les effets des paramètres d'agrégation/agglomération sur le module de Young des nanocomposites sont étudiés.

Méthodes

Lorsqu'une fraction de particules de taille nanométrique s'agrège/s'agglomère, une distribution non uniforme des nanoparticules est montrée dans le nanocomposite. En conséquence, certaines nanoparticules peuvent être supposées dans des régions sphériques de la matrice en tant que phase d'agrégation/agglomération et d'autres sont uniformément dispersées dans la matrice polymère, comme illustré sur la figure 1. En conséquence, la nanocharge présente deux parties avec un renforcement différent qui peut être ont considéré deux phases différentes dans le calcul en tant que phases d'agrégation/agglomération et de matrice efficace qui démontrent les régions à l'intérieur et à l'extérieur des sphères, respectivement (Figure 1).

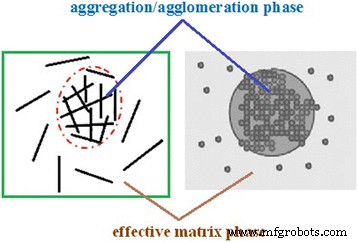
Illustration schématique de l'agrégation/agglomération et des phases matricielles efficaces dans des nanocomposites polymères contenant des nanoparticules en couches et sphériques

Les deux paramètres suivants sont suggérés pour le niveau d'agrégation/agglomération des nanoparticules dans un nanocomposite polymère :

$$ z=\frac{V_{\mathrm{agg}}}{V} $$ (1) $$ y=\frac{V_f^{\mathrm{agg}}}{V_f} $$ (2)

où « V _agg » et « V ” désignent respectivement les volumes totaux de phase d'agrégation/agglomération et de nanocomposite. Aussi, « V _f ^agg » et « V _f ” montrent les volumes de nanoparticules dans la phase d'agrégation/agglomération et le nanocomposite entier, respectivement. La fraction volumique de nanoparticules incorporées dans la phase d'agrégation/agglomération est présentée par :

$$ {\phi}_f^{\mathrm{agg}}=\frac{V_f^{\mathrm{agg}}}{V_{\mathrm{agg}}}=\frac{y{\phi}_f} {z} $$ (3)

où « ϕ _f ” est la fraction volumique de nanocharge dans les nanocomposites. Aussi, la fraction volumique de nanoparticules bien dispersées incorporées dans la phase de matrice efficace (hors phase d'agrégation/agglomération) est calculée par :

$$ {\phi}_f^{\mathrm{mat}}=\frac{V_f-{V}_f^{\mathrm{agg}}}{V-{V}_{\mathrm{agg}}}=\frac{\left(1-y\right){\phi}_f}{1-z} $$ (4)

Dans cette étude, une méthodologie en deux étapes basée sur les modèles micromécaniques est utilisée pour déterminer les paramètres d'agrégation/agglomération (z et y ) dans des nanocomposites polymères par le module de Young. Premièrement, le module d'agrégation/agglomération et les phases matricielles effectives sont calculés par le modèle de Paul. Deuxièmement, la phase d'agrégation/agglomération est supposée être des inclusions sphériques dans la matrice efficace, et le module de Young du nanocomposite est calculé par le modèle de Maxwell pour un composite contenant des particules dispersées.

Paul [28] a suggéré un modèle qui suppose la contrainte macroscopiquement homogène dans deux composants du composite comme :

$$ E={E}_{\mathrm{m}}\frac{1+\gauche(a-1\droit){\phi}_f^{2/3}}{1+\gauche(a-1 \right)\left({\phi}_f^{2/3}-{\phi}_f\right)} $$ (5) $$ a=\frac{E_{\mathrm{f}}}{E_ {\mathrm{m}}} $$ (6)

où « E _m " et " E _f ” sont respectivement les modules de Young des phases de matrice polymère et de charge. A la première étape, le module d'agrégation/agglomération (E _agg ) et matrice efficace (E _tapis ) les phases sont calculées par le modèle de Paul en remplaçant « ϕ _f ” avec “$ {\phi}_f^{agg} $” et “$ {\phi}_f^{mat} $” comme :

$$ {E}_{\mathrm{agg}}={E}_{\mathrm{m}}\frac{1+\left(a-1\right){\phi_f^{\mathrm{agg}} }^{2/3}}{1+\gauche(a-1\droit)\gauche({\phi_f^{\mathrm{agg}}}^{2/3}-{\phi}_f^{\ mathrm{agg}}\right)}={E}_{\mathrm{m}}\frac{1+\left(a-1\right){\left(\frac{y{\phi}_f}{ z}\right)}^{2/3}}{1+\left(a-1\right)\left[{\left(\frac{y{\phi}_f}{z}\right)}^ {2/3}-\frac{y{\phi}_f}{z}\right]} $$ (7) $$ {E}_{\mathrm{m}\mathrm{at}}={E} _{\mathrm{m}}\frac{1+\gauche(a-1\droit){\phi_f^{\mathrm{m}\mathrm{at}}}^{2/3}}{1+\ gauche(a-1\droit)\gauche({\phi_f^{\mathrm{m}\mathrm{at}}}^{2/3}-{\phi}_f^{\mathrm{m}\mathrm{ at}}\right)}={E}_{\mathrm{m}}\frac{1+\left(a-1\right){\left[\frac{\left(1-y\right){ \phi}_f}{1-z}\right]}^{2/3}}{1+\left(a-1\right)\left[{\left(\frac{\left(1-y\ droite){\phi}_f}{1-z}\right)}^{2/3}-{\left(\frac{\left(1-y\right){\phi}_f}{1-z }\droit)}^{2/3}\droit]} $$ (8)

De plus, le modèle de Maxwell [29] pour les composites contenant des charges dispersées est donné par :

$$ E={E}_{\mathrm{m}}\frac{1+2{\phi}_f\left(a-1\right)/\left(a+2\right)}{1-{ \phi}_f\gauche(a-1\droite)/\gauche(a+2\droite)} $$ (9)

A la deuxième étape, le modèle de Maxwell est appliqué pour le calcul du module dans un composite contenant une matrice efficace (matrice et nanoparticules bien dispersées) et des phases d'agrégation/agglomération en remplaçant "ϕ _f " avec "z » (voir Éq. 1), « E _f ” avec le module de phase d'agrégation/agglomération (E _agg ) et "E _m ” avec le module de matrice efficace (E _tapis ) comme :

$$ E={E}_{\mathrm{mat}}\frac{1+2z\left(k-1\right)/\left(k+2\right)}{1-z\left(k- 1\right)/\left(k+2\right)} $$ (10) $$ k={E}_{\mathrm{agg}}/{E}_{\mathrm{mat}} $$ ( 11)

qui corrèle le module de Young des nanocomposites aux modules des agrégats/agglomérats et de la matrice efficace ainsi que le paramètre « z ». Lorsque « E _agg " et " E _tapis ” à partir des éq. 7 et 8 sont entrés dans ces dernières équations, le module des nanocomposites est exprimé en utilisant la concentration de charge, le module de charge, le module de matrice et « z " et " y " paramètres. La dépendance du module sur ces paramètres est raisonnable, car les propriétés du polymère et des nanoparticules ainsi que l'étendue de l'agrégation/agglomération de la charge contrôlent le module des nanocomposites. Dans la méthodologie actuelle, y> z est significatif, car $ {VV}_f^{\mathrm{agg}}>{V}_f{V}_{\mathrm{agg}} $.

Résultats et discussion

La méthode proposée est appliquée pour évaluer l'agrégation/agglomération de nanoparticules dans plusieurs échantillons d'études précédentes, y compris PVC/CaCO₃ [30], PCL/nanoclay [31], ABS/nanoclay [32], PLA/nanoclay [33], PET/MWCNT [34] et polyimide/MWCNT [35]. La figure 2 montre les résultats expérimentaux du module de Young ainsi que les prédictions de la méthode en deux étapes. Les calculs suivent correctement les données expérimentales à différentes concentrations de nanocharge, illustrant l'exactitude de la méthode suggérée. Cependant, l'accord le plus élevé entre les données expérimentales et théoriques est obtenu lorsque l'agrégation/agglomération de nanoparticules est supposée par des niveaux appropriés de « z " et " y " paramètres. Les prédictions les plus élevées de "z " et " y ” les paramètres sont calculés comme z = 0.2 et y = 0.95 pour PVC/CaCO₃ nanocomposite. Aussi, (z , y ) des valeurs de (0,3, 0,75), (0,1, 0,99) et (0,35, 0,7) sont obtenues pour les échantillons PCL/nanoclay, PLA/nanoclay et PET/MWCNT, respectivement. De plus, (z , y ) des niveaux de (0,2, 0,93) et (0,15, 0,9) sont calculés pour les nanocomposites PET/MWCNT et polyimide/MWCNT, respectivement. Ces niveaux de « z " et " y » Les paramètres démontrent la formation de nanoparticules agrégées/agglomérées dans les nanocomposites mentionnés. La faible amélioration du module dans ces échantillons confirme la faible dispersion et le niveau élevé d'accumulation de nanoparticules dans les matrices polymères. Par exemple, l'ajout de 7,5 % en poids de CaCO₃ au PVC n'augmente que le module du PVC pur (1,13 GPa) à 1,3 GPa. De plus, l'incorporation de 10 % en poids de nanoargile dans le PCL n'améliore que le module du PCL pur de 0,22 à 0,37 GPa. Cependant, les nanoparticules présentent un module élevé par rapport aux matrices polymères. Module de Young du CaCO₃ , nanoargile et MWCNT ont été rapportés comme étant respectivement de 26, 180 et 1000 GPa [36], tandis que le module de Young des matrices polymères actuelles atteint à peine 2,5 GPa. En conséquence, les nanoparticules agrégées/agglomérées diminuent considérablement le module dans les nanocomposites, et la présente méthodologie suggère des données acceptables pour l'agrégation/l'agglomération de nanoparticules dans les nanocomposites polymères.

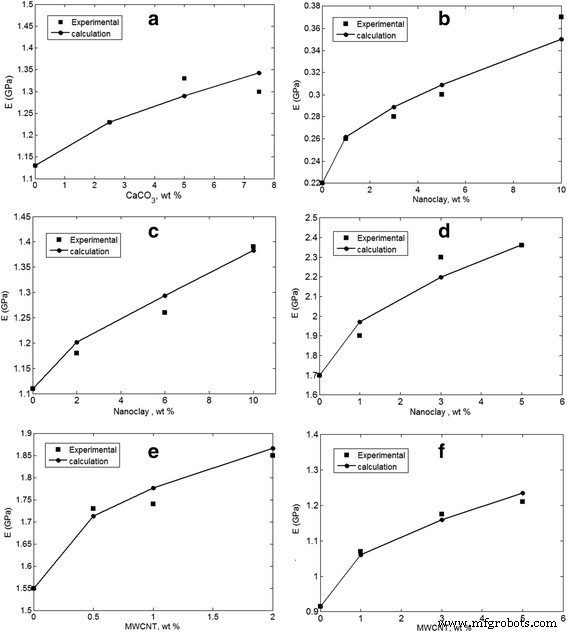
La différence entre les résultats expérimentaux et théoriques en supposant l'agrégation/agglomération de nanoparticules pour a PVC/CaCO₃ [30], b PCL/nanoargile [31], c ABS/nanoargile [32], d PLA/nanoargile [33], e PET/MWCNT [34], et f échantillons de polyimide/MWCNT [35]

Les modules les plus élevés et les plus petits prédits par la méthodologie actuelle sont calculés et illustrés sur la figure 3 à un E moyen _m = 2 GPa et E _f = 200 GPa. Le module maximum est obtenu par les plus petites valeurs de « z " et " y " paramètres; par exemple, z = 0.00001 et y = 0.00001 (ils ne peuvent pas être 0). D'autre part, le « y ” un niveau de 0,99 entraîne l'agrégation/agglomération de toutes les nanoparticules, ce qui réduit considérablement le module. De plus, le plus haut niveau de « z ” (étendue maximale d'agglomération) provoque le module minimum. « z ” car la fraction volumique de charge agglomérée dans le nanocomposite est inférieure à la fraction volumique de toutes les nanoparticules (ϕ _f ). Alors, z = ϕ _f peut suggérer le moindre niveau de module. La différence significative entre les valeurs supérieures et inférieures du module montre le rôle important de l'agrégation/agglomération des nanoparticules dans la rigidité des nanocomposites. L'agrégation/agglomération de nanoparticules dans les nanocomposites diminue considérablement le module de Young à différentes concentrations de charge, tandis qu'une fine dispersion de nanoparticules sans agrégation/agglomération produit un bon module. En outre, la forte agrégation/agglomération à de grandes teneurs en nanocharges diminue le taux de croissance du module lors de l'augmentation de "ϕ _f ”. Par conséquent, il est important d'ajuster le matériau et les paramètres de traitement pour empêcher l'agrégation/l'agglomération de nanoparticules qui favorisent la concentration de contraintes et les défauts ou le décollement dans les nanocomposites polymères [37, 38].

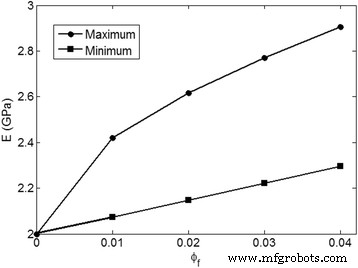
Les niveaux de module maximum et minimum prédits par la méthodologie actuelle à E moyen _m = 2 GPa et E _f = 200 GPa

La figure 4 illustre les effets de « z " et " y ” paramètres sur le module à E _m = 3 GPa, E _f = 150 GPa, et ϕ _f =0,02. Le module le plus élevé est obtenu aux plus petits niveaux de « z " et " y », confirmant le rôle positif d'une bonne dispersion/répartition des nanoparticules sur le module des nanocomposites. Cependant, le module diminue fortement lorsque « y ” augmente. Selon l'éq. 2, "y ” montre la concentration de nanoparticules dans la phase d'agglomération/agrégation. Un faible module est observé à haut "y », qui montre qu'une fraction importante de nanoparticules en phase d'agglomération/agrégation fragilise un nanocomposite. En conséquence, les nanoparticules agglomérées/agrégées provoquent un effet négatif sur le module des nanocomposites. Par conséquent, beaucoup d'efforts devraient être faits pour faciliter la dispersion/distribution des nanoparticules dans la matrice polymère, qui dépend de l'interaction/adhérence interfaciale entre le polymère et les nanoparticules et les paramètres de traitement. Des études antérieures ont rapporté des résultats précieux dans ce domaine et ont suggéré diverses techniques pour améliorer cette dispersion [39,40,41].

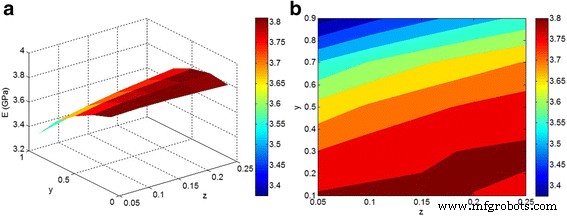
un , b Les calculs de module par Eqs. 10–11 en fonction de « z " et " y ” à E _m = 3 GPa, E _f = 150 GPa, et ϕ _f = 0,02

La figure 5 montre la dépendance du module prédit sur « E _m " et " E _f ” paramètres en moyenne ϕ _f = 0.02, z = 0.3, et y = 0,5 avec la technique actuelle. On observe que le module dépend à la fois de « E _m " et " E _f ” facteurs à faible E _f < 150 GPa. Cependant, un module plus élevé de nanoparticules ne modifie pas le module du nanocomposite. De ce fait, le module des nanocomposites ne dépend que de « E _m " lorsque "E _f " est supérieur à 150 GPa. Cela suggère que la rigidité élevée des nanoparticules ne joue pas un rôle principal dans le module nanocomposite, et une grande attention doit être accordée à la dispersion/agrégation/agglomération des nanoparticules.

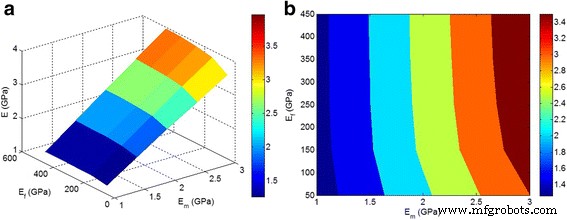
un , b Les effets de « E _m " et " E _f ” sur le module prédit par les Eqs. 10–11 en moyenne ϕ _f = 0.02, z = 0.3, et y = 0,5

Conclusions

Une technique en deux étapes a été suggérée pour déterminer les influences des nanoparticules agrégées/agglomérées sur le module de Young des nanocomposites polymères. Les modèles de Paul et Maxwell ont été appliqués pour calculer les modules d'agrégation/agglomération et les phases matricielles effectives. Les prédictions de la méthodologie suggérée ont montré un bon accord avec les données expérimentales de différents échantillons, en supposant des paramètres d'agrégation/agglomération corrects. En conséquence, la présente méthodologie peut donner des résultats acceptables pour l'agrégation/l'agglomération de nanoparticules dans des nanocomposites polymères. L'agrégation/agglomération de nanoparticules a significativement diminué le module de Young, alors qu'une fine dispersion de nanoparticules a produit un module élevé. Le module le plus élevé a été obtenu au plus petit "z " et " y », qui ont confirmé le rôle positif d'une bonne dispersion/répartition des nanoparticules dans le module des nanocomposites. Cependant, le module diminue à mesure que le « y ” paramètre augmenté. De plus, il a été constaté que les excellentes caractéristiques des nanoparticules telles que le module élevé ne sont pas suffisantes pour obtenir les propriétés optimales des nanocomposites polymères. En conséquence, une grande attention doit être portée sur la dispersion/distribution des nanoparticules dans la matrice polymère en fonction de l'interaction/adhérence interfaciale entre le polymère et les nanoparticules et les paramètres de traitement.

Vésicules éthosomales biocompatibles acide 5-aminolévulinique/Au chargées de nanoparticules pour la thérapie photodynamique/photothermique synergique transdermique in vitro des cicatrices hypertr… Effet des nanoparticules manufacturées sur la libération de substances exopolymères du phytoplancton marin

Nanomatériaux