Une étude sur les nanofibres de carbone et le charbon actif en tant que supercondensateur symétrique dans l'électrolyte aqueux :une étude comparative

Contexte

Les supercondensateurs ou condensateurs électrochimiques ont suscité beaucoup d'intérêt en raison de leur densité de puissance élevée et de leurs capacités à long cycle. Ils ont trouvé des applications potentielles dans les véhicules électriques, les appareils portables et les outils électriques [1]. Les véhicules électriques ont besoin d'une puissance élevée à un taux de drainage de courant élevé, tandis que les systèmes de sauvegarde de mémoire nécessitent une densité d'énergie élevée à un taux de drainage de courant faible. Par conséquent, le matériau doit être choisi en fonction des applications souhaitées [2]. Les principaux composants d'un supercondensateur sont les électrodes et l'électrolyte. Étant donné que le stockage de charge a lieu à l'interface électrode/électrolyte, la surface de l'électrode et de l'électrolyte utilisé influencera grandement les performances de l'appareil. Les propriétés des électrodes similaires, la nature du matériau, l'épaisseur de l'électrode, la surface, la distribution de la taille des pores et les groupes de surface influencent fortement les performances du supercondensateur [3]. Les matériaux carbonés sont largement utilisés comme électrodes en raison de leur faible coût, de la diversité de morphologies disponibles et de leur stabilité chimique et thermique [4,5,6,7]. La morphologie tubulaire CNF à l'échelle nanométrique peut offrir une combinaison unique de faible résistivité électrique et de porosité élevée dans une structure facilement accessible [8]. Un matériau AC est un matériau très attrayant pour les supercondensateurs en raison de sa porosité élevée, de son faible coût, de son abondance, de sa stabilité élevée et de ses cycles de charge-décharge [9]. La fabrication d'électrodes (AC ou CNF) pour les supercondensateurs nécessite l'ajout de liant - par exemple, le poly(tétrafluoroéthylène) (PTFE), le chlorure de polyvynilidène (PVDC) et le fluorure de polyvynilidène (PVDF) - dans des proportions qui varient généralement de 5 à 10 wt . % afin de maintenir l'intégrité des électrodes [10, 11]. Cependant, le liant bloque la partie de la porosité du carbone et provoque en outre une augmentation de la résistivité électrique [11,12,13].

La capacité du supercondensateur est fortement liée au matériau de l'électrode et à l'électrolyte. La compatibilité de l'électrolyte avec le matériau de l'électrode joue également un rôle crucial dans le développement du supercondensateur car la double couche électrique est construite à l'interface électrode/électrolyte. La tension d'un supercondensateur dépend de la fenêtre de potentiel de stabilité de l'électrolyte. Les électrolytes aqueux fournissent généralement un potentiel jusqu'à 1,0 V et un électrolyte organique jusqu'à 2,7 V [14]. Les électrolytes aqueux sont respectueux de l'environnement, alors que les électrolytes organiques ne sont pas bons pour l'environnement. Les électrolytes aqueux sont principalement composés de petits anions et de cations hydratés simples (niveau angström). Ces ions peuvent facilement pénétrer dans les micropores, les mésopores et les macropores du matériau sous le champ électrique appliqué. La double couche électrique (EDL) construite au niveau de la région interfaciale électrode/électrolyte peut être traitée comme un condensateur avec un condensateur électrique à double couche (EDLC), qui peut être exprimé par C = ϵA /d . Où ϵ est la constante diélectrique de l'électrolyte, A est la surface accessible aux ions, et d est la distance entre les ions et la surface des pores de l'électrode en carbone de l'ordre de l'angström. Selon l'équation ci-dessus, deux approches peuvent être adoptées pour améliorer efficacement le stockage de charge de l'EDLC :augmenter la SSA et réduire la distance entre les ions et la surface du carbone par le développement [15].

Dans ce travail, l'objectif est de fournir une analyse comparative des supercondensateurs symétriques basés sur AC et CNF en utilisant une quantité similaire de liant PVDF 7% en poids pour les deux matériaux.

Méthodes/Expérimental

Préparation des électrodes AC et CNF

Un supercondensateur symétrique basé sur AC et CNF a été préparé à des fins de comparaison. La référence AC Carbopal CCP80 de Donau Carbon est fournie par QuimicsDalmau. Les CNF ont une structure en cupule empilée graphitique hélicoïdale, il y a une présence de Ni (6%), le diamètre est de 20-80 nm, la longueur (MEB)> 30um et la résistivité électrique de 10 ⁻² Ω cm.

Le PVDF a été utilisé comme liant. Afin de comparer la préparation des électrodes pour l'analyse des supercondensateurs pour les deux matériaux (AC, CNF) a été réalisée de manière similaire en suivant les étapes ci-dessous.

Etape 1 :Broyage de (AC ou CNFs) dans un broyeur planétaire à billes de zircone (Pulverisette 7 de Fritch) employant une fréquence de 500 rpm pendant 30 min. Étape 2 :Mélange d'AC ou de CNF à 93 % en poids avec 7 % en poids de polymère PVDF en utilisant 15 ml d'acétone dans un mortier d'agate. Étape 3 :La suspension a ensuite été mélangée à l'aide d'un agitateur mécanique pendant 60 min suivi d'un ultrasons pendant 30 min. Étape 4 :La suspension du mélange a été séchée dans un four pendant 60 minutes à 70 °C. Étape 5 :Dans la dernière étape, la suspension séchée a été utilisée pour préparer les électrodes, en quelque sorte, à l'aide d'une presse hydraulique avec une matrice (10 mm) à une force de 10 tonnes. La masse calculée des disques d'électrodes préparés sur la base des CNF et de l'AC était respectivement de 0,018 et 0,02 g.

Caractérisation de surface

La texture poreuse, la surface spécifique et la distribution de la taille des pores des électrodes CNF et AC ont été obtenues par adsorption physique de gazN₂ à 77 K en utilisant Micromeritics TriStar 3000 V6.04 A. Tous les échantillons ont été dégazés à 100 ° C pendant 4 h avant les mesures d'adsorption. La surface spécifique (S _PARIER , m ² /g) a été déterminé par la méthode multipoint de Brunauer-Emmett-Teller (BET) dans la région de l'isotherme, qui est limitée par la plage de pression relative P /P ₀ = 0,02–0,2. Le volume total des pores (V _total , cm ³ /g) a été calculé par le nombre d'azote adsorbé à P /P ₀ ≈ 0.9932. Le volume des micropores et les valeurs des surfaces de micro (S _micro , m ² /g) ont été étudiés à l'aide de la méthode t-plot (Harkins et Jura) ; la distribution de la taille des pores pour l'échantillon CNF est calculée à partir des isothermes d'adsorption par la méthode Barrett-Joyner-Halenda (BJH) ; et la méthode MP est utilisée pour calculer la distribution de la taille des pores pour AC.

Caractérisation morphologique

Les échantillons AC et CNF ont été examinés par microscopie électronique à balayage (MEB). Les analyses MET ont été effectuées sur un système Philips Tecnai G2 F20 fonctionnant à 300 kV. Les échantillons ont été mis en suspension dans de l'éthanol et dispersés par ultrasons pendant 15 min. Une goutte de la suspension a été déposée sur une grille de cuivre recouverte de carbone.

Caractérisation électrochimique

La comparaison des performances électrochimiques de l'AC et des CNF en tant que condensateurs symétriques a été étudiée dans des cellules Swagelok à deux électrodes et en utilisant un potentiostat Gamry 600 utilisant une solution de KOH 6-M comme électrolyte. La capacité spécifique des matériaux d'électrode a été étudiée par voltamétrie cyclique (CV), charge/décharge galvanostatique (GCD) et spectroscopie d'impédance électrochimique (EIS).

Résultats et discussion

Caractérisation morphologique

La morphologie de surface des électrodes préparées a été étudiée par SEM Fig. 1 et TEM Fig. 1 (en médaillon). On peut voir clairement que le liant PVDF lie efficacement les CNF Fig. 1a et AC Fig. 1b. Les différentes structures pour les deux électrodes de CNF et AC sont visibles. La structure CNF typique, la forme cylindrique et la structure des cristaux en médaillon Fig. 1a. L'image MET d'AC montre des sphères interconnectées avec une taille homogène et une surface plus lisse en médaillon Fig. 1b.

Images SEM et images TEM (en médaillon) pour a CNF et b CA

Texture des pores des CNF et AC

Le N₂ L'isotherme d'adsorption/désorption des CNF et de l'AC est illustré à la figure 2. Les distributions de volume et de taille de pores ont été calculées par la méthode BJH, la méthode t-plot et la méthode MP. Seule l'analyse par la méthode MP peut révéler la fine différence de distribution de la taille des micropores de l'échantillon [16]. La distribution de la taille des pores des matériaux est classée en trois groupes :les micropores (< 2 nm), les mésopores (2–50 nm) et les macropores (> 50 nm) [17]. L'isotherme des CNF présente une petite boucle d'hystérésis de la plage de pression supérieure à moyenne, ce qui indique que les CNF contiennent une structure mésoporeuse. Pour cette raison, seule la méthode BJH est utilisée pour la détection de la taille des pores, car la méthode MP ne peut pas détecter la méso- et la macroporosité. Selon la classification IUPAC, l'isotherme des CNF peut être classée comme isotherme de type II. La distribution des pores des CNF est la suivante :59 % de mésopores (2 à 50 nm), 17,9 % de micropores (0,5 à 2 nm) et 23 % de macropores (> 50 nm). Les détails sont présentés dans le tableau 1.

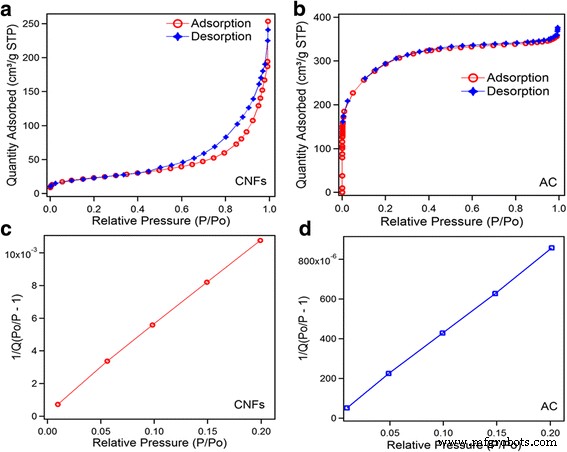
Isothermes d'adsorption/désorption d'azote, a CNF et b CA. Surface BET c CNFS et d CA

L'isotherme d'adsorption/désorption AC présente que la majeure partie de la quantité d'adsorption a lieu à une pression relative très faible (P /P ₀ ≤ 0,02) et un plateau de pression relative faible à élevée (0,6–0,8). Le volume poreux total est de 0,582 cm ³ /g à pression relative (P /P ₀ = 0.9932). La figure 2b présente que la courbure de l'isotherme de 0 à 0,4 pression relative présente un volume poreux pour moins de 50 nm de pores (micro + méso), et ce volume poreux est égal à 0,534 cm ³ /g qui est l'indication d'une structure très microporeuse. Le système d'isotherme d'échantillon AC est classé comme isotherme de type I. La distribution des pores de l'AC est la suivante :les supermicropores (0,5 à 2 nm) occupaient 33 %, les ultramicro (0,2 à 0,5 nm) occupaient 55 % et les mésopores occupaient 12 %. La méthode MP a été utilisée pour la détection de la taille des pores AC car la méthode BJH ne peut pas détecter la microporosité AC. Les détails sont présentés dans le tableau 1.

La surface spécifique (BET) a été déterminée par la méthode de Brunauer-Emmett-Teller (BET) à points multiples dans la région de l'isotherme, qui est limitée par la plage de pression relative P /P ₀ =0,02–0,2 comme le montre la Fig. 2c, d. Le volume total des pores (V_total , cm ² /g) a été calculé par le nombre d'azote adsorbé à P /P ₀ ≈ 0.9932. Le volume d'adsorption montre que les surfaces BET pour les CNF et AC sont de 83 et 1042 m ² /g, respectivement.

Les analyses de distribution de la taille des pores sont présentées dans les Fig. 3a, b obtenues via la méthode MP pour AC et en utilisant la méthode Barrett-Joiner-Halenda (BJH) pour les CNF. Les CNF contiennent deux types de pores dominants centrés dans les plages de 3,36 et 7,1 nm, tandis que l'AC est principalement composé de pores de 0,47 nm. Les microspores sont bénéfiques pour une accumulation de charge dans les électrolytes aqueux [18, 19]. On peut voir que pour les CNF, les pores les plus dominants sont des mésopores tandis que pour les ultra-micropores AC.

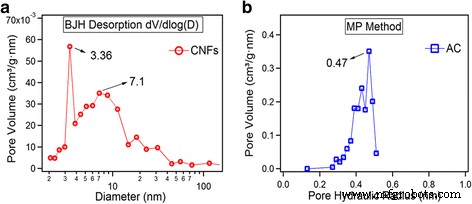
Distribution de la taille des pores. un CNF par la méthode BJH. b Méthode AC par MP

Comportement électrochimique des CNF et AC

Les principales approches acceptées pour évaluer la capacité du supercondensateur sont la voltamétrie cyclique, la charge/décharge galvanostatique et la spectroscopie d'impédance. Le principe de fonctionnement de chaque technique varie de l'une à l'autre. Le comportement électrochimique de l'AC et des CNF a d'abord été caractérisé par voltamétrie cyclique dans la plage de 0 à 1 V. CV est la méthode la plus pratique pour caractériser le comportement capacitif des matériaux d'électrode. La capacité spécifique par unité de masse pour une électrode a été calculée en utilisant les équations. (1, 2).

Où C _s est la capacité spécifique en F/g, C est la capacité mesurée pour la cellule à deux électrodes par l'équation. 2, et m est la masse totale du matériau actif dans les deux électrodes [20].

La figure 4a, b montre les CV des CNF et AC, respectivement, de 5 à 500 mV/s taux de balayage. Les CV des CNF dans une large gamme de taux de balayage sont presque en forme de boîte sans aucune bosse, ou une déviation indique des caractéristiques claires à double couche et une réversibilité élevée. Les CV pour AC montrent un courant beaucoup plus élevé que les CNF. À de faibles taux de balayage, la forme du CV est rectangulaire, ce qui montre que la réponse de l'électrode lors de la charge et de la décharge est hautement réversible. Cependant, à des taux de balayage plus élevés, CV s'écarte d'une forme rectangulaire. Il pourrait y avoir plusieurs raisons possibles liées à cet écart, (1) en raison de la faible conductivité électrique de la structure poreuse du courant alternatif des pores internes qui ne sont pas accessibles aux ions et (2) une constante de temps non nulle et un courant transitoire élevé, ce qui entraîne un condensateur plus long temps de charge et un effondrement de la forme rectangulaire [21, 22].

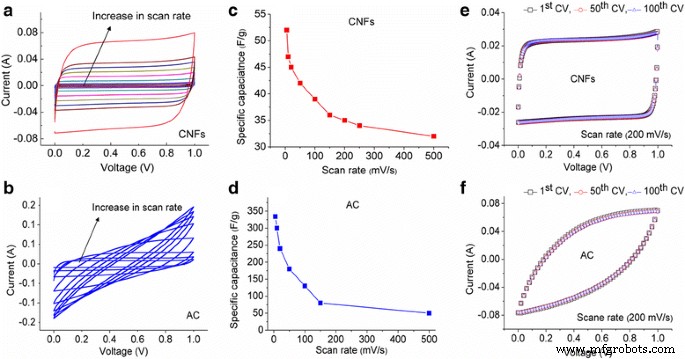
un , b CV des CNF et AC, respectivement, à des taux de balayage de 5, 10, 20, 50, 100, 150 et 500 mV/s ; c , d comparaison de capacité spécifique à différentes vitesses de balayage ; e , f CV des CNF et AC, respectivement, du 1er au 100e cycle

La figure 4c, d présente la comparaison de capacité spécifique des CNF et du courant alternatif à des taux de balayage de 5 à 500 mV/s. Comme on peut le voir sur la figure 4c, les CNF présentent la capacité spécifique la plus élevée de 52 F/g à une vitesse de balayage de 5 mV/s. La capacité spécifique a diminué à 32 F/g à une vitesse de balayage de 500 mV/s. Ces résultats indiquent la diminution modérée de la capacité spécifique, et à des vitesses de balayage encore plus élevées, la plupart de la surface et des pores des CNF sont accessibles aux ions. La capacité du courant alternatif passe de 334 à 50 F/g pour 5 à 500 mV/s Fig. 4d. La capacité spécifique très élevée à faible taux de balayage est due au fait que les ions ont suffisamment de temps pour pénétrer profondément à l'intérieur de la structure microporeuse (moins de 2 nm) du courant alternatif. On peut supposer qu'à des vitesses de balayage plus élevées, la plupart des mésopores à pores plus grands (2 à 50 nm) contribuent à la capacité. Ceci est principalement dû à la différence de taux de diffusion de l'électrolyte dans les pores de tailles différentes et également à la connexion réseau entre les pores grands et petits [23]. Comme discuté par A.G. Pandolofo et al., la surface mesurée est due à tous les pores ouverts, mais tous les pores ne sont pas accessibles par voie électrochimique [8].

La capacité spécifique plus élevée du courant alternatif par rapport aux CNF pourrait être due à la surface plus élevée, ce qui entraîne une augmentation des zones accessibles aux ions électrolytiques pour le stockage de charge dans des pores relativement petits.

Les courbes CV des CNF et AC (Fig. 4e, f) indiquent un comportement de capacité stable mesuré jusqu'au 100e cycle à une vitesse de balayage de 200 mV/s. Le 100e cycle CV pour les deux échantillons conserve la forme telle qu'elle était pour le 1er cycle suggère une excellente stabilité et des processus d'électrode réversibles.

Les performances supercapacitives des CNF et AC ont été comparées par GCD, comme le montrent les figures 5a, b. La capacité de décharge (C ) est estimée à partir de la pente (dV/dt ) de la partie linéaire de la courbe de débit en utilisant l'Eq. 3.

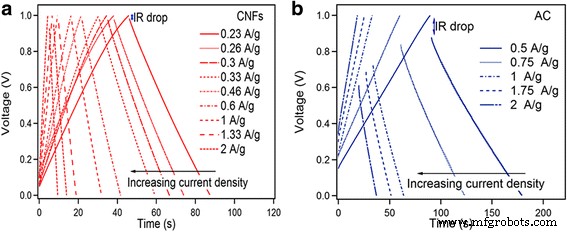
un Courbes GCD à différentes densités de courant de CNF. b Courbes GCD à différentes densités de courant AC

Où C _s est la capacité spécifique en F/g, ∆V est la différence de tension pendant la courbe de décharge en V , Je est le courant dans A , et ∆t est le temps de décharge en s .

On peut voir que les processus de charge et de décharge sont presque symétriques, indiquant une excellente réversibilité électrochimique des électrodes. Les courbes de décharge des CNF montrent un petit IR chute impliquant une faible résistance série équivalente, ce qui est essentiel à la caractéristique de puissance des supercondensateurs. Le IR inférieur la chute des CNF vers le courant alternatif est due à la conductivité élevée des CNF. Le grand IR chute pour AC signifie une résistance série équivalente (ESR) plus élevée. La capacité spécifique calculée pour les CNF 23,8 F/g à 0,23 A/g diminue à 19 F/g à 2 A/g. La capacité spécifique du courant alternatif passe de 159 F/g à une densité de courant de 0,5 A/g à 139 F/g à 2,5 A/g Fig. 6a. La capacité spécifique des deux condensateurs symétriques des CNF et du courant alternatif diminue avec l'augmentation de la densité de courant, ce qui est très courant pour les supercondensateurs et est principalement causé par la limitation de la diffusion des ions électrolytes dans les microspores de l'électrode.

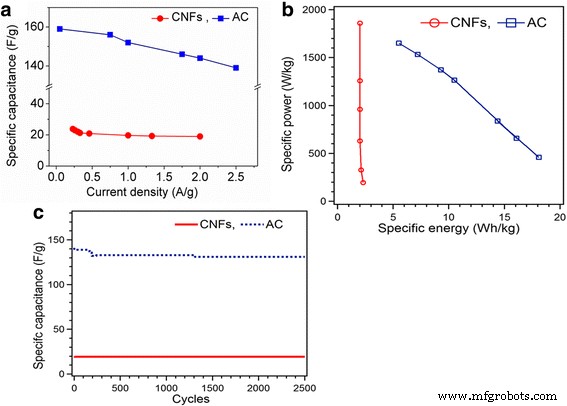
un Comparaison de capacité spécifique à partir de la courbe de décharge du GCD. b Graphique de Ragone de la puissance spécifique par rapport à l'énergie spécifique pour les CNF et le courant alternatif. c Stabilité cyclable des CNF et AC

La puissance spécifique, P , et l'énergie spécifique, E, délivrée lors de la décharge ont été estimées par les équations. (4) et (5).

Où V est la tension hors IR déposer, i est le courant de décharge, et t est l'heure [24].

Comme on peut le voir dans le graphique de Ragone Fig. 6b, l'électrode CNF montre une énergie spécifique maximale de 2,3 Wh/kg à une puissance spécifique de 197 W/kg et une densité de puissance maximale de 1860 W/kg à une énergie spécifique de 2 Wh/kg indiquant ses bonnes caractéristiques de puissance. Ces résultats montrent une augmentation de la puissance spécifique; l'énergie spécifique ne diminue que légèrement, ce qui est une signature d'excellentes propriétés électrochimiques de densité d'énergie et de puissance de sortie élevées, donc très prometteuse pour une application dans les scénarios où une puissance de sortie élevée ainsi qu'une capacité énergétique élevée sont requises [25]. Pour le courant alternatif avec l'augmentation de la puissance spécifique de 459 à 1650 W/kg, l'énergie spécifique a diminué de 18,1 à 5,5 Wh/kg.

La stabilité en cyclisme est également un facteur vital pour les applications pratiques. La mesure du cycle de charge-décharge galvanostatique a été effectuée à une densité de courant constante de 2 A/g pour le courant alternatif et pour les CNF jusqu'à 2500 cycles. Fig. 6c. Le comportement du courant alternatif pendant la stabilité du cycle montre une petite diminution de la capacité de 141 à 131 F/g en 2500 cycles. Ce résultat exprime que l'évanouissement de la capacité est dû aux réactions irréversibles au début du cyclage [10]. Les mesures de cyclage CNF révèlent une excellente rétention de capacité de 19 F/g en 2500 cycles.

Le supercondensateur a ensuite été analysé par spectroscopie d'impédance électrochimique (EIS). Il représente le tracé de Nyquist dans la gamme de fréquences de 10 kHz à 0,1 Hz pour les CNF et le courant alternatif (Fig. 7a). Les tracés de Nyquist consistent en (1) une intersection à haute fréquence sur l'axe Z' réel, (2) un demi-cercle dans la région des hautes à moyennes fréquences, et (3) une ligne droite à la très basse fréquence région [26]. Dans la région des hautes fréquences, les interceptions avec Z' des CNF et AC sont respectivement de 0,11 et 0,16 . Cette valeur est considérée comme la résistance électrique totale du matériau de l'électrode, de l'électrolyte et des contacts électriques [27]. Le demi-cercle de haute à moyenne fréquence correspond à une combinaison parallèle de résistance de transfert de charge (R _ct ) et la capacité double couche [28]. On voit que le demi-cercle (R _ct ) est plus élevé pour AC (3,56 ) que pour les CNF (0,17 ). Les ESR calculées étaient de 0,28 et 3,72 Ω pour les CNF et les AC, respectivement. La très petite valeur de l'ESR pour les CNF, par rapport à AC, indique la facilité de transport/diffusion des électrons et des ions dans les électrodes CNF. Cela indique que l'électrode CNF a une conductivité beaucoup plus élevée que l'électrode AC. Comme également observé sur la figure 7a, les CNF ont montré une pente plus élevée de la ligne droite, dans la gamme des basses fréquences, que le courant alternatif. Cela signifie que les CNF présentent un comportement capacitif plus élevé que le courant alternatif.

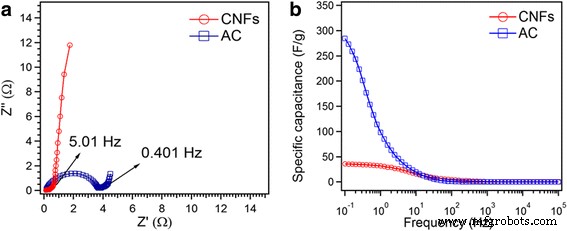
un Parcelle de Nyquist des CNF et AC. b Comparaison Csp calculée à partir de l'EIS.

La capacité spécifique, C _s , du supercondensateur CNF et AC a également été calculé à partir de l'analyse d'impédance utilisant la composante imaginaire de l'impédance en suivant l'équation [29].

Où f est la fréquence en Hz, z ” est la composante imaginaire de l'impédance, et m est la masse de CNF ou AC calculée pour une électrode. La figure 7b montre le changement plus important de la capacité spécifique des CNF et du courant alternatif en dessous de la fréquence de 10 Hz. La capacité spécifique obtenue pour les CNF (36 F/g) et AC (284 F/g) à la fréquence de 0,1 Hz est à peu près comparable à la capacité calculée par CV. En effet, une capacité spécifique plus élevée pour le courant alternatif est due à une plus grande surface disponible pour l'accumulation de charge à l'interface solide-liquide.

Constante de temps τ est la propriété du supercondensateur qui reflète la réponse de l'appareil. Une petite valeur de τ donne une indication d'une meilleure réponse. La constante de temps τ a été calculé à l'aide de l'équation suivante :

Où E _D est la densité d'énergie et P _D est la densité de puissance. E _D et P _D ont été calculés à l'aide des équations suivantes :

Où V est la fenêtre de tension pendant la courbe de décharge de charge, C est la capacité de la charge-décharge et de l'ESR calculée à partir de la spectroscopie d'impédance, et m est la masse de l'électrode. La constante de temps calculée τ pour AC était de 3,1 s et pour les CNF était de 0,08 s à une densité de courant de 2 A/g, indiquant une meilleure réponse capacitive pour les CNF.

La relation entre Z _réel et la fréquence nous donne des informations sur l'électrolyte et la résistance de transfert de charge dans l'électrolyte Fig. 8a. Le comportement de résistance de l'électrode est fortement influencé par la nature de l'électrode en carbone. Pour les CNF et les AC à haute fréquence 100 KHz, l'ESR est à ses valeurs les plus basses de l'ordre d'environ 0,1 , ce qui présente la résistance électrolytique R s. En abaissant la fréquence, jusqu'à 506 Hz, il y a une forte augmentation de la résistance du courant alternatif par rapport aux CNF. À la fréquence observée la plus basse (0,1 Hz), l'ESR avait une valeur de 1,87 et 4,5 pour AC et CNF, respectivement. L'augmentation de l'ESR avec la diminution de la fréquence pourrait être due à la difficulté de pénétration du signal électrique dans les pores plus profonds (remplis d'électrolyte) et/ou dans les particules plus petites [30]. Cette variation peut être justifiée par le fait que lorsque la fréquence diminue, les ions peuvent facilement atteindre les zones plus profondes des pores du charbon actif, et par conséquent, leur déplacement plus long dans l'électrolyte entraîne une résistance électrolytique plus élevée [31].

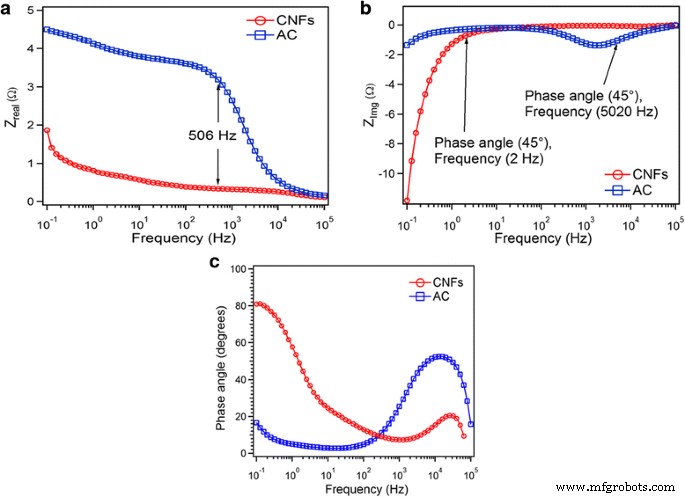
un Le réel et b les parties imaginaires sont tracées en fonction du log de fréquence et c déphasage en fonction de la fréquence pour AC et CNF

La relation entre Z _Img et la fréquence nous renseignent sur le temps de relaxation (τ ₀ ) dans la région limite, où le supercondensateur passe de la résistance au condensateur Fig. 8b. La constante de temps τ ₀ qui correspond à l'angle de phase 45° représente la transition du condensateur électrochimique d'un comportement purement résistif à purement capacitif. Il est bien connu qu'une puissance délivrée plus élevée correspond à une τ plus faible ₀ valeurs. Pour la fréquence, f > 1/τ ₀ , il agit comme une résistance pure, et pour f < 1/τ ₀ , il se comporte comme un pur condensateur. L'angle de phase de 45° a été trouvé pour le courant alternatif à la fréquence 5020 Hz et pour les CNF à 1,99 Hz. Cela montre que le temps de relaxation pour les AC est bien inférieur à celui des CNF. Par conséquent, la traduction du comportement résistif en comportement capacitif pour le courant alternatif est beaucoup plus rapide que les CNF.

La figure 8c représente la variation de l'angle de phase en fonction de la fréquence, connue sous le nom de tracé de Bode. Les angles de phase sont respectivement de − 20° et − 88° à basse fréquence 0,1 Hz dans les systèmes AC et CNF (Fig. 8c). En général, l'approche de l'angle de phase à - 90° confirme de meilleures performances capacitives et un processus de charge-décharge rapide. La constante de temps de relaxation, τ 0, définit le temps nécessaire pour délivrer efficacement la charge stockée, comme le montre la figure 8b [32].

Effet de la structure du carbone et de la texture poreuse sur les performances EDLC

D'après la caractérisation électrochimique, il est évident que le supercondensateur basé sur des électrodes AC donne une capacité spécifique plus élevée que les CNF dans l'électrolyte KOH 6-M. D'après l'équation, =  ∈ A /d , distance (d ) est très faible lorsque l'électrode contient des micropores. La capacité plus élevée du courant alternatif est due à certaines propriétés importantes, à savoir une surface BET plus élevée et l'existence de 88 % plus élevés d'ultramicropores et de micropores. Alors que les échantillons de CNF ont une faible surface BET et 17,9% de micropores. Un autre facteur important qui influence la capacité est lié à l'équation suivante, τ = L ² /D . Où L fait référence à la longueur de transport des ions, et D fait référence au coefficient de transport d'ions. Selon cette équation, les ions pénètrent rapidement à l'intérieur des micropores, mais à mesure que la taille des pores augmente, la surface externe augmente également. De ce fait, les ions s'accumulent à l'extérieur des pores, entraînant ainsi la diminution de la capacité. D'après E. Raymundo-Pinero et al., en solution aqueuse, la formation de double couche est très favorable lorsque la taille des pores est d'environ 0,7 nm [19]. Nos résultats révèlent que la taille des pores du courant alternatif (0,47 nm) se situe dans la plage optimale pour construire la double couche, et présente donc une capacité spécifique plus élevée que les CNF.

Conclusions

Les électrodes CNF et AC ont été préparées selon une technique similaire et comparées en tant que supercondensateur symétrique utilisant une solution aqueuse. La distribution de la taille des pores, la surface de l'électrode et la résistance totale de l'électrode se sont avérées jouer un rôle crucial dans la détermination des performances du supercondensateur. Les résultats du BET révèlent que l'AC a un nombre élevé de micropores et une structure ultramicroporeuse qui donne une surface de 1042 m ² /g, alors que l'électrode CNF contient une structure mésosporée dominante et une surface de 83 m ² /g. De ce fait, le matériau AC délivre une capacité spécifique (334 F/g) bien supérieure aux CNF (52 F/g). En effet, une capacité spécifique plus élevée pour le courant alternatif a donné une énergie spécifique plus élevée (18,1 Wh/kg) que celle pour les CNF (2 Wh/kg). D'autre part, les CNF révèlent une ESR plus faible (0,28 ) que l'AC (3,72 ). Les puissances spécifiques obtenues en fonction de la valeur ESR étaient de 1860 et 450 W/kg pour les CNF et AC, respectivement. Par conséquent, le courant alternatif est considéré comme approprié pour les applications énergétiques. Considérant que, CNF est un meilleur candidat pour les applications de puissance.