MATLAB - Transforme

MATLAB fournit une commande pour travailler avec des transformations, telles que les transformations de Laplace et de Fourier. Les transformations sont utilisées en science et en ingénierie comme outil pour simplifier l'analyse et examiner les données sous un autre angle.

Par exemple, la transformée de Fourier permet de convertir un signal représenté en fonction du temps en une fonction de fréquence. La transformée de Laplace nous permet de convertir une équation différentielle en une équation algébrique.

MATLAB fournit le laplace , fournier et fft commandes pour travailler avec les transformées de Laplace, de Fourier et de Fourier rapide.

La transformée de Laplace

La transformée de Laplace d'une fonction du temps f(t) est donnée par l'intégrale suivante −

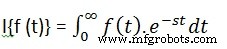
La transformée de Laplace est également notée transformée de f(t) en F(s). Vous pouvez voir que ce processus de transformation ou d'intégration convertit f(t), une fonction de la variable symbolique t, en une autre fonction F(s), avec une autre variable s.

La transformée de Laplace transforme les équations différentielles en équations algébriques. Pour calculer une transformée de Laplace d'une fonction f(t), écrivez −

laplace(f(t))

Exemple

Dans cet exemple, nous allons calculer la transformée de Laplace de certaines fonctions couramment utilisées.

Créez un fichier de script et tapez le code suivant −

syms s t a b w

laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

Lorsque vous exécutez le fichier, il affiche le résultat suivant −

ans =
   1/s^2

ans =
   2/s^3

ans =
   362880/s^10

ans =
   1/(b + s)
  
ans =
   w/(s^2 + w^2)
  
ans =
   s/(s^2 + w^2)

La transformée inverse de Laplace

MATLAB nous permet de calculer la transformée de Laplace inverse à l'aide de la commande ilaplace .

Par exemple,

ilaplace(1/s^3)

MATLAB exécutera l'instruction ci-dessus et affichera le résultat −

ans =
   t^2/2

Exemple

Créez un fichier de script et tapez le code suivant −

syms s t a b w

ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

Lorsque vous exécutez le fichier, il affiche le résultat suivant −

ans =
   t^6/720

ans =
   2*exp(-t*w)

ans =
   cos(2*t)

ans =
   ilaplace(exp(-b*t), t, x)

ans =
   sin(t*w)

ans =
   cos(t*w)

Les transformées de Fourier

Les transformées de Fourier transforment généralement une fonction mathématique du temps, f(t), en une nouvelle fonction, parfois désignée par ou F, dont l'argument est la fréquence avec des unités de cycles/s (hertz) ou de radians par seconde. La nouvelle fonction est alors appelée transformée de Fourier et/ou spectre de fréquence de la fonction f.

Exemple

Créez un fichier de script et tapez-y le code suivant −

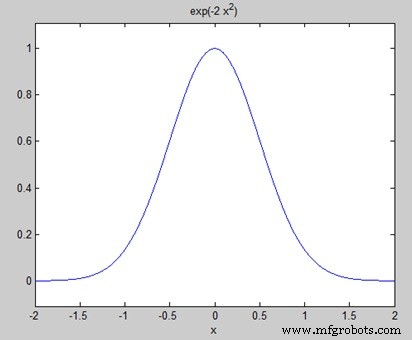
syms x 
f = exp(-2*x^2);     %our function
ezplot(f,[-2,2])     % plot of our function
FT = fourier(f)      % Fourier transform

Lorsque vous exécutez le fichier, MATLAB trace le graphique suivant −

Le résultat suivant s'affiche −

FT =
   (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

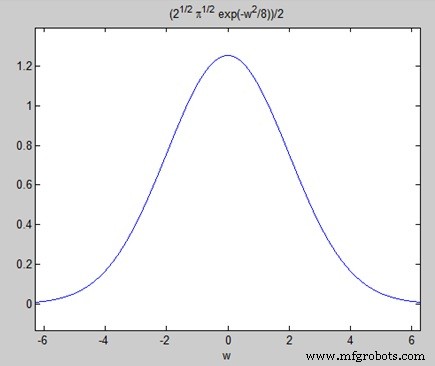
Tracer la transformée de Fourier comme −

ezplot(FT)

Donne le graphe suivant −

Transformées de Fourier inverses

MATLAB fournit le ifourier commande pour calculer la transformée de Fourier inverse d'une fonction. Par exemple,

f = ifourier(-2*exp(-abs(w)))

MATLAB exécutera l'instruction ci-dessus et affichera le résultat −

f =
   -2/(pi*(x^2 + 1))