MATLAB - Tutoriel GNU Octave

GNU Octave est un langage de programmation de haut niveau comme MATLAB et il est principalement compatible avec MATLAB. Il est également utilisé pour les calculs numériques.

Octave a les caractéristiques communes suivantes avec MATLAB −

• les matrices sont des types de données fondamentaux
• il a un support intégré pour les nombres complexes
• il a des fonctions et des bibliothèques mathématiques intégrées
• il prend en charge les fonctions définies par l'utilisateur

GNU Octave est également un logiciel librement redistribuable. Vous pouvez le redistribuer et/ou le modifier selon les termes de la licence publique générale GNU (GPL) telle que publiée par la Free Software Foundation.

MATLAB contre Octave

La plupart des programmes MATLAB s'exécutent dans Octave, mais certains programmes Octave peuvent ne pas s'exécuter dans MATLAB car Octave autorise une syntaxe que MATLAB ne permet pas.

Par exemple, MATLAB ne prend en charge que les guillemets simples, mais Octave prend en charge les guillemets simples et doubles pour définir les chaînes. Si vous recherchez un didacticiel sur Octave, veuillez parcourir ce didacticiel depuis le début, qui couvre à la fois MATLAB et Octave.

Exemples compatibles

Presque tous les exemples couverts dans ce tutoriel sont compatibles avec MATLAB ainsi qu'Octave. Essayons l'exemple suivant dans MATLAB et Octave qui produit le même résultat sans aucun changement de syntaxe −

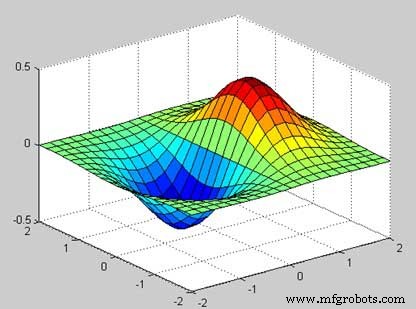
Cet exemple crée une carte de surface 3D pour la fonction g =xe ^{-(x 2 + y 2 )} . Créez un fichier de script et tapez le code suivant −

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Lorsque vous exécutez le fichier, MATLAB affiche la carte 3D suivante −

Exemples non compatibles

Bien que toutes les fonctionnalités de base de MATLAB soient disponibles dans Octave, certaines fonctionnalités, par exemple le calcul différentiel et d'intégration, ne correspondent pas exactement dans les deux langages. Ce tutoriel a essayé de donner les deux types d'exemples où ils différaient dans leur syntaxe.

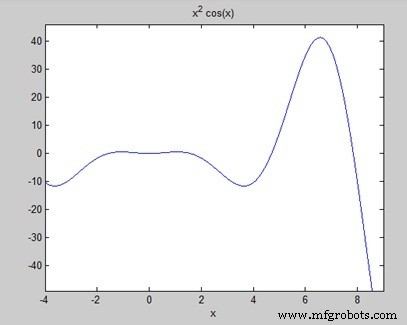
Considérez l'exemple suivant où MATLAB et Octave utilisent différentes fonctions pour obtenir l'aire d'une courbe :f(x) =x ² cos(x) pour −4 ≤ x ≤ 9. Voici la version MATLAB du code −

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Lorsque vous exécutez le fichier, MATLAB trace le graphique −

Le résultat suivant s'affiche

a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

Mais pour donner l'aire d'une même courbe dans Octave, vous devrez utiliser symbolique paquet comme suit −

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));