MATLAB - Calcul
MATLAB propose différentes manières de résoudre des problèmes de calcul différentiel et intégral, de résoudre des équations différentielles de tout degré et de calculer des limites. Mieux encore, vous pouvez facilement tracer les graphiques de fonctions complexes et vérifier les maxima, les minima et d'autres points fixes sur un graphique en résolvant la fonction d'origine, ainsi que sa dérivée.
Ce chapitre traitera des problèmes de calcul. Dans ce chapitre, nous aborderons les concepts de pré-calcul, c'est-à-dire le calcul des limites des fonctions et la vérification des propriétés des limites.
Dans le chapitre suivant Différentiel , nous allons calculer la dérivée d'une expression et trouver les maxima et minima locaux sur un graphique. Nous discuterons également de la résolution d'équations différentielles.
Enfin, dans l'Intégration chapitre, nous aborderons le calcul intégral.
Calcul des limites
MATLAB fournit la limite fonction de calcul des limites. Dans sa forme la plus élémentaire, la limite La fonction prend l'expression comme argument et trouve la limite de l'expression lorsque la variable indépendante tend vers zéro.
Par exemple, calculons la limite d'une fonction f(x) =(x 3 + 5)/(x 4 + 7), lorsque x tend vers zéro.
syms x limit((x^3 + 5)/(x^4 + 7))
MATLAB exécutera l'instruction ci-dessus et renverra le résultat suivant −
ans = 5/7
La fonction limite relève du domaine de l'informatique symbolique; vous devez utiliser les syms pour indiquer à MATLAB quelles variables symboliques vous utilisez. Vous pouvez également calculer la limite d'une fonction, car la variable tend vers un nombre autre que zéro. Pour calculer lim x->a (f(x)), nous utilisons la commande limit avec arguments. Le premier étant l'expression et le second le nombre, que x approches, le voici a .
Par exemple, calculons la limite d'une fonction f(x) =(x-3)/(x-1), lorsque x tend vers 1.
limit((x - 3)/(x-1),1)
MATLAB exécutera l'instruction ci-dessus et renverra le résultat suivant −
ans = NaN
Prenons un autre exemple,
limit(x^2 + 5, 3)
MATLAB exécutera l'instruction ci-dessus et renverra le résultat suivant −
ans = 14
Calcul des limites à l'aide d'Octave
Voici la version Octave de l'exemple ci-dessus utilisant symbolique package, essayez d'exécuter et de comparer le résultat −
pkg load symbolic
symbols
x = sym("x");
subs((x^3+5)/(x^4+7),x,0)
Octave exécutera l'instruction ci-dessus et renverra le résultat suivant −
ans = 0.7142857142857142857
Vérification des propriétés de base des limites
Le théorème algébrique des limites fournit certaines propriétés de base des limites. Ce sont les suivants −
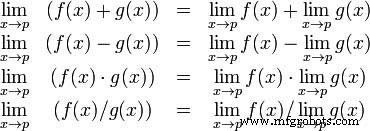
Considérons deux fonctions −
- f(x) =(3x + 5)/(x - 3)
- g(x) =x 2 + 1.
Calculons les limites des fonctions lorsque x tend vers 5, des deux fonctions et vérifions les propriétés de base des limites en utilisant ces deux fonctions et MATLAB.
Exemple
Créez un fichier de script et tapez-y le code suivant −
syms x f = (3*x + 5)/(x-3); g = x^2 + 1; l1 = limit(f, 4) l2 = limit (g, 4) lAdd = limit(f + g, 4) lSub = limit(f - g, 4) lMult = limit(f*g, 4) lDiv = limit (f/g, 4)
Lorsque vous exécutez le fichier, il affiche −
l1 = 17 l2 = 17 lAdd = 34 lSub = 0 lMult = 289 lDiv = 1
Vérification des propriétés de base des limites à l'aide d'Octave
Voici la version Octave de l'exemple ci-dessus utilisant symbolique package, essayez d'exécuter et de comparer le résultat −
pkg load symbolic
symbols
x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)
Octave exécutera l'instruction ci-dessus et renverra le résultat suivant −
l1 = 17.0 l2 = 17.0 lAdd = 34.0 lSub = 0.0 lMult = 289.0 lDiv = 1.0
Limites gauche et droite
Lorsqu'une fonction présente une discontinuité pour une valeur particulière de la variable, la limite n'existe pas à ce point. En d'autres termes, les limites d'une fonction f(x) ont une discontinuité à x =a, lorsque la valeur de la limite, lorsque x s'approche de x depuis le côté gauche, n'est pas égale à la valeur de la limite lorsque x s'approche du côté droit.
Cela conduit au concept de limites à gauche et à droite. Une limite gauche est définie comme la limite telle que x -> a, à partir de la gauche, c'est-à-dire que x s'approche de a, pour les valeurs de x
Considérons une fonction −
f(x) =(x - 3)/|x - 3|
Nous allons montrer que limx->3 f(x) n'existe pas. MATLAB nous aide à établir ce fait de deux manières −
- En traçant le graphique de la fonction et en montrant la discontinuité.
- En calculant les limites et en montrant que les deux sont différentes.
Les limites gauche et droite sont calculées en passant les chaînes de caractères 'left' et 'right' à la commande limit comme dernier argument.
Exemple
Créez un fichier de script et tapez-y le code suivant −
f = (x - 3)/abs(x-3); ezplot(f,[-1,5]) l = limit(f,x,3,'left') r = limit(f,x,3,'right')
Lorsque vous exécutez le fichier, MATLAB dessine le tracé suivant
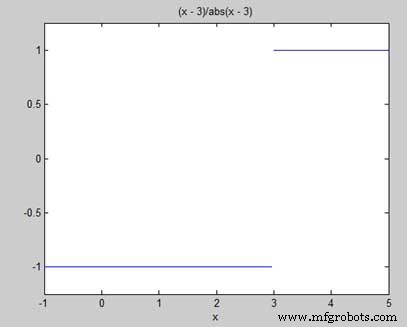
Après l'affichage de la sortie suivante −
l = -1 r = 1
MATLAB



