MATLAB - Différentiel
MATLAB fournit le diff commande pour calculer les dérivées symboliques. Dans sa forme la plus simple, vous transmettez la fonction que vous souhaitez différencier à la commande diff en tant qu'argument.
Par exemple, calculons la dérivée de la fonction f(t) =3t 2 + 2t -2
Exemple
Créez un fichier de script et tapez-y le code suivant −
syms t f = 3*t^2 + 2*t^(-2); diff(f)
Lorsque le code ci-dessus est compilé et exécuté, il produit le résultat suivant −
ans = 6*t - 4/t^3
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
Octave exécute le code et renvoie le résultat suivant −
ans = -(4.0)*t^(-3.0)+(6.0)*t
Vérification des règles élémentaires de différenciation
Énonçons brièvement diverses équations ou règles de différenciation des fonctions et vérifions ces règles. Pour cela, on notera f'(x) pour une dérivée du premier ordre et f"(x) pour une dérivée du second ordre.
Voici les règles de différenciation −
Règle 1
Pour toute fonction f et g et tout nombre réel a et b sont la dérivée de la fonction −
h(x) =af(x) + bg(x) par rapport à x est donnée par −
h'(x) =af'(x) + bg'(x)
Règle 2
La somme et soustraction les règles stipulent que si f et g sont deux fonctions, f' et g' sont respectivement leurs dérivées, alors,
(f + g)' =f' + g'
(f - g)' =f' - g'
Règle 3
Le produit la règle stipule que si f et g sont deux fonctions, f' et g' sont respectivement leurs dérivées, alors,
(f.g)' =f'.g + g'.f
Règle 4
Le quotient la règle stipule que si f et g sont deux fonctions, f' et g' sont respectivement leurs dérivées, alors,
(f/g)' =(f'.g - g'.f)/g 2
Règle 5
Le polynôme ou la règle de puissance élémentaire stipule que, si y =f(x) =x n , alors f' =n. x (n-1)
Un résultat direct de cette règle est que la dérivée de toute constante est nulle, c'est-à-dire si y =k , toute constante, alors
f' =0
Règle 6
La chaîne règle stipule que, dérivée de la fonction d'une fonction h(x) =f(g(x)) par rapport à x est,
h'(x)=f'(g(x)).g'(x)
Exemple
Créez un fichier de script et tapez-y le code suivant −
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
Lorsque vous exécutez le fichier, MATLAB affiche le résultat suivant −
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
Octave exécute le code et renvoie le résultat suivant −
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
Dérivées des fonctions exponentielles, logarithmiques et trigonométriques
Le tableau suivant fournit les dérivées des fonctions exponentielles, logarithmiques et trigonométriques couramment utilisées −
| Fonction | Dérivé |
|---|---|
| c a.x | c a.x .ln c.a (ln est le logarithme népérien) |
| e x | e x |
| ln x | 1/x |
| lnc x | 1/x.ln c |
| x x | x x .(1 + ln x) |
| péché(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | s 2 (x), ou 1/cos 2 (x), ou 1 + tan 2 (x) |
| lit(x) | -csc 2 (x), ou -1/sin 2 (x), ou -(1 + lit 2 (x)) |
| sec(x) | sec(x).tan(x) |
| csc(x) | -csc(x).cot(x) |
Exemple
Créez un fichier de script et tapez-y le code suivant −
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
Lorsque vous exécutez le fichier, MATLAB affiche le résultat suivant −
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
Octave exécute le code et renvoie le résultat suivant −
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
Calcul des dérivées d'ordre supérieur
Pour calculer les dérivées supérieures d'une fonction f, on utilise la syntaxe diff(f,n) .
Calculons la dérivée seconde de la fonction y =f(x) =x .e -3x
f = x*exp(-3*x); diff(f, 2)
MATLAB exécute le code et renvoie le résultat suivant −
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
Octave exécute le code et renvoie le résultat suivant −
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
Exemple
Dans cet exemple, résolvons un problème. Sachant qu'une fonction y =f(x) =3 sin(x) + 7 cos(5x) . Nous devrons découvrir si l'équation f" + f =-5cos(2x) est vrai.
Créez un fichier de script et tapez-y le code suivant −
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Lorsque vous exécutez le fichier, il affiche le résultat suivant −
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Octave exécute le code et renvoie le résultat suivant −
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
Rechercher les maxima et les minima d'une courbe
Si nous recherchons les maxima et minima locaux pour un graphique, nous recherchons essentiellement les points les plus élevés ou les plus bas sur le graphique de la fonction à une localité particulière, ou pour une plage particulière de valeurs de la variable symbolique.
Pour une fonction y =f(x) les points sur le graphique où le graphique a une pente nulle sont appelés points stationnaires . En d'autres termes, les points stationnaires sont où f'(x) =0.
Pour trouver les points stationnaires d'une fonction que nous différencions, nous devons définir la dérivée égale à zéro et résoudre l'équation.
Exemple
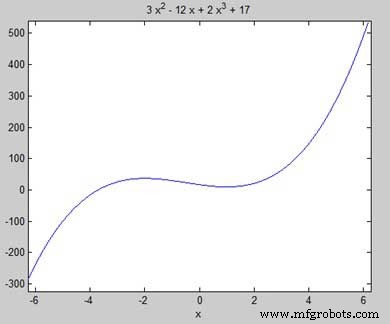
Trouvons les points stationnaires de la fonction f(x) =2x 3 + 3x 2 − 12x + 17
Suivez les étapes suivantes −
Entrons d'abord dans la fonction et traçons son graphique.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB exécute le code et renvoie le tracé suivant −
Voici le code équivalent Octave pour l'exemple ci-dessus −
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
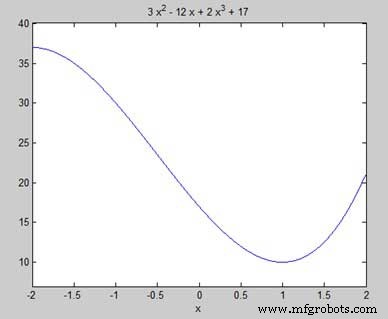
Notre objectif est de trouver des maxima et minima locaux sur le graphique, alors trouvons les maxima et minima locaux pour l'intervalle [-2, 2] sur le graphique.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB exécute le code et renvoie le tracé suivant −
Voici le code équivalent Octave pour l'exemple ci-dessus −
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
Ensuite, calculons la dérivée.
g = diff(y)
MATLAB exécute le code et renvoie le résultat suivant −
g = 6*x^2 + 6*x - 12
Voici l'octave équivalent du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
Octave exécute le code et renvoie le résultat suivant −
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
Résolvons la fonction dérivée, g, pour obtenir les valeurs où elle devient nulle.
s = solve(g)
MATLAB exécute le code et renvoie le résultat suivant −
s = 1 -2
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
Octave exécute le code et renvoie le résultat suivant −
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
Cela correspond à notre intrigue. Évaluons donc la fonction f aux points critiques x =1, -2. Nous pouvons substituer une valeur dans une fonction symbolique en utilisant le subs commande.
subs(y, 1), subs(y, -2)
MATLAB exécute le code et renvoie le résultat suivant −
ans = 10 ans = 37
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
Par conséquent, les valeurs minimale et maximale de la fonction f(x) =2x 3 + 3x 2 − 12x + 17, dans l'intervalle [-2,2] sont 10 et 37.
Résoudre des équations différentielles
MATLAB fournit le dsolve commande pour résoudre symboliquement les équations différentielles.
La forme la plus basique de dsolve commande pour trouver la solution à une seule équation est
dsolve('eqn')
où eqn est une chaîne de texte utilisée pour saisir l'équation.
Il renvoie une solution symbolique avec un ensemble de constantes arbitraires que MATLAB étiquette C1, C2, etc.
Vous pouvez également spécifier les conditions initiales et aux limites du problème, sous forme de liste délimitée par des virgules après l'équation sous la forme −
dsolve('eqn','cond1', 'cond2',…)
Aux fins de l'utilisation de la commande dsolve, les dérivés sont indiqués par un D . Par exemple, une équation telle que f'(t) =-2*f + cost(t) est saisie sous la forme −
'Df =-2*f + cos(t)'
Les dérivées supérieures sont indiquées en faisant suivre D de l'ordre de la dérivée.
Par exemple, l'équation f"(x) + 2f'(x) =5sin3x doit être saisie sous la forme −
'D2y + 2Dy =5*sin(3*x)'
Prenons un exemple simple d'équation différentielle du premier ordre :y' =5y.
s = dsolve('Dy = 5*y')
MATLAB exécute le code et renvoie le résultat suivant −
s = C2*exp(5*t)
Prenons un autre exemple d'équation différentielle du second ordre comme :y" - y =0, y(0) =-1, y'(0) =2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB exécute le code et renvoie le résultat suivant −
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB



