MATLAB - Intégration
L'intégration traite deux types de problèmes essentiellement différents.
-
Dans le premier type, la dérivée d'une fonction est donnée et nous voulons trouver la fonction. Par conséquent, nous renversons fondamentalement le processus de différenciation. Ce processus inverse est connu sous le nom d'anti-différenciation, ou recherche de la fonction primitive, ou recherche d'une intégrale indéfinie .
-
Le deuxième type de problèmes consiste à additionner un très grand nombre de très petites quantités puis à prendre une limite lorsque la taille des quantités tend vers zéro, tandis que le nombre de termes tend vers l'infini. Ce processus conduit à la définition de l'intégrale définie .
Les intégrales définies sont utilisées pour trouver l'aire, le volume, le centre de gravité, le moment d'inertie, le travail effectué par une force et dans de nombreuses autres applications.
Rechercher une intégrale indéfinie avec MATLAB
Par définition, si la dérivée d'une fonction f(x) est f'(x), alors on dit qu'une intégrale indéfinie de f'(x) par rapport à x est f(x). Par exemple, puisque la dérivée (par rapport à x) de x 2 est 2x, on peut dire qu'une intégrale indéfinie de 2x est x 2 .
En symboles −
f'(x 2 ) =2x , donc,
∫ 2xdx =x 2 .
L'intégrale indéfinie n'est pas unique, car la dérivée de x 2 + c, pour toute valeur d'une constante c, sera également 2x.
Ceci est exprimé en symboles comme −
∫ 2xdx =x 2 + c .
Où, c est appelé une "constante arbitraire".
MATLAB fournit un int commande pour calculer l'intégrale d'une expression. Pour dériver une expression de l'intégrale indéfinie d'une fonction, on écrit −
int(f);
Par exemple, de notre exemple précédent −
syms x int(2*x)
MATLAB exécute l'instruction ci-dessus et renvoie le résultat suivant −
ans = x^2
Exemple 1
Dans cet exemple, trouvons l'intégrale de certaines expressions couramment utilisées. Créez un fichier de script et tapez-y le code suivant −
syms x n int(sym(x^n)) f = 'sin(n*t)' int(sym(f)) syms a t int(a*cos(pi*t)) int(a^x)
Lorsque vous exécutez le fichier, il affiche le résultat suivant −
ans = piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)]) f = sin(n*t) ans = -cos(n*t)/n ans = (a*sin(pi*t))/pi ans = a^x/log(a)
Exemple 2
Créez un fichier de script et tapez-y le code suivant −
syms x n int(cos(x)) int(exp(x)) int(log(x)) int(x^-1) int(x^5*cos(5*x)) pretty(int(x^5*cos(5*x))) int(x^-5) int(sec(x)^2) pretty(int(1 - 10*x + 9 * x^2)) int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2) pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))
Notez que le joli La fonction renvoie une expression dans un format plus lisible.
Lorsque vous exécutez le fichier, il affiche le résultat suivant −
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2
Rechercher une intégrale définie à l'aide de MATLAB
Par définition, l'intégrale définie est fondamentalement la limite d'une somme. Nous utilisons des intégrales définies pour trouver des zones telles que la zone entre une courbe et l'axe des x et la zone entre deux courbes. Les intégrales définies peuvent également être utilisées dans d'autres situations, où la quantité requise peut être exprimée comme la limite d'une somme.
Le entier La fonction peut être utilisée pour une intégration définie en passant les limites sur lesquelles vous voulez calculer l'intégrale.
Pour calculer
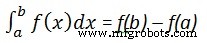
nous écrivons,
int(x, a, b)
Par exemple, pour calculer la valeur de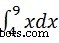 
nous écrivons −
int(x, 4, 9)
MATLAB exécute l'instruction ci-dessus et renvoie le résultat suivant −
ans = 65/2
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));
Octave exécute le code et renvoie le résultat suivant −
Area: 32.500
Une solution alternative peut être donnée en utilisant la fonction quad() fournie par Octave comme suit −
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));
Octave exécute le code et renvoie le résultat suivant −
Area: 32.500
Exemple 1
Calculons l'aire comprise entre l'axe des abscisses et la courbe y =x 3 −2x+5 et les ordonnées x =1 et x =2.
La surface requise est donnée par −
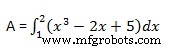
Créez un fichier de script et tapez le code suivant −
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));
Lorsque vous exécutez le fichier, il affiche le résultat suivant −
a = 23/4 Area: 5.7500
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));
Octave exécute le code et renvoie le résultat suivant −
Area: 5.7500
Une solution alternative peut être donnée en utilisant la fonction quad() fournie par Octave comme suit −
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));
Octave exécute le code et renvoie le résultat suivant −
Area: 5.7500
Exemple 2
Trouvez l'aire sous la courbe :f(x) =x 2 cos(x) pour −4 ≤ x ≤ 9.
Créez un fichier de script et écrivez le code suivant −
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));
Lorsque vous exécutez le fichier, MATLAB trace le graphique −
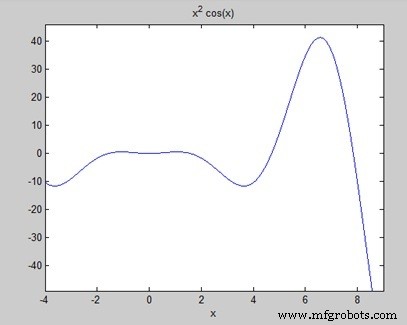
La sortie est donnée ci-dessous −
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326
Voici l'équivalent Octave du calcul ci-dessus −
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));
MATLAB