Transition de bande interdite indirecte-directe-indirecte contrôlée par champ électrique en monocouche InSe

Introduction

Depuis les travaux pionniers sur la réalisation expérimentale d'un graphite monocouche, à savoir le graphène [1, 2], les matériaux bidimensionnels (2D) atomiquement minces ont fait l'objet de beaucoup d'attention [3, 4]. Divers matériaux 2D monocouches ont été théoriquement prédits ou découverts expérimentalement, notamment le silicène [5-7], le germanane [8], le phosphore noir [9, 10], les dichalcogénures de métaux de transition (TMD) [11-13] et le nitrure de bore hexagonal [14 –16]. Bien que ces matériaux 2D atomiquement minces aient des structures de réseau en nid d'abeille similaires, leurs structures électroniques et leurs propriétés de conductivité sont assez différentes, notamment le métal [1, 2, 5–8], le semi-conducteur [9–13] et l'isolant [14–16]. Par conséquent, selon leurs caractères électroniques, ces matériaux 2D monocouches peuvent trouver des applications dans la conception de dispositifs électroniques et optiques multifonctionnels [3, 4]. Par exemple, des dispositifs optiques accordables avec un facteur de haute qualité basés sur des métamatériaux Si-graphène [17], des métamatériaux Cu-graphène [18] et MoS₂ -SiO₂ Des structures de guide d'onde -Si [19] sont proposées. Des dispositifs de polarisation de vallée parfaite ou/et de spin basés sur le graphène ferromagnétique [20], le graphène contraint avec couplage spin-orbite Rashba et barrière magnétique [21] et le silicène contraint avec un champ électrique sont suggérés [22, 23]. De plus, les effets d'interaction entre les composantes de décomposition de SF₆ et différents matériaux dont les nanotubes de carbone monoparoi dopés N [24], Pt₃ -TiO₂ (1 0 1) surface [25], MoS dopé Ni₂ monocouche [26] et la surface Pd (1 1 1) [27] sont étudiées en utilisant la théorie de la fonctionnelle de la densité (DFT).

Les composés MX des groupes III-VI (M =Ga, In et X =S, Se, Te) sont une autre famille de matériaux 2D en couches. En raison de leurs caractéristiques électriques uniques, ces matériaux ont attiré l'attention de nombreux chercheurs [28]. Les calculs DFT [29-33] et du modèle à liaison étroite [34] montrent que la bande interdite énergétique des MX en couches dépend de l'épaisseur, augmentant de 1,3 à 3,0 eV à mesure que le nombre de couches diminue. Dans le même temps, une transition de bande interdite directe-indirecte est observée, ce qui est opposé aux comportements du phosphore noir en couches [9, 10] et des TMD [11-13]. Cette importante modulation de bande interdite d'énergie des MX en couches peut être utilisée pour concevoir des dispositifs optoélectroniques [35, 36]. De plus, la stabilité de l'InSe dopé avec des défauts d'oxygène est étudiée et trouve qu'il est plus stable que le phosphore noir dans l'air [37]. Le magnétisme de la monocouche d'InSe peut être ajusté en adsorbant As [38], C et F [39]. Un énorme effet de conversion de charge de spin est trouvé dans la bicouche InSe en raison de la symétrie du miroir brisé [40]. De plus, la structure électronique et les caractéristiques courant-tension des nanorubans d'InSe monocouche dépendent fortement des états de bord [41]. D'autre part, des recherches expérimentales vérifient les structures électroniques dépendantes des couches des MX et elles peuvent répondre à la lumière couvrant les régions visible et proche infrarouge [42-45]. De plus, les mobilités des porteurs des MX s'avèrent élevées, ce qui permet de les utiliser pour concevoir des transistors à effet de champ. Pour le GaS et le GaSe en vrac, les mobilités des porteurs sont d'environ 80 et 215 cm ² V ⁻¹ S ⁻¹ [46], respectivement. Pour l'InSe monocouche, la mobilité des porteurs est même jusqu'à près de 10 ³ cm ² V ⁻¹ S ⁻¹ [47]. De plus, la bande interdite de l'InSe en couches peut être manipulée par une contrainte de traction uniaxiale, qui est identifiée par les spectres de photoluminescence [48].

Du point de vue de la conception de dispositifs optoélectroniques, l'efficacité des dispositifs basés sur des semi-conducteurs à bande interdite directe est meilleure que celle basée sur des semi-conducteurs à bande interdite indirecte. Par conséquent, transformer les MX à quelques couches à bande interdite indirecte en un type à bande interdite directe est un défi pour la communauté scientifique. Très récemment, la manipulation de bande interdite et la transition de bande interdite indirecte-directe ont été trouvées dans l'InSe monocouche par déformation uniaxiale [49]. De plus, des semi-conducteurs à bande interdite directe ont été obtenus en empilant du n-InSe et du p-GeSe(SnS) 2D. Et les valeurs de bande interdite et le décalage de bande de ces hétérojonctions de van der Waals peuvent être ajustés par le couplage intercouche et le champ électrique externe [50]. De plus, les configurations d'empilement possibles des bicouches InSe et l'influence du champ électrique perpendiculaire sur leurs structures électroniques sont étudiées. La bicouche à bande interdite indirecte InSe peut être transformée en type métallique en faisant varier l'intensité du champ électrique [51]. De même, dans d'autres matériaux 2D bouclés comme le silicène [52], le germanène [53], les dichalcogénures de métaux de transition [54, 55] et le phosphore noir [56], un champ électrique perpendiculaire est également proposé pour régler leur bande interdite et leurs caractéristiques électroniques. A la lumière de ces études précédentes, une question naturelle peut être posée quels sont les effets du champ électrique sur les structures électroniques de la monocouche InSe.

Dans cette lettre, les effets d'un champ électrique perpendiculaire sur les structures électroniques de la monocouche InSe sont étudiés en utilisant le modèle hamiltonien à liaison étroite. La transition de bande interdite indirecte-directe-indirecte peut être réalisée dans le système considéré avec une intensité de champ électrique croissante. Dans le même temps, la bande interdite de la monocouche InSe diminue progressivement, la rendant finalement métallique. Les mécanismes physiques sous-jacents de ces effets sont dévoilés en analysant la décomposition orbitale de la bande d'énergie et le décalage de position d'énergie modulé par le champ électrique des bords de la bande. Nos études peuvent être utiles pour comprendre fondamentalement les propriétés électroniques de l'InSe à quelques couches et fournir des bases théoriques pour les dispositifs optoélectroniques 2D.

Méthodes

La vue de dessus de la monocouche d'InSe est esquissée sur la figure 1a, où les grandes sphères violettes représentent les ions indium tandis que les petites vertes représentent les ions sélénium. Ces deux types d'ions forment une structure hexagonale semblable au graphène dans le xy plan avec une constante de réseau a , la distance entre les ions In ou Se les plus proches. La figure 1b montre le schéma de la vue latérale de la monocouche d'InSe. A la différence du graphène, deux sous-couches à symétrie miroir dans le xz plan sont observés. La distance verticale entre les ions In (Se) des différentes sous-couches est fixée à d (D ). Par conséquent, une maille élémentaire d'InSe monocouche est constituée de quatre ions S e ₁ , Je n ₁ , S e ₂ , et Je n ₂ , comme le montre l'ellipse rouge sur la figure 1b, dans laquelle le numéro 1 (2) indique l'indice de la sous-couche.

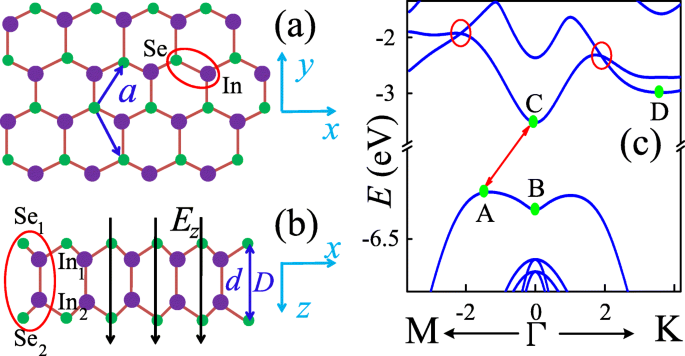
(Couleur en ligne) Haut (a ) et côté (b ) vue de la monocouche InSe dans le xy et xz avions, respectivement. La constante de réseau entre les ions In ou Se les plus proches dans le xy l'avion est un , et la distance entre les ions In (Se) les plus proches dans différentes sous-couches est d (D ). Un champ électrique perpendiculaire le long de z -axe E _z est appliqué à la monocouche InSe. c Bande d'énergie de l'InSe monocouche

L'hamiltonien à liaison étroite jusqu'aux interactions du deuxième voisin le plus proche, y compris tous les sauts possibles entre les s et p orbitales des ions In et Se se lit [34]

dans laquelle la somme passe sur les sous-couches l =1 et 2, et l ^′ =2(1) comme l =1(2). H _0l , H _je , et \(\phantom {\dot {i}\!}H_{ll^{\prime }}\) se composent de termes provenant des énergies sur site, sautant des énergies à l'intérieur et entre les deux sous-couches, respectivement. Et leurs expressions explicites sont données par [34]

où la somme s'étend sur toutes les cellules unitaires de la sous-couche l . \(\phantom {\dot {i}\!}\varepsilon _{\mathrm {In(Se)}_{s}}\) est l'énergie sur site pour les s orbitale des ions In (Se), tandis que \(\phantom {\dot {i}\!}\varepsilon _{\mathrm {In(Se)}_{p_{\alpha }}}\) est celle de l'orbitale p _α (α =x ,y ,z ). \(a_{lis}^{\dag }\) (a _lis ) est l'opérateur de création (annihilation) pour un électron dans s orbital sur In ions dans la maille élémentaire i et sous-couche l , mais \(\phantom {\dot {i}\!}a_{{lip}_{\alpha }}^{\dag }\) (\(\phantom {\dot {i}\!}a_{{ lip}_{\alpha }}\)) pour un électron dans p _α orbital. De même, b ^† (b ) est l'opérateur de création (annihilation) pour un électron dans l'orbitale pertinente sur les ions Se.

dans laquelle [34]

et

inclure les termes de saut entre les paires In-Se, In-In, Se-Se et In-Se les plus proches au sein de la même sous-couche l , respectivement. \(T_{ss/sp/ps}^{\mathrm {X}}\) est l'intégrale de saut pour le ss /sp /ps orbitales entre la paire correspondante X, tandis que \(T_{\pi (\sigma)}^{\mathrm {X}}\) est celle du parallèle p et p orbitales perpendiculaires au (se trouvant le long) du vecteur de saut \(R_{\alpha }^{\mathrm {X}}\) [57]. Par exemple

où \(\phantom {\dot {i}\!}\mathrm {\mathbf {R}}_{{\text {In}_{li}}/{\text {Se}_{lj}}}\ ) est le vecteur de position pour In_li /Se_lj , \(\hat {\mathbf {\alpha }}\) est un vecteur unitaire le long de α .

dans laquelle [34]

et

inclure les termes de saut entre les paires In-In, In-Se et In-In les plus proches voisines entre les sous-couches l et l ^′ , respectivement. Si un champ électrique perpendiculaire le long de z -axe est appliqué à la monocouche InSe, ses effets peuvent être introduits par une modification des énergies orbitales sur site des ions In et Se, c'est-à-dire

où e est la charge électronique et E _z est la force du champ électrique perpendiculaire. Le champ électrique perpendiculaire peut être obtenu en ajoutant des grilles supérieure et inférieure à la monocouche InSe. De plus, deux couches isolantes sont insérées entre la monocouche InSe et les grilles pour éliminer le courant électrique selon z -axe. En conséquence, l'intensité du champ électrique peut être réglée en faisant varier la tension de déclenchement.

En transformant l'hamiltonien à liaison étroite dans l'équation. (1) dans le k l'espace puis en le diagonalisant, les bandes d'énergie E (k ) d'InSe monocouche sans ou avec un champ électrique perpendiculaire peut être obtenu commodément, où k est un vecteur d'onde. En même temps, le coefficient du vecteur propre C _{n k} (o ) à la bande n , orbitale o , et vecteur d'onde k peut également être atteint.

Résultats numériques et discussions

Les paramètres de maille de la monocouche InSe dans les Fig. 1a et b sont pris comme a =3,953 Å, d =2,741 , et D =5,298 Å, qui sont obtenus par l'approximation de la densité locale [30]. Les énergies sur site et de saut dans l'équation hamiltonienne à liaison étroite. (1) sont donnés dans le tableau 1, qui sont ajustés par les données de la théorie fonctionnelle de la densité avec correction en ciseaux [34]. Bien que seuls les résultats numériques de l'InSe monocouche soient donnés ici, des résultats qualitativement similaires ont également été trouvés dans l'InSe bicouche et l'InSe massif. Par souci de concision, ils ne sont pas présentés dans cette lettre.

La figure 1c montre la bande d'énergie de la monocouche InSe. Les bandes de conduction autour du point Γ présentent une dispersion d'énergie semblable à une parabole, qui est similaire à celle d'autres semi-conducteurs normaux. Cependant, la structure de bande suivant Γ−K est légèrement asymétrique avec celle suivant Γ−M. Et les deux bandes de conduction les plus basses se croisent le long de ces deux directions, comme indiqué par les cycles rouges. Contrairement aux bandes de conduction, la bande de valence la plus élevée est plate mais légèrement inversée autour du point Γ, formant une intéressante structure mexicaine en forme de chapeau. Par conséquent, l'InSe monocouche est un semi-conducteur à bande interdite indirecte, qui est assez différent de celui de l'InSe massif puisqu'il s'agit d'un semi-conducteur à bande interdite directe. L'écart énergétique de la monocouche InSe peut être obtenu par \(E_{\mathrm {g}}^{\text {id}}=E_{\mathrm {C}}-E_{\mathrm {A}}=2.715\) eV, qui est très agrandi en comparant avec celui de l'InSe massif \(E_{\mathrm {g}}^{\mathrm {d}}=1.27\) eV [34]. Cependant, les autres bandes de valence montrent une dispersion d'énergie normale de type parabole.

Afin de comprendre la bande d'énergie de la monocouche InSe montrée sur la figure 1c, la décomposition orbitale |C _{n k} (o )| ² pour la bande d'énergie est donnée sur la Fig. 2. Comme les deux sous-couches de la monocouche InSe est symétrique le long de z -axe, les ions dans différentes sous-couches ont les mêmes contributions orbitales à la bande d'énergie. Ici, les ions In et Se dans la sous-couche 2, comme le montre la figure 1b, sont pris comme exemples. Les panneaux supérieurs indiquent les contributions orbitales des ions In tandis que les panneaux inférieurs représentent celles des ions Se. L'épaisseur des lignes est proportionnelle à la contribution orbitale normalisée. On peut voir que la bande de conduction la plus basse autour du point Γ est apportée en premier lieu par p _z orbitale de l'ion Se puis s orbitale de l'ion In. La deuxième bande de conduction autour du point K provient principalement de p _x orbitale de l'ion In puis p _z orbitale de l'ion Se. Cependant, la bande de valence la plus élevée est principalement due à p _z orbitale de l'ion Se. Les autres bandes de valence résultent à la fois de p _x et p _y orbitales de l'ion Se. Ces résultats sont cohérents avec ceux obtenus par les calculs DFT [34].

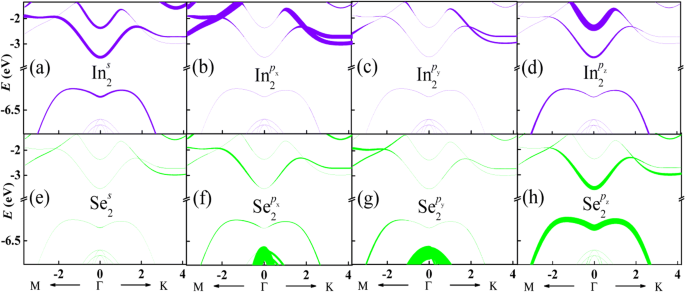
(Couleur en ligne) Décompositions orbitales pour la bande d'énergie de la monocouche InSe. Les lignes plus épaisses indiquent une contribution plus dominante. Seuls les ions In et Se de la sous-couche 2 sont choisis comme exemples puisque les deux sous-couches de la monocouche InSe à symétrie miroir le long de z -axe (a –h )

Bande d'énergie de la monocouche InSe avec un champ électrique perpendiculaire suivant z -axe est montré dans la Fig. 3a. L'intensité du champ électrique est prise comme E _z =2,0 V/nm. En comparant avec la bande d'énergie de la figure 1c, chaque bande de conduction et de valence est élevée dans la région d'énergie supérieure dans son ensemble. Cependant, le décalage énergétique de chaque bande est différent puisque sa décomposition orbitale à partir du p _z l'orbitale des ions In et Se est différente. La position de la valeur maximale de la bande de valence la plus élevée est modifiée au point tandis que celle de la valeur minimale de la bande de conduction reste inchangée. Par conséquent, la monocouche InSe est transformée en un semi-conducteur à bande interdite directe. Et l'écart énergétique est réduit à \(E_{\mathrm {g}}^{\mathrm {d}}=2.61\) eV. De plus, les croisements le long des deux directions Γ−K et Γ−M sont ouverts de sorte que des écarts d'énergie sont générés, comme indiqué par les cycles rouges, puisque la symétrie le long de z -axe est brisé par le champ électrique perpendiculaire. Lorsque l'intensité du champ électrique est augmentée à E _z =6,0 V/nm, l'écart énergétique au point Γ est diminué mais ceux aux croisements sont encore augmentés, comme le montre la figure 3b. Fait intéressant, la position de la valeur minimale de la bande de conduction est modifiée du point Γ à celle autour du point K, tandis que celle de la valeur maximale de la bande de valence la plus élevée reste au point Γ. Ce phénomène signifie que la monocouche InSe transite à nouveau dans le semi-conducteur à bande interdite indirecte et que la bande interdite indirecte de toute la bande \(E_{\mathrm {g}}^{\text {id}}=1.30\) eV. De même, la bande interdite de la monocouche InSe peut être contrôlée par déformation biaxiale. La bande interdite varie de 1,466 à 1,040 eV lorsque la contrainte varie de 1 à 4%. De plus, une transition de bande interdite indirecte-directe est également observée lorsque la monocouche InSe est sous contrainte uniaxiale [49]. Pour le bicouche InSe avec un champ électrique perpendiculaire, sa bande interdite diminue à mesure que l'intensité du champ électrique augmente et il se fermera lorsque l'intensité du champ électrique est augmentée à 2,9 V/nm [51].

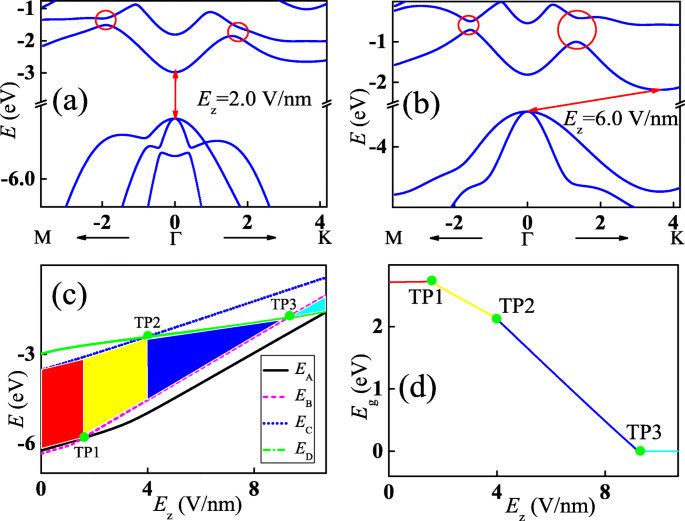
(Couleur en ligne) Bandes d'énergie de la monocouche modulée par champ électrique perpendiculaire InSe à différentes intensités E _z =2.0 V/nm(a ) et 6,0 V/nm (b ), respectivement. Cercles rouges dans a et b signifient les écarts d'énergie ouverts autour des points de croisement illustrés à la Fig. 1c. c Énergies aux points A (la ligne continue noire), B (la ligne pointillée magenta), C (la ligne pointillée bleue) et D (la ligne pointillée verte) illustrées à la Fig. 1c en fonction de l'intensité du champ électrique . d Bande interdite globale en fonction de l'intensité du champ électrique. La ligne jaune signifie la bande interdite directe tandis que les lignes rouges et bleues indiquent les bandes interdites indirectes

Pour mieux comprendre le processus changeant de la structure électronique de la monocouche InSe en présence d'un champ électrique perpendiculaire, les énergies aux vecteurs d'onde correspondant aux points A, B, C et D aux bords de la bande illustrés à la Fig. 1c en fonction de l'intensité du champ électrique sont représentés sur la figure 3c. Les énergies par rapport à tous ces points se déplacent vers le haut à mesure que l'intensité du champ électrique augmente, confirmant l'évolution des bandes d'énergie sur les Fig. 3a et b. Lorsque l'intensité du champ électrique E _z <1,6 V/nm, l'énergie au point A dans la bande de valence est supérieure à celle du point B tandis que le bas de la bande de conduction se situe au point C. Par conséquent, la monocouche modulée par champ électrique InSe dans cette plage d'intensité est une bande interdite indirecte semi-conducteur, comme indiqué par la zone rouge. Cependant, les énergies par rapport aux points A et B se croiseront à TP1, puis l'énergie au point B sera plus élevée que celle du point A à mesure que l'intensité du champ électrique augmente davantage. Simultanément, le bas de la bande de conduction reste inchangé jusqu'à ce que l'intensité du champ électrique soit augmentée à 4,0 V/nm. En conséquence, la monocouche InSe modulée par champ électrique dans cette plage de résistance est un semi-conducteur à bande interdite directe, comme indiqué par la zone jaune. Semblable au croisement d'énergie entre les points A et B dans la bande de valence, le point de transit est également observé dans les énergies aux points C et D dans les bandes de conduction, comme indiqué par TP2. L'énergie au point D est inférieure à celle du point C tandis que le haut de la bande de valence reste toujours au point B si seule l'intensité du champ électrique est inférieure à 9,23 V/nm. Par conséquent, la monocouche InSe modulée par champ électrique est à nouveau transformée en semi-conducteur à bande interdite indirecte, comme le montre la zone bleue. Fait intéressant, les énergies au point B dans la bande de valence la plus élevée et au point D dans la bande de conduction la plus basse se croiseront également à TP3, ce qui signifie que la bande interdite est fermée. De plus, l'énergie au point B sera supérieure à celle du point D lorsque l'intensité du champ électrique est supérieure à 9,23 V/nm. Par conséquent, la bande de conduction la plus basse et la bande de valence la plus élevée se chevaucheront de sorte que la monocouche modulée par champ électrique InSe devienne un métal dans ce cas, comme le montre la zone cyan. La bande interdite globale correspondant aux différentes zones colorées de la figure 3c est tracée sur la figure 3d. La bande interdite correspondant à la zone rouge est presque indépendante de l'intensité du champ électrique varié, comme indiqué par la ligne rouge. Cependant, la bande interdite de la zone jaune diminue linéairement avec l'augmentation de l'intensité du champ électrique. Un comportement de bande interdite similaire est également observé dans la zone bleue mais avec une pente plus importante. La bande interdite est réduite à zéro tant que l'intensité du champ électrique est supérieure à celle au point TP3, comme indiqué par la ligne cyan. Les comportements de bande interdite modulée par champ électrique indiquent que les semi-conducteurs en couches III-VI ont des applications potentielles dans la conception de nouveaux détecteurs et absorbeurs optiques. De plus, la fréquence de réponse spectrale de ces appareils varie en continu de la lumière violette (ν ≈6,57×10 ¹⁴ Hz comme Mi _z =1.6 V/nm) à la lumière infrarouge (ν <3.97×10 ¹⁴ Hz comme Mi _z >5.18 V/nm).

Comme on le sait, les caractéristiques électroniques des matériaux sont principalement déterminées par les bords des bandes d'énergie. D'après la décomposition orbitale de la bande d'énergie de la Fig. 2, les bords des bandes de conduction et de valence de la monocouche InSe sont principalement contribués par p _z orbitale de l'ion Se. Par conséquent, seul p _z les décompositions orbitales de l'ion Se dans la sous-couche 2 pour les bandes d'énergie montrées sur les Fig. 3a et b sont affichées sur les Fig. 4a et b, respectivement. En comparant avec la Fig. 2h, p _z la contribution orbitale aux bandes de conduction est légèrement modifiée. Par conséquent, la forme de ces structures de bande subit peu d'affection. Cependant, le p _z la contribution orbitale aux bandes de valence est fortement modifiée, entraînant le changement de forme de ces structures de bandes. De plus, selon le p _z décomposition orbitale pour la bande d'énergie de la monocouche InSe avec un champ électrique perpendiculaire, la position relative de chaque bande de conduction reste inchangée bien que des lacunes soient ouvertes aux croisements de bandes, comme indiqué par les cycles rouges. Au contraire, la position relative de chaque bande de valence est modifiée. Les énergies des bandes de valence inférieure autour de Γ points augmentent et dépassent finalement ceux de la bande de valence la plus élevée, conduisant à une transition de bande interdite indirecte-directe.

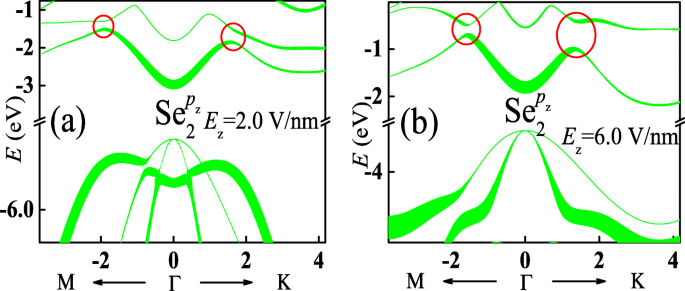
(Couleur en ligne) a et b afficher p _z décomposition orbitale de l'ion Se dans la sous-couche 2 pour les bandes d'énergie de la monocouche InSe avec un champ électrique perpendiculaire illustré sur les Fig. 3a et b, respectivement. Les lignes plus épaisses représentent une contribution plus importante

Conclusions

Les structures électroniques d'InSe monocouche sous la modulation d'un champ électrique perpendiculaire sont étudiées. Une transition de bande interdite indirecte-directe-indirecte est trouvée pour la monocouche InSe en ajustant l'intensité du champ électrique. Simultanément, la bande interdite globale de ce système est réduite de façon monotone à zéro avec l'augmentation de l'intensité du champ électrique, ce qui signifie que la transition semi-conducteur-métal est réalisée. L'évolution de la bande d'énergie de la monocouche InSe en présence du champ électrique perpendiculaire est clarifiée en analysant le changement d'énergie du bord de bande et la décomposition orbitale pour la bande d'énergie. Ces résultats peuvent être utiles pour mieux comprendre les structures électroniques de l'InSe monocouche ainsi que la conception de dispositifs photoélectriques à base d'InSe monocouche répondant de la lumière violette à l'infrarouge lointain.

Disponibilité des données et des matériaux

Les ensembles de données soutenant les conclusions de cet article sont inclus dans l'article.

Abréviations

2D :

Bidimensionnel

DFT :

Théorie fonctionnelle de la densité

TMD :

Dichalcogénures de métaux de transition