Effet de la morphologie et de la structure cristalline sur la conductivité thermique des nanotubes de titane

Contexte

En raison de la miniaturisation persistante des dispositifs électroniques et des systèmes nano-électro-mécaniques (NEMS), l'étude des nanostructures et de leurs propriétés a attiré beaucoup d'attention ces dernières années [1, 2]. Les études sur le contrôle de la taille et de la nucléation des nanostructures ont déjà été présentées, car les nanostructures ont été utilisées pour différentes applications potentielles [3, 4]. La recherche sur le contrôle des propriétés thermiques des nanostructures en contrôlant la taille, la composition et la structure est particulièrement intéressante en raison de leurs applications dans l'industrie électronique, NEMS et thermoélectrique avancé [2, 5, 6]. Un cas particulier consiste à minimiser la dissipation thermique dans les circuits intégrés (CI) pour leur stabilité et leur longue durée de vie.

Les matériaux unidimensionnels (1D), tels que les nanotubes de carbone (CNT), possèdent une conductivité thermique à température ambiante de 3 000 W m ⁻¹ K ⁻¹ , ce qui est bien supérieur à celui d'un cristal de diamant [2, 5]. Le CNT est une feuille de graphène laminée sans soudure et a une conductivité thermique plus élevée en raison de la forte liaison carbone-carbone et de l'absence de défauts et de limites ponctuels [6]. Contrairement au CNT, d'autres semi-conducteurs cristallins unidimensionnels ont un transport thermique considérablement réduit par rapport au matériau en vrac [6]. Cette diminution de la conductivité thermique dans les nanostructures de faible dimension est attribuée à la réduction du libre parcours moyen (MFP) des phonons, de la petite taille des grains, de la diffusion aux limites des phonons, de la rugosité et des défauts ponctuels [6,7,8].

Les nanofils de silicium ont été étudiés pour adapter le transport thermique à leur utilisation dans des applications thermoélectriques. Pour la première fois, Li et al. [9] ont rapporté des conductivités thermiques deux fois inférieures pour les nanofils de silicium par rapport au silicium massif en raison de la diffusion aux limites des phonons. La conductivité thermique des nanofils de silicium d'un diamètre de 50 nm approchait de la limite amorphe du silicium, avec une réduction de 100 fois de la conductivité thermique par rapport au silicium massif [10]. Ces nanofils de silicium avec une conductivité thermique considérablement réduite et une conductivité électrique accrue possèdent une efficacité thermoélectrique plus élevée [10,11,12,13]. Les propriétés thermiques réduites d'autres nanofils par rapport à leurs matériaux en vrac sont également signalées, telles que Bi₂ Te₃ [14, 15], Si/SiGe [16], Ge/SiGe [17, 18], ZnTe [19], GaN [20], InSb [21], CdS [22], PbS, PbSe [23], InAs [24], Bi [25], SrTiO₃ [26], ZnO [27] et TiO₂ nanofils [28, 29]. De plus, les études thermiques sur les nanotubes tels que Si [30], Bi₂ Te₃ [31], et TiO₂ des nanotubes [1, 32, 33, 34] ont été rapportés. Sur la base de ces études, on peut conclure que la conductivité thermique des nanotubes est inférieure à celle des nanofils correspondants en raison de la diffusion supplémentaire de phonons à l'intérieur des parois des nanotubes [31]. Il est à noter que la conductivité thermique des nanotubes cristallins est généralement plus élevée que celle de leurs homologues amorphes et fortement influencée par leur rugosité de surface [32, 34]. De plus, Wingert et al. [30] ont remarqué que les nanotubes de silicium cristallin ont une conductivité thermique inférieure à leurs équivalents amorphes. Cette observation de conductivité thermique au-delà de la limite amorphe dans les nanotubes de silicium cristallin a été attribuée à un ramollissement élastique et à une forte diffusion aux limites des phonons [30]. Le transport thermique dans les nanomatériaux amorphes est principalement (93 %) attribué aux diffusons (modes « diffusion » non propagés), tandis que les 4 % restants sont liés aux modes de type phonon appelés « propagones » et 3 % aux modes localisés. connu sous le nom de « locons » [35]. Puisque le libre parcours moyen des diffusons est généralement considéré comme celui de la distance interatomique, on s'attend à ce que la conductivité thermique des nanostructures amorphes soit indépendante des dimensions [36].

Cahill et Pohl ont proposé un modèle de conductivité thermique minimum bien connu pour les matériaux désordonnés [37]. Selon ce modèle, la conductivité thermique minimale proposée (limite amorphe) de l'oxyde de titane est de 1,6 W m ⁻¹ K ⁻¹ [38]. Aucune réduction dépendante de la taille de la conductivité thermique des oxydes amorphes n'a été rapportée [35] bien que certains films d'oxydes aient été revendiqués comme ayant une conductivité thermique inférieure à la limite amorphe. La raison de la valeur inférieure de la conductivité thermique obtenue a été attribuée aux impuretés dans la structure ou, dans le cas des films minces, à la résistance thermique à la limite entre le film et le substrat [35].

Les nanotubes de titane, nanostructures 1D à surface spécifique élevée, ont été conçus pour un certain nombre d'applications potentielles [39]. Les nanotubes de titane peuvent être synthétisés par diverses méthodes, notamment l'anodisation hydrothermale [40] et électrochimique [39, 40], le traitement chimique [41], l'anodisation par claquage rapide (RBA) [42] et les méthodes assistées par gabarit et par électrofilage [40]. Conductivité thermique comprise entre 0,40 et 0,84 W m ⁻¹ K ⁻¹ [1] et 0,55-0,75 W m ⁻¹ K ⁻¹ [33] ont été observés pour des nanotubes de titanate synthétisés par procédé hydrothermal. Brahmi et al. [32] ont signalé une conductivité thermique de 0,85 W m ⁻¹ K ⁻¹ pour un seul nanotube amorphe et 1,5 W m ⁻¹ K ⁻¹ pour le nanotube d'oxyde de titane anatase préparé par anodisation électrochimique. D'autre part, les réseaux de nanotubes de titane détachés auraient une conductivité thermique de 0,617 W m ⁻¹ K ⁻¹ le long de la direction du tube pour amorphe et 1,12 W m ⁻¹ K ⁻¹ pour les nanotubes anatase [34]. La conductivité thermique amorphe du tube croisé était de 0,077-0,1024 W m ⁻¹ K ⁻¹ pour les nanotubes amorphes et 0,24 W m ⁻¹ K ⁻¹ dans le cas des nanotubes cristallins [34]. Les réseaux de nanotubes de titane dans ces rapports sont cultivés sur un substrat de Ti par une méthode d'anodisation électrochimique utilisant des électrolytes organiques avec des ions fluorure (troisième génération de TNT) avec une épaisseur de paroi de 30 à 70 nm [32] et 15 nm [34]. Les nanotubes préparés par RBA comprennent la quatrième génération de TNT [43], où des faisceaux de nanotubes de titane sont obtenus en utilisant un électrolyte sans fluor [42].

Dans la présente contribution, nous rapportons une étude expérimentale comparative sur la conductivité thermique des nanotubes de dioxyde de titane avec une morphologie variable, une structure cristalline et une épaisseur de paroi inférieure à 30 nm. Les nanotubes sont synthétisés par traitement chimique [41] et RBA [42]. La recherche de conductivité thermique est étendue à la quatrième génération de nanotubes de dioxyde de titane (c'est-à-dire des poudres préparées par RBA) et à la comparaison de poudres de TNT par différentes méthodes de synthèse. Liang et Li [44] ont proposé un modèle analytique de conductivité thermique dépendant de la taille pour les nanomatériaux, qui a été confirmé expérimentalement pour les nanofils et les films. Le modèle a ensuite été modifié par Gao et Jelle [1] pour les nanotubes mais n'a pas été vérifié expérimentalement. Selon le modèle, la conductivité thermique des nanotubes dépend de l'épaisseur de paroi [1]. Brahmi et al. [32] ont étudié la conductivité thermique de TNT avec une épaisseur de paroi variable de 30 à 70 nm ; cependant, la réduction de la conductivité thermique avec l'épaisseur de la paroi n'a pas été observée dans leur étude. Dans le présent rapport, nous vérifions expérimentalement la conductivité thermique dépendant de la taille des nanotubes d'oxyde de titane en réduisant les dimensions de la paroi dans les nanotubes d'oxyde de titane cristallins. Contrairement à la perception générale, les données actuelles combinées à celles présentées dans la littérature suggèrent une réduction de la conductivité thermique en fonction de la taille également pour les nanotubes d'oxyde de titane amorphe.

Méthodes/Expérimental

Synthèse de TNT

Des poudres de nanotubes de titane (TNT) ont été préparées en utilisant des méthodes de traitement chimique et d'anodisation rapide (RBA) comme discuté en détail dans [41, 42], respectivement. Trois types de nanotubes d'oxyde de titane avec une structure cristalline et une morphologie différentes ont été préparés, à savoir (i) des TNT multiparois à extrémité ouverte, (ii) des TNT amorphes à paroi unique avec une extrémité ouverte et l'autre fermée, et (iii) des nanotubes d'oxyde de titane cristallins avec une extrémité ouverte et l'autre fermée. Les nanotubes de titane ouverts à parois multiples ont été préparés par une méthode de traitement chimique et avaient une structure cristalline mixte de titanate (Na_x H_2 − x Ti₃ O₇ ·nH₂ O, où 0 < x < 2) avec des pics proéminents de la phase anatase [41] et appelés TNT_A,T tout au long du texte. Deux autres types de nanotubes ont été préparés par la méthode RBA soit en utilisant un électrolyte à base d'eau (acide perchlorique 0,1 M) pour obtenir des TNT cristallins avec une structure anatase ou un électrolyte organique (éthylène glycol + eau + acide perchlorique) pour produire des nanotubes amorphes [42] . L'amorphe (TNT_Amor ) et cristallin (TNT_A ) Les poudres de nanotubes d'oxyde de titane produites par RBA sont à paroi simple avec une extrémité ouverte et l'autre fermée. L'illustration schématique de ces TNT est présentée sur la figure 1.

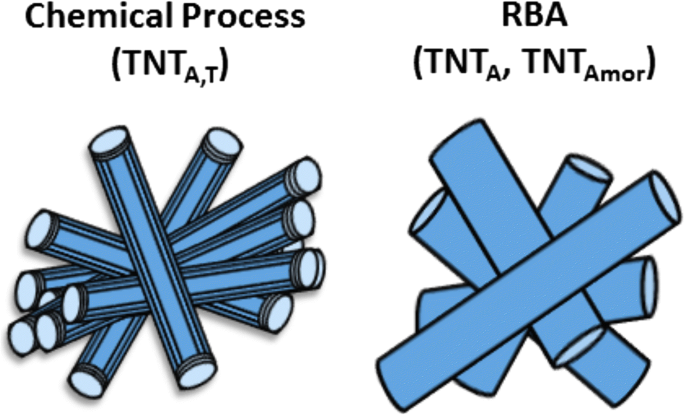
Illustration schématique de TNT_A,T , TNT_A , et TNT_Amor

Méthodes de caractérisation

La morphologie et la taille des poudres de nanotubes d'oxyde de titane ont été examinées par microscopie électronique à transmission (MET ; Tecnai F-20 G2 200 kV FEG S-twin GIF) à une tension de fonctionnement de 200 kV. La structure cristalline a été obtenue en utilisant la diffraction des rayons X (XRD). Les données XRD ont été obtenues en utilisant un diffractomètre PANalytical X'pert Pro. La longueur d'onde de fonctionnement était un rayonnement Cu-Kα de 0,154 nm, avec une tension et des courants de 40 kV et 45 mA, respectivement. La densité de chaque poudre a été mesurée par Pycnomètre (Upyc 1200e v5.04; Quantachrome Corporation). Les poudres ont ensuite été compressées en pastilles de 10 mm pour des mesures de conductivité thermique. Les pastilles ont été fabriquées par pressage hydrostatique de poudres de nanotubes et l'épaisseur des pastilles obtenues était de l'ordre de 2 à 4 mm. L'épaisseur mesurée et la densité calculée des pastilles sont liées à la pression appliquée, qui a été contrôlée sur une plage de 5 à 50 kN pour ajuster la densité de chaque pastille. Les surfaces des pastilles ont été analysées au microscope électronique à balayage par canon à émission de champ (FEG-SEM ; Hitachi S-4700).

La diffusivité thermique des pastilles a été mesurée en utilisant la méthode du flash lumineux en utilisant un équipement Netzsch LFA 467 avec le logiciel Proteus LFA à température ambiante. Une courte impulsion laser au xénon a chauffé la surface arrière des pastilles. Avant les mesures, les pastilles ont été enduites d'un spray de graphite pour améliorer l'absorption et l'émission du rayonnement thermique. Un détecteur infrarouge a observé le changement de température correspondant sur le côté opposé de la pastille. Selon Parker et al. [45], la relation suivante peut être utilisée pour obtenir la diffusivité thermique à partir des données expérimentales :

Ici, α est la diffusivité thermique de l'échantillon, d est l'épaisseur de l'échantillon, et t ^1/2 est la valeur temporelle à mi-hauteur du signal. Les mesures LFA ont été répétées cinq fois par échantillon. Le logiciel Proteus a été utilisé pour l'ajustement des mesures. La conductivité thermique de l'échantillon a été obtenue en utilisant la relation suivante [45] :

Ici, κ désigne la conductivité thermique, α désigne la diffusivité thermique, c _p est la capacité thermique spécifique, et ρ est la valeur de la densité. La capacité thermique spécifique des nanotubes de titane se rapproche de celle du dioxyde de titane en vrac au-dessus de 100 K [46], et par conséquent, les valeurs de la capacité thermique spécifique des nanotubes de titane ont été adoptées à partir d'une étude de Guo et al. [34, 47]. La densité des pastilles a été calculée à partir du poids et du volume correspondant des pastilles. L'incertitude sur les résultats expérimentaux provient des erreurs de l'unité de mesure LFA pour les mesures de diffusivité (2%) et le calcul de l'épaisseur des pastilles par un micromètre. L'erreur totale pour les expériences de conductivité thermique a été estimée à 8 %.

Résultats et discussion

Les données XRD pour la structure cristalline des nanotubes sont présentées sur la figure 2. Le TNT_Amor les données n'ont pas de pics confirmant la structure amorphe des nanotubes préparés par RBA en utilisant un électrolyte organique [42]. Les nanotubes traités chimiquement (TNT_A,T ) montrent des pics importants de la phase anatase avec H₂ Ti₃ O₇ pics. La structure autre que l'anatase a été assignée comme Na_x H_2 − x Ti₃ O₇ ·nH₂ O où 0 < x < 2, comme rapporté dans une étude précédente [41]. La TNT_A préparé par électrolyte à base d'eau ont des pics d'anatase. D'après les données XRD, il est évident que deux types de nanotubes sont cristallins et un est amorphe.

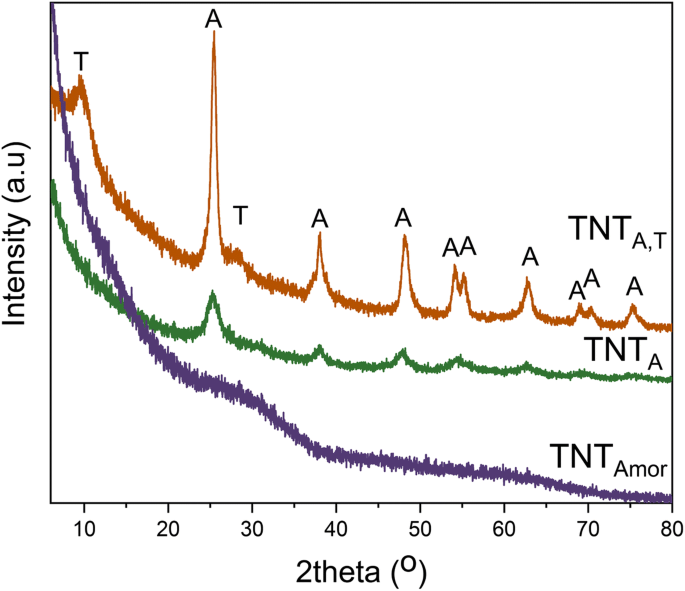
XRD de nanotubes d'oxyde de titane cristallins constitués d'anatase (TNT_A ), à la fois titanate et anatase (TNT_A,T ), et structure amorphe (TNT_Amor ) [41, 42]. T =H₂ Ti₃ O₇ , A =pics anatase

Les nanotubes de dioxyde de titane synthétisés par la méthode de traitement chimique sont multiparois en raison du défilement des nanofeuillets lors de la synthèse des nanotubes [48]. Ces nanotubes à extrémité ouverte ont une épaisseur de paroi de 4 à 5 nm avec une longueur variable de 60 à des centaines de nanomètres [41]. Les images MET de ces nanotubes sont présentées sur la figure 3a, b. Les nanotubes sont orientés de manière aléatoire et préfèrent rester en faisceaux comme le montre la figure 3a. La structure multiparois de 3 à 4 couches est évidente, comme le montre la figure 3b. Les nanotubes cristallins produits par RBA ont une épaisseur de paroi comprise entre 7 et 12 nm et mesurent 18 à 35 µm de long [42] (tableau 1). Ils sont à paroi simple avec une extrémité ouverte et l'autre fermée, comme le montre la micrographie de la Fig. 3c, où l'encart montre l'extrémité ouverte. Les nanotubes amorphes produits par RBA ont une morphologie similaire à celle des nanotubes cristallins préparés par la méthode RBA. Cependant, les dimensions sont différentes en raison de l'apport de l'électrolyte. L'épaisseur de la paroi est comprise entre 15 et 30 nm et la longueur tubulaire est comprise entre 6 et 13 μm [42]. La figure 3d montre l'image MET du nanotube amorphe à paroi unique. La rugosité est la valeur moyenne de l'écart de hauteur de la surface de la paroi en TNT par rapport au plan de référence [44]. Les valeurs de rugosité moyennes estimées à partir des images MET des TNT sont d'environ 0,3 nm pour le TNT_A,T , 1,0 nm pour TNT_A , et 1,5 nm pour la TNT_Amor .

Images TEM de a le TNT_A,T préparé par traitement chimique, b Micrographie HR-TEM montrant la structure de nanotubes multiparois, c les nanotubes cristallins monoparoi préparés (TNT_A ) par RBA, et d les nanotubes amorphes (TNT_Amor )

Les pastilles de nanotubes d'oxyde de titane ont été préparées en différentes densités et porosités correspondantes à l'aide d'une presse hydraulique. TNT_Amour la poudre a été compactée avec une charge maximale de 20 kN car à des charges plus élevées, la surface lisse des pastilles requise pour les mesures LFA n'a pas été obtenue. La porosité des pastilles est calculée par la formule suivante (Eq. 1) :

où ρ _o est la densité des échantillons en vrac, qui est la densité de la poudre obtenue par des mesures au pycnomètre et indiquée dans le tableau 1. Le ρ est la densité calculée de la pastille et P est la porosité des échantillons. Les surfaces des pastilles ont été étudiées avec FESEM dans le fichier supplémentaire 1. Les analyses des surfaces montrent une orientation aléatoire des faisceaux de nanotubes (fichier supplémentaire 1 :Figure S1) sur la surface, c'est-à-dire que les nanotubes peuvent être observés à différentes orientations (top ouvert, positions de vue inférieure et latérale fermées) dans le fichier supplémentaire 1 :Figure S1. Images SEM similaires de surfaces de pastilles de TNT_A , TNT_Amour , et TNT_A,T les granulés sont représentés dans le fichier supplémentaire 1 :Figure S2a–c. La diffusivité thermique mesurée par la méthode LFA est résumée dans le tableau 2. Les conductivités thermiques mesurées sont tracées en fonction de la porosité, comme indiqué sur la figure 4. La conductivité thermique mesurée diminue avec l'augmentation de la porosité pour tous les échantillons (tableau 2). Gao et Jelle ont obtenu une tendance similaire pour les valeurs de conductivité thermique d'échantillons avec différentes porosités de pastilles [1]. Une nette réduction de la conductivité thermique est obtenue pour les nanotubes par rapport à l'oxyde de titane massif (8,5 W m ⁻¹ K ⁻¹ [34]). Cette suppression de la conductivité thermique dans les nanotubes d'oxyde de titane 1D est attribuée au confinement des phonons et à la diffusion aux limites des phonons en raison de la réduction de la taille [1]. Comme les nanotubes sont orientés de manière aléatoire et compactés pour former des pastilles, ils sont également connectés les uns aux autres. Dans ce cas, la diffusion des phonons au niveau de la zone interconnectée entre les nanotubes et la résistance Kapitza affecte également les valeurs globales de conductivité thermique. Cependant, la résistance Kapitza de contact et la diffusion aux limites des phonons compte tenu de l'orientation des nanotubes sont ignorées ici pour des raisons de simplicité.

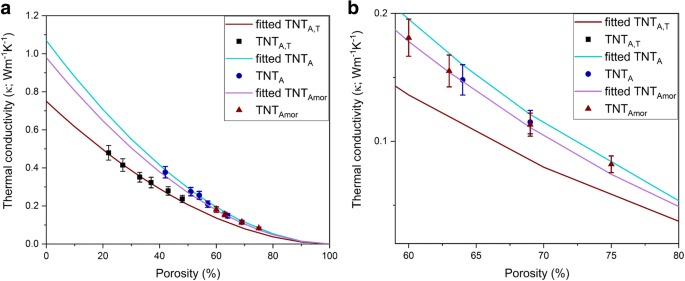
un Mesure de la conductivité thermique effective des nanotubes de dioxyde de titane (symboles) en fonction de la porosité. Les lignes pleines représentent l'ajustement à l'aide du modèle de conductivité thermique effective (Eq. 6) avec un facteur de forme de 1,24. b Conductivité thermique sur une plage de porosité de 60 à 80 % pour plus de clarté

La conductivité thermique mesurée d'un échantillon estime la conductivité des pastilles de nanotubes en considérant à la fois les nanotubes de dioxyde de titane et les pores remplis d'air. La conductivité thermique de l'air est présumée être de 0,026 W m ⁻¹ K ⁻¹ [1]. La conductivité thermique des nanotubes (κ _TNT ) excluant l'impact de la porosité peut être estimé en utilisant des modèles de conductivité thermique effective donnés par l'Eq. 4 [1, 49], qui pour le cas des pores non conducteurs se réduit à l'Eq. 5 [1] :

où κ _eff est la conductivité thermique effective qui inclut l'effet de porosité, κ _aérien est la conductivité thermique de l'air, et P est la porosité. La conductivité thermique du TNT_A,T estimé à partir de l'éq. 4 est compris entre 0,44 et 0,61 W m ⁻¹ K ⁻¹ pour TNT_A,T . En utilisant le modèle de conductivité thermique effective (Eq. 4), la conductivité thermique des nanotubes de titanate purs avec des dimensions approximativement similaires a été rapportée comme étant de 0,40 à 0,84 W m ⁻¹ K ⁻¹ [1]. Nos résultats concordent bien avec les valeurs rapportées lorsque le même modèle efficace de conductivité thermique (Eq. 4) est utilisé.

Néanmoins, la forme des entrefers dans les nanotubes compacts n'est que partiellement aléatoire car les tubes eux-mêmes ont une forme non aléatoire. Afin de tenir compte de la forme différente des pores, un modèle analytique applicable à une gamme complète de porosités a été dérivé par Bauer [49] sur la base de la résolution de l'équation de conduction thermique de Laplace. Cette équation peut être présentée sous la forme suivante :

Dans cette équation, ε est le facteur de forme ou facteur de correction lié à la forme des pores. Sa valeur rend compte des formes variables des pores. Pour les formes aléatoires de l'entrefer, ε est 2/3 [1, 27, 50] réduisant ainsi l'Eq. 5 à Éq. 6.

Les valeurs des facteurs de forme ont été estimées pour les formes polyédriques par Yang et al. [50], basé sur la modélisation de facteurs de forme compris entre 1 et 1,48. Lors de l'ajustement de nos données à l'équation. 6, le meilleur ajustement (voir Fig. 4) est obtenu pour le facteur de forme ε ayant la valeur de 1,24. Sur la base de l'ajustement, la conductivité thermique pour le TNT_A est de 1,07 W m ⁻¹ K ⁻¹ . Cette valeur est légèrement inférieure aux valeurs signalées précédemment, 1,12 W m ⁻¹ K ⁻¹ pour les matrices de nanotubes anatase [34] et 1,5 W m ^− 1 K ^− 1 pour un seul nanotube d'anatase [32]. En conséquence, la conductivité thermique du TNT_Amor est de 0,98 W m ⁻¹ K ⁻¹ . La valeur légèrement inférieure de la conductivité thermique dans les nanotubes amorphes par rapport au TNT_A est attribuée à leur structure amorphe. Des valeurs de conductivité thermique plus faibles des nanotubes de dioxyde de titane amorphes que celles des nanotubes cristallins ont également été rapportées dans [32, 34]. Généralement, les films et matériaux amorphes sont connus pour avoir une conductivité thermique inférieure à celle des matériaux cristallins, bien qu'à une si petite échelle d'autres facteurs influencent également les valeurs de conductivité thermique. Par exemple, Wingert et al. [30] ont rapporté une conductivité thermique 30 % inférieure pour les nanotubes de silicium cristallin par rapport à leurs homologues amorphes de dimensions similaires. La conductivité thermique sous-amorphe de ces nanotubes a été attribuée au fort effet de ramollissement élastique dans les nanotubes cristallins [30]. À titre de comparaison avec les films amorphes, la conductivité thermique mesurée du film d'oxyde de titane amorphe de 100 nm déposé par le procédé ALD était de 1,29 W m ⁻¹ K ⁻¹ [47]. La conductivité thermique approchée par le modèle de Cahill et Pohl de la conductivité thermique minimale [37] était de 1,38 W m ⁻¹ K ⁻¹ pour le même film [47]. La conductivité thermique des films d'oxyde de titane amorphe déposés par pulvérisation cathodique était de 1,6 W m ⁻¹ K ⁻¹ pour des films de 920 nm d'épaisseur [38, 51]. La conductivité thermique obtenue pour les nanotubes est inférieure à celle des films d'oxyde de titane amorphe traités dans ces rapports [38, 47, 51]. Cependant, conductivité thermique comparativement plus faible de 0,7 W m ⁻¹ K ⁻¹ [52] a également été rapporté pour un film d'oxyde de titane amorphe de 150 nm d'épaisseur préparé par pulvérisation cathodique et 0,9 W m ⁻¹ K ⁻¹ [53] pour un film de 120 nm d'épaisseur préparé par méthode sol-gel. Dans le cas des films, la résistance thermique à la frontière entre le substrat, le film mince et le film transducteur métallique a été considérée comme abaissant la conductivité thermique globale en dessous de la limite amorphe [52]. Dans le cas des nanotubes, des facteurs tels que la résistance de contact thermique entre les nanotubes, la rugosité de surface et les impuretés dans la structure dues au processus de préparation affectent également la conductivité thermique nette. Guo et al. [34] ont proposé la valeur plus élevée de la résistance de contact thermique entre les réseaux de nanotubes amorphes par rapport aux nanotubes cristallins. Conductivité thermique de 0,85 W m ⁻¹ K ⁻¹ a été rapporté pour un seul nanotube amorphe [32], tandis que Guo et al. [34] ont signalé une conductivité thermique de 0,617 W m ⁻¹ K ⁻¹ pour les réseaux de nanotubes amorphes le long de la direction du tube. Pour TNT_A,T , conductivité thermique de 0,75 W m ⁻¹ K ⁻¹ Est obtenu. Cette valeur est en bon accord avec les résultats publiés pour les nanotubes de titanate [1, 33] préparés par méthode hydrothermale. Il est également noté que la conductivité thermique augmente avec l'augmentation de la densité du matériau indiqué dans le tableau 1. La densité mesurée de TNT_A (3,79 g cm ⁻³ ) est proche de la densité apparente d'anatase de 3,89 g cm ⁻³ [34]. La densité de TNT_A,T est également bien corrélé avec la densité mesurée des compacts de nanostructures mixtes de titanate et de dioxyde de titane [54]. La TNT_Amor a une densité de 3,67 g cm ⁻³ , ce qui est proche de la densité rapportée du film d'oxyde de titane amorphe (3,73 g cm ⁻³ ) déposé par ALD [55]. La dépendance linéaire de la conductivité thermique avec la densité a déjà été signalée pour les films d'alumine avant [55].

Le libre parcours moyen des phonons a été calculé comme étant de 2,5 nm pour l'oxyde de titane [1], de 1,21 à 3,15 nm pour les nanofibres d'oxyde de titane [28] et de 2 à 3 nm pour les nanotubes d'oxyde de titane [32]. Sur les trois différents types de nanotubes étudiés dans le présent rapport, les nanotubes anatase (TNT_A ) donnent la valeur de conductivité thermique la plus élevée, tandis que la conductivité thermique du TNT à parois multiples_A,T est inférieur à celui de TNT_A et TNT_Amor . La comparaison des valeurs de conductivité thermique actuelles et précédemment publiées en ce qui concerne l'épaisseur de paroi des TNT est illustrée à la Fig. 5. 32], et les valeurs des nanotubes produits par le présent RBA et les méthodes de traitement chimique sont tracées avec leurs valeurs moyennes d'épaisseur de paroi et de conductivités thermiques (Fig. 5). La figure 5 montre que la conductivité thermique des nanotubes d'oxyde de titane cristallin est considérablement réduite en réduisant l'épaisseur de la paroi. La suppression de la conductivité thermique avec la réduction de l'épaisseur de paroi est attribuée au confinement des phonons avec l'épaisseur de paroi [32]. Bien que cet effet n'ait pas été observé par Brahmi et al. [32], évidemment en raison de la limitation des échantillons aux dimensions réduites, la réduction proposée est observée avec le TNT actuel_A,T . La figure 5 montre une tendance similaire pour les nanotubes amorphes avec une réduction de la conductivité thermique avec l'épaisseur de la paroi. Généralement, les nanomatériaux amorphes devraient avoir une conductivité thermique similaire indépendamment de l'échelle, car le transport thermique est attribué aux diffusons non propagés [47]. Selon le matériau et ses dimensions, les propagones (propagateurs de vibrations) peuvent également contribuer à la conductivité thermique globale [35]. Wingert et al. [35] ont proposé la réduction de la conductivité thermique pour les films de silicium amorphe en réduisant l'épaisseur du film du micromètre au nanomètre. Plus tard, la réduction de la conductivité thermique dépendant de la taille pour le silicium amorphe a été confirmée expérimentalement par Kwon et al. [36] en raison de la contribution des propagones dans le transport thermique global. Le libre parcours moyen des propagones pour le silicium amorphe s'est avéré être compris entre 10 nm et 10 μm et ils ont contribué à une augmentation de 30 % de la conductivité thermique à température ambiante [36]. Le libre parcours moyen de l'oxyde de titane amorphe a été estimé entre 0,195 et 0,201 nm (≈  distance interatomique) [56]. Aucune étude n'a été trouvée indiquant le libre parcours moyen des propagones dans l'oxyde de titane. Cependant, la réduction de la conductivité thermique avec la diminution de l'épaisseur de paroi est également observée pour les TNT amorphes (Fig. 5). Il est donc supposé que le transport thermique dans les TNT est attribué non seulement aux diffusons, mais les propagones peuvent également contribuer à la conductivité thermique globale, ce qui réduit la conductivité thermique des nanotubes amorphes avec la réduction des dimensions de la paroi.

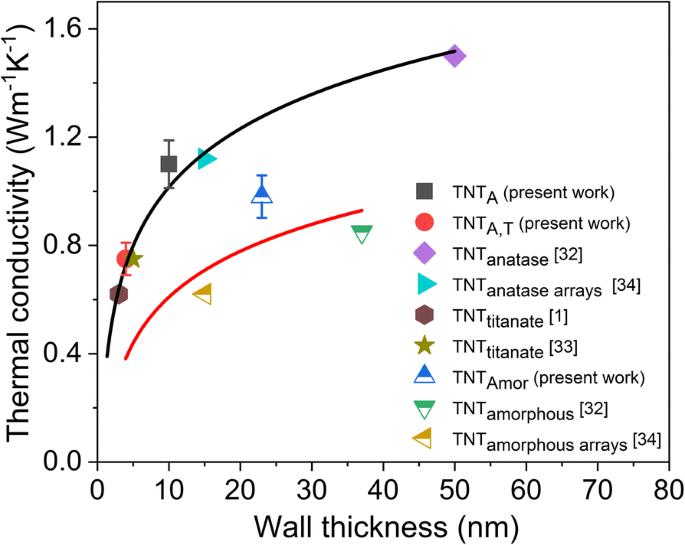
La conductivité thermique des nanotubes de dioxyde de titane cristallins et amorphes par rapport à leur épaisseur de paroi. Les lignes de tendance sont ajoutées pour un guidage visuel

Il a été proposé que les propriétés thermiques des nanotubes dépendent de leur épaisseur de paroi plutôt que du diamètre [1, 32]. Gao et Jelle ont présenté une approximation théorique pour la réduction de la conductivité thermique avec l'épaisseur de paroi [1], qui était une modification d'un modèle proposé précédemment [44]. Cependant, la conductivité thermique globale a également été affectée par la rugosité de la surface des nanotubes. Liang et Li [44] ont proposé la formule analytique pour la conductivité thermique des nanomatériaux semi-conducteurs, y compris les effets de confinement de la taille, la longueur de la cristallinité et la diffusion de surface des phonons par le paramètre de rugosité de surface (p ) comme suit :

où κ _TNT est la conductivité thermique du nanomatériau, κ _B est la conductivité thermique apparente, l _o est le libre parcours moyen du phonon, L est l'épaisseur de paroi, et L _o is the critical size at which almost all atoms of a crystal are located on its surface [44]. It should be noted that L _o  = 2(3 − d )w , where d is the dimension of the material (which is 1 in the case of nanotubes) and w is the atomic or molecular diameter [1, 44]. Finally, α is a material constant = 2Sv /3R  +  1, where Sv is the bulk vibrational entropy and R is the ideal gas constant [44]. The phonon mean free path of the titania nanotubes calculated from the kinetic formula of lattice thermal conductivity was reported to be 2.5 nm [1]. The bulk thermal conductivity of titania (κ _B ) is 8.5 W m ⁻¹ K ⁻¹ as noted previously. The values for w , Sv , and α are obtained from the study by Gao and Jelle [1]. The surface roughness factor p obtains values from 0 to 1, where smaller value of p corresponds to a rougher surface and diffusive phonon scattering and larger values correspond to smooth surfaces with specular phonon scattering [1, 32, 44]. Figure 6a shows the thermal conductivities of crystalline nanotubes for different wall thicknesses and scattering factors. The p factor of 0.4 was found best for estimating the thermal conductivity of 2-nm rutile nanoparticles in [57] as well as for silicon nanowires having the diameter of 20–100 nm in [44]. The same p value of 0.4 has also been used for titanate nanotubes by Gao and Jelle [1], who theoretically estimated thermal conductivity values of TNTs between 0.30 and 0.77 W m ⁻¹ K ⁻¹ for 2–3-nm wall thickness. Contrary to the previous reports, by using Eq. 7 our experimental data for TNT_A,T fit with the p factor of 0.26 as shown in Fig. 6a. The practical value is plotted at a maximum wall thickness. For TNT_A , the thermal conductivity value obtained by using Eq. 7 at the maximum wall thickness (12 nm) fits with the calculated surface roughness factor of 0.18. These small values are associated with the rough surface of the anodized nanotubes. The p factor corresponds to p =  1 − 10η /L , where η is the surface roughness of nanotubes and L is the thickness of the material [44]. This equation gives the approximation of surface roughness of 0.22–0.29 nm for TNT_A,T and 0.56–0.96 nm for TNT_A . These values correlate quite well with the roughness values estimated from the TEM micrographs. The difference in surface roughness for both nanotubes results from the synthesis process. It is pointed out that the thermal conductivity increases with increasing wall thickness for both crystalline nanotubes. This provides experimental verification for the model proposed by Liang and Li [44] and modified for nanotubes by Gao and Jelle [1], where thermal conductivity increases with an increase in wall thickness. The decline in the wall dimensions leads to the reduced phonon mean free path by phonon confinement and increased diffuse phonon boundary scattering, resulting in overall reduction in thermal conductivity values [32]. The crystal defects as well should influence the net thermal conductivity value along with the thermal contact resistance between the nanotubes, which are not considered here. Equation 7 is also adapted for the amorphous nanotubes (TNT_Amor ) and the maximum value of wall thickness (30 nm) is plotted in Fig. 6b. The bulk thermal conductivity (κ _B ) of the titania is estimated as 1.6 W m ⁻¹ K ⁻¹ [38] from the minimum thermal conductivity model and l _o is estimated as 0.198 nm [56]. The experimental value fits well with the p factor of 0.65 for amorphous nanotubes, which gives the surface roughness of 0.99–1.98 nm for the TNT_Amor . The mean roughness of TNT_Amor estimated from the TEM images (1.5 nm) fits well with this theoretical range. The surface roughness in one-dimensional crystalline nanostructures (< 100 nm) has a strong impact on the overall thermal conductivity reduction due to the diffusive phonon boundary scattering [58, 59]. In the case of amorphous material, the surface roughness could play a role if it approaches the wavelength of the propagons [36].

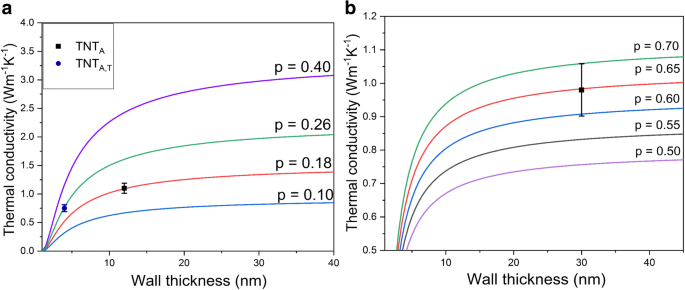
Size-dependent thermal conductivity of a crystalline titania nanotubes (TNT_A and TNT_A,T ) et b amorphous nanotubes (TNT_Amor ) with different surface roughness factors; symbols show the experimental thermal conductivity of the studied titania nanotubes and the solid lines indicate the calculated thermal conductivities by using Eq. 6

Conclusions

Three different kinds of titania nanotubes are synthesized with different crystal structure and morphology by using chemical processing and rapid breakdown anodization methods. Based on the measurement results at room temperature, the thermal conductivity of the titania nanotubes is considerably lower as compared to the bulk titania. Titania (TNT_A ) nanotubes are single-walled with one end opened and other closed, and they have anatase structure and a wall thickness of 7–12 nm. The thermal conductivity of these nanotubes estimated by an effective model of thermal conductivity is 1.07 W m ⁻¹ K ⁻¹ . The amorphous nanotubes (TNT_Amor ) with a wall thickness of 15–30 nm have a thermal conductivity of 0.98 W m ⁻¹ K ⁻¹ . Their thermal conductivity is slightly lower than that of crystalline anatase nanotubes (TNT_A ). However, the multiwalled and open-ended nanotubes (TNT_A,T ) with a mixed crystal structure and a wall thickness of 4–5 nm have the lowest thermal conductivity of 0.75 W m ⁻¹ K ⁻¹ . This low value of thermal conductivity is due to the reduced dimensions of walls approaching the calculated 2.5-nm phonon mean free path. The reduction in the wall thickness is found to result in overall suppression of the thermal conductivity as the phonon confinement is enhanced and the phonon boundary scattering increased. The size confinement effects of phonon transport with different surface-related parameters for both crystalline and amorphous nanotubes are considered. Generally, the thermal conductivity of amorphous oxides is found independent of the size. Comparison of the present result on the amorphous nanotubes with those in the literature, however, suggests also size-dependent reduction in the thermal conductivity of the amorphous nanotubes. This may be due to the possible contribution of propagons in the overall thermal transport in disordered structure along with the diffusons. For TNT_A,T , the thermal conductivity value agrees well with the surface roughness factor of 0.26, while in the case of TNT_A nanotubes, it matches with 0.18 confirming the different surface roughness of the two kinds of crystalline nanotubes related to the synthesis processes. TNT_Amor surface roughness (1.5 nm) estimated from TEM micrographs is in line with the calculated surface roughness factor of 0.65.

Abréviations

RBA:

Rapid breakdown anodization

SEM :

Microscopie électronique à balayage

TEM :

Microscopie électronique à transmission

TNT_A :

Titania nanotubes with anatase crystal structure

TNT_A,T :

Titania nanotubes with mixed crystal structure (anatase and titanate)

TNT_Amor :

Titania nanotubes with amorphous structure

TNTs:

Titania nanotubes

XRD :

Diffraction des rayons X