Étude des propriétés structurelles, électroniques et magnétiques des amas Ag n V (n = 1–12)

Contexte

Au cours des dernières décennies, les amas d'argent ont attiré une attention particulière en raison de leurs propriétés optiques et catalytiques inhabituelles [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15, 16,17,18,19,20]. Simultanément, des recherches théoriques et expérimentales ont révélé qu'un atome dopé dans un petit amas d'un autre élément peut fondamentalement changer la nature de l'amas hôte [21,22,23,24,25,26,27,28,29,30,31 ,32,33,34,35,36,37,38,39,40,41,42,43,44]. On s'attend à ce que des amas d'argent dopés avec différents atomes adaptent les propriétés optiques, électroniques et magnétiques souhaitées à des applications potentielles en imagerie, détection, biologie, médecine et nanotechnologie [45,46,47,48,49,50,51,52 ,53,54,55]. Par exemple, le dopage de Si dans les amas d'argent conduit à un élargissement et à un amortissement des pics des spectres d'absorption UV-visible des amas d'Ag [45]. Le caractère optique de Ag _n Au _m peut être ajusté en changeant le rapport des atomes d'argent aux atomes d'or et Au₄ Ag₄ pourrait être un dispositif photoélectrique moléculaire potentiellement prometteur [46]. Contrairement aux amas d'argent, le TiO₂ binaire modifié par amas Ag-Au L'électrode améliore la densité de courant de court-circuit et les rendements de conversion de puissance maximale de la cellule solaire [47]. Les énergies d'adsorption d'un ensemble de ligands typiques (−COOH, −CN, −OH, −SH, −CH₃ , −NON₂ , −NH₃ , −NO) sont plus petites sur Ag₁₂ Au cluster que sur Ag₁₃ groupe [48]. Le nanoalliage Ag-Cu est un candidat potentiel pour remplacer le catalyseur à base de Pt noble dans les piles à combustible alcalines [49]. Les électrons dans les atomes externes de Ag₁₂ Les amas de Cu ont une caractéristique plus active que celle d'Ag₁₃ groupe [50]. L'activité catalytique du cluster d'alliages Ag-Pd pour la dissociation de l'hydrogène est étroitement associée à la stoechiométrie. L'Ag₆ Pd₂ est le cluster le plus efficace pour l'adsorption de molécules d'hydrogène et peut servir de candidat prometteur pour H₂ stockage [51]. L'introduction d'un seul atome de métal de transition 3D a résolu efficacement le problème d'instabilité de l'Ag₁₂ icosaèdre [52]. Récemment, plusieurs recherches ont été menées pour les amas d'argent dopé V en raison de leurs propriétés physiques et chimiques uniques [56,57,58,59]. Zhang et al. a signalé que le neutre Ag₁₂ L'amas V montre des énergies de liaison relatives plus importantes que l'Ag₁₃ pur icosaédrique groupe [56]. Chen et al. trouvé que Pyridine sur V@Ag₁₂ ⁻ clusters présente l'amélioration chimique la plus forte avec un facteur d'environ mille [57]. Medel et al. a exploré la nature de la transition de valence et du moment de spin dans Ag _n V ⁺ clusters qui ont une stabilité améliorée pour n = 14 [58]. Cependant, il existe relativement peu de travaux concernant les amas d'argent dopé V neutre. En particulier, les différents spectres d'Ag _n Les clusters V n'ont pas été obtenus mais seraient extrêmement utiles pour l'identification de la structure des clusters. Le motif structurel des amas d'argent dopé V doit également être exploré plus avant. Le changement de moment magnétique de l'impureté magnétique intégré dans un hôte non magnétique n'est toujours pas entièrement compris. En conséquence, dans le présent article, les propriétés géométriques, électroniques et magnétiques de Ag _n V (n = 1–12) les clusters seront systématiquement recherchés par la théorie de la fonctionnelle de la densité (DFT). On espère que ce travail pourra fournir une référence pour comprendre la relation entre la fonction et la structure des matériaux et pour les expériences associées.

Méthodes

L'exactitude des fonctions d'échange-corrélation distinctes, telles qu'implémentées dans le progiciel GAUSSIAN09 (Frisch, M. J. et al., Wallingford, KY, USA) [60], a d'abord été vérifiée par des calculs sur Ag₂ dimère. Les résultats calculés basés sur le niveau PW91PW91/LanL2DZ (Perdew, JP et al., La Nouvelle-Orléans, Louisiane, États-Unis) sont en bon accord avec les résultats expérimentaux [61, 62], comme résumé dans le tableau 1. D'autre part, les calculs des tests utilisant les différentes fonctionnelles DFT ont été réalisées pour le dimère AgV. Cinq fonctionnelles répertoriées dans le tableau 1 favorisent les mêmes configurations de spin. Ainsi, ce niveau de théorie est utilisé pour les optimisations géométriques et les analyses fréquentielles de Ag _n grappes en V. De très nombreuses configurations initiales d'Ag _n Les clusters V ont été construits en utilisant CALYPSO qui est une méthode efficace de prédiction de structure [63]. Dans cette méthode, l'évolution structurelle est réalisée par l'optimisation des essaims de particules (PSO) qui est une technique d'optimisation stochastique basée sur la population. La technique de la matrice de caractérisation des liaisons est utilisée pour améliorer l'efficacité de la recherche et éliminer les structures similaires. La caractéristique importante de CALYPSO ne nécessite que des compositions chimiques pour un cluster donné pour prédire sa structure. En raison de l'effet de polarisation de spin, chaque structure initiale a été optimisée aux états de spin possibles. Si une fréquence vibrationnelle imaginaire est trouvée, une relaxation de la structure instable sera effectuée jusqu'à ce que le minimum local soit réellement obtenu. Dans tous les calculs, les seuils de convergence ont été fixés à 6,0 × 10 ⁻⁵ Å pour le déplacement, 1.5 × 10 ⁻⁵ Hartree/Bohr pour les forces et 10 ⁻⁶ Hartree pour une énergie totale.

Résultats et discussions

Structures géométriques et spectres vibratoires

Pour Ag _n V (n = 1–12), une recherche structurale approfondie a été effectuée et de nombreux isomères ont été obtenus. La structure la plus stable et deux isomères de basse altitude pour chaque Ag _n Les clusters V sont affichés sur la figure 1. Selon les énergies de faible à élevée, ces isomères sont désignés par na, nb et nc, où n représente le nombre d'atomes d'Ag dans Ag _n grappe en V. Leur symétrie, multiplicité de spin et différence d'énergie par rapport à chacune des structures les plus stables sont également indiquées sur la figure. Quelques paramètres physiques de l'état fondamental Ag _n Les clusters V sont regroupés dans le tableau 2. Pendant ce temps, afin d'examiner les effets du dopant V sur les clusters d'argent, les optimisations géométriques de Ag _n (n = 2–13) les clusters ont été réalisés en utilisant la même méthode et le même ensemble de base. Les structures les plus énergétiques de Ag _n les clusters représentés sur la figure 1 concordent bien avec le rapport précédent [39].

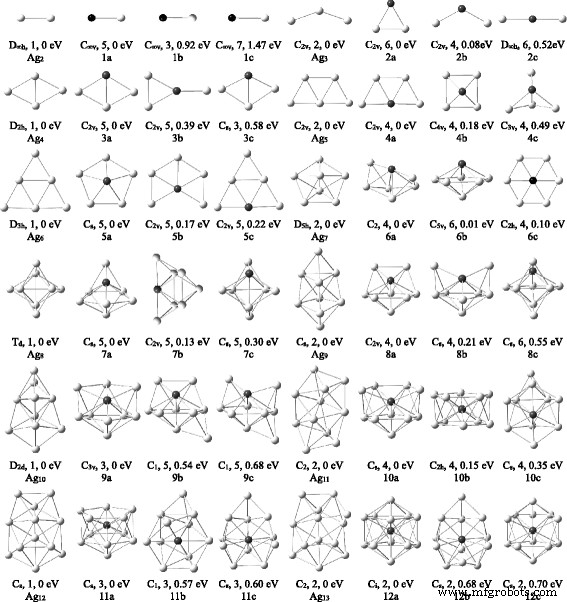
Les structures d'état fondamental de Ag _{n + 1} et Ag _n V (n = 2–12) grappes. Deux isomères de basse altitude pour Ag _n grappes en V. La symétrie, la multiplicité de spin et la différence d'énergie sont données en dessous. Les boules grises et noires désignent respectivement les atomes Ag et V

Les résultats optimisés pour le dimère AgV montrent que l'état de spin du quintette est énergétiquement inférieur aux états de spin triplet et septet de 0,92 et 1,47 eV, respectivement. Par conséquent, le quintette AgV est la structure de l'état fondamental. La structure la plus stable de Ag₂ L'amas en V est le triangulaire 2a avec C_2v symétrie. La configuration 2a à l'état de spin quatuor devient l'isomère 2b. Les isomères 3a et 4a, qui ressemblent aux structures les plus énergétiques de Ag₄ et Ag₅ clusters, sont l'état fondamental de Ag₃ V et Ag₄ grappes en V. La structure de l'état fondamental de Ag₄ Le cluster V est également en accord avec le résultat de Medel et al. [58]. L'isomère 4b avec l'atome V au sommet est une pyramide carrée et la première structure tridimensionnelle (3D). L'isomère 4c possède une structure bipyramide triangulaire et son énergie totale est supérieure à l'isomère 4a de 0,49 eV. D'autres isomères planaires et 3D sont moins stables que l'isomère 4c.

À partir de n = 5, les structures les plus énergétiques de Ag _n Les clusters V préfèrent les configurations 3D. Pour éviter de laisser de côté l'état fondamental, nous avions également utilisé les stratégies optimisées consistant à substituer un Ag par un atome de V de l'amas d'argent stable ou à ajouter un ou des atomes d'Ag à un petit Ag _n grappes en V. Les isomères 5a et 6a sont les structures les plus stables de Ag₅ V et Ag₆ grappes en V. Les deux isomères sont obtenus en déformant la géométrie de C_5v et C_2v aux C_s et C₂ groupes de points, respectivement. L'isomère 6a est inférieur de 0,62 eV dans l'état de spin en quartet par rapport à l'état de spin en sextuor. Les isomères 5c et 6b sont similaires aux structures de l'état fondamental de l'Ag₆ pur et Ag₇ groupes. L'isomère 6b est presque dégénéré avec l'isomère 6a. En raison de l'effet Jahn-Teller, l'isomère planaire 6c avec C_2h la symétrie a une légère déviation de D_2h symétrie.

En ce qui concerne Ag _n V (n = 7–12) clusters, le nombre d'isomères augmente rapidement avec l'augmentation de la taille des clusters. Les structures optimisées indiquent que les énergies de Ag _n Les clusters V avec la même configuration augmentent avec la diminution du nombre de coordination de l'atome V. En conséquence, divers Ag _n Les isomères V où l'atome V occupe la position avec le nombre de coordination le plus élevé ont été examinés plus avant pour s'assurer que les structures les plus stables sont le minimum global. Les structures les plus énergétiques de Ag₇ V, Ag₈ V, Ag₉ V, Ag₁₀ V, Ag₁₁ V et Ag₁₂ Les clusters V sont 7a, 8a, 9a, 10a, 11a et 12a sur la figure 1, respectivement. Leurs géométries sont qualitativement en accord avec les résultats de Medel et al. [58]. Ces structures sont entièrement différentes de la structure de l'état fondamental de l'Ag _{n correspondant + 1} amas et contiennent une bipyramide pentagonale. L'Ag _n Isomères V qui correspondent aux structures les plus énergétiques de Ag _{n + 1} des clusters se trouvent au-dessus de chacune des structures d'état fondamental (na). De plus, les 10b et 12a présentent un léger écart par rapport à D_5d et D_3d symétrie. La configuration de la cage de Ag₁₂ L'amas V, où l'atome V occupe la position centrale, n'est découvert que dans les états de spin les plus bas.

A partir des résultats optimisés, on constate que l'Ag _n Les clusters V ont une loi de croissance évidente. Le trapèze et l'icosaèdre sont deux cadres de base pour le processus de croissance d'Ag _n Amas en V, comme le montre la figure 2. La transition structurelle bidimensionnelle à tridimensionnelle pour Ag _n Le cluster V se produit à n =5. La taille de transition de Ag _n L'amas V est plus petit que celui des amas Ag purs (n = 6). Pour n = 5–12, les états fondamentaux de Ag _n Les clusters V sont évidemment distincts de ceux des Ag _{n + 1} groupes. L'atome V dans Ag _n L'amas V a tendance à occuper la position la plus coordonnée et est progressivement encapsulé au centre par les atomes d'Ag. Cela peut être attribué au principe du chevauchement maximal dans la théorie des liaisons chimiques des complexes. Étant donné que les atomes Ag et V ont un chevauchement orbital plus important dans les circonstances ci-dessus, l'énergie de Ag _n L'amas V, qui est également lié à l'arrangement des atomes d'Ag, sera plus faible et l'amas correspondant sera alors plus stable.

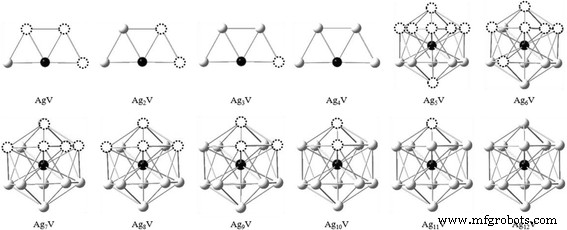
Le diagramme de croissance de Ag _n V (n = 1–12) grappes

Les spectroscopies infrarouge et Raman sont des outils puissants pour l'identification de la structure des clusters et des composants matériels. Généralement, l'identification structurelle est accomplie en comparant les résultats expérimentaux avec les prédictions théoriques, ce qui est une partie indispensable. En conséquence, les spectres infrarouges et les spectres Raman des Ag _{n les plus stables} V (n = 1–12) les amas sont affichés sur la Fig. 3. Le spectre infrarouge montre les vibrations asymétriques du groupe polaire. Le spectre Raman révèle les vibrations symétriques du groupe non polaire et du squelette. Les dimères AgV ont les mêmes spectres infrarouge et Raman. Pour les autres Ag _n Amas V, la forte absorption du spectre infrarouge a un faible pic dans le spectre de diffusion Raman. Au contraire, le pic de diffusion Raman est fort et l'absorption infrarouge est faible. La position du pic dans les deux types de spectres pour tous les isomères est comprise entre 15 et 270 cm ⁻¹ . Le pic le plus intense dans le spectre infrarouge de chaque Ag _n Les clusters V sont liés à la vibration d'étirement Ag-V.

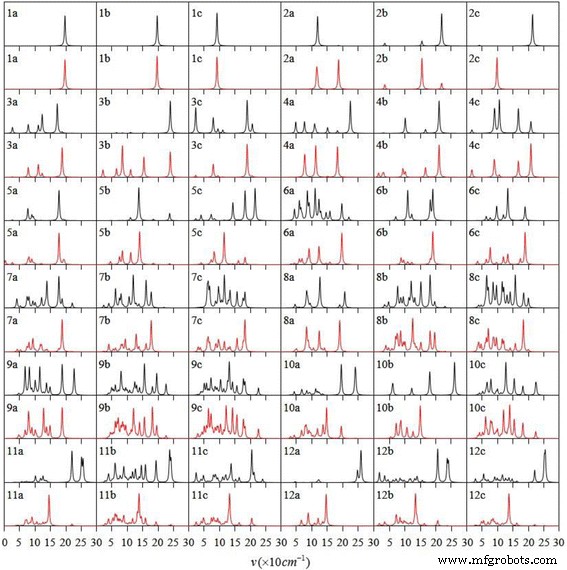
Les spectres infrarouge (noir) et Raman (rouge) de l'état fondamental et de deux isomères de basse altitude de Ag _n V (n = 1–12) grappes

Propriétés électroniques

Le potentiel d'ionisation vertical (VIP) et l'affinité électronique (EA) sont deux grandeurs principales pour sonder les propriétés électroniques et peuvent être calculés comme suit :

où E (cluster cationique) et E (amas anionique) sont les énergies ponctuelles des amas cationiques et anioniques dans la géométrie de l'amas neutre. Pour la plus basse énergie Ag _{n + 1} et Ag _n Clusters V, le tableau 3 répertorie les valeurs VIP, EA calculées et les valeurs expérimentales disponibles. Les VIP et EA calculés de Ag _{n + 1} les clusters sont en ligne avec leurs données mesurées. Cette cohérence confirme à nouveau la fiabilité de l'approche théorique actuelle. De plus, on note que le dimère AgV a le plus gros VIP et le plus petit EA. Cela implique qu'AgV est difficile à perdre ou nécessite un électron. L'icosaédrique Ag₁₂ L'amas V a le plus grand EA et il est facile d'obtenir un électron de plus. Offrir du matériel de référence pour l'expérience de spectroscopie photoélectronique dans l'après-temps, les spectres photoélectroniques théoriques (PES) de l'état fondamental et deux structures basses d'Ag _n V (n = 1–12) les clusters ont été simulés en ajoutant le premier VIP à chaque énergie orbitale occupée par rapport à l'HOMO et en les adaptant avec un schéma d'expansion de Lorentz et un facteur d'élargissement de 0,1 eV, comme le montre la figure 4. La distribution du niveau d'énergie de ces clusters est compris entre 5,5 et 12 eV. Les expérimentateurs peuvent utiliser les spectres PES pour distinguer ces clusters.

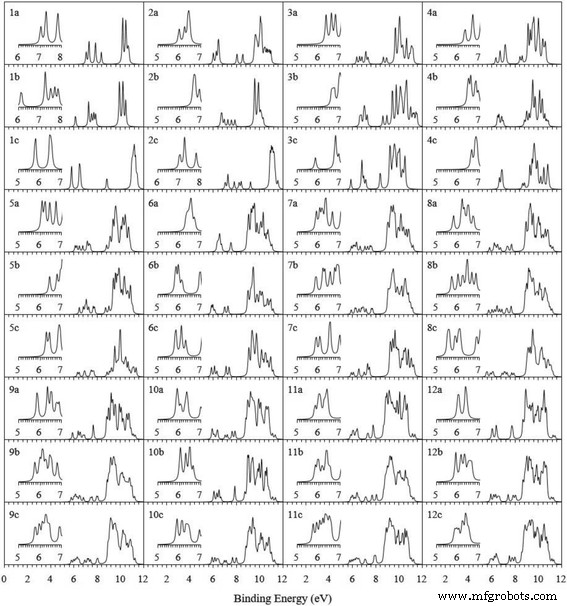
PES simulé de l'état fondamental et de deux isomères de basse altitude de Ag _n V (n = 1–12) grappes

Afin d'examiner l'influence de l'atome V sur la stabilité des amas d'argent, les énergies de liaison atomiques moyennées (E _b ) de l'Ag _{n le plus stable + 1} et Ag _n Les clusters V peuvent être estimés comme suit :

où E (Ag), E (Ag _{n + 1} ), E (V)_, et E (Ag _n V) sont les énergies de l'atome Ag, de l'amas d'argent, de l'atome V et d'Ag_n cluster V, respectivement. Les énergies de liaison calculées par atome pour l'Ag _{n le plus stable + 1} et Ag _n Les clusters V sont représentés sur la figure 5. Il ressort clairement de cette figure que le E _b d'Ag _n Le cluster V est une fonction croissante monotone de la taille du cluster et plus grand que celui de Ag _{n + 1} cluster pour n ≥ 2. Surtout, le E _b d'amas dopé augmentent rapidement pour les structures planaires et progressivement pour les structures 3D. Cela signifie que la force de liaison entre les atomes devient de plus en plus forte au cours du processus de croissance. La substitution d'un atome V pour un atome Ag dans Ag _{n + 1} (n ≥ 2) les clusters peuvent évidemment améliorer la stabilité des clusters hôtes. D'autre part, l'énergie de liaison de l'amas diatomique doit être étroitement liée à la longueur de la liaison. Le E _b d'AgV dimère est plus petit que celui d'Ag₂ . Le changement anormal peut être attribué au fait que la distance de liaison d'AgV (2,61 Å) est plus longue que celle d'Ag₂ (2,58 Å).

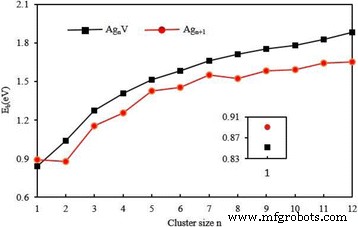
Les énergies de liaison moyennes de l'énergie la plus basse Ag _{n + 1} et Ag _n V (n = 1–12) grappes

La stabilité thermique des clusters peut être examinée par l'énergie de dissociation (DE), qui est différente pour les canaux de dissociation distincts. Le canal de dissociation le plus basique est la division d'un cluster plus grand en deux clusters plus petits. Le DE correspondant est petit par rapport aux autres canaux de dissociation. Par conséquent, les canaux de dissociation ultérieurs sont étudiés pour l'Ag _{n le plus stable} V (n = 1–12) grappes.

où m n'est pas supérieur à n . Les DE des canaux de dissociation ci-dessus sont définis comme suit :

où E représente l'énergie de l'amas ou de l'atome correspondant. Les DE d'Ag _n Les clusters V pour les différents canaux de dissociation ont été répertoriés dans le tableau 4. Le petit DE indique que le canal de dissociation correspondant est facile à mettre en place. C'est-à-dire que le canal de dissociation correspondant au DE minimum est le plus susceptible de se produire. On peut voir à partir du tableau 4 que les canaux de dissociation les plus préférés de Ag _n Les clusters V sont Ag _n V = Ag + Ag _{n − 1} V pour n = 1 et 4-12 et Ag _n V = Ag₂ + Ag _{n − 2} V pour n = 2 et 3. Le DE minimum (2,54 eV) de Ag₁₂ Le cluster V est le plus grand de tous les clusters dopés, ce qui implique que le cluster icosaédrique est plus stable que les autres clusters. De plus, nous trouvons que la tendance de changement du DE minimum de l'Ag neutre 3D _n V (n = 5–12) l'amas est le même que celui des abondances de l'Ag cationique _n V ⁺ groupe [64, 65]. Cependant, il n'y a pas une telle relation entre planaire Ag _n V et Ag _n V ⁺ pour n = 2–4.

L'écart énergétique (E _g ) entre l'orbitale moléculaire occupée la plus élevée (HOMO) et l'orbitale moléculaire inoccupée la plus basse (LUMO) est toujours considérée comme une quantité importante qui caractérise l'activité chimique des petits amas métalliques. Un écart énergétique important est lié à une stabilité chimique élevée. Pour l'état fondamental Ag _{n + 1} et Ag _n Amas en V, la Fig. 6 montre les écarts énergétiques en fonction de la taille des amas. Une alternance impair-pair est observée dans les lacunes énergétiques des amas d'argent pur. Cette alternance peut s'expliquer par l'effet d'appariement des électrons, c'est-à-dire que l'effet de protection électronique de deux électrons occupant le même HOMO est beaucoup plus petit que celui de deux électrons occupant des orbites différentes. Un atome Ag ([Kr]4f ¹⁴ 4d ¹⁰ 5s ¹ ) en Ag _{n + 1} cluster est remplacé par un V ([Ar]3d ³ 4s ² ) atome. Pour les n impairs , la coque fermée de Ag _{n + 1} cluster est remplacé par le shell ouvert de Ag _n grappe en V. Bien sûr, le E _g d'Ag _n Amas en V avec n impair est inférieur à celui de Ag _{n + 1} groupe. Cette diminution est très évidente. Même pour n , les deux Ag _{n + 1} et Ag _n Les clusters V ont un shell sans restriction. Le E _g devrait dépendre de leurs structures. Dans ce cas, notons que le E _g d'Ag _n V (n = 2 et 4) le cluster à structure planaire est plus petit que celui de Ag _{n + 1} cluster et le E _g d'Ag _n V (n = 6, 8, 10 et 12) cluster avec structure 3D est un peu plus grand que celui de Ag _{n + 1} groupe. En général, la substitution d'un atome V pour un atome Ag dans Ag _{n + 1} clusters avec même n a peu d'effet sur l'écart énergétique du cluster hôte.

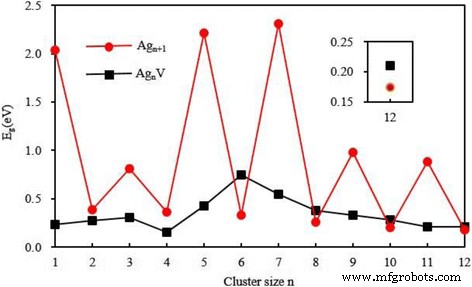
Les lacunes énergétiques HOMO-LUMO de l'état fondamental Ag _{n + 1} et Ag _n V (n =1-12) clusters

Propriétés magnétiques

La propriété magnétique du cluster est fréquemment utilisée dans la préparation de dispositifs nanoélectroniques et de matériaux de stockage magnétique à haute densité. Le moment magnétique total de l'amas se compose du moment magnétique de spin et du moment magnétique orbital des électrons. Le moment magnétique de spin d'un électron est beaucoup plus grand que le moment magnétique orbital et, par conséquent, le moment magnétique de l'amas est dominé par le moment magnétique de spin. Le moment magnétique total de l'énergie la plus basse Ag _n V clusters (n = 1–12) a été calculé et est présenté sur la Fig. 7, où nous avons également tracé le moment magnétique total des amas hôtes. Les moments magnétiques des Ag _{n les plus stables + 1} les clusters sont complètement éteints pour les n impairs et sont 1 μ_B pour même n . Le petit Ag _n Les amas V ont un grand moment magnétique. Avec l'augmentation de la taille de l'amas, le moment magnétique de Ag _n V clusters diminue en vagues. Lorsque n = 12, l'Ag₁₂ V a le même moment magnétique que Ag₁₃ groupe. Cela signifie que le dopage de l'atome V ne peut qu'améliorer le magnétisme des petits amas d'argent. Pour tenter de tenir compte du magnétisme, la figure 8 montre la densité d'états de spin (SDOS) pour l'état fondamental Ag _n grappes en V. Il ressort clairement de cette figure que l'Ag _n Les clusters V ont des domaines magnétiques qui diminuent avec l'augmentation de la taille des clusters. Toutes les structures de plus basse énergie ont une bande forte entre − 5 eV et − 2,5 eV, qui est composée principalement de la valence s et d orbitales des atomes Ag et V. Les niveaux d'énergie près du HOMO, E − E _HOMO =  − 1~0 eV, joue un rôle clé dans la détermination du comportement magnétique de Ag _n V clusters.

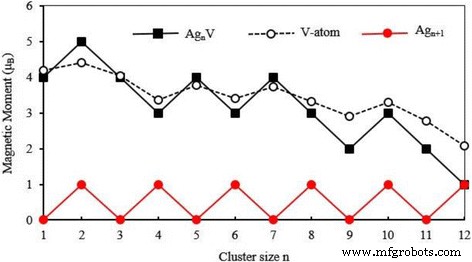
Moment magnétique total de l'état fondamental Ag _{n + 1} et Ag _n V (n = 1–12) amas et moment magnétique local sur l'atome V

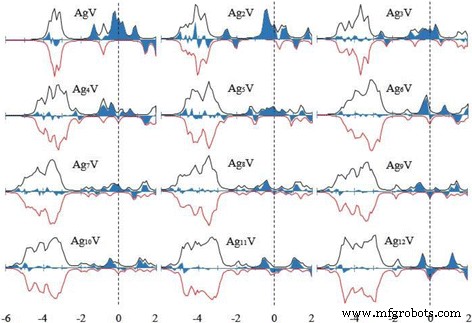
Le SDOS de l'état fondamental Ag _n V (n = 1–12) grappes. Le spin up est positif et le spin down est négatif. Un facteur d'élargissement δ = 0.1 eV est utilisé. La rotation vers le haut moins la rotation vers le bas est la partie bleue. La ligne pointillée indique l'emplacement du niveau HOMO

Pour explorer davantage les propriétés magnétiques, nous avons effectué l'analyse orbitale des liaisons naturelles pour l'Ag _{n le plus stable} Amas en V [66]. Les moments magnétiques locaux sur l'atome V sont 4.18 μ _B pour AgV, 4,41 μ _B pour Ag₂ V, 4.03 μ _B pour Ag₃ V, 3,36 μ _B pour Ag₄ V, 3,78μ _B pour Ag₅ V, 3,40 μ _B pour Ag₆ V, 3,73 μ _B pour Ag₇ V, 3,33 μ _B pour Ag₈ V, 2,91 μ _B pour Ag₉ V, 3,29 μ _B pour Ag₁₀ V, 2,77 μ _B pour Ag₁₁ V, et 2,08 μ _B pour Ag₁₂ V, comme le montre la figure 7. Dans l'ensemble, le moment magnétique de l'atome V diminue progressivement avec l'augmentation de la taille des amas. Le moment magnétique fourni par les atomes Ag est très petit. De plus, sauf pour Ag₂ V, Ag₅ V et Ag₇ Amas V, le moment magnétique total des atomes Ag dans d'autres amas dopés présentent l'alignement antiferromagnétique par rapport au moment magnétique de l'atome V. En d'autres termes, les moments magnétiques totaux de tous les Ag _n Les amas V sont principalement dérivés de l'atome V paramagnétique, comme le montre la figure 7.

Le moment magnétique local et la charge sur 4s , 3d , 4p , et 4d coquilles d'atome V dans la plus basse énergie Ag _n Le cluster V est répertorié dans le tableau 5. On peut voir à partir de ce tableau que le 3d partiellement occupé coquille joue un rôle crucial dans la détermination du magnétisme de l'atome V et son moment magnétique est de 2,01 à 3,82 μ _B . Les 4s et 4p les coquilles, qui sont non magnétiques pour un atome V libre, produisent un peu du moment magnétique. Le 4d la coquille est presque non magnétique. Le prélèvement le 3j et 4p obus augmente de 0,77 à 1,97 et 0,03 à 2,41 e respectivement. Surtout, la charge sur le 4p orbital augmente avec l'augmentation de la taille des amas. Très peu de charges se retrouvent sur le 4d orbite de l'atome V dans Ag _n V (n = 4–12) cluster. Néanmoins, la charge sur 4s shell réduit de 1,02 à 1,54 e . Le transfert de charge laisse entendre que l'atome V dans Ag _n Les clusters V ont une hybridation entre les s , p , et d coquilles. Comme nous le savons, l'atome V isolé possède cinq électrons de valence. En même temps, la charge de l'atome V dans Ag _n Le cluster V peut être obtenu à partir du tableau 5. À partir du principe de conservation de charge, 0,10-0,21 e transfert de l'atome V aux atomes Ag pour le planaire Ag _n V (n = 1–4) clusters, tandis que 0,35–2,92 e des atomes Ag à l'atome V pour le Ag _{n 3D} V (n = 5–12) clusters, comme illustré à la Fig. 9. Si M et C désignent le moment magnétique et l'électron de valence de l'atome V dans Ag _n V clusters, à la fois la variation du moment magnétique (ΔM = M − 3) et transfert de charges (ΔC = 5 − C ) ont la même tendance changeante, comme indiqué sur la Fig. 10. On peut conclure à partir de la Fig. 10 que le transfert de charge devrait être la raison de la modification du moment magnétique de l'atome V dans Ag _n V clusters.

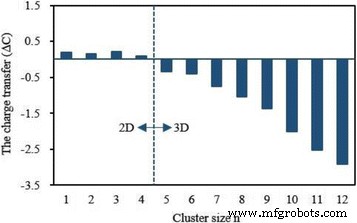
Le transfert de charge de l'atome V dans l'Ag _{n le plus stable} V (n = 1-12) grappes. Atome V libre comme point de référence

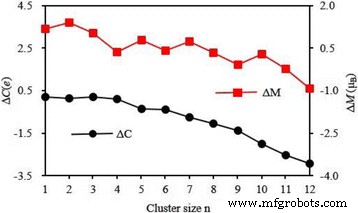
Le transfert de charge (ΔC) et le changement de moment magnétique (ΔM) de l'atome V dans l'Ag _{n le plus stable} V (n = 1-12) groupes