Contrôle de la double non-linéarité des propriétés de mode et de dispersion dans le guide d'ondes plasmonique graphène-diélectrique

Contexte

La plasmonique du graphène a attiré une large attention [1,2,3,4] en raison des caractéristiques électroniques et optiques uniques du graphène par rapport aux métaux. À THz et dans la gamme de fréquences infrarouge lointain, la transition intrabande des électrons domine et le graphène se comporte comme un métal. Par conséquent, les polaritons de plasmon de surface (SPP) pourraient être pris en charge par le graphène. Pour la structure composite multicouche graphène-diélectrique, les modes d'excitation, de couplage et de propagation des SPP ont été étudiés. Le mode électromagnétique quasi-transversal a été trouvé dans un guide d'ondes à plaques parallèles en graphène [5]. Le couplage des SPP a été étudié [6, 7] dans une structure multicouche graphène-diélectrique. Pour la structure de réseau périodique de feuille de graphène monocouche, un fort couplage entre les SPP apparaît lorsque les feuilles de graphène sont disposées étroitement.

Des efforts considérables ont été consacrés à l'étude des propriétés optiques des structures composites non linéaires graphène-diélectrique [8,9,10,11,12] pour leur grand potentiel dans le contrôle de la propagation de la lumière aux micro et nano-échelles. Pour le cas du graphène monocouche, les plasmons de surface à l'interface entre le graphène et le substrat non linéaire de type kerr ont été discutés [8]. Il est montré que la longueur d'onde des plasmons de graphène peut être réglée en ajustant la permittivité non linéaire des substrats. Pour la structure multicouche diélectrique non linéaire graphène, les propriétés de propagation et de localisation des plasmons de graphène ont été explorées et les relations de dispersion exactes pour les plasmons de surface TM d'un guide d'ondes à plaques parallèles en graphène ont été obtenues [11]. La longueur de propagation et de localisation est remarquablement affectée par l'ajustement des permittivités non linéaires. Récemment, la relation de dispersion pour les modes plasmon symétrique et antisymétrique a été dérivée dans une structure de dalle Kerr recouverte de graphène [12]. À l'exception du mode de propagation vers l'avant typique, les modes symétrique et antisymétrique ont été trouvés.

Sur la base de la forte non-linéarité du graphène, plusieurs effets optiques non linéaires ont été prédits [13,14,15,16,17]. Nesterov et al. [15] ont étudié la propagation non linéaire de la lumière dans une monocouche de graphène et ont découvert que la monocouche de graphène peut prendre en charge les solitons optiques spatiaux TE et TM à des fréquences optiques en raison de la non-linéarité intrinsèque du graphène. Plus récemment, en remplaçant le graphène monocouche par du graphène multicouche, Smirnova et al. [16] ont étudié les propriétés non linéaires d'un empilement multicouche de feuilles de graphène et ont dérivé les équations non linéaires décrivant la dynamique spatiale des plasmons non linéaires. Les études précédentes se sont principalement concentrées sur l'influence de la non-linéarité unique sur le contrôle des propriétés de la lumière dans les structures diélectriques en graphène. L'idée d'un double contrôle de non-linéarité a été introduite dans les super-réseaux photoniques à base de graphène [18, 19], dans lesquels le contrôle électrique et tout optique des faisceaux photoniques avec une précision de sous-longueur d'onde profonde a été réalisé. Cependant, le double contrôle de non-linéarité des propriétés de mode et de dispersion dans la structure plasmonique graphène-diélectrique laisse encore de nombreuses questions ouvertes. Par conséquent, dans cet article, nous considérons simultanément la non-linéarité du graphène et du diélectrique dans le guide d'onde graphène-diélectrique-graphene et étudions l'influence de la double non-linéarité sur les propriétés de couplage et de dispersion des modes.

Méthodes

Le guide d'ondes plasmonique diélectrique non linéaire graphène est illustré schématiquement sur la figure 1, une plaque parallèle de graphène avec une conductivité σ _g est placé à x = ± d /2, où le diélectrique est un milieu de type Kerr avec une permittivité ε = ε _L + α |E | ² . Dans notre analyse, le graphène est traité comme une frontière en raison de son épaisseur à l'échelle d'un atome. Considérant un SPP magnétique transversal (TM) qui se propage le long de z direction avec une constante de propagation β et décroît de façon exponentielle le long du x direction dans l'air et le milieu non linéaire, respectivement.

Schéma de principe du guide d'ondes plasmonique non linéaire graphène-diélectrique-graphene

Pour la polarisation TM, on sait qu'il y a trois composantes de champ E _x , E _z , et H _y . Le champ magnétique H = H _y y et champ électrique E = E _x x + E _z z satisfaire les équations

où ε ₀ et μ ₀ sont la permittivité électrique et la perméabilité magnétique du vide. De l'éq. (2) et ε = ε _L + α |E | ² nous pouvons obtenir

En substituant l'équation. (5) dans l'Éq. (4) nous avons

Pour l'équation cubique [20, 21]

Le discriminant de l'Eq. (7) est

Paramètre \( b=-\left({\varepsilon}_L+\alpha {E}_z^2\right),\kern0.5em c=0 \), et \( d=-\alpha {\beta}^2 {H}_y^2/\left({\omega}^2{\varepsilon}_0^2\right) \), il est facile de démontrer que le discriminant de l'Eq. (6) rencontre

Δ < 0 signifie que l'Eq. (6) n'a qu'une seule vraie solution. De la méthode de Cardano [20], nous savons que pour l'équation cubique Eq. (7) sa vraie racine est

où p = c − b ² /3, q = d − bc /3 + 2b ³ /27. En utilisant l'éq. (10) on peut obtenir le ε . Remplacement du ε dans l'éq. (2) et (3) par la solution réelle, les équations différentielles ordinaires peuvent être résolues numériquement par une méthode de relaxation.

Résultats et discussions

À partir des exigences de continuité de E _z et H _y , les conditions aux limites en x = ± d /2 satisfait E _1z = E _2z et H _2y − H _1y = σ _g E _z . La conductivité de surface du graphène σ _g est régie par la formule de Kubo [22] incluant les contributions de transition interbande et intrabande. Dans la gamme de fréquences THz et infrarouge lointain, la contribution de transition intrabande domine et la conductivité de surface peut être simplifiée en un simple type Drude comme [23]

où e est la charge électronique, μ _c est le potentiel chimique du graphène, ω est la fréquence, et τ est le temps de relaxation de la quantité de mouvement. Ce modèle est applicable en limite basse température (k _B T < < μ _c ) à basse fréquence (ℏω ≤ μ _c ). Pour la condition de champ fort, la partie non linéaire de la conductivité doit être considérée et la conductivité totale du graphène se lit [16]

où E _τ est la composante tangentielle du champ électrique et σ ^NL désigne une conductivité non linéaire [16]

où ν _F = 0.95 × 10 ⁸ cm/s est la vitesse de Fermi.

Pour le graphène, ce n'est que dans la gamme de fréquences THz et infrarouge lointain que sa conductivité de surface peut être simplifiée en un simple type Drude ; par conséquent, nous choisissons la longueur d'onde incidente comme λ = 10 μm . Les autres paramètres sont fixés aux valeurs ε ₁ = 1, ε _L = 2.25, α = 5 × 10 ^− 16 (m/v) ² [24] E _F = 0,27 ev, τ = 1,5 ps. Il est bien connu qu'il existe deux modes dans les structures linéaires graphène-diélectrique-graphene, qui sont respectivement des modes symétriques et antisymétriques. Dans ce qui suit, nous discuterons de l'influence de la non-linéarité sur la distribution des modes dans les structures composites graphène-diélectriques.

Réglage H ₀ en tant que composante initiale du champ magnétique à l'interface incidente, en résolvant numériquement les équations (1, 2 et 3), la dépendance de l'intensité du champ magnétique initial H ₀ sur la constante de propagation β est donnée dans la Fig. 2. La constante de propagation normalisée \( {k}_F=\sqrt{\uppi n} \) est en unités d'impulsion de Fermi [25], où n = 6 × 10 ¹² cm ^− 2 est la densité de porteurs. Les courbes en trait plein représentent le cas où seule la non-linéarité du diélectrique est prise en compte, tandis que les courbes en pointillés indiquent le cas où la non-linéarité du diélectrique et du graphène sont prises en compte simultanément. À partir de la figure 2, nous constatons que les propriétés des modes pour les deux cas sont les mêmes. Il y a trois branches, ce qui signifie que le guide d'ondes plasmonique non linéaire peut prendre en charge trois modes. Cependant, par rapport au cas de non-linéarité unique, l'intensité du champ initial a apparemment diminué pour le cas de non-linéarité double. Bien que le guide d'ondes plasmonique non linéaire en graphène puisse prendre en charge trois modes, il est impossible de distinguer quelle branche désigne le mode symétrique, antisymétrique ou asymétrique. Afin de déterminer les propriétés de mode de chaque branche, nous traçons la distribution du champ électrique et du champ magnétique associés à A, B, C et D sur la figure 3, respectivement.

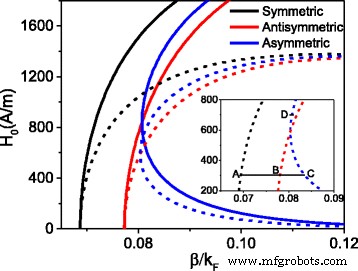
L'intensité magnétique initiale en fonction de la constante de propagation. Pour les courbes pleines :α = 5 × 10 ^− 16 (m /v ) ² , σ ^NL = 0; pour les courbes en pointillés :α = 5 × 10 ^− 16 (m /v ) ² , σ ^NL = 2.19 × 10 ^− 20 i, la ligne continue noire horizontale est une ligne auxiliaire

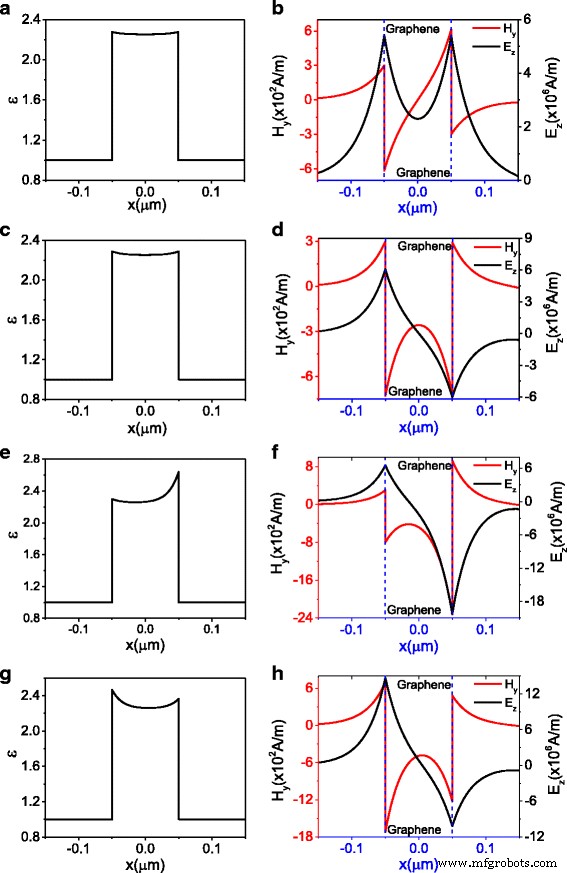
La permittivité et la distribution des modes pour la composante magnétique H _y et composant électrique E _z . un et b correspond au point A (H ₀ = 300, β = 6.94 × 10 ^− 2 k _F ) marqué sur la Fig. 2 pour les modes symétriques, c et d correspond au point B (H ₀ = 300, β = 7.81 × 10 ^− 2 k _F ) marqué sur la Fig.2 pour les modes antisymétriques, e et f correspond au point C (H ₀ = 300, β = 8.36 × 10 ^− 2 k _F ) marqué dans la Fig. 2 pour les modes asymétriques, et g et h correspond au point D (H ₀ = 700, β = 8.07 × 10 ^− 2 k _F )

Pour la branche de la courbe en pointillés noirs, la permittivité correspondante et les champs associés à A sont tracés sur la figure 3a, b, dans laquelle la distribution de la permittivité et du champ électrique E _z est symétrique. Par conséquent, cette branche représente le mode symétrique. Pour la branche de la courbe en pointillés rouges, la permittivité et les champs associés à B sont donnés sur les Fig. 3c, d. La distribution de la permittivité est toujours symétrique; cependant, la distribution du champ électrique E _z est antisymétrique ce qui implique que cette branche est un mode antisymétrique. La distribution de la permittivité et du champ associé à C et D est tracée sur la figure 3e–h. On constate que la répartition du champ magnétique et du champ électrique correspondants associés à C et D est asymétrique; par conséquent, la branche de la courbe en pointillés bleus représente le mode asymétrique. Pendant ce temps, la distribution asymétrique du champ électrique conduit à la distribution asymétrique de la permittivité.

Ensuite, nous tournons notre attention pour discuter de l'influence de la non-linéarité du diélectrique et du graphène sur la relation de dispersion. La figure 4 montre la relation de dispersion pour un champ magnétique initial fixe (H ₀ = 300 A/m) et différents potentiels chimiques et coefficients non linéaires du diélectrique. Sur la figure 4a–c, l'influence du coefficient non linéaire du diélectrique sur la relation de dispersion est montrée, où seule la non-linéarité du diélectrique est prise en compte. Lorsque le coefficient non linéaire et la conductivité non linéaire sont tous deux égaux à zéro (α = 0, σ ^NL = 0), la structure non linéaire dégénère en une structure linéaire. Sur la figure 4a, pour le cas linéaire, seuls les modes symétriques et antisymétriques existent. La courbe en trait plein noir et la courbe en trait plein rouge représentent respectivement les modes symétrique et antisymétrique. Lorsque le coefficient non linéaire est différent de zéro, un mode asymétrique comme la branche III représentée sur la figure 4b, c apparaît dans la structure. Au fur et à mesure que le coefficient non linéaire augmente, l'influence du coefficient sur les propriétés de dispersion devient faible.

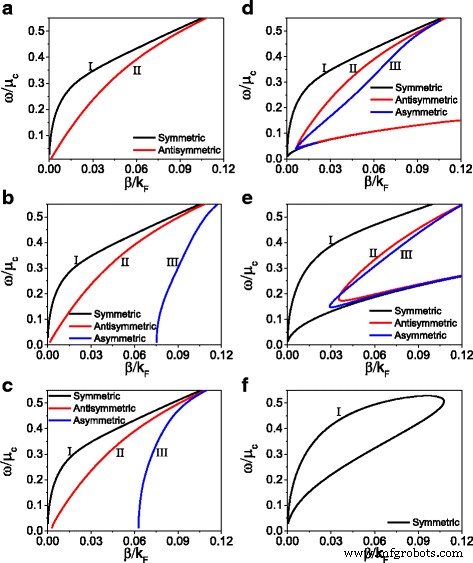
La relation de dispersion pour une intensité magnétique initiale fixe (H ₀ = 300 A/m) et pour divers coefficients non linéaires(a –c ) et pour divers potentiels chimiques (d –f ). un α = 0, μ _c = 0.27eV, σ _NL = 0, b α = 5 × 10 ^− 17 (m/V) ² , μ _c = 0.27eV, σ _NL = 0, c α = 5 × 10 ^− 16 (m/V) ² , μ _c = 0.27eV, σ _NL = 0, d μ _c = 0.27eV, α = 5 × 10 ^− 16 (m/V) ² , (e ) μ _c = 0.16eV, α = 5 × 10 ^− 16 (m/V) ² , et f μ _c = 0.10eV, α = 5 × 10 ^− 16 (m/V) ²

Dans ce qui suit, nous introduisons simultanément la non-linéarité du diélectrique et du graphène, et discutons de l'influence de la non-linéarité du graphène sur la relation de dispersion avec un coefficient non linéaire fixe du diélectrique α = 5 × 10 ^− 16 (m/V) ² . Les résultats sont présentés sur la figure 4d-f. Par rapport à la figure 4d avec la figure 4c, on remarque que le phénomène de repliement de la relation de dispersion apparaît dans les trois branches. De l'éq. (13), nous savons que la non-linéarité du graphène peut être contrôlée en ajustant le potentiel chimique. Au fur et à mesure que la non-linéarité du graphène augmente à partir de μ _c = 0.27 eV à μ _c = 0,16 eV, comme le montre la figure 4e, le point de repliement de la relation de dispersion se déplace vers le haut. Pour une plus grande non-linéarité du graphène (avec un petit potentiel chimique μ _c = 0.10eV), comme le montre la figure 4f, seul le mode symétrique apparaît et forme une boucle fermée. D'après la figure 4, nous savons qu'en ne considérant que la non-linéarité du diélectrique, la relation de dispersion montre trois branches qui sont presque immuables à mesure que le coefficient non linéaire du diélectrique augmente. Cependant, lorsque nous introduisons davantage la non-linéarité du graphène, le phénomène de repliement de la relation de dispersion apparaît. Pour le champ magnétique initial spécifié H ₀ et potentiel chimique, la relation de dispersion ne montre qu'un mode symétrique avec une boucle fermée.

Conclusions

En résumé, nous avons étudié les propriétés de mode et de dispersion du guide d'ondes plasmonique non linéaire graphène-diélectrique. La distribution des modes, la permittivité et les relations de dispersion ont été obtenues en résolvant numériquement l'équation de Maxwell pour la polarisation TM. Par rapport au cas ne considérant que la non-linéarité du diélectrique, l'intensité du champ initial a apparemment diminué lorsque l'on considère la non-linéarité du diélectrique et du graphène simultanément. De plus, la double non-linéarité affecte de manière significative les propriétés de dispersion du guide d'ondes. Surtout, à mesure que la non-linéarité du graphène augmente, les modes antisymétrique et asymétrique se confondent et disparaissent progressivement. Par conséquent, seul le mode symétrique peut être trouvé dans le cas de forte non-linéarité.