Résonance plasmon dans la photoabsorption de nanocristaux colloïdaux de ZnO fortement dopés

Contexte

Dans une large mesure, les propriétés optiques des nanoparticules sont déterminées par la présence de résonances plasmoniques de surface localisées (LSPR) dans leurs spectres d'excitation [1–8]. Kriegel et al. [2] ont publié un aperçu assez détaillé des nanocristaux colloïdaux (NC) émergents, y compris les NC d'oxydes métalliques dopés aux impuretés, les NC de chalcogénure de cuivre et les NC de semi-conducteurs dégénérés dopés, et ont longuement discuté de leurs propriétés optiques ainsi que des applications pour la détection, en champ proche amélioration de la spectroscopie, dispositifs optoélectroniques accordables ou applications biomédicales. Tous ces nouveaux matériaux sont une alternative aux métaux nobles NC qui ont été largement étudiés au cours des dernières décennies; pour un examen complet, voir également Réf. [9]. Il a été montré qu'il est possible d'ajuster la réponse optique des nanocristaux semi-conducteurs fortement dopés (NC) jusqu'à la gamme IR [10–15], en agissant sur divers paramètres de contrôle [11, 13, 16–20], ouvrant ainsi nouvelles perspectives pour la nanophotonique. Le principal avantage des NC à semi-conducteurs est que la densité de porteurs peut être réglée sur un large intervalle. Alors qu'un conducteur métallique a une densité électronique fixe, un semi-conducteur peut être dopé pour obtenir des densités de porteurs arbitraires dans une plage de 10 ¹⁶ ÷10 ²² cm ⁻³ [10, 13, 21, 22]. Le dopage des porteurs permet d'accéder au LSPR accordable dans une large gamme de fréquences allant du THz à l'IR et à la région visible [13]. Une telle accordabilité de la densité des porteurs est une propriété unique des nanoparticules semi-conductrices et ne peut pas être obtenue à l'aide de gouttelettes métalliques [23–25]. Le dopage peut être effectué en incorporant divers types d'impuretés dans le réseau cristallin [7, 10, 18], et la fréquence de résonance plasmon peut être réglée ou commutée par un contrôle actif des porteurs [13, 16-18, 21, 22]. De plus, la fréquence du plasmon et sa forme de raie dépendent non seulement de la densité de porteurs du NC mais du type de dopage, qui peut être « bulk-like » ou « surface-like » [15, 22]. Dans le premier cas, la charge de porteurs libres est neutralisée par la charge d'impuretés dopantes sur tout le volume NC, tandis que dans le second cas, les porteurs libres sont injectés dans le volume NC par des donneurs/accepteurs issus des milieux environnants situés au Interface CN.

Des études théoriques de la réponse optique des nanoparticules semi-conductrices ont révélé des différences significatives entre les descriptions de la mécanique quantique et classiques [5, 22, 24, 26]. À mesure que la taille des nanoparticules diminue, la résonance plasmon se déplace vers des énergies plus élevées avec un écart visible par rapport aux prédictions classiques [5, 21, 22]. De plus, les propriétés dynamiques des NC fortement dopées subissent une transition du régime de quantification en taille au régime classique des oscillations plasmoniques [22]. Il peut être observé en faisant varier soit le nombre de porteurs, soit la taille du CN.

Dans ce travail, nous présentons une analyse théorique de la réponse optique des NCs de ZnO photodopées telles que celles étudiées expérimentalement dans Ref. [21, 27]. Dans ces études expérimentales, les sections efficaces de photoabsorption de ZnO NC colloïdal de tailles et de densités de porteurs fixes ont été mesurées. Les photoélectrons de la bande de conduction ont été générés dans le ZnO NC par photodopage, tandis que les trous ont été piégés par les centres de piégeage des trous dans le toluène environnant. La concentration moyenne d'électrons conducteurs n _e dans des nanocristaux photodopés presque sphériques de rayons différents (de 1,75 à 6 nm) atteignait une limite supérieure de (1,4±0,4)×10 ²⁰ cm ⁻³ [21, 27]. L'absorbance intrabande a été mesurée dans la plage de 0,2 à 1,0 eV, et des différences significatives avec la prédiction du modèle Drude classique ont été observées. Les auteurs ont montré qu'une approche de mécanique quantique basée sur des transitions à une seule particule n'a donné la dépendance expérimentale de la taille de la fréquence de résonance que qualitativement [21].

L'objectif de cet article est de revisiter l'approche théorique des résonances plasmoniques dans les NCs de ZnO photodopées en dépassant l'approximation monoparticulaire sans interaction [21, 27]. Il est basé sur le traitement mécanique quantique à plusieurs corps auto-cohérent des électrons de conduction dans l'approximation de phase aléatoire (RPA) avec échange local [28]. Il a été montré que les porteurs de charge libres dans les nanoparticules semi-conductrices forment des coquilles de type atomique [29, 30]. Nous résolvons les équations de Kohn-Sham d'approximation de densité locale (LDA) pour décrire la structure de la couche électronique. Les corrélations électroniques responsables des excitations plasmoniques collectives sont prises en compte au sein du RPA. Nous montrons que la résonance plasmonique dans le ZnO NC diffère sensiblement de la résonance bien connue de Mie dans les gouttelettes métalliques. Contrairement aux NC dopés en vrac, il n'y a pas de restauration de charge positive dans le ZnO NC dopé en surface. Par conséquent, la répulsion de Coulomb entre les électrons libres les poussent près de la surface NC. À son tour, cette configuration électronique spécifique conduit à un mode dipôle, où seuls les degrés de liberté angulaires sont excités, tandis que le mouvement radial électronique n'est pas impliqué. Contrairement au plasmon dipolaire de surface de Mie ordinaire où les électrons subissent des oscillations de translation pures, les électrons des NC ZnO hautement dopés subissent des vibrations tangentielles dans la couche électronique plutôt mince d'une manière similaire aux oscillations du plasmon dans les molécules de fullerène [31]. Nous montrons également que la transition de ce mode plasmon du régime de confinement classique au régime de confinement quantique est régie par le rapport de la taille NC au rayon de Bohr effectif et ne dépend pas du nombre d'électrons libres. Les effets quantiques dans les oscillations plasmoniques entraînent un décalage vers le bleu de la fréquence de résonance du dipôle qui s'accorde bien avec la dépendance de taille LSPR observée expérimentalement [21].

Méthodes

L'objectif de l'étude est l'analyse théorique des propriétés optiques de nanocristaux de ZnO photodopés. Les configurations de l'état fondamental des systèmes avec un nombre variable de particules ont été calculées dans l'approximation de la densité locale. Les fonctions d'onde de l'état fondamental sont des énergies de particules uniques qui ont été obtenues par résolution numérique auto-cohérente de l'ensemble des équations de Kohn-Sham [32]. La base complète des états d'une seule particule a été générée en utilisant la méthode B-spline [33] en développant les fonctions de base dans une cavité de grand rayon sur un nombre fini de B-splines. Le rayon de la cavité a été choisi égal au rayon CN. La précision souhaitée des calculs avec l'utilisation de la base discrète B-spline a été obtenue par le choix approprié du nombre et de l'ordre des B-splines utilisées dans le calcul. Nous avons utilisé 50 B-splines d'ordre 7 pour obtenir une précision suffisante (10 ⁻⁵ ) des résultats. Le sous-programme standard RG du progiciel de sous-programme du système propre (EISPACK) a été utilisé pour l'obtention des valeurs propres et des vecteurs propres de l'équation matricielle RPA [28], dont la solution nous fournit l'ensemble des énergies d'excitation des dipôles et des forces d'oscillateur correspondantes. Le spectre de photoabsorption a été obtenu par l'élargissement de la distribution de force d'oscillation calculée par des profils lorentziens avec la largeur de pliage fixe.

Résultats et discussion

Structure de l'état fondamental

On considère le système de N bande de conduction électrons localisés dans le ZnO NC de rayon R . Suivant [21], nous supposons que le nombre d'électrons varie avec la taille de NC comme N =4π n _e R ³ /3, où la concentration électronique moyenne fixe, n _e =1,4×10 ²⁰ cm ⁻³ , est déterminé par le niveau le plus élevé possible dans le processus de photodopage. Le rayon des CN considérés va de 2,4 à 6 nm; en conséquence, le nombre d'électrons de conduction, N , varient de 8 à 128.

Nous utilisons l'approximation de la fonction enveloppe pour décrire le mouvement des électrons en supposant que R est beaucoup plus grande que la constante de réseau. Il est connu que la structure de bande électronique du ZnO massif est caractérisée par un spectre d'énergie non isotrope et non parabolique [34]. Cependant, pour le problème actuel de la dynamique collective de N électrons délocalisés, nous négligerons ces petits effets de spectre d'énergie et considérerons une dispersion d'énergie parabolique isotrope de masse effective \(m_{e}^{*}=0.3~m_{e}\) [34]. Pour la même raison, nous considérons les ZnO NC comme des systèmes sphériques.

Comme les électrons sont fortement localisés dans le volume ZnO NC en raison du décalage élevé de la bande de conduction à l'interface NC [6], nous imposons à toutes les fonctions d'onde électronique de disparaître à la frontière NC r =R . Ainsi, nous considérons N des électrons en interaction localisés au sein d'un puits sphérique infini dont la neutralité globale de charge est assurée par une distribution surfacique de charges positives qui ne crée aucun champ à l'intérieur du NC. L'hamiltonien effectif du système considéré est simplement :

où V (r _un ,r _b ) représente l'interaction de Coulomb d'électrons par paire. Son expression explicite, tenant compte de la polarisation du matériau ZnO et des milieux environnants, s'écrit sous la forme d'un développement multipolaire [3],

où r et r _> sont respectivement la plus petite et la plus grande des deux positions radiales. Les constantes diélectriques du ZnO et du toluène se voient attribuer leurs valeurs apparentes ε _i =3.7 et ε _m =2,25 [21], respectivement. Avec ces paramètres, le rayon de Bohr effectif \(a_{0}=\hbar ^{2} \varepsilon _{i}/m_{e}^{*} e^{2} =0.65\) nm est plus petit que le Rayon CN.

Les énergies des électrons à particule unique, ε _i , et les fonctions d'onde enveloppe ψ _i satisfaire l'ensemble des équations LDA Kohn-Sham,

où le potentiel de champ moyen V _mf est donnée par la somme des valeurs directes, V _D (r ), et échanger, V _x (r ), pièces,

avec \(\rho =\sum _{i} |\psi _{i}|^{2}\) étant la densité électronique. Notez que nous pourrions remplacer le terme d'échange dépendant de la densité locale sous sa forme Dirac par un terme d'échange-corrélation dépendant de la densité locale plus réaliste comme cela est fait habituellement. Nous ne le faisons pas car la construction théorique des états excités qui suivra automatiquement rend compte d'une grande partie des corrélations d'états fondamentaux de nature RPA.

Par souci de simplicité, nous considérons des configurations électroniques à symétrie sphérique avec des couches électroniques fermées. Dans ce cas, les fonctions d'onde à particule unique sont données comme les produits des composantes radiale, angulaire et de spin [35]. Par conséquent, l'indice i =(n ,l ), où n est le nombre quantique radial et l celui du moment cinétique. La solution numérique de l'équation. (3) pour le nombre d'électrons N <130 a montré que la configuration électronique de l'état fondamental était constituée d'états électroniques occupés avec les nombres quantiques radiaux les plus bas n =1. Ces états électroniques ont des fonctions d'onde radiales sans nœud et diffèrent par les valeurs des moments angulaires l . Ainsi, compte tenu de la dégénérescence du spin, les nombres « magiques » d'électrons pour de telles configurations symétriques sont N =2(l _max +1) ² , où l _max est le moment cinétique maximal de l'état électronique occupé le plus élevé. Sur la figure 1, nous montrons les distributions de densité ρ (r ) pour la CN avec N =18, 50, 128 électrons. On peut voir que la distribution de densité radiale devient de plus en plus étroite et se déplace vers l'interface NC à mesure que la taille augmente. L'insert de la figure 1 montre la dépendance de la taille de la valeur électronique moyenne de la distribution radiale électronique 〈r 〉 sur le rayon NC R et le rapport δ r /R , de sa dispersion \(\delta r =\sqrt {\langle r^{2} \rangle - {\langle r\rangle }^{2}}\) (qui peut être considérée comme la largeur effective de la coque électronique) à le rayon CN. Ce rapport qui ne s'élève que 0,15 pour le plus petit NC avec N =8 électrons diminue rapidement pour les systèmes plus grands. Numériquement, la largeur de la coque électronique δ r est d'environ les deux tiers du rayon de Bohr effectif a ₀ alors que le pic de la coque électronique est décalé de l'interface NC en raison de la réflexion quantique d'environ R −〈r 〉≃2a ₀ . Cette caractéristique du système électronique découle de la forte répulsion de Coulomb qui pousse les électrons vers la frontière NC formant une distribution de charge sphérique creuse. Si le rayon NC est suffisamment grand, la force de répulsion de Coulomb à la frontière NC e ² N /ε _i R ² devient beaucoup plus forte que la force centrifuge \(\hbar ^{2}l(l+1)/m_{e}^{*}{\langle r \rangle }^{3}\) même pour l'état occupé le plus élevé avec \(l=l_{max}=\sqrt {N/2}-1\). On peut voir que leur ratio s'élève à a ₀ /2R . C'est pourquoi les mouvements radiaux et angulaires des électrons se séparent si R ≫a ₀ . Dans ce cas, le système électronique est similaire à un rotateur quantique, par exemple, le spectre d'énergie des états à particule unique occupés ε _i de l'éq. (3) est bien approximé par la formule,

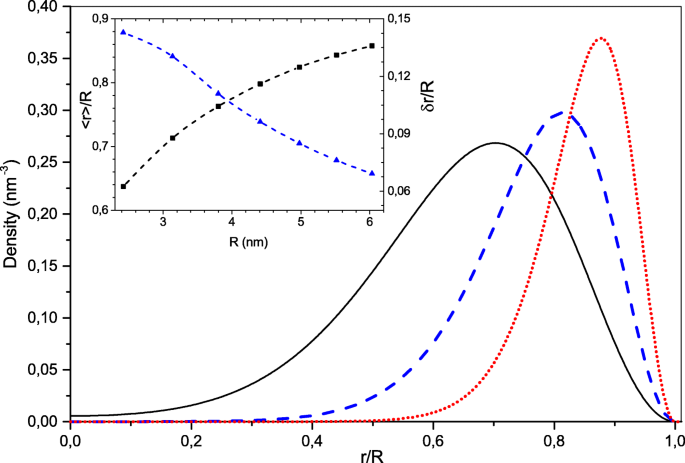
Distributions de densité radiale pour les CN avec différents nombres d'électrons délocalisés, N =18 (ligne noire continue), 50 (ligne bleue pointillée), 128 (ligne rouge pointillée). En encadré, le rayon moyen réduit (noir) et sa dispersion (bleu) est représenté en fonction du rayon NC

Réponse optique

Dans l'approximation de la réponse linéaire, un champ électrique harmonique externe induit des champs auto-cohérents dépendant du temps de même fréquence. La connaissance des vibrations de faible amplitude correspondantes renseigne sur les états excités dipolaires ainsi que sur les probabilités de transition entre l'état fondamental et les états excités. Pour un système dont l'état fondamental est un déterminant de Slater |Φ ₀>, les états excités dipôles à N corps corrélés dans l'approche RPA sont construits comme une superposition linéaire d'une excitation particule-trou [36] :

. $$ (6)

Les indices i ,m , (j ,n ) se référer aux états monoparticulaires au-dessus (au-dessous) du niveau de Fermi F ; \(\hat {a}^{+}\) et \(\hat {a}\) sont respectivement les opérateurs de création et de destruction de particule unique.

Les amplitudes vers l'avant, \(X_{ij}^{\nu }\), et vers l'arrière, \(Y_{ij}^{\nu }\), peuvent être obtenues en résolvant l'équation RPA matricielle [ 28] :

$$ \left(\begin{array}{ll} \mathbf{A} &\mathbf{B} \\ \mathbf{B}^{\star} &\mathbf{A}^{\star} \end{ array} \right) \left(\begin{array}{l} \mathbf{X}^{\nu} \\ \mathbf{Y}^{\nu} \end{array} \right) =\omega_{ \nu} \left(\begin{array}{l} \mathbf{X}^{\nu} \\ -\mathbf{Y}^{\nu} \end{array} \right), $$ (7 )

où les valeurs propres ω _ν sont les énergies d'excitation. Les matrices A et B sont définis comme suit

$$ {\begin{aligned} A_{ij,mn}&\,=\,\delta_{im}\delta_{jn}\left(\varepsilon_{i}-\varepsilon_{j}\right) \,+ \, \left\langle in\left| \hat{v}\right| jm\right\rangle, \quad B_{ij,mn}&\,=\,\left\langle im\left| \hat{v}\right| jn\right\rangle \\ \hat{v}(\mathbf{r},\mathbf{r}^{\prime}) &=V(\mathbf{r},\mathbf{r}^{\prime} )+ \delta\left(\mathbf{r}- \mathbf{r}^{\prime}\right)\delta V_{x}/\delta \rho. \end{aligné}} $$ (8)

Notons au passage que les amplitudes arrière, \(Y_{ij}^{\nu }\), mesurent la contribution des corrélations d'état fondamental électron-trou \(\hat {a}_{j}^{+}\hat { a}_{i}|\Phi _{0}>\), respectivement, à l'excitation de l'état excité |Φ _ν > de fréquence ω _ν .

Les forces correspondantes de l'oscillateur dipolaire f _ν sont exprimés en termes d'amplitudes RPA X ^ν et O ^ν ,

$$ f_{\nu} =\frac{2 m_{e}^{*} D^{2}_{\nu}\omega_{\nu}}{\hbar^{2}}, \quad D_{ \nu} =\sum_{ij} \left(X^{(\nu)}_{ij} d_{ij} + Y^{(\nu)}_{ij} d_{ji} \right), $ $ (9)

où d _ij =〈i |z |j 〉 sont les éléments de la matrice dipolaire à particule unique.

Les sections efficaces de photoabsorption ont été obtenues en élargissant la distribution de force d'oscillateur calculée par des profils lorentziens avec la largeur de pliage de 0,2 ω . Spectres de photoabsorption avec distributions de force d'oscillateur pour les CN avec N =8 (a), 32 (b), 50 (c) et 128 (d) électrons sont représentés sur la figure 2. Sur la figure 2d, nous comparons la section efficace de photoabsorption calculée avec les données expérimentales de la réf. [21] pour ZnO NC avec R 6 nm. On peut voir que dans toutes les CN considérées, les spectres sont dominés par une seule raie de résonance, dont la position détermine en fait le maximum de la section efficace de photoabsorption. En effet, cela est attendu puisque le spectre électronique d'une particule est similaire à un rotateur quantique. Les transitions les plus fortes se produisent pour une fonction d'onde maximale se chevauchant, c'est-à-dire avec un nombre quantique radial égal n . Dans notre cas, il n'y a qu'une seule transition optique depuis l'état occupé le plus élevé j =(1,l _max ) à l'état vacant le plus bas i =(1,l _max +1). Cependant, l'excitation dipolaire correspondante diffère fortement de la transition à particule unique sans interaction chaque fois qu'une forte répulsion de Coulomb rend les corrélations électroniques importantes et écrasantes. C'est le cas lorsque R ≫a ₀ . A savoir, l'énergie d'excitation collective, ω _ν , dépasse l'énergie de transition monoparticulaire

$$ \Delta =\left(\epsilon_{1, l_{max}+1} -\epsilon_{1, l_{max}}\right)=\frac{\hbar^{2} (l_{max}+ 1)}{m_{e}^{*}{\langle r \rangle}^{2}}. $$ (10)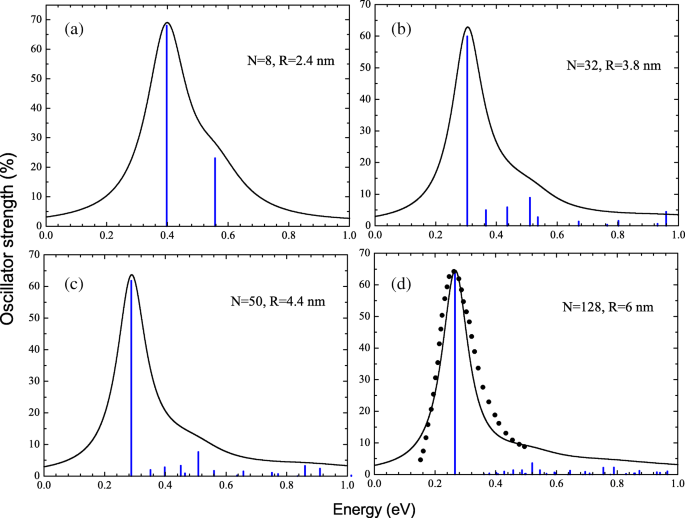

Distributions de force d'oscillateur et profils de pic de photoabsorption correspondants calculés dans l'approche RPAE pour les CN avec N =8 (a ), 32 (b ), 50 (c ) et 128 (d ) électrons de la bande de conduction. Comparaison des profils de pic de résonance expérimentaux [21] (carrés noirs) et calculés (trait plein) pour NC avec R ≈6 nm (d )

Sur la figure 3, nous comparons les positions des maxima de photoabsorption, ω _res , calculé ici (cercles bleus) avec les résultats expérimentaux de [21] (étoiles rouges). On observe une concordance remarquable entre les données expérimentales et nos résultats théoriques. A titre de comparaison, nous traçons également ici les énergies Δ de transition monoparticulaire (carrés verts). Les corrélations électroniques augmentent considérablement l'énergie d'excitation collective comparativement à Δ . Une simple analyse de RPA Eq. (7) explique cette observation. Si l'on ne considère que la transition optique principale de j =(1,l _max ) à j =(1,l _max +1), le RPA Eq. (7) se réduit à une équation matricielle 2×2, dont la valeur propre ω est simplement :

$$ \omega^{2}=\Delta^{2} +2V\Delta, $$ (11)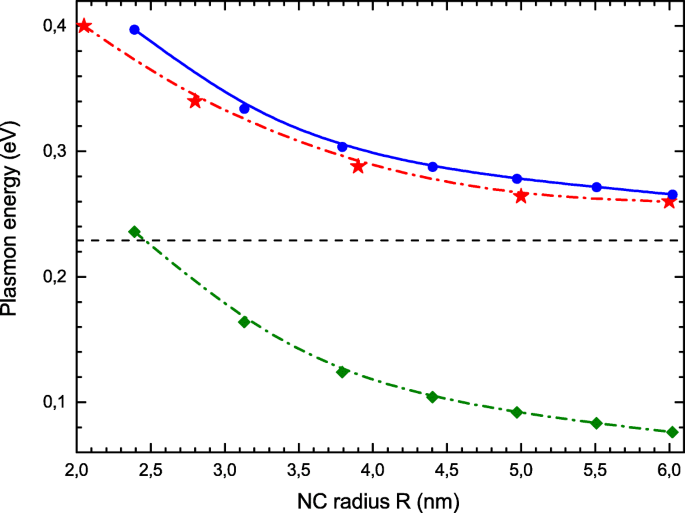

Dépendance de taille de l'énergie LSPR. Valeurs expérimentales [21] (étoiles rouges), RPA avec échange local (cercles bleus), énergies de transition monoparticulaire (losanges verts dans la courbe inférieure). La valeur classique (13) est indiquée par la ligne pointillée horizontale

où \(V=\left \langle ij\left | \hat {v}\right | ij\right \rangle \) désigne l'élément de matrice RPA Coulomb. Le premier terme de la droite à droite. de l'éq. (11) donne la contribution de la particule unique tandis que le second terme résulte des interactions particule-trou. Leur rapport peut être estimé en prenant la coordonnée radiale de l'électron à la surface, r =R dans l'élément de matrice RPA V , et en négligeant le terme d'échange. Cette estimation donne

$$ \frac{2V}{\Delta} \simeq \frac{4R\varepsilon_{i}}{a_{0}(\varepsilon_{i}+2\varepsilon_{m})} \simeq \frac{2R} {a_{0}}. $$ (12)

Ainsi, la contribution des corrélations électroniques domine si R ≫a ₀ . Dans la limite des grands CN, la distribution de la densité électronique est concentrée à la surface du CN; par conséquent, selon l'Éq. (12), l'énergie de résonance dans l'équation. (11) a tendance à

$$ \omega =\sqrt{\frac{2\hbar^{2}e^{2}N}{m_{e}^{*}(\varepsilon_{i}+2\varepsilon_{m})R^ {3}}}, $$ (13)

ce qui coïncide exactement avec la fréquence classique du plasmon dipolaire dans une couche sphérique mince [37]. Ce mode plasmon correspond à une vibration électronique tangentielle. De cette façon, il est similaire à la résonance plasmonique de surface dans C ₆₀ molécules, où la fréquence de résonance est bien décrite par l'équation analogue à l'Eq. (13) [38]. A noter que comme le cas du fullerène [39], ce mode plasmon rassemble les deux tiers de la force d'oscillation totale (voir Fig. 2). Cela se produit parce que cette oscillation n'implique que les degrés de liberté angulaires, gardant le mouvement radial non perturbé.

Contrairement au mode bien connu du plasmon de surface dipolaire dans les sphères homogènes, qui est purement translationnel, le mode considéré ici est compressionnel. La densité induite produit un champ électrique parallèle à la surface qui joue le rôle de force de rappel pour ce mode plasmon. De plus, la variation purement quantique du niveau de Fermi local due aux oscillations de densité induites contribue à la force de rappel. La contribution de la pression quantique correspondante à la fréquence de résonance est donnée par le Δ terme dans l'éq. (11). Il est plus petit que la contribution de Coulomb dans tous les CN considérés en raison de la petitesse du rayon de Bohr effectif a ₀ en ZnO. Cependant, dans les CN avec une valeur plus élevée de a ₀ , on a pu observer la transition de la résonance plasmonique dipolaire classique au régime de confinement quantique à R ∼a ₀ . Il est à noter que dans le cas des NC dopés, le paramètre a ₀ /R qui contrôle la nature classique/quantique de la résonance dipolaire ne dépend que de la taille NC et ne dépend pas du nombre de porteuses libres N .

Sur la figure 3, la ligne horizontale fait référence à l'énergie de résonance plasmonique classique (13). Le décalage vers le bleu de la fréquence de résonance par rapport à sa valeur classique est causé par deux effets quantiques, la contribution de la pression quantique discutée ci-dessus et la diminution du rayon moyen des électrons. Ce dernier se produit parce que les électrons sont poussés dans le volume NC en raison de la réflexion quantique de la frontière, de sorte que 〈r 〉≃R -2a ₀ . Cet effet augmente l'élément de matrice V qui à son tour augmente la fréquence de résonance. En gros, cet effet peut être reproduit en remplaçant le rayon CN R au dénominateur de l'éq. (13) par 〈r . Selon les équations. (11)–(13), les deux effets fournissent le décalage de fréquence bleu proportionnel au rayon NC inverse ∝1/R . Cependant, numériquement, la contribution du dernier est la plus importante.

Conclusions

Pour conclure cette lettre, nous avons élaboré une théorie qui prédit bien la forte résonance dipolaire observée dans les ZnO colloïdaux fortement dopés n. Le nouveau type d'excitations plasmoniques dipolaires de surface a été théoriquement étudié en utilisant une approche quantique à N corps. Nous avons démontré que la forte répulsion coulombienne dans les nanocristaux de ZnO photodopé conduit à une distribution électronique spécifique à l'état fondamental localisée dans une fine couche superficielle proche de la surface interne. Lorsque le dipôle est excité, cette distribution électronique entretient une oscillation plasmonique collective qui est essentiellement formée de mouvement angulaire. La transition de ce mode de plasmon de surface du régime de confinement classique au régime de confinement quantique est régie par un seul paramètre égal au rapport de la taille du nanocristal au rayon de Bohr effectif. La réflexion des électrons de l'interface NC réduit le rayon de la coque électronique. De plus, la variation du niveau de Fermi local apporte une contribution supplémentaire à la force de rappel de l'oscillateur plasmon. Ces effets quantiques conduisent à la dépendance en taille de la fréquence des plasmons de résonance, ce qui est un accord remarquable avec les observations expérimentales. Dans la limite du grand rayon NC, la ligne de résonance tend doucement vers la fréquence plasmon classique d'une couche chargée de largeur infinitésimale.

Abréviations

LDA :

Approximation de la densité locale

LSPR :

Résonance plasmonique de surface localisée

NC :

Nanocristal

RPA :

Approximation de phase aléatoire