Effet de contrainte sur les performances thermoélectriques de la monocouche InSe

Introduction

Les matériaux semi-conducteurs bidimensionnels (2D) ont attiré l'attention des chercheurs pour explorer leurs propriétés fascinantes et leurs applications utiles depuis la découverte du graphène. En particulier, la famille des chalcogénures métalliques bidimensionnels s'est avérée présenter un grand potentiel en nanoélectronique et en nanophotonique en raison de leurs propriétés électroniques, optiques et mécaniques extraordinaires [1,2,3,4]. Récemment, le séléniure d'indium (InSe), un composé de métal-chalcogénure en couches du groupe III-VI, est d'un grand intérêt à la fois expérimentalement et théoriquement. Il a été rapporté que la couche atomique d'InSe a été synthétisée avec succès via des méthodes physiques [5,6,7,8,9,10] et chimiques [11,12,13,14], et les applications de nanofeuillet d'InSe sur des capteurs [15] , l'optoélectronique et les photodétecteurs ont été explorés. Srinivasa et al. ont rapporté la fabrication de photodétecteurs InSe à quelques couches avec une haute réactivité et une large détection spectrale du visible au proche infrarouge [6]. Bandurine et al. ont trouvé un gaz d'électrons bidimensionnel de haute qualité dans un InSe à quelques couches avec des mobilités de porteurs de 10 ³ et 10 ⁴ cm ² /Vs à température ambiante et hélium liquide [16]. Wei et al. découvert que les FET multicouches InSe à porte arrière présentent une mobilité de porteur ultra-élevée jusqu'à 1 055 cm ² /Vs à température ambiante en raison de la suppression de la diffusion des porteurs du substrat diélectrique [5].

L'InSe 2D a une structure de bande assez inhabituelle, qui est la combinaison d'une bande plate en haut de la bande de valence et d'une bande parabolique en bas de la bande de conduction, présentant ainsi des caractéristiques thermoélectriques élevées [17]. En particulier, les performances thermoélectriques peuvent être décrites par la figure de mérite non dimensionnée, ZT , défini comme ZT =S ² Tσ/ (Κ _e + Κ _l ), où S est le Seebeck efficace, T est la température absolue, σ est la conductivité électrique, et Κ _e et le Κ _l sont la conductivité thermique avec les contributions des porteurs électroniques et du réseau, respectivement. La conductivité thermique du réseau K _l pertinent à la propriété de transport des phonons joue un rôle important pour déterminer les performances thermoélectriques. Le précédent signalé K _l de la monocouche d'InSe est bien inférieure à celle du graphène, alors qu'elle était 10 fois supérieure à celle de la feuille de SnSe [18, 19].

Le niveau élevé de mobilité des électrons et la faible conductivité thermique sont bénéfiques pour les performances thermoélectriques. En outre, l'InSe monocouche présente une flexibilité mécanique supérieure et les propriétés électroniques peuvent être modulées en continu par une contrainte modérée dans une large gamme [20,21,22]. Il a été démontré que le facteur de puissance thermoélectrique de l'InSe monocouche peut être significativement amélioré par la convergence des bandes sous une contrainte de compression [23]. Pour les matériaux thermoélectriques, la déformation en traction peut également induire une variation de la structure de la bande et des propriétés de transport thermique. Cependant, la dépendance des propriétés de transport thermique sur la déformation est imprévisible, étroitement liée au matériau particulier et à la structure cristalline. Dans cet article, le présent travail est effectué sur l'effet de contrainte de traction biaxiale pour les performances thermoélectriques de la monocouche d'InSe par des calculs de premiers principes, y compris les propriétés de transport électronique et de phonons. En raison de la diffusion anharmonique accrue, l'effet positif de la contrainte de traction sur les performances thermoélectriques de la monocouche d'InSe est déterminé.

Méthodologie

Le calcul des propriétés structurelles et électroniques de la monocouche d'InSe est effectué sur la base de la théorie de la fonctionnelle de la densité (DFT) telle que implémentée dans le package de simulation ab initio de Vienne (VASP) [24,25,26]. Nous avons choisi la méthode des ondes augmentées par projecteur avec l'approximation de la densité locale (LDA) [27,28,29] pour la fonctionnelle d'échange-corrélation. Et 12 Å de vide le long du z -axis est utilisé pour éviter l'interaction entre les images périodiques des dalles. Les maillages k 21 × 21 × 1 et 31 × 31 × 1 Monkhorst-Pack ont ​​été utilisés lors des calculs de relaxation structurelle et de structure électronique pour la cellule unitaire. La coupure d'énergie de la base d'onde plane a été fixée à 500 eV. Le critère de convergence pour une énergie totale a été fixé à 10 ⁻⁴ eV, et toutes les positions atomiques et structures de réseau étaient complètement relâchées avec une tolérance de force de 10 ⁻³ eV/Å.

Les propriétés de transport thermoélectrique peuvent être obtenues dans l'approximation à temps de relaxation constant par la théorie de Boltzmann telle qu'implémentée dans le programme BoltzTraP [30, 31]. Dans cette approximation, les coefficients de transport électronique peuvent être donnés par

où est le volume de la maille unitaire, f _μ est la fonction de distribution de Fermi-Dirac, et α et β sont des indices tenseurs. La fonction de distribution des transports ∑_αβ (ε ) est donné par

où N ₀ indique le nombre de q points échantillonnés, i est l'indice de bande, v est la vitesse de groupe des porteurs, et τ est le temps de relaxation.

Le package ShengBTE [32] est utilisé pour résoudre l'équation de transport du phonon Boltzmann et déterminer la thermique du réseau et d'autres paramètres pertinents. Une supercellule 5 × 5 × 1 est utilisée pour calculer les constantes de force interatomiques harmoniques en utilisant le calcul de la théorie des perturbations fonctionnelles de la densité (DFPT) [33]. Et la méthode des différences finies est utilisée pour calculer les constantes de force interatomiques anharmoniques avec une supercellule 4 × 4 × 1 [34]. Le spectre de phonons a été calculé en utilisant le programme Phonopy [35].

Résultat et discussion

La monocouche InSe est une feuille atomique quadruple avec une liaison covalente Se-In-In-Se en une seule couche. En vue de dessus, la monocouche présente un réseau en nid d'abeille et chaque atome de Se est lié à trois autres atomes d'In, comme le montre la figure 1a. Sur la base de la minimisation de l'énergie totale, les paramètres de maille de ce cristal sont calculés pour être a ₀ =3,95 . Dans cet article, nous employons la déformation biaxiale sur la monocouche InSe en maintenant la symétrie cristalline en changeant ses réseaux comme δ =(un −un ₀ )/a ₀ × 100 %, où a et un ₀ sont la constante de réseau de la monocouche InSe avec déformation et sans déformation, respectivement. Lorsque la contrainte de traction biaxiale est imposée sur la monocouche InSe, la longueur de liaison d _InSe augmente de façon monotone avec l'augmentation de la contrainte, ce qui conduit à l'augmentation de l'angle de liaison de In-Se-In (voir Fig. 1b).

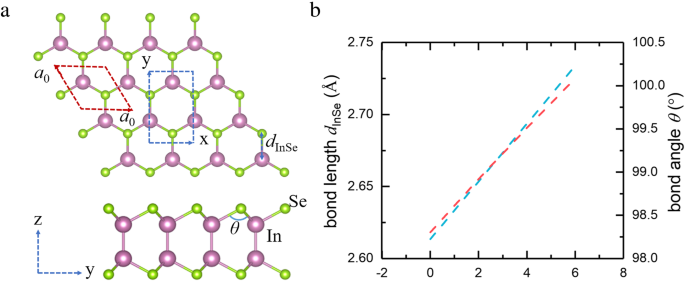
un Vue de dessus et vue de côté de l'InSe monocouche. Les boules roses et vertes représentent respectivement les atomes In et Se. b La variation de la longueur de liaison et de l'angle de liaison avec l'augmentation de la contrainte de traction biaxiale. Le a de base ₀ × a ₀ cellule unitaire et x × y les supercellules de la monocouche d'InSe sont désignées par des lignes pointillées rouges et bleues, respectivement

La monocouche d'InSe présente un semi-conducteur indirect avec une bande interdite de 1,67 eV, où le minimum de bande de conduction (CBM) existe sur le point et les sites maximum de bande de valence (VBM) entre les points Г et K, comme le montre la figure 2a. La bande de valence de la monocouche d'InSe présente une dispersion en chapeau mexicain, qui peut également être trouvée dans de nombreux matériaux bidimensionnels [36,37,38,39]. La modification de la structure de la bande en réponse à la contrainte de traction a été étudiée sur la figure 2, et les trois extrema de la bande de conduction sont désignés par les symboles I, II et III respectivement. Sous une contrainte de traction, la bande de conduction de plus basse énergie est sensible à la contrainte et se déplace vers le bas, tandis que la bande de valence reste presque constante, entraînant la réduction de la bande interdite. Sans contrainte, il existe des différences minimes entre le minimum de la deuxième et de la troisième bande de conduction, et les vallées de la bande ont tendance à converger. Cependant, avec l'augmentation de la contrainte de traction, la différence d'énergie augmente progressivement. Nous avons également comparé les bandes interdites sous différentes contraintes avec les résultats théoriques et expérimentaux connexes, comme détaillé dans le fichier supplémentaire 1 :tableau S2.

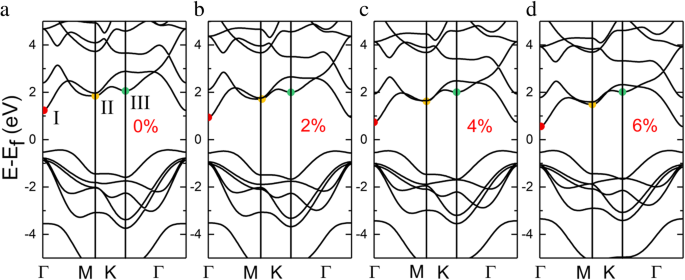
Structure de bande de la monocouche d'InSe sous différentes conditions de déformation

Effet de la contrainte de traction sur les coefficients de transport thermoélectrique

Sur la base de la structure électronique calculée, nous effectuons des calculs de coefficient de transport thermoélectrique par la théorie semi-classique de Boltzmann. En ce qui concerne le temps de diffusion τ , coefficient de Seebeck S , et la conductivité électrique σ peut être calculé. La figure 3a montre le coefficient Seebeck calculé en fonction du niveau de Fermi. Pour simplifier, la structure de la bande est souvent supposée rester inchangée par rapport au dopage à des températures finies [40, 41], et l'effet de dopage sur le coefficient de transport thermoélectrique peut être obtenu par la variation de la position du niveau de Fermi. Un ε négatif _f indique un dopage de type p en déplaçant le niveau de Fermi dans la bande de valence, et le coefficient Seebeck positif peut être obtenu. De même, un ε positif _f a donné un coefficient de Seebeck négatif. On peut trouver que le résultat obtenu sans déformation est très proche du rapport précédent [17], et le maximum du coefficient de Seebeck diminue avec l'augmentation de la déformation en traction, ce qui est lié au changement de la bande interdite [42].

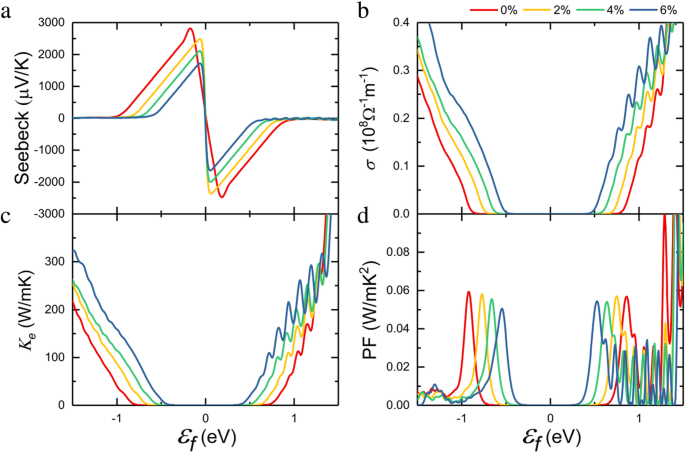
un Coefficient de Seebeck, b conductivité électrique, c conductivité thermique électronique, d facteur de puissance de la monocouche InSe en fonction du potentiel chimique à 300 K lorsque les différentes déformations biaxiales sont appliquées

Pour calculer la conductivité électrique σ , temps de relaxation τ est requis car la sortie est σ /τ dans le code BoltzTraP. Par la présente, τ est déterminé par

où μ est la mobilité des transporteurs et m * est la masse effective. Dans la théorie du potentiel de déformation, la mobilité des porteurs dans les matériaux 2D peut être calculée par [43, 44]

Ici, e est la charge électronique, est la constante de Planck et k _B est la constante de Boltzmann. C représente le module d'élasticité et peut être calculé par C = (∂ ² E /∂δ ² )/S ₀ , où E , δ , et S ₀ sont l'énergie totale, la déformation appliquée et la zone à l'équilibre pour le système 2D, respectivement. E ₁ est la constante de potentiel de déformation indiquée par E ₁ = ΔE _bord /Δδ , où ΔE _bord est la variation d'énergie des bords de bande. m _d est la masse effective moyenne dérivée de \( {m}_d=\sqrt{m_x^{\ast }{m}_y^{\ast }} \). Afin de calculer la mobilité, un x rectangulaire × y supercell est adopté comme le montre la figure 1a. La valeur obtenue de C le long de x (y ) est de 60,43 N/m (53,68 N/m), qui est obtenu en ajustant la courbe de la relation énergie-déformation, comme indiqué dans le fichier supplémentaire 1 :Figure S1. Le potentiel de déformation calculé E ₁ est de 6,13 eV (6,14 eV) pour l'électron le long de x (y ) direction, et 3,45 eV (3,33 eV) pour le trou le long de x (y ) direction. Les résultats calculés de la masse effective, de la mobilité des porteurs et du temps de relaxation pour la monocouche InSe sous différentes contraintes sont résumés dans le tableau 1. Nous pouvons trouver cette petite différence avec différentes directions, et la masse effective et la mobilité du porteur sont généralement isotropes. Par conséquent, nous utilisons la valeur moyenne de x et y instructions pour évaluer les performances thermoélectriques plus tard. Les masses effectives des trous sont améliorées par la contrainte appliquée tandis que les masses effectives des électrons restent presque inchangées. Avec le temps de relaxation calculé, la conductivité électrique peut être obtenue à un potentiel chimique donné sur la figure 3b. On peut voir que la conductivité électrique σ augmente avec l'augmentation de la contrainte de traction dans un système dopé lourd de type p en raison de l'amélioration de la mobilité des trous, alors que σ reste relativement faible à faible niveau de dopage. De plus, la tendance de la conductivité thermique électronique suit la conductivité électrique grâce à la loi de Wiedemann-Franz :K _e =LσT dans la figure 3c, où L est le nombre de Lorenz. Le facteur de puissance peut être obtenu par PF =S ² σ /τ , qui détermine la quantité d'électricité pouvant être produite. Compte tenu de la tendance globale du coefficient Seebeck et de la conductivité électrique, la contrainte de traction réduit légèrement le facteur de puissance, comme observé sur la figure 3d.

Effet de la contrainte de traction sur Κ _l

Dans les métaux, les électrons sont responsables des caloporteurs, tandis que dans les semi-conducteurs et les solides diélectriques où le dopage et la température ne sont pas très élevés, les vibrations du réseau seront la principale raison du transport d'énergie [45]. La conductivité thermique du réseau est un paramètre très important pour les applications thermoélectriques. Du point de vue théorique et comme une simple approximation, la conductivité thermique du réseau Κ _l peut être exprimé comme suit [46,47,48] :

où C _λ , v _λ , et V sont respectivement la contribution de la chaleur spécifique, la vitesse du groupe des phonons et le volume cristallin. τ _λ est le temps de relaxation du mode λ, qui peut être estimé à l'aide de la règle de Matthiessen [49] :

où \( \frac{1}{\tau_{\uplambda}^b} \)est le taux de diffusion aux limites, \( \frac{1}{\tau_{\uplambda}^{\mathrm{iso}}} \ )est le taux de diffusion isotrope des impuretés, et \( \kern0.1em \frac{1}{\tau_{\uplambda}^{3\mathrm{ph}}} \) est le taux de diffusion à trois phonons.

La figure 4a présente Κ _l variation de l'InSe monocouche avec la température sous différentes déformations. La conductivité thermique du réseau dans le cas sans contrainte est de 25,9 W/mK à température ambiante, ce qui est comparable au rapport précédent [19]. Lorsque la déformation appliquée est augmentée à 6 %, la conductivité thermique du réseau diminue à 13,1 W/mK, ce qui confirme que l'ingénierie des déformations est une méthode très efficace pour modifier la conductivité thermique du réseau. Nous traçons la courbe de dispersion des phonons correspondante de la monocouche d'InSe pour différentes contraintes sur la figure 4c, afin de déterminer l'origine de la réduction de la conductivité thermique du réseau. Il contient 12 modes de phonons car la monocouche InSe a une cellule unitaire à quatre atomes. Il n'y a pas de fréquence négative dans les spectres de phonons, ce qui confirme que la monocouche d'InSe est thermiquement stable. Trois branches à partir de 0 dans la région de basse énergie de la courbe de dispersion des phonons sont z -axe acoustique (ZA), acoustique longitudinal (LA) et acoustique transverse (TA), respectivement, et les autres sont des modes optiques. Avec l'augmentation de la contrainte de traction, la nature quadratique du mode ZA se transforme en une ligne presque droite dans la région de basse énergie. La tendance à la baisse de la fréquence des modes optiques peut être observée sous contrainte de traction, car la contrainte de traction affaiblit les liaisons et conduit alors à des fréquences plus basses. Nous discutons également de la contribution de chaque branche de phonon vers Κ _l pour la monocouche InSe non contrainte et à déformation de 6 % sur la figure 4b. Pour la condition sans déformation, le mode ZA contribue de manière significative à transporter la chaleur, et lorsqu'une déformation de traction de 6 % est appliquée à la monocouche InSe, la contribution relative du mode ZA est réduite de 58 à 38 %. Au fur et à mesure que la contrainte de traction augmente, le mode ZA devient plus dur, entraînant une diminution de la contribution à Κ _l .

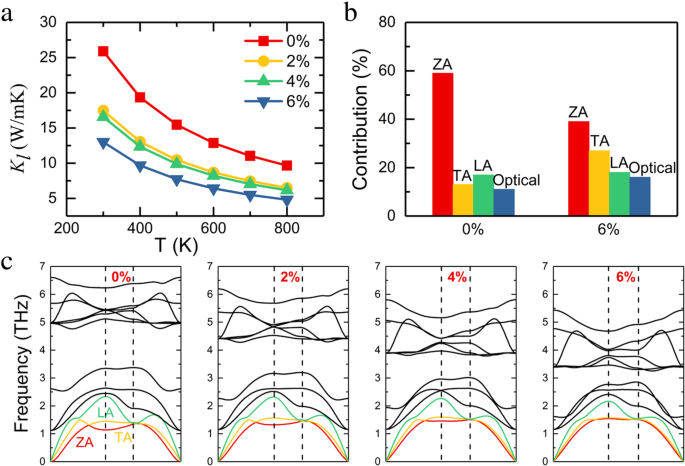
un Calcul des effets de la déformation biaxiale sur la conductivité thermique du réseau à différentes températures. b Contribution du ZA, TA, LA et de toutes les branches optiques à la conductivité thermique du réseau pour les systèmes non contraints et 6% contraints. c Les courbes de dispersion des phonons de l'InSe monocouche pour différentes déformations

Ensuite, une analyse détaillée de la variation de vitesse de groupe de phonons induite par la contrainte de traction est présentée pour comprendre les propriétés de transport des phonons. Pour les modes acoustiques dans le plan, les vitesses des groupes de phonons sont diminuées à la déformation de 6 %, comme le montrent les figures 5a, b. Combinée à la contribution accrue de LA et TA, la diminution de la vitesse du groupe de phonons joue un rôle essentiel dans la réduction de Κ _l . Le changement des vitesses de groupe de phonons provient de la variation de structure induite par la déformation :lorsque la déformation de traction est activée, la distance de liaison augmente et la force de liaison diminue, entraînant une fréquence de phonon et une vitesse de groupe inférieures. Considérant que trois branches de phonons acoustiques contribuent principalement à Κ _l , les vitesses de groupe de phonons accrues des branches optiques ont un effet limité.

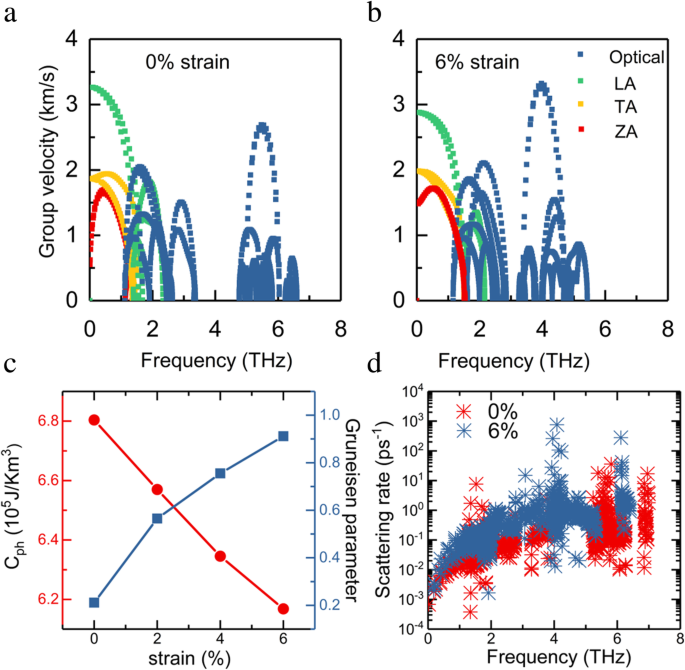
La contribution des modes ZA, TA, LA et optique à la vitesse de groupe de la monocouche InSe pour (a ) sans contrainte et (b ) 6% systèmes tendus. c Capacité calorifique du phonon (C _ph ) et paramètre de Gruneisen en fonction de la déformation à 300 K. d Taux de diffusion des phonons de l'InSe monocouche non contraint et 6% contraint en fonction de la fréquence.

Le taux de diffusion à trois phonons de l'InSe monocouche sans et avec une déformation de 6 % en fonction de la fréquence est représenté sur la figure 5d. On peut observer que le taux de diffusion à trois phonons de l'InSe monocouche contraint à 6 % dans la région des fréquences inférieures est significativement plus élevé que celui du cas non contraint, ce qui indique que l'augmentation de la contrainte donne lieu à une diffusion à trois phonons plus forte. La diffusion améliorée à trois phonons est principalement responsable de la conductivité thermique réduite du réseau, ce qui est également cohérent avec la conclusion précédente [19]. Une tendance similaire du taux de diffusion des phonons avec l'augmentation de la contrainte de traction a été observée dans ZrS₂ et 2H MoTe₂ monocouche [50, 51]. Nous avons également analysé l'effet de la contrainte de traction biaxiale sur la capacité thermique des phonons (C _ph ), comme le montre la figure 5c. Avec l'augmentation de la déformation en traction, la capacité thermique des phonons de la monocouche d'InSe est diminuée de manière monotone. Pour le système contraint à 6 %, la capacité calorifique des phonons est réduite à 6,2 × 10 ⁵ J/Km ³ . En raison de la linéarisation et du raidissement du mode ZA, la densité d'états de phonons est diminuée, ce qui conduit à une capacité thermique réduite des phonons. Les paramètres de Gruneisen fournissent des informations sur l'anharmonicité d'un système et peuvent être obtenus à partir des constantes de force interatomiques anharmoniques (IFC) [32, 52]. La figure 5c affiche les paramètres de Gruneisen calculés sous différentes contraintes. L'augmentation du paramètre Gruneisen induite par la contrainte de traction signifie une anharmonicité plus forte, conduisant à une conductivité thermique plus faible [18].

Avec toutes les propriétés de transport thermoélectrique disponibles, la figure de mérite, ZT, peut être obtenue. La contrainte de traction appliquée a un effet différent sur ces propriétés de transport, et l'amélioration des performances thermoélectriques de la monocouche InSe nécessite un équilibre compliqué entre ces paramètres S , σ , et κ . La figure 6 affiche le facteur de mérite calculé avec différentes souches en fonction du potentiel chimique à 300 K, et il est évident que la variation de la valeur ZT sous différentes souches dépend fortement du potentiel chimique et que la valeur maximale de ZT peut être efficacement améliorée avec le augmentation de la tension. Sans contrainte, la monocouche d'InSe a une valeur de pic ZT de 0,36 à température ambiante, qui est proche de celle du silicène (0,36), du germanène (0,41) et du MoS monocouche₂ (0,58) [53, 54], et inférieur à celui des monochalcogénures 2D (1,29~2,63 à 700 K) [55]. Compte tenu de la mobilité élevée des porteurs et de la flexibilité mécanique supérieure, la monocouche d'InSe contraint est également un matériau potentiel prometteur pour les applications thermoélectriques. Lorsqu'une contrainte de traction est appliquée, la liaison interatomique affaiblie induit une anharmonicité plus forte. L'augmentation du taux de diffusion des phonons, la diminution de la vitesse des groupes de phonons et la capacité thermique des phonons ont entraîné une réduction de la conductivité thermique du réseau, conduisant à une meilleure figure de mérite. Des calculs théoriques antérieurs ont démontré que la monocouche d'InSe peut supporter une déformation en traction supérieure à 20 %, ce qui est beaucoup plus important que nos déformations prédites [20]. Dans l'expérience, l'application d'une contrainte sur les matériaux 2D se fait principalement par leur interaction avec les substrats, qui peut être induite par le chauffage [56], le décalage de réseau entre les films minces épitaxiaux [57] ou la flexion du matériau 2D sur le substrat [58, 59]. En fait, il est expérimentalement plus courant d'appliquer une déformation uniaxiale au lieu d'une déformation biaxiale. Sur la base des rapports précédents [20], une déformation uniaxiale peut présenter une amélioration similaire sur les propriétés thermoélectriques de la monocouche InSe.

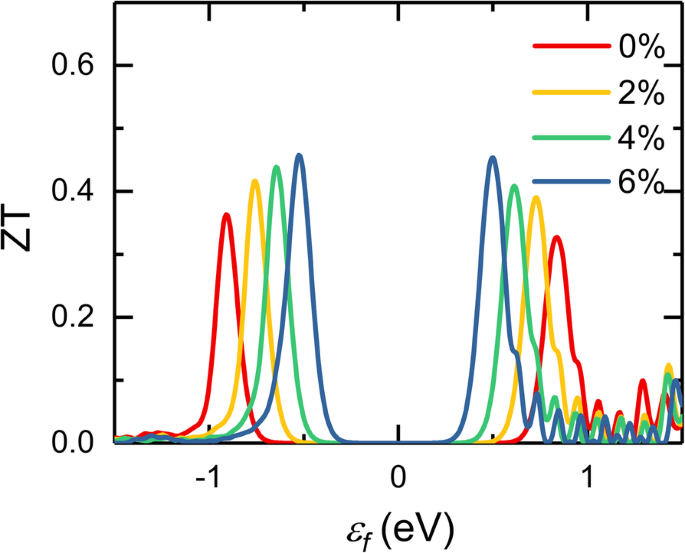
Facteur de mérite calculé de l'InSe monocouche en fonction du potentiel chimique sous différentes contraintes

Conclusion

En conclusion, nous étudions systématiquement l'impact possible de la contrainte de traction biaxiale sur les propriétés de transport électronique, thermoélectrique et de phonons pour la monocouche d'InSe par des calculs de premiers principes. La bande interdite diminue à mesure que l'augmentation de la contrainte de traction, conduisant à la réduction du coefficient Seebeck. La contrainte de traction a également induit une diffusion anharmonique plus forte, et la réduction de la conductivité thermique du réseau pourrait être attribuée à l'augmentation résultante du taux de diffusion des phonons, à la diminution de la vitesse des groupes de phonons et à la capacité thermique des phonons. La réduction de la conductivité thermique du réseau l'emporte sur celle du coefficient Seebeck, entraînant ainsi une performance améliorée avec l'augmentation de la contrainte de traction.

Disponibilité des données et des matériaux

Les jeux de données générés et/ou analysés au cours de la présente étude sont disponibles auprès de l'auteur correspondant sur demande.

Abréviations

2D :

Deux dimensions

CBM :

Bande de conduction minimum

τ :

Moment de détente

C _ph :

Capacité calorifique du phonon

FET :

Transistor à effet de champ

LA :

Dispersion acoustique longitudinale des phonons

PF :

Facteur de puissance

S :

Coefficient de Seebeck

AT :

Dispersion acoustique transversale des phonons

VBM :

Bande de valence maximum

ZA :

z -axe de dispersion acoustique des phonons

ZT :

Figure de mérite

ε _f :

Niveau de Fermi

Κ _e :

La conductivité thermique avec les apports des porteurs électroniques

Κ _l :

La conductivité thermique avec les contributions du réseau

σ :

Conductivité électrique