Bistabilité optique contrôlable et mélange à quatre ondes dans une optomécanique à molécule photonique

Contexte

Les systèmes optomécaniques (OMS) [1], constitués de cavités optiques couplées à des résonateurs mécaniques et explorant les interactions photon-phonon cohérentes induites par la pression de rayonnement, ont récemment attiré beaucoup d'attention car ils offrent une plate-forme pour manipuler les résonateurs mécaniques et les champs électromagnétiques, et ouvrent la voie aux voie pour des applications potentielles de dispositifs optomécaniques, tels que le laser à phonons [2, 3], la détection [4], la compression de phonons [5], la réalisation de la lumière comprimée [6–8], le refroidissement à l'état fondamental [9–11], et la transparence induite par optomécanique (OMIT) [12–15] induite par la lumière stockée dans des dispositifs à semi-conducteurs [16, 17]. Bien que la plus grande attention ait été accordée à l'OMS unique, réaliser des OMS composés en intégrant plus de modes optiques ou mécaniques tels qu'un mode mécanique couplé à deux modes optiques via la pression de rayonnement [18, 19] et l'interaction phononique entre deux résonateurs mécaniques [20 , 21] deviennent une tendance pour approfondir l'étude de l'OMS et de ses applications potentielles dans le traitement de l'information quantique. Sur la base du composé hybride OMS, le transfert d'un état quantique [22], le refroidissement par phonons de type OMIT [23], le mode sombre optomécanique [24] et l'absorption électromagnétique induite par les phonons [25] ont fait l'objet de nombreuses recherches. Dans les nombreux OMS composés, en tant qu'extension naturelle de l'OMS générique, deux microcavités en mode galerie de chuchotement (WGM) directement couplées appelées molécule photonique [26, 27] avec un effet optomécanique dans une microcavité WGM ont attiré beaucoup d'attention. Il existe deux types d'interaction dans le système optomécanique composé de molécules photoniques :le premier est l'interaction optomécanique induite par la pression de rayonnement et l'autre est le couplage cavité-cavité via un effet tunnel de photons accordable. Les deux interactions ensemble donnent lieu à plusieurs phénomènes intéressants, notamment le laser à phonons [2, 3], le chaos [28], le refroidissement de l'état fondamental [23] et le contrôle cohérent de la transmission lumineuse [25, 29, 30].

D'autre part, OMS fournit également une plate-forme pour étudier l'effet non linéaire de l'interaction lumière-matière. Parmi tous les phénomènes non linéaires de l'OMS, la bistabilité optique et le mélange à quatre ondes (FWM) sont des phénomènes optiques non linéaires typiques qui intéressent les chercheurs. Ces dernières années, le comportement bistable du nombre moyen de photons intracavités a été largement étudié dans divers OMS, tels que le système optomécanique à cavité de condensat de Bose-Einstein [31, 32], l'OMS avec un puits quantique [33], les atomes ultrafroids [34, 35], et d'autres OMS hybrides [36, 37]. De plus, FWM peut être décrit comme la cavité entraînée par un puissant laser à pompe avec une fréquence ω _p et une fréquence laser de sonde faible ω _s , puis, deux photons de pompe se mélangeraient à un photon de sonde via le mode mécanique pour produire un photon libre à la fréquence 2ω _p −ω _s dans l'OMS, et il est également étudié dans des travaux antérieurs, tels que la division de mode dans un système optomécanique à couplage fort [38], la conduite mécanique cohérente OMS [39, 40] et un système optomécanique à cavité à deux modes [41]. Cependant, la bistabilité optique et le FWM ont rarement été étudiés dans les OMS composites à molécules photoniques, où la force de couplage représentée par J des deux cavités jouent un rôle clé affectant ces phénomènes optiques non linéaires.

Dans le présent travail, nous considérons un système optomécanique de cavité composite photonique-molécule, composé de deux microcavités WGM, où une cavité WGM est une cavité optomécanique avec une dissipation de cavité élevée κ , et l'autre cavité WGM est une cavité optique ordinaire auxiliaire avec un facteur de qualité (Q) élevé [42]. Comme Liu et al. [43] l'ont démontré, il reste difficile d'atteindre simultanément un facteur Q élevé et un petit volume de mode (V) pour le même type de résonateur. Dans l'optomécanique photonique-molécule, en couplant la cavité optomécanique à l'origine c avec dissipation à haute cavité κ (sans Q élevé) à un mode de cavité auxiliaire a avec un Q élevé mais un V grand, l'exigence d'un Q élevé et d'un V petit pour la même cavité peut être supprimée. Nous introduisons un paramètre de rapport δ =κ _c /κ _un , où κ _c =ω _c /Q _c et κ _un =ω _un /Q _un sont les taux de décroissance des modes de cavité c et un (ω _c et ω _un sont les fréquences de la cavité c et un ) pour étudier l'effet non linéaire dans l'optomécanique des molécules photoniques. Ici, la cavité optomécanique c est entraînée par le laser de pompe tandis que la cavité auxiliaire a est entraîné par le laser de la sonde. La cavité c est couplé à la cavité a par champ évanescent, et la force de couplage J entre les deux cavités peut être contrôlé en faisant varier la séparation entre les deux cavités WGM [26]. Nous étudions la bistabilité optique et le FWM sur la base de la molécule photonique composite OMS en faisant varier la force de couplage J entre les résonateurs à cavité, et une bistabilité optique réglable et contrôlable et un FWM peuvent être obtenus en manipulant la force de couplage J entre les deux cavités. De plus, en ajustant le paramètre δ et la puissance de la pompe P , le processus FWM peut être contrôlé.

Modèle et théorie

L'optomécanique des molécules photoniques est illustrée à la Fig. 1. La première cavité prend en charge un mode optique c avec la fréquence ω _c entraîné par le laser de pompe avec une fréquence ω _p et l'amplitude \(\varepsilon _{p}=\sqrt {P/\hbar \omega _{p}}\). La pression de radiation induit un mode mécanique b avec la fréquence du résonateur mécanique ω _m , et le taux de couplage optomécanique à photon unique est g =g ₀ x ₀ (g ₀ =ω _c /R et R est le rayon de la cavité c ), et la fluctuation du point zéro de la position de l'oscillateur mécanique est \(x_{0}=\sqrt {\hbar /2M\omega _{m}} \) [13]. Ensuite, l'hamiltonien de l'optomécanique c est [13]

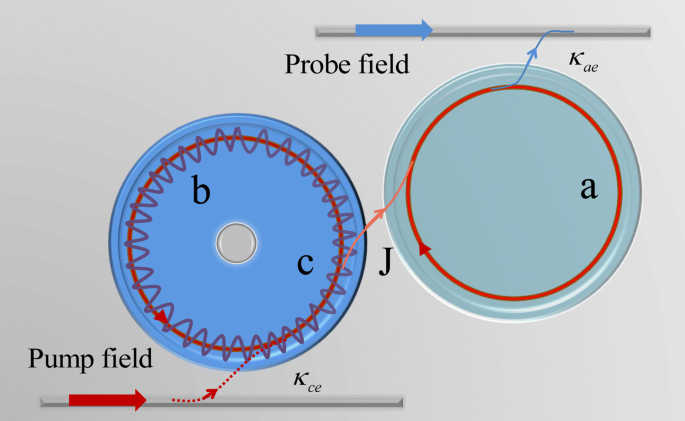
Schéma de principe du système optomécanique de cavité composite photonique-molécule comprenant deux cavités WGM. La première cavité WGM à dissipation élevée κ est la cavité optomécanique c entraîné par un laser de pompe, et la force de pression de rayonnement induit le mode mécanique b couplage à la cavité c avec force de couplage g . La deuxième cavité WGM a est une cavité auxiliaire pilotée par une sonde laser avec un facteur de qualité (Q) élevé. La cavité optomécanique c est couplé à la cavité a via champ évanescent, et on introduit un paramètre J pour décrire la force de couplage des deux cavités, qui peut être contrôlée en faisant varier la séparation entre elles [26]

où Δ _c =ω _c −ω _p est le désaccord du champ de pompage et de la cavité c . c et c ^† représentent les opérateurs d'annihilation et de création bosonique du mode cavité c , et b ^† (b ) est l'opérateur de création (d'annihilation) du mode mécanique. La cavité auxiliaire ne prend en charge qu'un mode optique a entraîné par le laser de la sonde avec la fréquence ω _s , et son amplitude ε _s est \(\varepsilon _{s}=\sqrt { P_{s}/\hbar \omega _{s}}\). Nous introduisons les opérateurs d'annihilation et de création a et un ^† pour décrire la cavité a , et son hamiltonien est [13]

où Δ _un =ω _un −ω _p est le désaccord du champ de pompe et de la cavité a , et Ω =ω _s −ω _p est le désaccord pompe-sonde. Nous utilisons deux fibres coniques pour exciter le mode cavité a et le mode cavité c comme guide d'onde optique avec le taux de couplage κ _ae et κ _ce . La cavité optomécanique c couples à la cavité a à travers un champ évanescent, et le taux de couplage cavité-cavité J peuvent être réglés efficacement en modifiant la distance entre eux [26]. Lorsque la force de couplage J est faible entre les deux cavités, alors l'énergie de la cavité c ne peut pas se transférer facilement dans la cavité a . Inversement, si la force de couplage J augmente avec la diminution de la distance entre les deux cavités, alors l'énergie peut facilement s'écouler des deux cavités. L'interaction linéairement couplée entre les deux cavités est décrite par [26] \(\hbar J\left (a^{\dag }c+ac^{\dag }\right)\). Ensuite, l'hamiltonien total dans le référentiel d'ondes tournantes de la fréquence de pompe ω _c peut s'écrire [3, 13, 23]

Le taux de décroissance du mode deux cavités κ =κ _c =κ _un =κ _ex +κ ₀ avec le taux de perte de photons intrinsèque κ ₀ , et κ _ex décrit la vitesse à laquelle l'énergie quitte la cavité optique dans les champs de propagation [13]. Ici, pour simplifier, nous ne considérons que la condition de κ _ex =κ ₀ =κ _ae =κ _ce , et nous considérons ω _c =ω _un .

On utilise l'équation du mouvement de Heisenberg \(i\hbar \partial _{t}O=[O,H]\) (O =un ,c ,X ) et introduisons les opérateurs d'amortissement et de bruit correspondants, et nous obtenons les équations quantiques de Langevin comme suit [44] :

où X =b ^† +b est l'opérateur de position et γ _m est le taux de décroissance du résonateur. un _dans et c _dans décrivant les bruits de Langevin suivent les relations [45]

Le mode du résonateur est influencé par le processus de force stochastique avec la fonction de corrélation suivante [46]

où k _B est la constante de Boltzmann et T indique la température du réservoir.

Lorsque la cavité optomécanique c est entraîné par un puissant laser à pompe, l'opérateur Heisenberg peut être divisé en deux parties, c'est-à-dire la valeur moyenne en régime permanent O ₀ , et petite fluctuation δ O avec une valeur moyenne nulle 〈δ O =0. Les valeurs en régime permanent déterminent les nombres de photons intracavité (n _un =|un _s | ² et n _c =|c _s | ² ) déterminé par

où \(\Delta ^{^{\prime }}=\Delta _{c}-2g^{2}n_{c}/\omega _{m}\). Cette forme d'équations couplées est caractéristique de la bistabilité optique. Dans la section suivante, nous discuterons des paramètres tels que la puissance de la pompe P , la force de couplage cavité-cavité J , et le paramètre de rapport δ qui affectent la bistabilité optique. Ne garder que les termes linéaires des opérateurs de fluctuation et faire l'ansatz [47] 〈δ un 〉=un ₊ e ^{−i Ω t} +un ₋ e ^{i Ω t} , δ c 〉=c ₊ e ^{−i Ω t} +c ₋ e ^{i Ω t} , δ X 〉=X ₊ e ^{−i Ω t} +X ₋ e ^{i Ω t} , on obtient alors

où \(\Lambda _{1}=igc_{s}^{2}\eta ^{\ast }J^{2}\varepsilon _{s}\sqrt { \kappa _{ae}}\), Λ ₂ =(i Δ _{un 2} +κ _un )(i Δ ₂ +κ _c )[(i Δ ₁ −κ _c )(i Δ _{un 1} −κ _un )−J ² ], \(\Lambda _{3}=-g^{2}\eta ^{\ast 2}n_{c}^{2}(i\Delta _{a1}-\kappa _{a})( i\Delta _{a2}+\kappa _{a})\), Δ _{un 1} =Δ _un −Ω , Δ _{un 2} =Δ _un +Ω , \(\Delta _{1}=\Delta ^{^{\prime }}-\Omega +g\eta n_{c}\), \(\Delta _{2}=\Delta ^{^{\ prime }}+\Omega +g\eta ^{\ast }n_{c}\), et \(\eta =2g\omega _{m}/(\omega _{m}^{2}-i\ gamma _{m}\Omega -\Omega ^{2})\). En utilisant la relation entrée-sortie standard [45] \(a_{\text {out}}(t)=a_{\text {in}}(t)-\sqrt {2\kappa _{a}}a(t )\), où a _sortie (t ) est l'opérateur de champ de sortie et obtenez la valeur attendue des champs de sortie :

où un _sortie (t ) est l'opérateur de champ de sortie. L'équation (13) montre que le champ de sortie se compose de trois termes. Le premier terme correspond au champ de sortie au champ moteur d'amplitude ε _p et fréquence ω _p . Le deuxième terme correspond au champ de sonde de fréquence ω _s lié au champ anti-Stokes résultant de l'OMIT, qui a été étudié dans divers systèmes optomécaniques [12–15, 48]. Le dernier correspond au champ de sortie de fréquence 2 ω _p −ω _s lié au champ de charge affichant le FWM. Dans le processus FWM, les deux photons du champ moteur interagissent avec un seul photon du champ sonde chacun avec des fréquences ω _p et ω _s né un nouveau photon de fréquence 2 ω _p −ω _s . L'intensité FWM en termes de champ de sonde peut être définie comme [49]

qui est déterminé par la force de couplage optomécanique g , la puissance de la pompe P , la force de couplage cavité-cavité J , et le taux de décroissance δ des deux cavités.

Résultats numériques et discussions

Dans cette section, nous étudions d'abord le comportement bistable du nombre de photons en régime permanent n _c et n _un des deux cavités selon les Eqs. (10) et (11). Parce qu'il est trop lourd de donner l'expression analytique de la condition de bistabilité, nous allons présenter ici les résultats numériques. Nous choisissons les paramètres similaires à ceux de la Réf. [13, 26] :les paramètres de la cavité c comme [13] :g ₀ =12 GHz/nm, γ _m =41 kHz, ω _m =51,8 MHz, κ _c =5 MHz, m =20 ng, λ =750 nm, et Q =1500, et l'ordre de grandeur de la puissance de la pompe est milliwatt (1 mW =10 ⁻³ W). Pour la cavité a , nous considérons ω _un =ω _c et κ _c =κ _un . La force de couplage J entre les deux modes de cavité joue un rôle clé et peut affecter le comportement bistable et FWM. Il a été rapporté expérimentalement que la force de couplage J dépend de la distance entre la cavité c et cavité a [26] (la force de couplage diminue également de façon exponentielle avec l'augmentation de la distance des deux cavités). Ici, on attend la force de couplage \( J\sim \sqrt {\kappa _{c}\kappa _{a}}\).

Équations (10) et (11) donnant les nombres de photons intracavité de la cavité optomécanique c et cavité ordinaire a sont des équations cubiques couplées, qui présentent un comportement bistable. On considère d'abord la condition de J =0, c'est-à-dire une seule cavité optomécanique c , et la figure 2a trace le nombre moyen de photons intracavité n _c de cavité optomécanique c en fonction du désaccord de la pompe à cavité Δ _c =ω _c −ω _p avec trois puissances de pompe. Lorsque la puissance de la pompe est inférieure à P =0.4 mW (comme P =0,1 mW), la courbe est presque lorentzienne. En augmentant la puissance P à une valeur critique, la cavité optomécanique c présente un comportement bistable, comme le montrent les courbes pour P =0.4 mW à P =0,8 mW, où la courbe de résonance initialement lorentzienne devient asymétrique. Le nombre moyen de photons intracavité n _c a trois racines réelles (Eq. (10)), et les racines les plus grandes et les plus petites sont stables, et celle du milieu est instable, ce qui est représenté dans un ovale sur la Fig. 2a. Cependant, lorsque l'on considère la cavité optique a , c'est-à-dire J ≠0 tel que J =1.0 κ _un , le comportement bistable est rompu à certains égards, comme le montre la figure 2b. C'est parce que lorsque la cavité optomécanique c couplé à la cavité optique a , parties du nombre de photons intracavité n _c de cavité optomécanique c sera couplé dans la cavité optique a , et par conséquent, le nombre de photons intracavité n _c diminuera et entraînera ensuite un comportement bistable détruit. La figure 2c montre le nombre moyen de photons intracavité n _c de cavité optomécanique c en fonction de la force de couplage cavité-cavité J avec trois puissances de pompe. De toute évidence, le nombre moyen de photons intracavité n _c dépend de la puissance de la pompe P , et le nombre de photons intracavité n _c diminue toujours avec l'augmentation de la force de couplage J parce que des parties du nombre de photons sont couplées dans la cavité optique a . De plus, un désaccord plus grand de la pompe à cavité est bénéfique pour observer le comportement optique bistable avec l'augmentation de la puissance de pompe P . La figure 2d représente le nombre moyen de photons intracavité n _c par rapport à la puissance de la pompe P avec cavité a aux bandes latérales rouges (Δ _un =ω _m ) et bandes latérales bleues (Δ _un =−ω _m ), respectivement, et la bistabilité présente le comportement de la boucle d'hystérésis [50]. Cependant, nos résultats sont différents des travaux précédents de système optomécanique bimode sans considérer le couplage cavité-cavité J . Par conséquent, la force de couplage J joue un rôle important dans la bistabilité.

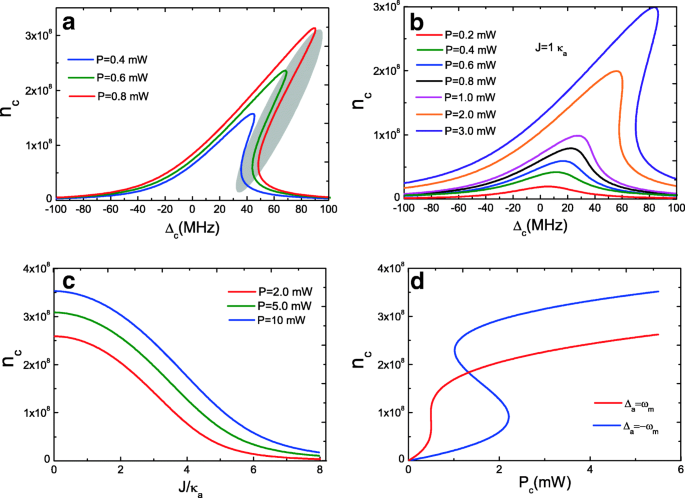
un Nombre moyen de photons intracavité de la cavité optomécanique c en fonction du désaccord de la pompe à cavité Δ _c avec trois puissances de pompe à J =0. b Nombre moyen de photons intracavité de la cavité optomécanique c en fonction du désaccord de la pompe à cavité Δ _c avec plusieurs puissances de pompe différentes sous J =1.0 κ _un . c Nombre moyen de photons intracavité n _c de cavité optomécanique c en fonction de J avec trois puissances de pompe. d Nombre moyen de photons intracavité n _c en fonction de P pour Δ _c =Δ _un =ω _m

Nous étudions en outre le comportement bistable de la cavité optique a avec l'éq. (11). La figure 3a donne le nombre de photons intracavité n _un de cavité ordinaire a en fonction du désaccord de la pompe à cavité Δ _un =ω _un −ω _p avec des puissances de pompage P =0,1 mW, P =1.0 mW, et P =10 mW à J =1.0 κ _un . Il est évident que la cavité optique a ne peut pas se comporter comme un comportement bistable en raison du nombre de photons intracavité n _un de la cavité a de la cavité c ne peut pas maintenir la bistabilité à faible puissance de pompage. En fait, seule la puissance de pompe élevée P peut cavité a présente un comportement bistable, car seule la cavité optomécanique entraînée par une pompe élevée c , beaucoup plus de nombre de photons peuvent se coupler dans la cavité optique a . Nous traçons également le nombre moyen de photons intracavité n _un de la cavité optique a en fonction de la force de couplage J sous trois puissances de pompe comme le montre la figure 3b. Il est clair que lorsque J =0, n _un =0, car il n'y a pas de couplage entre les deux cavités en J =0, et à cette condition, aucun photon ne se couple dans la cavité optique a . Avec l'augmentation de la force de couplage J (en diminuant la distance des deux cavités [26]), les nombres de photons intracavités n _un de cavité optique ordinaire a augmenter mais pas toujours. Il existe une force de couplage optimale J pour la valeur maximale de n _un sous une puissance de pompe différente, puis, n _un diminuera avec l'augmentation de J . C'est un fait remarquable que la force de couplage J entre les deux cavités peut être ajustée [26].

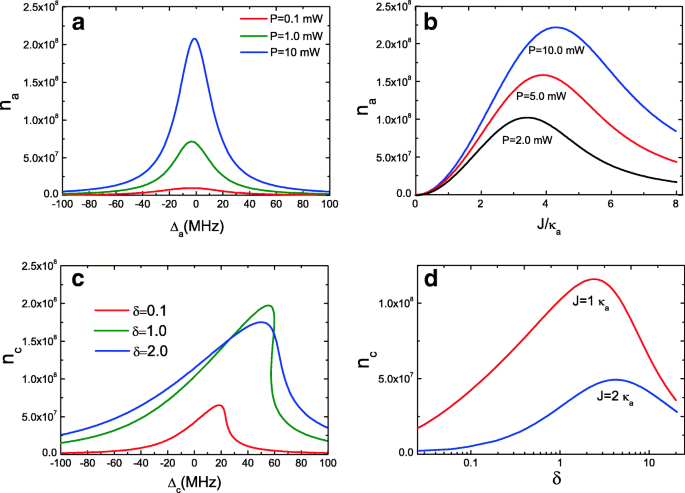
un Nombre moyen de photons intracavitaires de la cavité ordinaire a en fonction du désaccord de la pompe à cavité Δ _un avec trois puissances de pompe à J =1.0 κ _un . b Nombre moyen de photons intracavité n _un en fonction de J avec trois puissances de pompe. c Nombre moyen de photons intracavité n _c en fonction de Δ _c avec trois paramètres de rapport δ . d Nombre moyen de photons intracavité n _c en fonction de δ pour deux J

De plus, nous considérons un paramètre de rapport δ =κ _c /κ _un (κ _c =ω _c /Q _c et κ _un =ω _un /Q _un ) pour étudier les paramètres des deux cavités qui influencent le comportement bistable. κ est le taux de décroissance du mode de la cavité, qui est lié à la fréquence et au facteur de qualité de la cavité. Comme nous le savons, il est difficile d'obtenir un Q élevé et un V faible simultanément pour un mode de cavité en raison de la limite de diffraction. Pour une cavité optique, un V plus petit correspondant à un taux de décroissance radiative plus élevé entraîne un Q inférieur. Bien que différents types de cavités possèdent leurs propres propriétés uniques, le poids entre un Q élevé et un V petit existe toujours. Cependant, lorsqu'en couplant l'OMS à l'origine c avec dissipation à haute cavité vers un mode de cavité auxiliaire a avec un Q élevé mais un V grand, le comportement bistable changera de manière significative. La figure 3c montre le nombre moyen de photons intracavité n _c de cavité optomécanique c en fonction de Δ _un sous plusieurs δ différents =κ _c /κ _un avec une force de couplage J inchangée =1.0 κ _un . Nous pouvons constater que le comportement bistable peut apparaître, mais le nombre de photons intracavité n _c est petit à δ =0.1 avec J =2 κ _un , c'est-à-dire κ _c =0.1 κ _un ce qui signifie Q _c >Q _un . En augmentant le rapport δ de δ =1.0 à δ =2.0, le nombre de photons intracavité n _c subit le changement d'un comportement bistable à un profil de ligne presque lorentzien. C'est-à-dire lorsque Q _c <Q _un , le comportement bistable sera rompu, mais il existe une condition optimale, c'est-à-dire Q _c =Q _un . Sur la Fig. 3d, nous donnons le nombre de photons intracavité n _c en fonction de δ avec deux J différents , et évidemment, en augmentant le paramètre de rapport δ , les nombres de photons intracavité n _c augmenter. Lorsqu'il atteint une valeur optimale pour un J donné , puis n _c diminuer. Par conséquent, contrôler les paramètres de la cavité, comme le taux de décroissance κ ou le facteur de qualité des cavités, le comportement bistable peut être contrôlé.

D'autre part, en tant que phénomène optique non linéaire typique, nous étudions également le processus FWM avec l'équation. (14) dans le système optomécanique de la molécule photonique. La figure 4 trace le spectre FWM en fonction de la cavité sonde a désaccord Δ _s =ω _s −ω _un à Δ _un =Δ _c =0 sous différents régimes de paramètres. La figure 4a–d affiche l'évolution des spectres FWM sous différentes puissances de pompe P à J =1.0 κ _un . Il est clair que les spectres FWM présentent trois pics, où un pic Lorentzien près de Δ _s =0 et deux pics de division de mode se situent à ±ω _m , et l'intensité FWM diminue avec l'augmentation de la puissance de la pompe. La figure 4e–h montre le changement des spectres FWM de J =0,5 κ _un à J =2.0 κ _un à la puissance de la pompe P =1,0 mW. Avec l'augmentation de la force de couplage J de J =0,5 κ _un à J =2.0 κ _un , les spectres FWM changent de manière significative. Les phénomènes peuvent être expliqués avec une image à l'état habillé qui a été démontrée dans un système optomécanique à cavité unique [51].

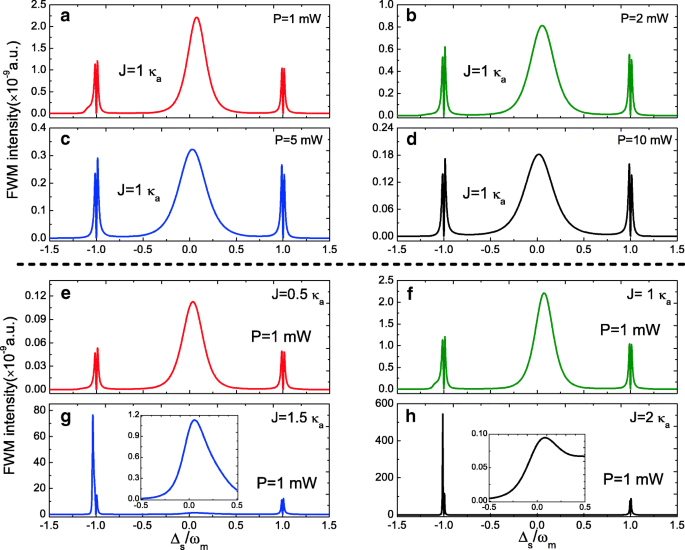
un –d Intensité FWM en fonction du désaccord sonde-pompe normalisé Δ _s pour différentes puissances de pompe à J =1.0 κ _un . e –h Intensité FWM en fonction de Δ _s pour différents J à la puissance de la pompe P =1.0 mW

Nous étudions ensuite les spectres FWM à Δ _un =Δ _c 0. La figure 5a–d donne les spectres FWM au niveau de la bande latérale rouge, c'est-à-dire Δ _un =Δ _c =ω _m sous un J inchangé =1.0 κ _un en augmentant la puissance de la pompe de P =1.0 à P =10 mW. Deux pics de division de mode normaux apparaissent dans les spectres FWM se situant à ±ω _m respectivement, et l'intensité FWM diminue avec l'augmentation de la puissance de la pompe. La figure 5e–h montre les spectres FWM au niveau de la bande latérale rouge, c'est-à-dire Δ _un =Δ _c =ω _m sous une puissance de pompe fixe P =2.0 mW avec augmentation de la force de couplage J de J =0,5 κ _un à J =2.0 κ _un . Évidemment, l'intensité FWM augmente avec l'augmentation de la force de couplage J , et le plus grand J signifie plus de nombres de photons couplés dans la cavité optique a . Lors de la modification du désaccord Δ _un et Δ _c de la bande latérale rouge à la bande latérale bleue, c'est-à-dire Δ _un =Δ _c =−ω _m , l'évolution des spectres FWM change de manière proéminente. La figure 5i–l affiche les spectres FWM sur la bande latérale bleue sous quatre puissances de pompe différentes, et l'intensité FWM diminue avec l'augmentation de la puissance de la pompe même sur la bande latérale bleue. À l'exception de deux pics de division de mode normaux situés à ±ω _m , il y a aussi deux pics de bande latérale nets apparaissent dans les spectres FWM et leur emplacement est lié à la puissance de pompage. Dans la Fig. 5m–p, nous discutons également de la force de couplage J qui affectent les spectres FWM sous la bande latérale bleue. L'apparition d'autres pics de bande latérale dans les spectres FWM dépend de la force de couplage J .

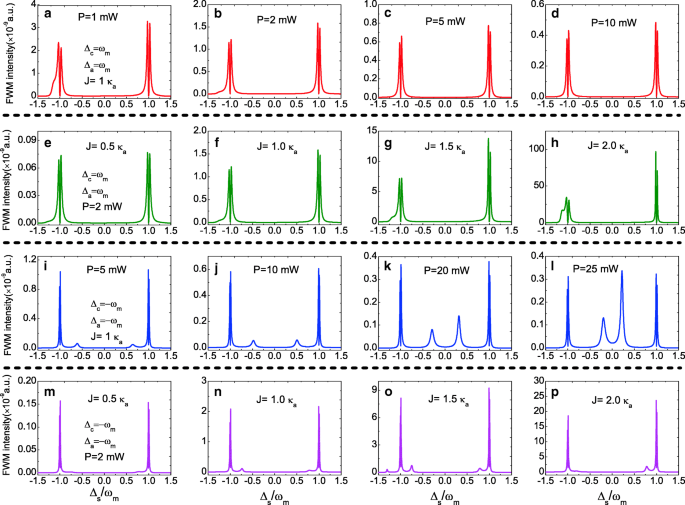
un –d Intensité FWM en fonction de Δ _s pour différentes puissances de pompe P au niveau de la bande latérale rouge (Δ _c =Δ _un =ω _m ) et J =1.0 κ _un . e –h Intensité FWM en fonction de Δ _s pour différents J sous la bande latérale rouge et la puissance de la pompe P =2,0 mW. je –l Intensité FWM en fonction de Δ _s pour différentes puissances de pompe P au niveau de la bande latérale bleue (Δ _c =Δ _un =−ω _m ) et J =1.0 κ _un . m –p Intensité FWM en fonction de Δ _s pour différents J sous la bande latérale bleue et la puissance de la pompe P =2.0 mW

De plus, puisque le paramètre de rapport δ =κ _c /κ _un peut influencer le nombre de photons intracavité dans la molécule photonique composite OMS, les spectres FWM peuvent être manipulés en contrôlant le paramètre δ . La figure 6a–h présente les spectres FWM à paramètres inchangés J =2.0 κ _un et P =10 mW sous la bande latérale rouge en augmentant le rapport δ de δ =0,05 à δ =3.0, et l'intensité FWM diminue avec l'augmentation du rapport δ . Dans la bande latérale bleue, d'autres pics de bande latérale nets apparaîtront dans les spectres FWM, comme indiqué sur la Fig. 6i–p, et l'intensité FWM diminue également avec l'augmentation du rapport δ . Par conséquent, en contrôlant les paramètres de la cavité, comme le taux de décroissance κ ou le Q des cavités, le FWM peut atteindre directement dans la molécule photonique composite OMS.

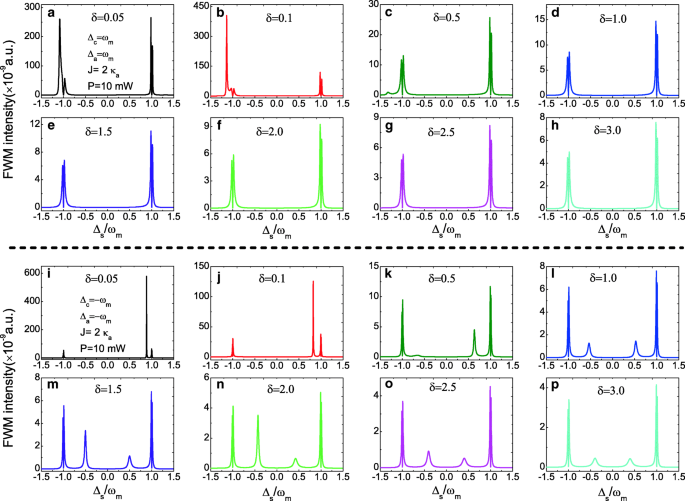
un –h Intensité FWM en fonction de Δ _s pour plusieurs paramètres de rapport différents δ au niveau de la bande latérale rouge (Δ _c =Δ _un =ω _m ) et J =2.0 κ _un , P =10 mW. je –p Intensité FWM en fonction de Δ _s pour plusieurs paramètres de rapport différents δ au niveau de la bande latérale bleue (Δ _c =Δ _un =−ω _m ) et J =2.0 κ _un , P =10 mW

Conclusion

We have investigated the optical bistability and four-wave mixing in a composite WGM cavity photonic-molecule optomechanical system, which includes an optomechanical cavity with high-cavity dissipation coupled to an auxiliary cavity with high-quality factor. We investigate the optical bistability under different parameter regimes such as the coupling strength J between the two cavities and the decay rate ratio δ of the two cavities in the system. The optical bistability can be adjusted by the pump field driving the optomechanical cavity, and the intracavity photon number in the two cavities is determined by the coupling strength J . Further, we have also demonstrated how to control the FWM process in the photonic-molecule optomechanical system under different driving conditions (the red sideband and the blue sideband) and different parameter conditions (the coupling strength J and the ratio δ ). Numerical results show that the FWM process can be controlled with such parameters. These results are beneficial for better understanding the nonlinear phenomena in the composite photonic-molecule optomechanical system.

Abréviations

C-OMS:

Cavity optomechanics systems

FWM:

Four-wave mixing

OMS:

Optomechanics systems

OMIT:

Optomechanically induced transparency

Q :

Quality

V:

Volume

WGM:

Whispering gallery mode