Métasurfaces diélectriques d'ordre élevé pour séparateurs de faisceaux de polarisation à haute efficacité et générateurs de vortex optiques

Contexte

Ces dernières années, le contrôle total des ondes électromagnétiques a été un domaine de recherche émergent. Pour la quête de réalisation d'un tel contrôle, les métamatériaux ont attiré une attention significative pour leurs nouvelles propriétés physiques, qui pourraient être artificiellement conçues comme des désirs en structurant leurs constituants [1]. Jusqu'à présent, les métamatériaux ont été utilisés pour obtenir de nombreuses propriétés optiques excellentes, telles que la réfraction négative, la réfraction nulle et la lumière lente. Cependant, le métamatériau tridimensionnel présente de nombreux inconvénients, tels que des pertes intrinsèques élevées et une difficulté de fabrication, qui limitent ses applications réelles. Avec les développements de la nanotechnologie, des métamatériaux bidimensionnels, ou soi-disant métasurfaces, ont été proposés pour éviter ces inconvénients en raison de leurs structures ultrafines sous-longueur d'onde, de leur fabrication relativement facile et de leurs intégrations conformes aux systèmes [2, 3]. Les métasurfaces consistent généralement en un réseau de résonateurs optiques avec une période inférieure à la longueur d'onde et fonctionnent comme des discontinuités d'interface. Il pourrait introduire un changement brusque dans l'amplitude ou la phase du faisceau incident en concevant la géométrie du résonateur. Sur la base de ce concept, diverses métasurfaces avec différentes fonctions ont été implémentées, notamment un guide d'onde accordable [4, 5], des plaques d'onde [6, 7], une lentille [8,9,10,11], une réfraction anormale [12, 13] , générateurs de vortex compacts [14,15,16] et hologrammes à haute résolution [17,18,19].

Bien que la métasurface présente une efficacité bien meilleure par rapport aux métamatériaux tridimensionnels, la perte doit toujours être considérée sérieusement en raison de l'utilisation courante du métal. Par conséquent, il existe des méthodes améliorées pour augmenter l'efficacité de la transmission, notamment les métasurfaces de Huygens et les métasurfaces entièrement diélectriques. Les métasurfaces de Huygens pourraient éviter une faible efficacité ; néanmoins, la fabrication des structures tridimensionnelles entrave encore ses applications dans la réalité [20]. Heureusement, les métasurfaces diélectriques pourraient être optimisées pour posséder simultanément des résonances électriques et magnétiques qui se chevauchent aux mêmes fréquences et permettre ainsi une pleine 2π contrôle de phase avec une efficacité de transmission élevée [21,22,23,24,25,26,27]. Cependant, la plupart des dispositifs optiques démontrés dans les travaux précédents utilisent le ±1er les modes de diffraction d'ordre pour manipuler le front d'onde de la lumière plutôt que les modes d'ordre élevé [28,29,30]. Récemment, une nouvelle approche a été proposée pour contrôler le front d'onde incident et fonctionne dans des modes d'ordre élevé en modulant la phase discrète; encore, ils ont obtenu des efficacités de transmission assez faibles en raison de la perte ohmique intrinsèque du métal [31, 32].

Dans ce travail, nous proposons une métasurface diélectrique pour manipuler le front d'onde fonctionnant dans des modes de diffraction d'ordre élevé avec une efficacité de transmission extrêmement élevée. Sur la base de la métasurface diélectrique proposée, deux séparateurs de faisceaux polarisants avec des discontinuités de phase abruptes ont été conçus dans la bande des télécommunications et fonctionnant dans des modes d'ordre élevé. Les séparateurs de faisceaux polarisants sont capables de générer deux fronts d'onde différents pour deux polarisations d'entrée orthogonales avec un rendement extrêmement élevé jusqu'à 88 %. En outre, nous avons également conçu deux générateurs de faisceaux vortex avec les charges topologiques de 2 et 3 pour démontrer davantage la capacité de la métasurface conçue à manipuler la lumière dans des modes de diffraction d'ordre élevé.

Méthodes

Le schéma des métasurfaces diélectriques conçues est montré dans l'encart de la figure 1a. Il est composé de nanobriques de silicium cristallin de 900 nm d'épaisseur gravées sur un substrat de verre de 200 nm d'épaisseur, dont les indices de réfraction sont respectivement de 3,48 et 1,48. En raison de son indice de réfraction élevé, le silicium présente des propriétés de résonance de haute qualité et de faibles pertes ohmiques intrinsèques. De plus, le silicium nanostructuré peut être facilement obtenu par une technologie mature de semi-conducteur à faible coût de fabrication, comme EBL et FIB. Le SiO ₂ substrat a été utilisé en raison du fait que la perte de réflexion et la perte d'absorption peuvent être presque négligées dans la longueur d'onde de 1500 nm. La constante de réseau est choisie comme S = 650 nm. Ainsi, la phase géométrique de la lumière transmise induite par une nanotige de silicium dépend des dimensions de la nanobrique le long des directions X et Y. La simulation numérique est réalisée par la méthode FDTD (finite-different time-domain). Dans les simulations, la couche parfaitement adaptée (PML) a été ajoutée à la couche au-dessus et au-dessous d'une cellule pour fonctionner comme des conditions aux limites absorbantes. De plus, les conditions aux limites périodiques (PBC) ont également été appliquées autour d'une maille ou d'une maille élémentaire. La longueur d'onde de fonctionnement est choisie pour être de 1500 nm pour la longueur d'onde des communications optiques.

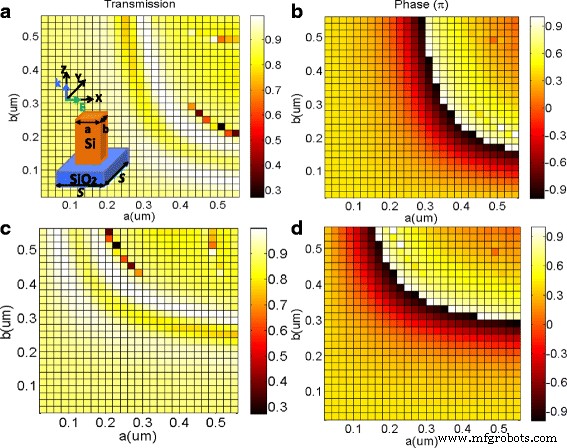
un L'efficacité de la transmission et b les variations de phase correspondantes de la lumière XLP en fonction des paramètres a et b . c L'efficacité de transmission co-polarisée et d variations de phase correspondantes de la lumière YLP en fonction des paramètres a et b . L'encart dans a montre schématiquement la cellule unitaire de la métasurface diélectrique périodique constituée d'un réseau de nanobriques de silicium au-dessus de SiO₂ substrat. L'épaisseur des nanobriques de silicium et SiO₂ le substrat est défini sur 900 nm et 200 nm, respectivement

En utilisant la simulation numérique, comme illustré sur la figure 1, l'efficacité transmise co-polarisée et les variations de phase correspondantes pour la lumière à polarisation linéaire X (XLP) et la lumière à polarisation linéaire Y (YLP) sont calculées en tant que fonctions de les géométries des briques de silicium. Lorsque la lumière XLP est incidente sur la métasurface diélectrique proposée, la transmittance est élevée pour presque toutes les dimensions des nanobriques, comme le montre la figure 1a. Pendant ce temps, la figure 1b implique une gamme complète de phases de 0 à 2π dans la transmission de la lumière XLP, ce qui pourrait fournir une couverture complète de la phase du front d'onde. Plus important encore, pour la grande majorité des dimensions, les nanobriques ont une efficacité de transmission de puissance copolarisée de plus de 88 %, ce qui pourrait être attribué à la faible réflexion et à presque aucune absorption de la métasurface diélectrique à la longueur d'onde des télécommunications. L'efficacité de transmission co-polarisée et les variations de phase correspondantes sous l'incidence YLP sont tracées sur les figures 1c, d, respectivement. En raison de la symétrie, la dépendance des propriétés optiques de la métasurface diélectrique sur les dimensions géométriques de la lumière YLP est similaire à celle de la lumière XLP, ce qui est clairement illustré sur la figure 1. Par conséquent, pour la lumière YLP, l'efficacité de transmission co-polarisée est également supérieur à 88 % et la plage de phase modulante peut varier de 0 à 2π .

Bref, une gamme complète de contrôle de phase de 0 à 2π pourrait être efficacement atteint dans le cas des incidences XLP et YLP en modifiant uniquement la dimension géométrique de la nanobrique le long de la direction X (c'est-à-dire, a ) et la direction Y (c'est-à-dire, b ), respectivement. Par conséquent, la plage de contrôle de phase pourrait être étendue aux modes de diffraction d'ordre élevé (c'est-à-dire de 0 à N × 2π ) en raison de la périodicité de la phase. Pour démontrer la polyvalence et le contrôle de phase précis des nanobriques conçues, deux dispositifs optiques de type transmission à haut rendement ont été proposés en concevant bien la métasurface avec un agencement simple, y compris deux diviseurs de faisceau polarisants et un générateur de vortex optique.

Résultats et discussion

Conception des séparateurs de faisceaux polarisants

Le contrôle de polarisation sur puce est un enjeu important pour les circuits intégrés photoniques. Le séparateur de faisceau polarisant est l'un des dispositifs optiques essentiels utilisés pour contrôler la polarisation sur une puce, qui peut être utilisé pour séparer la lumière d'entrée en deux composantes de polarisation orthogonales [33, 34]. Selon les résultats de la simulation ci-dessus, des séparateurs de faisceau à biréfringence orientable basés sur la métasurface diélectrique proposée pourraient être réalisés, ce qui indique que deux phases différentes de la lumière de réfraction XLP (φ _x ) et lumière de réfraction YLP (φ _y ) pourraient être obtenus simultanément en sélectionnant de manière appropriée les diamètres des nanobriques a et b , respectivement. Ainsi, nous concevons ici des métasurfaces et utilisons cette nouvelle propriété pour réaliser des séparateurs de faisceaux polarisants afin de distinguer deux polarisations orthogonales de la lumière d'entrée dans deux directions avec une efficacité hautement transmise jusqu'à 88 %. De plus, la métasurface conçue pourrait fonctionner non seulement dans les modes de diffraction du premier ordre mais aussi dans les modes de diffraction d'ordre supérieur.

Nous concevons les séparateurs de faisceaux polarisants par 13 nanobriques diélectriques avec trois permutations différentes pour générer différents modes de diffraction d'ordre avec un rendement élevé. Dans la conception de la métasurface 1 (M ₁ ), on discrétise la plage de phase de 0 à 2π et à partir du 2π à 0 en 13 nanobricks avec un pas égal de 2π /13 et -2π /13 pour la lumière transmise polarisée X et Y, respectivement. Les dimensions latérales des 13 nanobriques de silicium sélectionnées sont numérotées par ordre croissant, comme le montre la première ligne de la figure 2a. Apparemment, la plage de contrôle de phase pourrait être étendue au mode de diffraction d'ordre élevé en sélectionnant de manière appropriée les cellules unitaires dans M ₁ et les réorganiser. Par exemple, si nous étendons le mode de diffraction au Nième ordre, la plage de phase devrait couvrir de 0 à N × 2π et de N × 2π à 0 avec une différence de phase de N × 2π /13 et −N × 2π /13 entre deux nanobriques voisines pour la lumière transmise polarisée X et Y, respectivement. Par conséquent, la deuxième ligne de la figure 2a présente les supercellules réarrangées pour le mode de diffraction du troisième ordre (M ₃ ), dont la plage de contrôle de phase est de 0 à 3 × 2π et à partir de 3 × 2π à 0 avec une différence de phase de 3 × 2π /13 et −3 × 2π /13 entre deux nanobriques voisines pour la lumière transmise polarisée X et Y, respectivement. De plus, la métasurface (M ₅ ) pour le mode de diffraction du cinquième ordre est également construit par un ensemble de 13 nanobriques diélectriques, qui sont également réarrangées pour couvrir toute la plage de contrôle de phase de 0 à 5 × 2π et à partir de 5 × 2π à 0 avec une différence de phase de 5 × 2π /13 et −5 × 2π /13 entre deux nanobriques voisines pour la lumière transmise polarisée X et Y, respectivement, comme présenté dans la troisième ligne de la figure 2a. Afin de montrer clairement l'idée, les phases de transmission des 13 antennes dans trois permutations concrètes sous lumière XLP et YLP sont tracées sur la figure 2b.

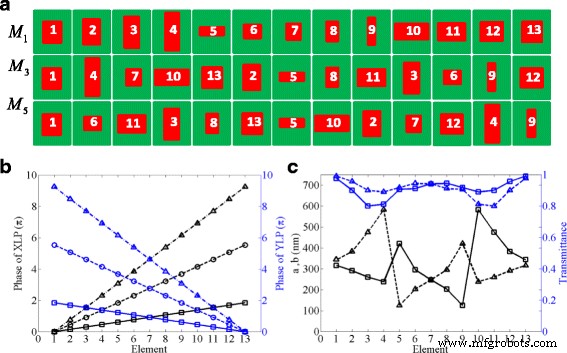
Conception des métasurfaces diélectriques avec trois modes de diffraction d'ordre différent. un Schémas des dimensions latérales des 13 nanobriques conçues. Première ligne M ₁ :une supercellule avec une phase transmise allant de 0 à 2π . Deuxième ligne M ₃ :une supercellule réarrangée avec une phase allant de 0 à 3 × 2π . Troisième ligne M ₅ :une supercellule réarrangée avec une phase allant de 0 à 5 × 2π . b Les phases de transmission simulées des 13 nanobriques conçues de trois modes différents sous XLP (lignes noires ) et YLP (lignes bleues ) incidences, respectivement. c un (lignes pleines noires ) et b (lignes pointillées noires ) des 13 nanobriques utilisées dans les métasurfaces conçues M ₁ . Les lignes bleues représentent les efficacités transmises des 13 nanobricks dans M ₁ sous XLP (traits pleins ) et YLP (lignes pointillées ) incidences, respectivement

De plus, les transmissions des 13 nanobriques conçues sous lumière XLP et YLP ont été simulées et concordent bien avec la prédiction théorique. La figure 2c montre les dimensions géométriques des nanobriques de silicium et les efficacités transmises des 13 nanobricks dans la métasurface M ₁ sous XLP et YLP light. Les transmissions co-polarisées de la plupart des nanobriques diélectriques sont comparables et restent supérieures à 88% bien qu'il y ait des transmissions de deux nanobricks gardant près de 80%. Ces résultats de simulation vérifient que nos métasurfaces conçues pourraient être appliquées pour fabriquer de nombreux dispositifs optiques à haute efficacité.

Des simulations numériques du séparateur de faisceau polarisant sont effectuées en éclairant les métasurfaces conçues M ₁ en incidence normale avec l'angle polarisé de 45 ^° . La lumière concrète XLP et YLP a pu être extraite de l'ensemble des champs transmis, comme représenté sur la figure 3a. Il est clair qu'il existe un front d'onde bien défini et les efficacités transmises co-polarisées de M ₁ sont tracées en fonction de l'angle transmis sur la figure 3b. Les angles transmis co-polarisés de crête sont de -10,2 ^° et 10.2 ^° pour les lumières XLP et YLP transmises, respectivement. Les rendements du premier ordre sont T _xx = 85,9% et T _aa = 88,4% pour les lumières XLP et YLP transmises, respectivement, où T _xx est le coefficient de transmission simulé de la lumière XLP avec l'incidence XLP et T _aa est le coefficient de transmission simulé de la lumière YLP avec l'incidence YLP. Par rapport à l'efficacité transmise des réseaux de nanobriques spatialement homogènes, l'efficacité de conversion est légèrement réduite en raison du couplage entre des résonateurs de dimensions différentes [35]. Sur la base de la loi de Snell généralisée, l'angle de diffraction de la lumière incidente sur une métasurface à gradient peut être calculé par θ _t = sin ⁻¹ [(λ ₀ /n _t L ) + n _i péché(θ _i )/n _t ], où n _t et n _i sont les indices de réfraction du support dans les côtés transmission et incident de l'interface, respectivement, θ _i est l'angle incident, λ ₀ est la longueur d'onde de la lumière dans le vide, et L est la longueur d'une supercellule [36]. Ainsi, les résultats théoriques des angles de diffraction du premier ordre sont de ±10,22 ^° . La simulation numérique et la théorie s'accordent bien. C'est-à-dire que le dispositif conçu peut servir de séparateur de faisceau polarisant avec un traitement successif approprié. De plus, le front d'onde incident n'a pratiquement pas été affecté par la lumière réfléchie de la métasurface, ce qui vérifie que toute la lumière incidente a pu être transmise à partir des métasurfaces avec une efficacité extrêmement élevée.

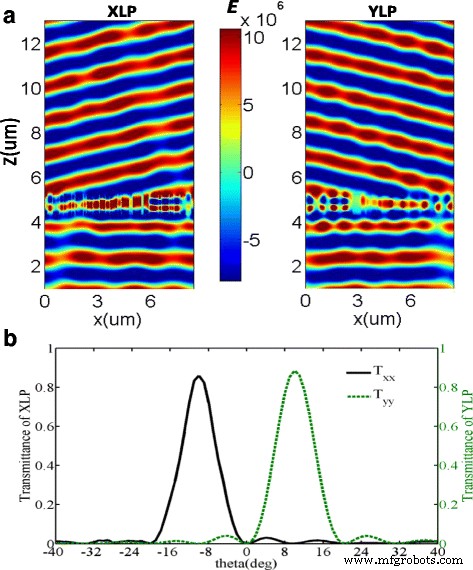
un Les distributions de champ électrique (E ) du XLP transmis extrait (gauche ) et YLP (à droite ) lumière, quand une lumière incidente normale avec 45 ^° polarisation linéaire à la longueur d'onde de 1500 nm transmise à travers les métasurfaces conçues. b Les efficacités transmises co-polarisées des métasurfaces conçues en fonction de l'angle transmis sous les éclairages d'une lumière polarisée X et Y, respectivement

À titre de comparaison, la figure 4 montre les distributions concrètes de champ électrique transmis XLP et YLP des deux autres métasurfaces diélectriques réarrangées constituées de nouvelles supercellules conçues (M ₃ et M ₅ ) sous le 45 ^° lumière incidente à polarisation linéaire. Étant donné que la plage de phase transmise des deux supercellules a été modifiée, les angles de diffraction de M ₃ et M ₅ sont théoriquement calculés à ±32,18 ^° et ±62,56 ^° , respectivement. Sur la figure 4a, b, il existe deux fronts de phase bien définis avec des angles de diffraction du troisième ordre de −32 ^° et 32 ^° pour les lumières XLP et YLP transmises, respectivement. Sur la figure 4c, d, l'angle de diffraction du cinquième ordre est de −63 ^° et 63 ^° pour les lumières XLP et YLP transmises, respectivement. De plus, les efficacités transmises co-polarisées simulées des métasurfaces conçues composées de supercellules réarrangées M ₃ et M ₅ ont également été illustrés sur les figures 5a, b, respectivement. Les angles de transmission de crête correspondent bien aux angles de diffraction théoriques calculés par la loi de Snell généralisée, et les efficacités de diffraction co-polarisée du troisième ordre sont de 82 et 84% pour les lumières XLP et YLP transmises. Cependant, les efficacités de diffraction copolarisée du cinquième ordre ne sont que de 73,5 et 78,4% pour les lumières XLP et YLP transmises, ce qui est essentiellement causé par le couplage EM indésirable entre des nanobriques voisines de géométries différentes. Par conséquent, les métasurfaces conçues pourraient bien fonctionner dans des modes de diffraction d'ordre supérieur en modifiant simplement la disposition des 13 nanobriques diélectriques. Plus important encore, il est démontré que le mode de diffraction peut être personnalisé en contrôlant la différence de phase entre les nanobriques diélectriques adjacentes dans une supercellule.

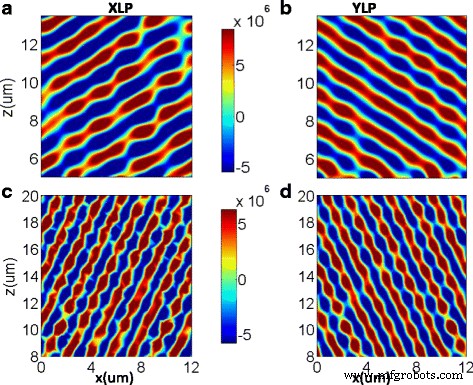
Les distributions de champ électrique du XLP transmis extrait (gauche ) et YLP (à droite ) sous l'incidence normale de 45 ^° lumière à polarisation linéaire vers les métasurfaces de M ₃ (un , b ) et M ₅ (c , d ), respectivement

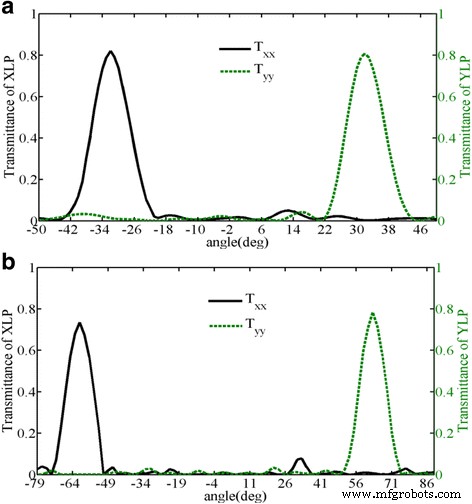
Les efficacités transmises co-polarisées des métasurfaces conçues composées de supercellules réarrangées a M ₃ et b M ₅ en fonction de l'angle transmis sous l'éclairage d'une lumière polarisée X et Y, respectivement

Conception des générateurs optiques de vortex

Le faisceau de vortex optique a un front d'onde hélicoïdal et porte un moment angulaire orbital de lℏ [37, 38], ce qui en fait de grandes promesses en lithographie haute résolution [39, 40], en piégeage optique [41, 42], en communication optique [43, 44], etc. Ici, la charge topologique l est le nombre de torsions du front d'onde et ℏ est la constante de Planck réduite. Le faisceau vortex avec la charge topologique de 1 peut être généré par des métasurfaces avec un profil de phase en spirale allant de 0 à 2π avec un incrément de phase identique le long de la direction azimutale. Par conséquent, pour démontrer davantage la capacité de la métasurface conçue à manipuler la phase transmise et le mode de diffraction, nous concevons un générateur de vortex qui peut convertir un faisceau gaussien homogène incident en un faisceau de vortex. Pour atteindre cet objectif, nous organisons les 13 nanobriques diélectriques de M ₁ dans les 13 secteurs pour introduire un incrément de phase de gradient de 2π /13dans la direction azimutale. Les profils d'intensité transmis sous incidence XLP à z = 10 μm sont représentés sur la figure 6a et ont le minimum d'intensité caractéristique au centre correspondant à une singularité de phase. Les modèles de phase spatiale avec un saut de phase abrupt évident de −π à π dans un délai de 2π la plage azimutale est indiquée sur la figure 6d, ce qui indique que la charge topologique des dispositifs optiques sur la figure 6d est de 1.

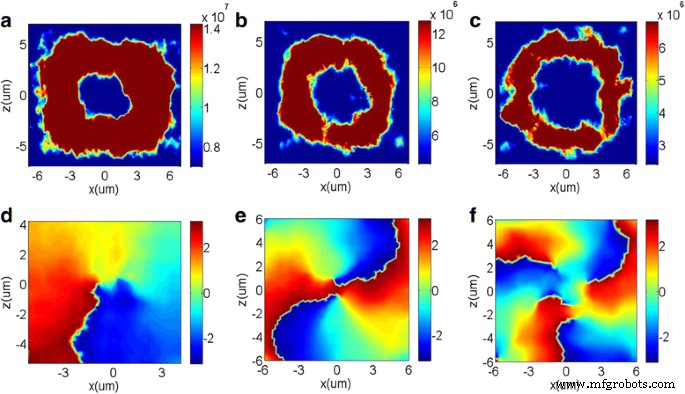
un –c Les distributions d'intensité transmise et d –f les fronts d'onde de phase des faisceaux tourbillonnaires générés à z = 10μm avec une charge topologique de l = 1 , 2 , 3 basé sur les métasurfaces M ₁ , M ₂ , et M ₃ sous l'incidence polarisée X, respectivement

De plus, nous concevons deux autres générateurs de vortex pour générer des faisceaux de vortex en modifiant la disposition des nanobriques dans M ₁ . Ces deux générateurs de faisceaux vortex possèdent les charges topologiques de 2 et 3, respectivement. Leurs profils d'intensité transmise sous l'incidence du XLP sont illustrés respectivement aux Fig. 6b, c. Les approches de conception concrètes modulent la différence de phase des nanobriques à 4π /13 et 6π /13entre deux nanobriques diélectriques voisines, qui sont définies comme M ₂ et M ₃ . Par conséquent, les profils de phase spatiale instantanée de la Fig. 6e, f possèdent deux et trois sauts de phase abrupts évidents de −π à π , respectivement. Le passage de la polarisation incidente de XLP à YLP ne modifie pas le schéma d'intensité de sortie, mais la direction de torsion du front d'onde hélicoïdale sera inversée en raison de la diminution de la différence de phase entre les nanobriques voisines. En outre, il convient de noter que les profils de phase d'ordre supérieur pourraient également être générés par nos métasurfaces diélectriques conçues.

Conclusions

En conclusion, nous avons démontré que les métasurfaces à gradient diélectrique consistent en un arrangement périodique de nanobriques de silicium de tailles différentes, qui pourraient transmettre la lumière d'entrée avec une gamme complète de phases de manipulation de 0 à 2π et un rendement extrêmement élevé (plus de 88 %) à la longueur d'onde des télécommunications. Sur la base des métasurfaces diélectriques conçues, de nouveaux séparateurs de faisceaux polarisants fonctionnant dans les modes de diffraction d'ordre supérieur sont proposés pour séparer deux lumières polarisées d'entrée orthogonales dans des directions différentes arbitraires. De plus, nous avons également conçu deux générateurs de faisceaux vortex fonctionnant dans les modes de diffraction d'ordre supérieur avec des charges topologiques différentes. Notre travail pourrait également être facilement étendu à la conception d'autres dispositifs de transmission optique à haut rendement.