Couplage fort entre une molécule quasi-unique et une cavité plasmonique dans le système de piégeage

Introduction

Ces dernières années, l'utilisation de pièges dipolaires optiques pour piéger et refroidir des atomes ou des molécules a été une technologie prometteuse pour atteindre le condensat de Bose-Einstein, tester les lois physiques fondamentales et mesurer plus précisément les constantes physiques de base [1–3]. Les pièges optiques dipolaires utilisent principalement les forces de gradient de la lumière incidente pour produire un effet dipolaire sur un atome. Pour les pièges à désaccord rouge, les atomes sont piégés dans la position où l'intensité lumineuse est la plus forte sous potentiel attractif [4]. En raison de la diffusion Rayleigh et Raman, les atomes piégés seront soumis à une cohérence atomique apparente et à un effet de chauffage. Dans le même temps, dans la position de lumière la plus forte, le niveau d'énergie nucléaire a un grave décalage de fréquence optique [1]. Au contraire, pour les pièges à désaccord bleu [5, 6], les atomes sont piégés dans la zone d'intensité lumineuse la plus faible sous potentiel d'exclusion [6-8]. Par rapport aux pièges à désaccord rouge, le taux de diffusion d'un photon peut être considérablement réduit avec une faible intensité de lumière incidente, ce qui fournit un moyen plus stable de piéger les petites particules. Cependant, la construction des pièges à désaccord bleu est souvent complexe [9, 10]. Les polaritons de plasmons de surface (SPP) sont des modes hybrides d'ondes lumineuses couplées à des oscillations d'électrons libres confinées à l'interface entre un diélectrique et un métal, qui ont un potentiel énorme pour un large éventail d'applications dans le domaine des dispositifs THz [11-14], matériaux [15], capteurs [16], méta-surface [17] et traitement de l'information quantique [18]. La combinaison du piégeage optique et des structures plasmoniques est une possibilité pour développer des composants optiques intégrés. Par exemple, Chang et al. proposé d'utiliser une nanostructure avec une cavité combinée de nanopointe et de microdisque pour le piégeage d'atomes isolés [19] ; Chen et al. ont obtenu un piégeage d'atomes 3D stable basé sur une lumière désaccordée en bleu dans un réseau de nanotrous plasmoniques [20]. Une nanostructure plasmonique périodique avec un réseau de trous de sous-longueur d'onde possède une propriété optique intéressante, ce qui est un scénario encourageant pour piéger une petite particule telle qu'un atome ou une molécule.

Un couplage fort entre une cavité plasmonique et une molécule n'attire pas seulement l'intérêt pour l'étude fondamentale du phénomène électrodynamique quantique, mais a également de belles perspectives dans le traitement de l'information quantique [21-23]. Les cavités plasmoniques, qui peuvent améliorer considérablement la force de l'interaction lumière-matière, sont un candidat approprié pour réaliser le couplage fort à température ambiante [24–26]. Cependant, le couplage d'une seule molécule avec une cavité plasmonique est un énorme défi à la fois en théorie et en expérience, qui est difficile à manipuler la position de la molécule dans le système de couplage.

Dans cet article, nous étudions théoriquement le couplage fort entre une molécule quasi-simple et une cavité plasmonique pour chaque unité d'un système de piégeage bleu désaccordé. Le système de piégeage à désaccord bleu est composé d'un réseau de nanotrous en or, et chaque unité ne piège qu'une molécule. La méthode du domaine temporel aux différences finies (FDTD) est utilisée pour simuler notre structure, et le spectre de transmission peut être obtenu. Lorsque la molécule est piégée au point le plus faible, le spectre de diffusion présente un dédoublement de Rabi, signature d'un régime de couplage fort. La structure proposée fournit un moyen potentiel pour réaliser le couplage fort entre une molécule quasi-unique et une cavité plasmonique dans le système de piégeage optique.

Méthodes

Nous concevons une structure de nanotrous périodiques pour obtenir le piégeage désaccordé bleu. Nos simulations sont basées sur des méthodes FDTD, et nous adoptons le logiciel EAST FDTD pour définir notre structure et étudier le spectre de transmission et la distribution électromagnétique. Dans notre modèle, une série d'unités de nanotrous d'or avec un rayon R sont disposées dans un film Au bidimensionnel (2D) dans le X -Oui plan et l'épaisseur du film d'Au est de 400 nm. La constante de réseau L et le rayon R sont respectivement de 1000 nm et 250 nm. Lors de notre simulation, l'indice de fond est de 1 et le réseau est de 5 nm pour chaque direction. Les conditions aux limites périodiques sont définies le long du X -axe et Y -axe. La couche de correspondance parfaite est définie le long du Z -axe. Le nombre de la couche d'appariement parfait est de 32. La constante diélectrique de Au est obtenue de Johnson et Christy [27]. La lumière à polarisation circulaire est normalement injectée sur la surface de la structure proposée le long du Z -axe, et la longueur d'onde est de 696 nm. Un X -Oui l'enregistreur plan est à 400 nm de la surface de la structure proposée pour calculer la transmission et un X -Z L'enregistreur plan est au centre de la structure pour obtenir la distribution du champ électromagnétique. En raison de la propriété de la source dipolaire dans la simulation FDTD [28-30], nous pouvons utiliser la source dipolaire pour simuler la molécule. La longueur d'onde de résonance de la molécule est de 707 nm et le taux de décroissance est de 1,1 × 10 ¹⁴ Hz. Dans notre simulation, la transmission T est calculé en intégrant le vecteur de Poynting sur l'extrados et en le normalisant à celui obtenu en l'absence de la structure métallique [31]. La transmission calculée dans la simulation FDTD est notée T =Je _T /(Je _C +Je _D ), où I _T est l'intensité du champ électromagnétique de la transmission, I _C est l'intensité du champ électromagnétique de la lumière à polarisation circulaire, et I _D est l'intensité du champ électromagnétique du dipôle.

Résultats et discussion

Structure de piégeage

La nanostructure plasmonique avec un réseau de trous de sous-longueur d'onde présente un effet de transmission optique extraordinaire qui augmentera considérablement le champ électrique local à proximité des nanotrous [32-34]. Nous utilisons cet effet sur les mouvements moléculaires. Lorsqu'un champ de résonance plasmonique est désaccordé en bleu à partir de la résonance moléculaire, une force répulsive géante de la molécule peut être produite et un minimum de piégeage à environ des centaines de nanomètres de la surface de la structure sera créé. Nous concevons une nanostructure plasmonique périodique pour démontrer notre approche, comme le montre la figure 1.

Schéma de principe de la nanostructure plasmonique périodique

Dans cette section, nous discutons uniquement des résultats de la simulation sans molécule. Nous utilisons une lumière à polarisation circulaire pour éclairer normalement la structure à partir du Z direction à l'infini, et le spectre de transmission est affiché sur la figure 2.

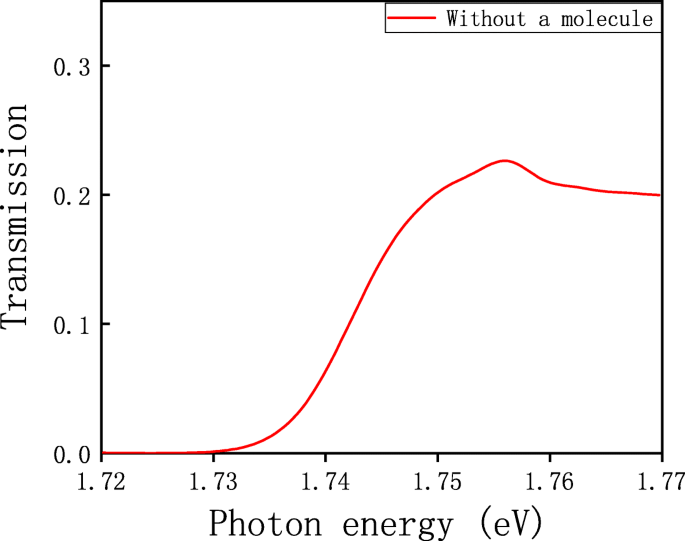
Le spectre de transmission de la structure sans molécule

Un pic de résonance est observé à 707 nm (1,756 eV), qui provient de l'interaction entre les unités (les trous). Ce pic est proche de la longueur d'onde d'ordre (1, 1) de l'anomalie de Wood [35]. Un réseau de trous de sous-longueur d'onde a une diffusion de Bragg vers les SPP, provoquant un vecteur de réseau réciproque du réseau qui peut facilement satisfaire la condition d'accord de phase [20]. Ainsi, la lumière incidente peut exciter les SPP, et cette façon d'exciter les SPP est beaucoup plus facile que d'utiliser la structure de Kretschmann et n'est pas influencée par l'épaisseur du métal. Dans le but d'étudier la distribution spatiale du champ électromagnétique du système, nous traçons une figure de |E | ² distribution du X -Z avion à Y =0 à la longueur d'onde de résonance de 707 nm, illustrée à la Fig. 3a.

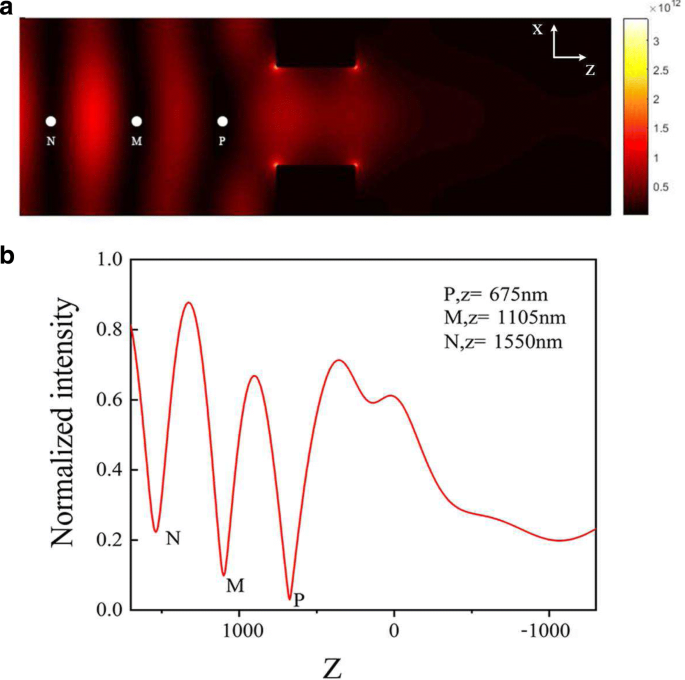
un Intensité du champ électromagnétique |E | ² distribution dans le X -Z avion à Y =0 à λ =696 nm. b Distributions d'intensité normalisées de |E | ² contre Z avec X =0 et O =0 dans le X -Z avion

Dans la Fig. 3a, il y a trois minima de |E | ² noté par les points blancs P, M et N; l'apparition de ces trois minima peut être attribuée aux points chauds résultant de la diffusion en champ proche de la lumière par un réseau de nanotrous plasmoniques. En fait, la distribution du champ électromagnétique est la superposition du champ plasmonique de surface et du champ électromagnétique spatial à travers les nanotrous. La courbe de |E | ² contre Z à X =0 et O =0 dans le X -Z plan est également tracé sur la Fig. 3b. Selon le résultat de la simulation de la distribution électromagnétique spatiale, il y aura trois minima d'intensité, ce qui implique le piège optique à désaccord bleu.

Une molécule peut être piégée dans des minima d'intensité de champ électromagnétique via des forces dipolaires optiques avec une lumière désaccordée en bleu. Dans notre simulation, la molécule est traitée comme un système à deux niveaux et peut être simulée comme un dipôle dans la simulation FDTD [28-30]. Le potentiel de piégeage U _option car une molécule est un potentiel dipolaire optique répulsif associé au champ électromagnétique E , qui est donné par [1, 4] :

Ici, α est une polarisabilité réduite, dans notre cas α =−7.87×10 ⁻³⁸ F ·m ² [20]. Par conséquent, sur la base des distributions d'intensité de champ électromagnétique, nous pouvons obtenir les potentiels de piégeage. En utilisant l'éq. (1) et |E | ² distributions de la figure 3a, nous avons calculé le potentiel de piégeage le long de la ligne avec à la fois X =0 et O =0 comme indiqué sur la Fig. 4.

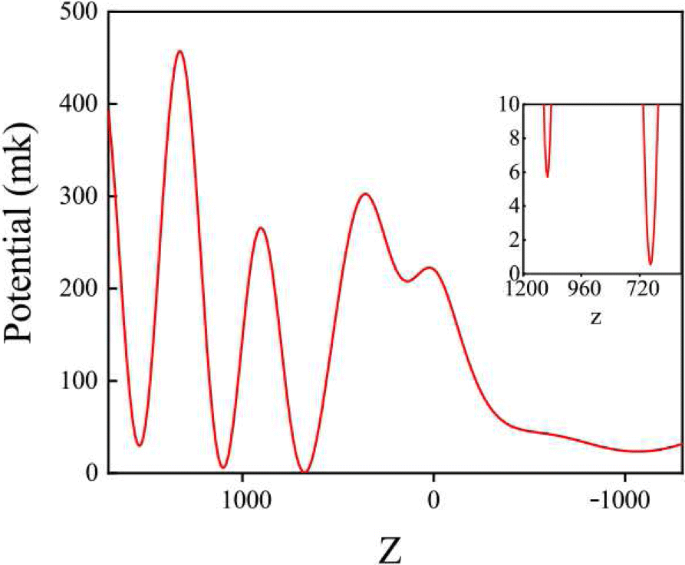
Potentiel de piégeage dans X -Z avion à Y =0. L'image d'insertion est la mise à l'échelle du potentiel de piégeage le plus bas

Sur la figure 4, nous savons que la position d'intensité la plus basse est au point P. Ici, la puissance incidente est définie sur P _i =120 mW, et le potentiel de piégeage est de 0,53 mK. Chen et al. a signalé que ⁸⁷ R b peut être piégé de manière stable avec un potentiel de piégeage de 2,02 mK [20]. En comparant ces paramètres, notre système de piégeage à désaccord bleu pourrait piéger une molécule de rhodamine avec un poids moléculaire d'environ 400. À la lumière de l'analyse ci-dessus, nous choisissons la position de piégeage au point (0, 0, 675 nm), et le schéma Le schéma d'une molécule piégée dans la structure est illustré à la Fig. 5.

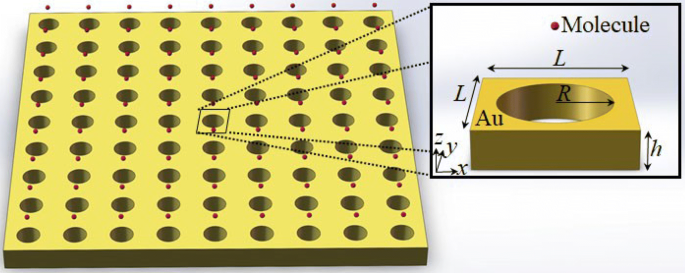
Schéma de principe d'une molécule piégée dans la structure

Couplage fort entre une structure et une molécule

Des molécules sont placées dans chaque unité de notre structure pour étudier l'interaction lumière-molécule à un régime de couplage fort. La molécule peut être traitée comme un dipôle dans les simulations FDTD. Nous ajoutons un dipôle au point minimum de potentiel P, qui se trouve à 275 nm de la surface, comme le montre la figure 3a. La polarisation du dipôle pourrait être le long du X -axe, le Y -axis, ou le Z -axe. La longueur d'onde de résonance de la molécule est de 707 nm (1,756 eV). Tout d'abord, nous considérons la polarisation du dipôle le long du Z -axe. Le spectre de transmission est également obtenu et le résultat est dans la Fig. 6.

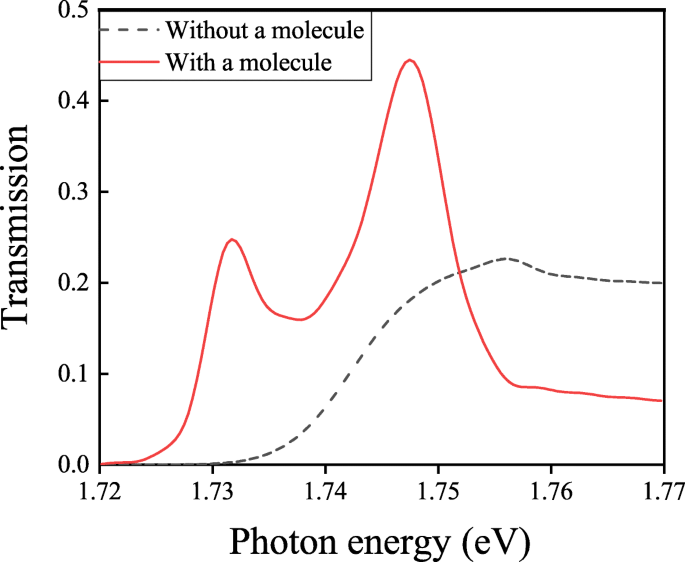
Les spectres de transmission avec et sans molécule sont piégés au point P

À titre de comparaison, le spectre de transmission de la structure sans molécule dans chaque unité est également tracé sur la figure 6. Conformément à la figure 6, nous pouvons observer deux pics de division dans le spectre de transmission de la structure avec une molécule, qui montre la Rabi se fendant en forme de ligne et présente le phénomène de couplage fort. La lumière incidente non seulement s'injecte à la surface de notre structure, mais rend également la molécule excitée. Les SPP excités par la lumière incidente se couplent à ceux excités par la molécule autour de la longueur d'onde de travail. Ces deux types de SPP se couplent et forment deux pics de division dans le spectre de transmission. L'allure de la courbe de transmission montre le phénomène de couplage fort. En générique, les fréquences de ces deux pics de division ω _± sont notés [36, 37] :

où ω ₀ est l'énergie à condition que la molécule isolée et la cavité soient supposées être en résonance, γ _c =4.08×10 ¹³ Hz [38] et γ _m =1.1×10 ¹⁴ Hz sont les taux de désintégration de la cavité plasmonique et de la molécule, respectivement, et g est la constante de couplage. Un couplage fort se produit pour g>0,5|γ _c −γ _m | et correspond à la formation d'un état habillé avec une durée de vie finie. Pour notre structure proposée, la constante de couplage g est de 144 meV, tandis que 0,5|γ _c −γ _m | est de 143 meV. Dans des travaux antérieurs, le fractionnement de Rabi noté Ω =|ω ₊ −ω ₋ | est dans le régime de 100 à 450 meV dans les structures à base de nanostructures hybrides J agrégat-métal ou molécule-métal [39, 40]. La division Rabi est liée à la force de couplage g , qui dépend de\(\sqrt {N/V}\), où N est le nombre de molécules et V est le volume de mode, respectivement [37]. Dans notre travail, il n'y a qu'une molécule dans chaque unité de la structure proposée et le volume de mode V est si grand que la division Rabi Ω est d'environ 16 meV, cette séparation est comparable à un couplage fort dans les nanostructures hybrides métal-semiconducteur [41] et le système de matériaux métal-2D [42]. Nous avons également étudié le couplage fort de la structure avec la polarisation de la molécule le long du X -axe et le Y -axe, respectivement. Les résultats de la simulation sont affichés sur la figure 7.

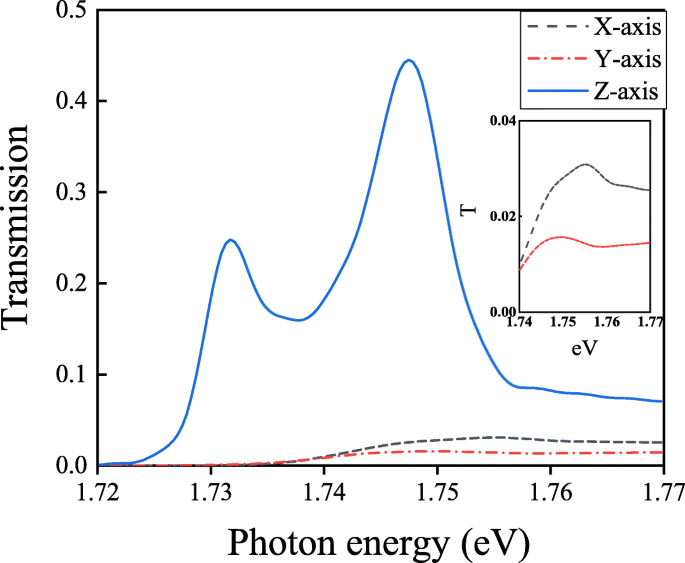
Spectres de transmission avec une molécule polarisée le long des directions X, Y et Z, respectivement

Sur la figure 7, deux pics de division (710 nm, 1,747 eV ; 717 nm, 1,717 eV) n'apparaissent dans la structure qu'avec la polarisation de la molécule le long du Z -axe. La molécule polarisée le long du X -axe ou le Y -axe montre un fort comportement collectif avant le couplage avec Au nanocavity ou Au nanohole array. Le comportement collectif S _k de la molécule polarisée le long du X -axe ou le Y -axe peut être calculé par la méthode des dipôles couplés [43] :

où k ₀ est le vecteur d'onde dans le vide, θ est l'angle entre deux dipôles, et r =n L , n =1, 2, 3... Ici, avec la condition de \( \lambda =\frac {L}{\sqrt {i^{2}+j^{2}}}\) (i , j =0, 1, 2,..., mais les deux i et j ne sont pas égaux à 0 en même temps), le comportement collectif est assez grand, ce qui présente une singularité dans l'Eq. (3) [35, 43]. Il présente un creux de résonance dans le spectre de transmission. Pour la molécule polarisée le long du X -axe ou le Y -axe, le comportement collectif est trop grand pour affaiblir le couplage entre la molécule et la cavité plasmonique. On ne voit que l'ordre de l'anomalie de Wood [35] avec l'ordre de (1, 1) dans le spectre de transmission autour de la longueur d'onde 707 nm (1.756 eV), le couplage fort n'a pu apparaître. Par conséquent, seule la molécule polarisée le long du Z -axe dans notre structure proposée peut générer le phénomène de couplage fort. Si la longueur d'onde de résonance de la molécule est modifiée, le couplage fort dans le système de piégeage désaccordé bleu peut également être obtenu par les étapes ci-dessous. Premièrement, selon la résonance de la molécule, la constante de réseau du réseau de nanotrous peut être fixée. Deuxièmement, la longueur d'onde de travail du système de piégeage à désaccord bleu peut également être déterminée, qui dépend de la constante de réseau du réseau de nanotrous métalliques. Troisièmement, la distribution du champ électromagnétique est obtenue pour trouver la position de piégeage. Enfin, nous plaçons la molécule à la meilleure position de piégeage pour calculer le spectre de transmission et la transmission avec la forme de raie de couplage fort peut être obtenue.

Conclusion

En résumé, nous concevons un système de piégeage plasmonique bleu désaccordé et étudions le phénomène de couplage fort entre une molécule quasi-simple et le système de piégeage. Dans les simulations FDTD, nous utilisons une source dipolaire comme molécule, et selon les distributions de champ électromagnétique, nous pouvons trouver la meilleure position pour piéger une seule molécule dans la structure. En calculant la transmission de la structure proposée lorsque la molécule a été piégée ou non, on constate qu'il y a deux pics de division dans le spectre de transmission lorsque la molécule est piégée dans la structure, alors qu'un seul pic est observé lorsque la molécule n'est pas piégée . Les deux pics de division indiquent que le couplage fort s'est produit. Par conséquent, nous pouvons concevoir le système de piégeage à désaccord bleu pour obtenir un couplage fort dans une structure nanoplasmonique, qui a des applications potentielles dans le traitement de l'information quantique.

Abréviations

FDTD :

Domaine temporel aux différences finies