La réponse photocourante extrêmement améliorée dans les nanofeuillets isolants topologiques à haute conductance

Introduction

C'est une tâche permanente de rechercher des matériaux avec une réponse photocourante plus élevée. La faible profondeur de pénétration de la lumière dans les matériaux à l'état solide fait que la réponse du photocourant est dominée par les porteurs de surface. Un matériau avec un support de surface plus abondant est un meilleur candidat comme photodétecteur. Pendant longtemps, les matériaux avec des rapports surface/volume élevés, tels que les nanofils, ont été largement étudiés [1–6]. Accompagné d'une large bande passante de photodétection, de matériaux de faible dimension avec une dispersion EK linéaire, tels que le graphène, [7, 8] des hétérostructures à base de graphène, [1–4], des dichalcogénures de métaux transitionnels (TMD) bidimensionnels et des matériaux topologiques, ont attiré une large attention [9–16].

Les rapports récents révèlent que la réponse photocourante signalée varie dans de larges plages [17–22]. On attribue intuitivement ces distributions à différentes conditions de croissance matérielle et expérimentales. La plupart des rapports concentrent leur attention sur l'ajustement des composants matériels. Les mécanismes intrinsèques potentiels sur ces distributions sont moins étudiés et discutés. Clarifier le mécanisme intrinsèque peut aider à améliorer les défauts potentiels et à optimiser considérablement les performances. On pense que la qualité de l'échantillon devrait être un facteur critique dominant la réponse photocourante [17–22]. En plus de la structure cristalline et de l'analyse des composants, existe-t-il d'autres méthodes physiques simples pour déterminer la qualité de l'échantillon ? Il a été porté à notre attention que la photoréactivité se répartit sur une large plage avec différentes résistances de feuille sur la base d'un certain nombre de rapports expérimentaux. Les processus de transport des paires électron-trou induits par les photons suivent les processus de diffusion dans les systèmes mésoscopiques à l'état solide, de sorte que la conductance du matériau serait un facteur critique pour dominer la réponse photocourante signalée. Cependant, cet effet n'est pas encore bien étudié, et les travaux expérimentaux connexes font défaut.

Pour identifier l'effet de la conductance sur la réponse du photocourant, nous avons systématiquement étudié la réponse du photocourant dans des nanofeuilles isolantes topologiques avec une conductivité différente. Le photocourant est linéaire avec l'intensité lumineuse et le photocourant est proportionnel au courant d'obscurité. Le photocourant plus élevé est observé dans la nanofeuille avec une conductivité plus élevée. La réactivité est proportionnelle à la conductance des nanofeuillets sur deux ordres. La réactivité est indépendante de l'intensité de la puissance lumineuse dans le vide, mais la réactivité diminue considérablement à faible intensité de puissance dans l'air. Le rapport de la sensibilité dans l'air à celle dans le vide est négativement proportionnel à l'inverse de l'intensité lumineuse. Ces comportements sont compris comme le photocourant statistique dans un système avec des molécules bloquées. La constante de temps diminue au fur et à mesure que l'épaisseur augmente. Ce comportement pourrait être compris comme le processus d'écoulement du courant d'uniformité. Les constantes de temps de charge et de décharge de différentes pressions sont déterminées. Une constante de temps plus longue est observée dans la basse pression atmosphérique. La réactivité, R , est linéaire avec la conductivité des nanofeuillets. Le R à V =0.1 V atteint 731 à des nanofeuillets avec une conductance plus élevée. Celles-ci sont supérieures à toutes les valeurs rapportées dans (Sb, Bi)₂ (Te, Se)₃ isolants topologiques et matériaux de faible dimension et seulement inférieurs à plusieurs hétérostructures rapportées.

Méthode expérimentale

Monocristaux de Sb₂ Voir₂ Te ont été cultivés dans un four à zone flottante chauffé par résistance (RHFZ) fait maison. Les matières premières de départ de Sb₂ Voir₂ Te ont été mélangés selon le rapport stoechiométrique. Au début, les mélanges stoechiométriques d'éléments de haute pureté Sb (99,995%), Se (99,995%) et Te (99,995%) ont été fondus à des températures de 700 ∼ 800 °C pendant 20 h, puis lentement refroidis à température ambiante dans un tube en verre de quartz sous vide. Le matériau résultant a été utilisé comme tige d'alimentation pour l'expérience RHFZ suivante. Après croissance, les cristaux ont ensuite été refroidis au four à température ambiante. Les cristaux au fur et à mesure de leur croissance ont été clivés le long du plan basal, produisant une surface argentée brillante semblable à un miroir, puis préparés pour d'autres expériences. Les spectres Raman, EDS et XPS confirment que le cristal est Sb₂ Voir₂ Te. La diffraction des rayons X montre des pics nets qui indiquent que le Sb₂ Voir₂ Le cristal de Te a une cristallinité et une uniformité élevées. Nos travaux antérieurs montrent que les paramètres physiques extraits de l'ARPES et de l'oscillation quantique SdH sont cohérents. Ceux-ci prennent en charge le Sb₂ Voir₂ Le cristal révèle une qualité et une uniformité élevées.

Le Sb₂ Voir₂ Les nanofeuillets ont été obtenus en exfoliant des cristaux en vrac à l'aide de ruban à découper et ont ensuite été dispersés sur l'isolant SiO₂ (300 nm)/n -Modèles Si avec circuits Ti/Au pré-configurés. Deux contacts métalliques en platine (Pt) ont ensuite été déposés sur le Sb₂ sélectionné Voir₂ Les nanofeuillets utilisant la technique du faisceau d'ions focalisés (FIB). La figure 1a–c montre les images SEM de trois Sb₂ Voir₂ Les nanofeuillets. L'épaisseur des nanofeuilles est déterminée par microscopie à force atomique, et l'épaisseur mesurée de trois nanofeuilles synthétisées était respectivement de 58 nm, 178 nm et 202 nm. La conductance de ces nanofeuillets a été mesurée par Keithley 4200-SCS. Le courant a été mesuré en fonction de la tension appliquée dans une méthode à deux sondes. Le je ⁺ et V ⁺ sont le même point de contact, et le I ⁻ et V ⁻ sont le même point de contact. Pour identifier l'effet de la conductance intrinsèque sur la réponse du photocourant, trois nanofeuillets avec une conductance différente ont été préparés pour la mesure du photocourant.

un , b , et c montrer les images SEM de trois Sb₂ Voir₂ Les nanofeuillets. L'épaisseur de la nanofeuille est mesurée par AFM. Deux contacts de Pt ont été déposés sur une nanofeuille pour mesurer le photocourant. d , e , et f révèlent la relation tension-courant, et elle est linéaire. Cela indique le contact ohmique entre les électrodes Pt et Sb₂ Voir₂ Les nanofeuillets

Résultats et discussion

La figure 1d–f révèle une relation tension-courant linéaire. Cela indique la caractéristique métallique et les contacts ohmiques entre les électrodes de Pt et les nanofeuillets. La conductance mesurée, G , sont 4 × 10 ⁻⁵ , 0,006 et 7 × 10 ⁻⁵ (S) pour les nanofeuillets avec des épaisseurs de 202, 178 et 58 nm, respectivement. La conductivité est supérieure à 1000 (S/m), ce qui prend en charge la qualité cristalline extrêmement élevée de nos nanofeuilles.

La figure 2a–c montre les courants mesurés en fonction de l'intensité lumineuse. La figure 2d–f révèle que le courant mesuré est proportionnel à l'intensité lumineuse [27, 28]. La relation pourrait être exprimée par I _sur =β P ^α +Je _désactivé , où le I _sur est les courants mesurés avec la lumière, I _désactivé est les courants mesurés sans lumière, β est une constante liée à la réponse photocourante, P est l'intensité de la puissance lumineuse, et α est une constante liée à la condition d'éclairage entre les appareils et la lumière. Il convient de noter que le plus grand I _sur est observé dans la nanofeuille avec un I plus grand _désactivé . Le photocourant, I _ph , est défini comme I _sur −Je _désactivé . Le tableau 1 répertorie le résultat de l'ajustement. Cela montre que α ≈1 pour toutes les nanofeuilles avec différentes épaisseurs, et qui prend en charge les caractéristiques optiques cohérentes de ces nanofeuilles. Il convient de noter que β /G est de 1,1 × 10 ⁵ ±0,2×10 ⁵ (A /WS) pour toutes les nanofeuillets. Cela indique que le photocourant observé est proportionnel à la conductance effective. Cette découverte confirme qu'outre la géométrie du système et la structure de la bande de matériau, la conductance effective des nanofeuillets serait également un facteur critique dominant la réponse du photocourant.

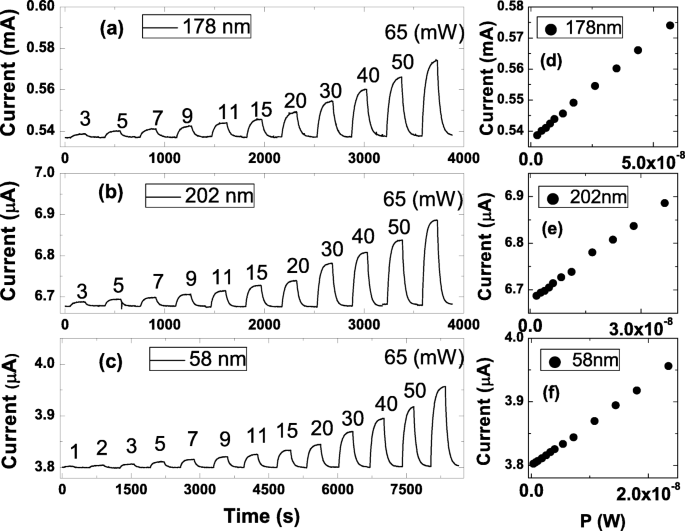
un , b , et c montrent les courants mesurés en fonction de l'intensité de la puissance lumineuse dans trois échantillons d'épaisseurs différentes. d , e , et f révèlent que les courants mesurés sont proportionnels à l'intensité lumineuse. Il vient à notre attention que le plus grand I _sur est observé dans la nanofeuille avec un I plus grand _désactivé

Le Je _ph provient de paires électron-trou induites par l'interaction entre les photons injectés et les nanofeuillets. Les électrons et les trous induits circulent dans des directions opposées sous une polarisation électrique appliquée. Le I efficace _ph est proportionnelle à la tension appliquée et à la quantité de paires électron-trou. Plus de photons injectés conduisent à plus de paires électron-trou. La profondeur de pénétration de la lumière est courte et faible en fonction de l'intensité de la puissance lumineuse. Il est rapporté que la profondeur de pénétration de la lumière est d'environ 20 nm dans les isolants topologiques, ce qui est inférieur à l'épaisseur de nos nanofeuilles [23, 24]. Le Je _ph devrait être indépendant de l'épaisseur de la nanofeuille lorsque l'épaisseur est supérieure à la profondeur de pénétration de la lumière. La surface de la nanofeuille se répartit dans un facteur 3, mais le I observé _ph s'étale sur une différence de deux ordres. En dehors des paires électron-trou induites effectives, les différents I observés _ph doit provenir de propriétés intrinsèques. Afin d'exclure les effets de géométrie extrinsèque sur le I _ph et déterminer quantitativement les performances de ces nanofeuillets, la réactivité, R , est calculé à l'aide de l'équation suivante :

où P et S sont respectivement l'intensité lumineuse et la surface effective.

La figure 3 montre R en fonction de l'intensité de la puissance lumineuse, différente de la plupart des rapports signalés que le R diminue considérablement à mesure que l'intensité de la puissance lumineuse augmente dans les isolants topologiques à base de Bi et les matériaux de faible dimension [25, 26]. Nos résultats montrent que le R et G sont indépendants de l'intensité lumineuse dans le vide. Cela soutient en outre que la profondeur de pénétration de la lumière devrait être plus courte que l'épaisseur de la nanofeuille dans nos conditions expérimentales. Le plus grand R est observée dans la nanofeuille avec une conductance plus élevée. Cela confirme que la photoréponse plus élevée observée provient des caractéristiques de transport intrinsèques et non de la géométrie de la nanofeuille ou des conditions expérimentales.

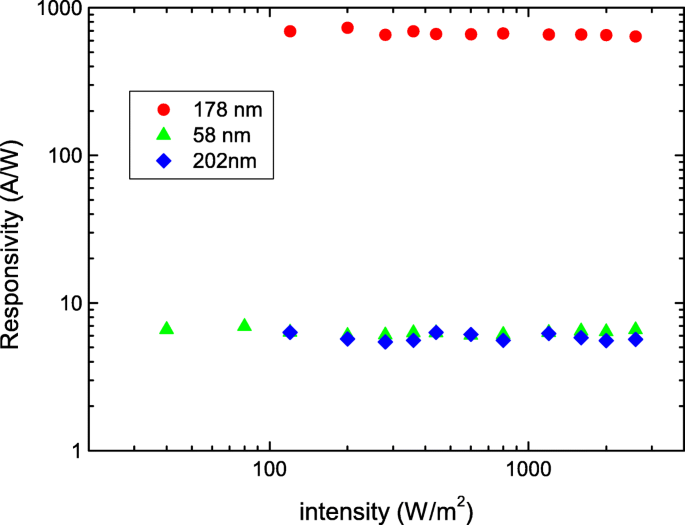
La réactivité de trois Sb₂ Voir₂ Les nanofeuillets. Il révèle une faible dépendance de l'intensité de la puissance lumineuse à la réactivité. La réactivité plus élevée est observée dans la nanofeuille avec une conductivité plus élevée

Comme le montre la figure 1, la relation tension-courant linéaire soutient que les nanofeuillets révèlent un comportement métallique. Les paires électron-trou induites par la lumière se déplaceraient vers deux contacts d'électrode en raison de la polarisation de tension appliquée [27-29]. Suivant la loi d'Ohm, le photocourant associé pourrait être déterminé par la relation I _ph =V G où V est la tension de polarisation appliquée entre deux électrodes. Le Je _ph est proportionnel au G .

La figure 4 révèle le R en fonction du G dans un tracé log-log. Les points de données de Sb₂ Voir₂ Te sont les résultats mesurés dans ce travail, et les points de données de Sb₂ SeTe₂ sont extraits de nos travaux antérieurs dans les mêmes conditions de croissance cristalline et configurations de mesure [27]. L'épaisseur de Sb₂ SeTe₂ les nanofeuillets mesurent environ 180 nm. La longueur d'onde est de 532 nm. Les deux Sb₂ Voir₂ Te et Sb₂ SeTe₂ montrer que R est indépendant de l'intensité lumineuse. Ces points de données suivent la tendance de la ligne de points sur une large plage de conductance de la nanofeuille. Cela prend en charge que R est proportionnel au G , ce qui est cohérent avec notre proposition.

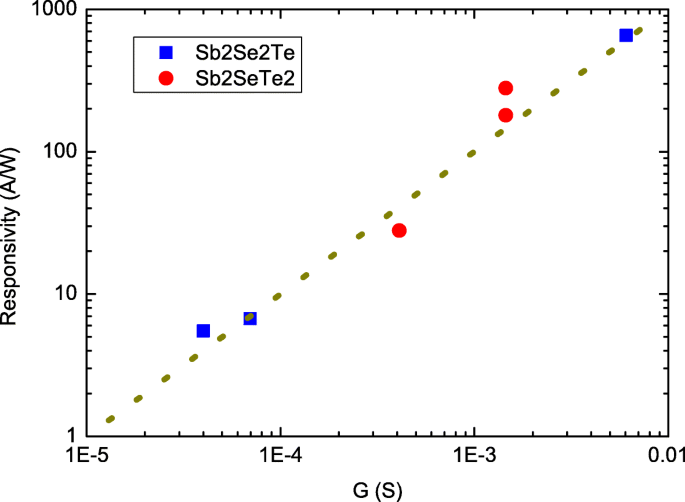
La réactivité en fonction de la conductance des nanofeuillets. Il montre que la réactivité est proportionnelle à la conductance de la nanofeuille. Le Sb₂ SeTe₂ les données proviennent de nos valeurs déclarées

Un système avec une réponse photocourante plus élevée est grandement préféré pour les applications potentielles. En plus de rechercher de nouveaux matériaux ou systèmes avec une structure de bande et une bande interdite spécifiques, un traitement approprié sur un système serait également une méthode appropriée pour améliorer la photoréponse. Nos résultats expérimentaux soutiennent que la conductance électrique intrinsèque serait un facteur critique pour optimiser la réponse photocourante. Ceci pourrait être réalisé grâce à des conditions de croissance appropriées. Comme le montre la figure 4, le photocourant est amélioré de 2 ordres grâce au réglage de la conductance. Cette étude pourrait guider d'autres chercheurs dans la construction d'une ligne directrice appropriée dans la sélection d'un meilleur système pour d'autres études expérimentales grâce à un simple test électrique.

Le R et détective à V =0.1V atteint 731 et 2,6×10 ¹⁰ à la nanofeuille avec une conductivité plus élevée. Ces photoréponses sont supérieures à toutes les valeurs rapportées dans (Sb, Bi)₂ (Te, Se)₃ isolants topologiques et matériaux de faible dimension [27, 28] et seulement inférieur à plusieurs hétérostructures rapportées. Récemment, les matériaux de faible dimension ont attiré une grande attention dans le domaine du photocourant. Il vient à notre attention que la conductivité signalée dans ces matériaux de faible dimension est extrêmement élevée. Ceci est cohérent avec notre résultat expérimental selon lequel la conductivité serait un facteur critique dominant la réponse photocourante.

La figure 5 illustre R en fonction de l'intensité lumineuse dans le vide et l'atmosphère. Il vient à notre attention le R diminue drastiquement lorsque l'intensité lumineuse est inférieure à 500 Wm ⁻² en atmosphère. Cela confirme que ce R décroissant à faible intensité lumineuse dans l'atmosphère pourrait provenir de l'influence de la molécule adsorbée à la surface de notre Sb₂ Voir₂ La nanofeuille.

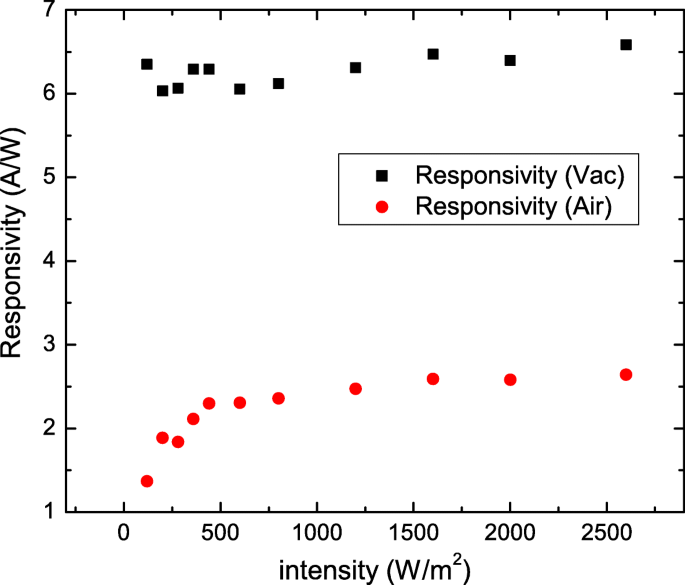
Réactivité et gain photoconducteur en fonction de l'intensité de la puissance lumineuse à une longueur d'onde de 532 nm. La réactivité est une faible dépendance à l'intensité de la puissance lumineuse dans le vide. La réactivité diminue à mesure que l'intensité de la puissance lumineuse diminue dans l'atmosphère lorsque l'intensité de la puissance lumineuse est inférieure à 500 W /m ²

La photoréponse serait extrêmement sensible à l'état de la surface de l'échantillon. En plus de la réduction de la zone de réponse efficace, les défauts de surface et l'oxydation peuvent réduire la mobilité et la durée de vie des porteurs.

Récemment, il a été rapporté que des molécules adsorbées à la surface de Bi₂ Se₃ les isolants topologiques plient la structure et conduisent à un 2DEG supplémentaire. Ce 2DEG induit améliorerait la mobilité effective des porteurs [30]. Un système avec une mobilité des porteurs plus élevée pourrait réduire le temps de transit des porteurs et produire un photocourant plus élevé. D'autre part, la mobilité améliorée des porteurs doit être indépendante de l'intensité de la puissance lumineuse. Ceux-ci soutiennent que le R observé la suppression provient principalement de la zone de brillance effective, et non des caractéristiques de transport intrinsèques. Ainsi, on pense que la baisse de R dans l'air à faible intensité lumineuse devrait être davantage lié à l'effet d'ombre moléculaire adsorbé qu'à l'effet de relaxation intrinsèque du porteur complexe.

La définition de la réactivité est le rapport entre le porteur induit et les photons incidents, et elle pourrait également être exprimée sous la forme \(R=\eta \frac {q}{hf},\) où q , hf , et η sont respectivement la charge du porteur, la photo-énergie et l'efficacité quantique. Le η est directement liée aux propriétés du matériau et à la longueur d'onde de la lumière. Pour exclure d'autres effets extrinsèques et intrinsèques et optimiser l'effet d'ombre de la molécule, le R (un je r )/R (v un c ) est tracé en fonction de l'intensité de la puissance lumineuse. Comme le montre la figure 6, le rapport augmente à mesure que l'intensité de puissance augmente et sature progressivement à une intensité de puissance élevée.

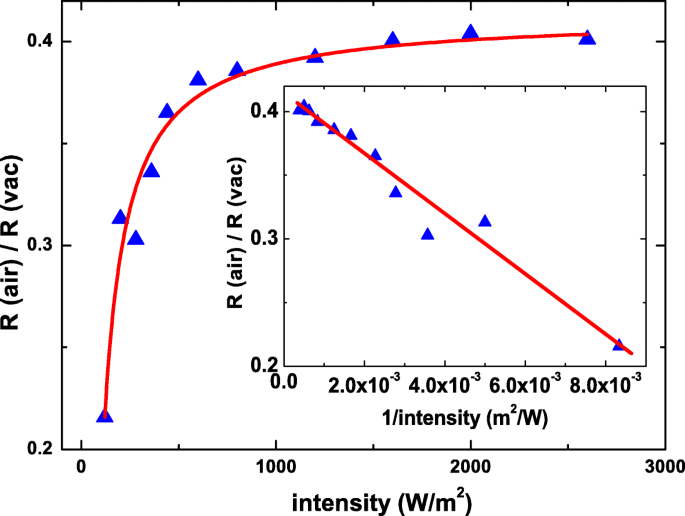
Le rapport de la sensibilité dans l'air à celle dans le vide en fonction de l'intensité de la puissance lumineuse. Les points de données vont bien avec la prédication théorique. L'encart montre que le rapport de la réactivité dans l'air à celle dans le vide est négativement proportionnel à l'inverse de l'intensité de la puissance lumineuse

Nous proposons un modèle dont le nombre de photons incidents est Y , le m les photons interagissent avec la matière, et n les photons sont bloqués par des molécules adsorbées à la surface. C'est-à-dire Oui =m +n . Le Z est le nombre moyen de porteurs de photocourant induit par un photon. Dans l'intensité lumineuse extrêmement faible, le nombre de photo est bien inférieur à l'unité moléculaire totale, le photocourant effectif doit suivre le calcul statistique, et le résultat confirme que l'efficacité quantique, η , pourrait être exprimé sous la forme

Ce calcul statique soutient que le photocourant effectif serait fortement lié à l'intensité de la puissance lumineuse dans la limite de la faible intensité de la puissance lumineuse et du temps de relaxation long ; le nombre de photons peut être plus petit que le "créateur de porte-photos". Le photocourant effectif peut être exprimé par

Le Y est directement proportionnel à l'intensité lumineuse. Le R (un je r )/R (v un c ) est négativement proportionnelle à l'inverse de Y et dépend faiblement du Y dans la situation du Y n . Comme le montre la figure 6, cela révèle clairement que les points de données mesurés vont bien avec l'équation théorique, et l'encart montre que les points de données sont négativement proportionnels à l'inverse de l'intensité de la puissance lumineuse. Ceux-ci soutiennent que la chute de photocourant observée provient principalement de l'effet d'ombre des molécules adsorbées sur la surface. Le \(\frac {R(air)}{R(vac)}\) est d'environ 0,4 à haute intensité de puissance et cela indique que la surface recouvre de 40 % des molécules adsorbées.

L'encart en bas à gauche de la figure 7 montre le photocourant en fonction du temps. Le processus de facturation pourrait être décrit par le e ^{−t /k} , où k est une constante de temps caractéristique. Notre résultat expérimental révèle que le photocourant mesuré s'accorde bien avec la ligne de montage. L'encart en haut à droite montre la constante de temps de charge extraite en fonction de l'épaisseur. Il révèle que la constante de temps diminue à mesure que l'épaisseur augmente. Ce comportement pourrait être compris comme le processus d'écoulement de courant d'uniformité [27, 28]. D'autre part, les constantes de temps de charge et de décharge de différentes pressions atmosphériques sont déterminées. Il montre que la constante de temps de charge est à peu près la même que les constantes de temps de décharge, et une constante de temps plus longue est observée dans la basse pression atmosphérique.

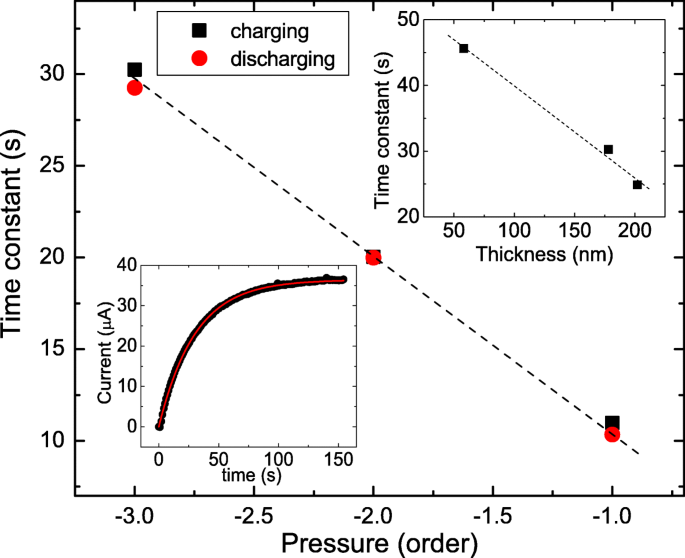
L'encart en bas à gauche montre le photocourant en fonction du temps dans le processus de charge, et il va bien avec la ligne de montage. L'encart en haut à droite montre la constante de temps de charge en fonction de l'épaisseur. La constante de temps de charge et de décharge en fonction de la pression

Conclusion

Le photocourant a été réalisé dans le Sb₂ Voir₂ L'isolant topologique avec une conductance différente à une longueur d'onde de 532 nm. Le photocourant est linéaire avec l'intensité lumineuse et le photocourant est proportionnel au courant d'obscurité. Un photocourant plus élevé est observé dans la nanofeuille avec une conductance plus élevée. La réactivité est proportionnelle à la conductivité des nanofeuillets. La réactivité est indépendante de l'intensité de la puissance lumineuse dans le vide, mais la réactivité diminue considérablement à faible intensité de puissance dans l'air, contrairement à la plupart des résultats rapportés. Le rapport de la sensibilité dans l'air à celle dans le vide est négativement proportionnel à l'inverse de l'intensité lumineuse. Ces comportements sont compris comme le photocourant statistique dans un système avec des molécules bloquées. Suivant le modèle théorique, la surface est recouverte de molécules adsorbées à 40 % dans l'air. La constante de temps diminue au fur et à mesure que l'épaisseur augmente. Ce comportement pourrait être compris comme le processus d'écoulement du courant d'uniformité. Les constantes de temps de charge et de décharge de différentes pressions sont déterminées. Une constante de temps plus longue est observée dans la basse pression atmosphérique. Le R et détective à V =0.1V atteint 731 et 2,6×10 ¹⁰ à la nanofeuille avec une conductivité plus élevée. Celles-ci sont supérieures à toutes les valeurs rapportées dans (Sb, Bi)₂ (Te, Se)₃ isolants topologiques et matériaux de faible dimension et seulement inférieurs à plusieurs hétérostructures rapportées.

Abréviations

ARPES :

Spectroscopie de photoémission résolue en angle

EDS :

Spectroscopie à rayons X à dispersion d'énergie

SdH :

Shubnikov-de Haas

XPS :

Spectroscopie photoélectronique aux rayons X