Observation d'oscillations de type Aharonov-Bohm-Like dépendant du niveau de Landau dans un isolant topologique

Introduction

L'interférence Aharonov-Bohm (AB) provient de l'interférence de la fonction d'onde porteuse dans une boucle qui peut être un anneau à motifs [1, 2], une structure géométrique matérielle [3–6, 8–11] ou une trajectoire de transport de porteuse [12]. Le champ magnétique, B , à travers la boucle induira un déphasage de la fonction d'onde porteuse qui conduit à des oscillations d'interférence périodiques de la fonction d'onde. Cette période d'oscillation est sensible aux caractéristiques de transport des porteurs, telles que la longueur de cohérence et la mobilité des porteurs [3, 12]. L'interférence quantique est un excellent outil pour détecter les caractéristiques de transport de matière et comprendre les mécanismes intrinsèques. En raison de la courte longueur de cohérence de la porteuse et du petit flux quantique, l'interférence quantique est principalement signalée au niveau des nanofils à haute mobilité ou des nano-anneaux à motifs à faible B [3-6, 8-11]. Rapports sur un système macroscopique à haut B sont rares. Les travaux sur l'interférence quantique AB à haut B sont moins étudiés et le mécanisme associé est moins compris.

Dans ce travail, des oscillations quantiques ont été réalisées dans un BiSbTe₃ macroflocon d'isolant topologique à haut B . En plus de l'oscillation de Shubnikov-de Haas (SdH), l'oscillation de type Aharonov-Bohm (ABL) a été observée. La période d'oscillation ABL est B -dépendant et différent de l'oscillation AB traditionnelle, dont la période d'oscillation est indépendante de B . La période d'oscillation ABL observée est constante à chaque niveau de Landau (LL), qui est déterminé à partir de l'oscillation SdH. Les périodes d'oscillation plus courtes sont observées à des LL plus faibles. La période d'oscillation est proportionnelle à la racine carrée de la LL aux températures. Le rapport de la période d'oscillation ABL à la masse effective est une faible dépendance LL. L'oscillation ABL dépendante de LL pourrait provenir de la masse effective dépendante de LL.

Méthode expérimentale

La condition de croissance du BiSbTe₃ monocristal est le même que nos précédents travaux sur les isolants topologiques [13-16]. Nos travaux antérieurs ont démontré qu'une TI avec une uniformité extrêmement élevée peut être obtenue en utilisant la méthode RHFZ [13–16]. Les spectres Raman, EDS et XPS ont prouvé que le cristal est BiSbTe₃ . Le BiSbTe₃ des flocons de monocristaux ont été obtenus en utilisant la méthode du scotch. La géométrie des flocons clivés mesure environ 3 mm de longueur, 2 mm de largeur et 170 μ m d'épaisseur. Les mesures de magnétotransport ont été effectuées en utilisant la technique standard à six sondes dans un appareil commercial (Quantum Design PPMS) avec un B jusqu'à 14 T. Le B a été appliqué perpendiculairement à la grande surface clivée. Les points de données sont pris pour 100 Gauss dans une région de champ magnétique comprise entre 6 et 14 T en mode de champ magnétique permanent, au lieu du mode de champ magnétique de balayage.

Résultats et discussion

La figure 1 montre les magnétorésistances (MR) en fonction de B . Le R (14T)/R (0T) atteint 10 et est supérieur à la plupart des valeurs rapportées dans Bi _x Sb _2−x Te _y Se _3−y isolants topologiques [17-23, 23-33]. Les études théoriques et expérimentales soutiennent que le rapport MR est proportionnel à la mobilité du porteur [34], Le rapport MR élevé mesuré soutient la haute qualité de notre BiSbTe₃ goûter. L'encart en haut à gauche révèle le d R /d B en fonction de 1/B . Il révèle que les oscillations périodiques et les pics et creux d'oscillation sont au même B à 2 et 8 K. C'est ce qu'on appelle l'oscillation SdH qui provient d'un système bidimensionnel. La période d'oscillation SdH correspond au vecteur moment de Fermi, k _f . L'encart en bas à droite montre la transformée de Fourier rapide (FFT) de l'oscillation SdH. Un pic pointu à 48 T est observé à la fois pour 2 et 8 K. Suite à la relation d'Onsager, on pourrait estimer k _f à \(F=\frac {\hbar k_{f}^{2}}{2e}\), où F est la fréquence d'oscillation SdH. Le F =48 T mène au k _f =3.8Å ⁻¹ , ce qui est cohérent avec la valeur observée de l'ARPES d'un lot différent du même cristal et des valeurs rapportées dans la littérature [35]. Cela soutient la haute qualité et l'uniformité de notre BiSbTe₃ cristal. En plus de l'oscillation SdH, l'encart en haut à gauche révèle des oscillations avec une courte période. Pour supprimer l'influence de l'oscillation SdH et extraire les caractéristiques d'oscillation, le d ² R /d B ² est effectuée.

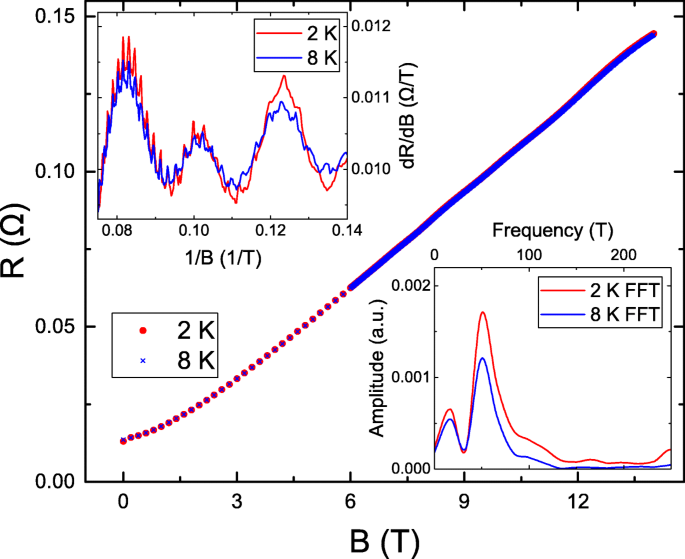
La magnétorésistance en fonction des champs magnétiques à 2 et 8 K. L'encart en haut à gauche montre le d R /d B en fonction des champs magnétiques inverses. Il révèle des oscillations périodiques. L'encart en bas à droite montre la transformée de Fourier rapide de l'oscillation SdH et un pic net à 48 T pour 2 et 8 K

La figure 2 montre le d R /d B et d ² R /d B ² en fonction de B à 2 et 8 K. Les lignes de points marquent les pics d'oscillation en d ² R /d B ² , et les longs tirets correspondent à B de LL qui sont déterminés à partir de la fréquence d'oscillation SdH extraite. Les oscillations périodiques sont similaires à l'oscillation AB. La période d'oscillation AB est exprimée par \(\Delta B =\frac {\Phi }{A}\). Φ est le quantum de flux, où \(\frac {h}{e}\), et A est la zone géométrique bouclée par les trajectoires des porteurs d'horloge et d'anti-horloge dans une structure confinée. En raison du faible quantum de flux, l'oscillation AB est principalement observée dans le confinement par des nanostructures artificielles [1, 2], telles que des nano-anneaux et des nanofils [3–11]. Récemment, il a été rapporté que la trajectoire de diffusion élastique du porteur pourrait former une série de boucles fermées connectées dans un système macroscopique. A B le flux à travers ces boucles induirait un déphasage de la fonction d'onde porteuse et conduirait à des oscillations ABL périodiques [12]. La longueur de diffusion élastique extraite est d'environ 150 nm, ce qui correspond à la période d'oscillation avec 0,02 T et est conforme à notre observation expérimentale.

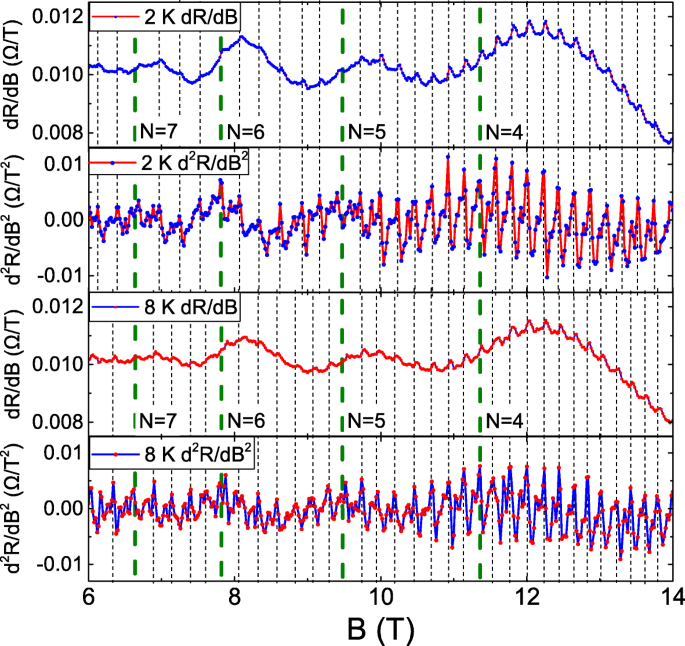
Le d R /d B et d ² R /d B ² en fonction de B à 2 et 8 K. Il montre des oscillations périodiques et la période d'oscillation est la dépendance du niveau de Landau

En suivant les lignes pointillées de la Fig. 2, on peut noter que la période d'oscillation est constante à chaque LL et la période d'oscillation est plus courte aux LL plus faibles. Ce comportement est différent de l'oscillation AB traditionnelle. Pour extraire et déterminer ces périodes d'oscillation, la FFT est effectuée à différents LL. La figure 3 montre la FFT à différentes LL à 2 et 8 K, et elle révèle clairement la fréquence d'oscillation la plus élevée à des LL inférieures à 2 et 8 K.

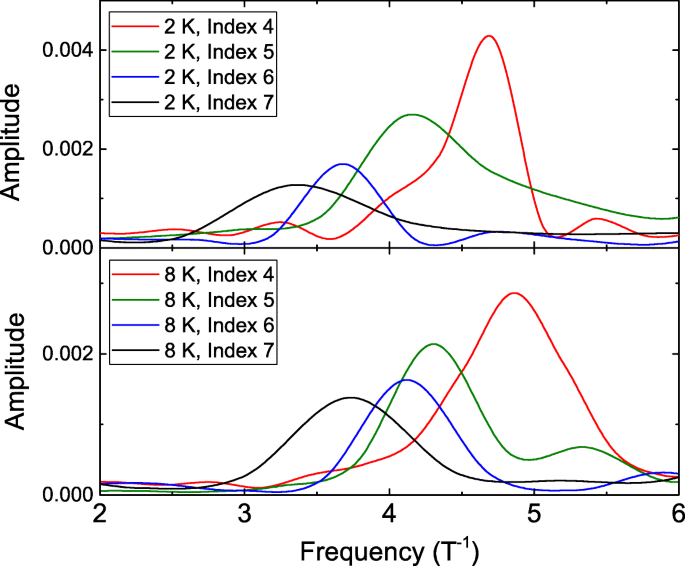
La transformée de Fourier rapide du d R /d B à différents niveaux et températures de Landau. Le pic de fréquence d'oscillation plus élevé est observé à des niveaux de Landau inférieurs

Une oscillation ABL similaire dépendante de LL est rapportée au régime de Hall quantique entier dans un gaz d'électrons bidimensionnel semi-conducteur [36, 37]. Il a été interprété soit comme une interférence constructive d'électrons unidimensionnels voyageant le long des canaux de bord, soit comme une interférence d'ondes quantiques des électrons de bord. Le chemin de transport des porteurs dans différents canaux périphériques conduit à différentes zones effectives dans un motif confiné et éventuellement à différentes périodes d'oscillation ABL dans les canaux périphériques à différentes LL [38–40]. D'autres études sur les interféromètres électriques Fabry-Perot en régime Hall quantique entier et fractionnaire révèlent que la période d'oscillation ABL est liée à la période de flux par \(\frac {\Phi }{f}\), où f est le LL entièrement occupé dans les étranglements. La période d'oscillation devrait être \(\frac {\Phi }{A f}\), où A est l'aire géométrique de la forme confinée [41, 42].

Le tableau 1 répertorie les périodes d'oscillation extraites de la FFT à différentes LL et températures. L'analyse révèle que le rapport de la période d'oscillation à la racine carrée de LL est constant à chaque température. Ceci est différent du comportement de l'interféromètre de Fabry-Pérot dans lequel l'oscillation est inversement proportionnelle aux LL [41, 42]. D'autre part, l'interférence électrique de Fabry-Pérot provient du couplage de trajectoires de porteurs entre différentes LL de l'intérieur et de l'extérieur d'un motif confiné [37]. L'oscillation est fortement liée à la géométrie à motifs. Il n'y a pas de motifs artificiels à la surface de nos échantillons, et il ne devrait pas y avoir de canaux de couplage appropriés entre les différentes LL. De plus, les tailles géométriques de nos échantillons sont à l'échelle millimétrique et la période d'oscillation AB associée serait trop petite pour être détectée. Malgré ces différences par rapport aux travaux existants, nous pensons qu'en dehors de l'aire géométrique et de la longueur de cohérence du porteur, la caractéristique intrinsèque du porteur pourrait jouer un rôle critique sur l'oscillation ABL dépendante de la LL [3, 43].

En suivant la théorie de Lifshitz-Kosevich (LK), on peut extraire des paramètres caractéristiques des transporteurs dans l'état de surface de l'isolant topologique, et la dépendance en température de l'amplitude de l'oscillation SdH est exprimée sous la forme

où \(\lambda (T/B) =(2\pi ^{2}k_{B}Tm_{cyc})/(\hbar eB)\). La figure 4 montre l'amplitude d'oscillation SdH normalisée extraite en fonction de la température à différentes LL. Elle s'accorde bien avec la théorie LK et révèle des tendances différentes selon les LL. Les résultats d'ajustement confirment que le m _cycler =0.152m ₀ ,0.170m ₀ ,0.185m ₀ , et 0,191m ₀ , où m ₀ est la masse de l'électron libre, pour N =4, 5, 6 et 7, respectivement. Ces valeurs sont cohérentes avec les masses effectives rapportées dans les isolants topologiques [21, 22]. Cette masse effective dépendante du niveau de Landau a été récemment observée dans le semi-métal 3D Dirac ZrTe₅ [44]. Cependant, l'origine de la masse effective dépendant du champ magnétique n'est pas encore claire. Il nécessite une étude plus approfondie pour clarifier le mécanisme intrinsèque. La masse effective différente dévierait directement la caractéristique intrinsèque de transport de porteur à la surface de Fermi, telle que la vitesse de Fermi, qui est directement liée à la longueur de cohérence de phase de porteur. La masse effective plus élevée conduirait à une longueur de cohérence plus faible qui correspond à la période d'oscillation de type AB plus longue. Ceci est qualitativement cohérent avec notre observation expérimentale. Comme le montre le tableau 1, le rapport de la période d'oscillation de type AB à la masse effective montre une faible dépendance LL. La masse effective dépendante du niveau de Landau pourrait être l'un des effets intrinsèques qui conduisent à la période d'oscillation dépendante de la LL.

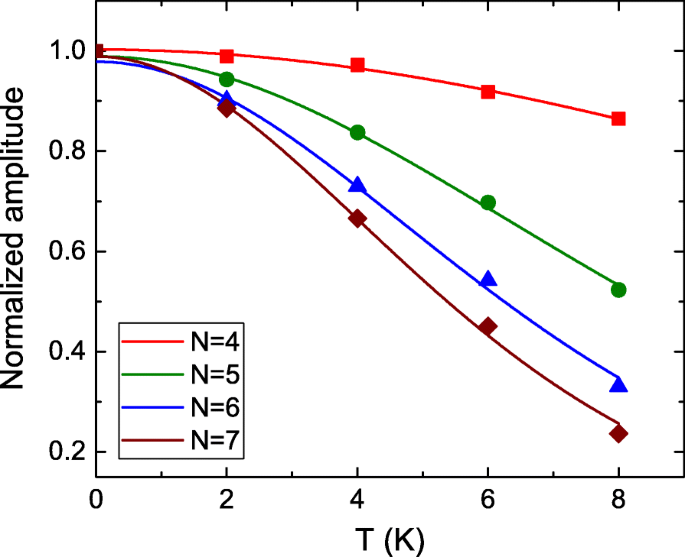
L'amplitude d'oscillation SdH normalisée extraite en fonction de la température à différents niveaux de Landau. Il s'accorde bien avec la théorie LK et révèle une tendance différente à différents niveaux de Landau

LL est une caractéristique de transport d'un système bidimensionnel. Cela indique que l'oscillation dépendante de LL pourrait provenir du porteur de l'état de surface dans les TI. La phase Berry est une caractéristique des transporteurs. L'extraction de la phase Berry pourrait aider à identifier la source de ces oscillations AB périodiques dépendantes de LL. Nous définissons l'indice d'oscillation AB en divisant le B correspondant des pics d'oscillation en d B /d B par la période d'oscillation associée dans la LL. Il révèle que le nombre d'indices des pics d'oscillation en d B /d B correspond à N +0.25, où N est un nombre entier, pour toutes les oscillations dans différentes LL et températures. Cela confirme en outre que la période d'oscillation AB est liée aux LL. La figure 5 montre que les nombres d'indices d'oscillation AB sont proportionnels à B à différentes LL et températures. L'interception est de 0,25, ce qui indique un déphasage de 0,5 dans le tracé de l'oscillation AB. Cela prend en charge la phase Berry est π et les oscillations AB observées pourraient être la caractéristique de transport de porteurs de l'état de surface dans notre BiSbTe₃ isolant topologique [45].

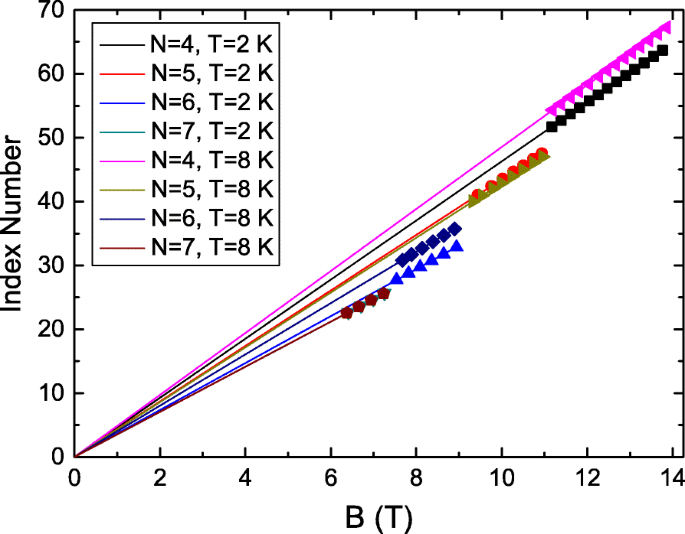
L'indice d'oscillation AB en fonction de B à différents niveaux et températures de Landau. L'interception est de 0,25, ce qui indique un déphasage de 0,5 dans le tracé de l'oscillation AB. Cela prend en charge la phase Berry est π

Conclusion

Nous avons rapporté les oscillations quantiques dans un BiSbTe₃ macroflocon d'isolant topologique. En plus de l'oscillation Shubnikov-de Haas (SdH), elle révèle une oscillation de type Aharonov-Bohm (ABL). La période d'oscillation ABL est B -dépendant. La période d'oscillation ABL est constante à chaque niveau de Landau (LL). Les périodes d'oscillation plus courtes ont été observées à des LL inférieures, qui ont été déterminées par l'oscillation SdH. La période d'oscillation est proportionnelle à la racine carrée de la LL à différentes températures. Le rapport de la période d'oscillation ABL à la masse effective est faiblement dépendant de LL. L'oscillation ABL dépendante de LL pourrait provenir de la masse effective dépendante de LL.

Disponibilité des données et des matériaux

Les ensembles de données générés et/ou analysés au cours de la présente étude sont disponibles auprès des auteurs correspondants sur demande raisonnable.

Abréviations

EDS :

Spectroscopie à rayons X à dispersion d'énergie

XPS :

Spectroscopie photoélectronique aux rayons X

ARPES :

Spectroscopie de photoémission résolue en angle

SdH :

Shubnikov-de Haas