La bifurcation de susceptibilité magnétique dans l'isolant topologique Sb2Te3 dopé Ni avec ordre antiferromagnétique accompagné d'un alignement ferromagnétique faible

Introduction

Les isolants topologiques tridimensionnels possèdent un état de surface sans faille à dispersion linéaire qui est protégé par une symétrie d'inversion du temps [1, 2]. L'état de surface topologique est constitué de fermions de Dirac filtrés par spin. Cette texture hélicoïdale de spin de l'état de surface topologique a attiré beaucoup d'attention en raison de ses applications électriques et liées au spin [3,4,5,6,7,8,9,10,11,12,13,14 ,15,16,17,18,19,20]. Outre les caractéristiques exotiques intrinsèques, l'introduction de l'aimantation dans l'isolant topologique modifiera l'électronique. Cette interaction d'échange entre l'électron de conduction et les atomes magnétiques brise la symétrie d'inversion du temps et cela ouvre une brèche de l'état de surface de Dirac. Le fermion de Dirac à l'état de surface devient massif [1, 2, 21] et conduit à de nombreuses propriétés intéressantes, telles que l'effet Hall anormal quantique, [22, 23] l'effet magnéto-électrique topologique [24], l'accordabilité du mode de bord chiral [ 25, 26] et tressage Majorana [27,28,29]. Le porteur de l'état de surface topologique domine ces propriétés magnétoélectriques. De nombreux travaux expérimentaux ont été réalisés dans des couches minces dopés Mn, Cr et V (Bi, Sb)\(_{2}\)Te\(_{3}\) pour réaliser la prédiction théorique [30]. La plupart de ces études se sont principalement concentrées sur les propriétés de transport électrique-magnéto, telles que l'effet Hall anormal quantique, l'effet magnétoélectrique topologique et les applications associées. En raison du faible signal de magnétisme dans un film mince avec un isolant topologique faiblement dopé aux éléments magnétiques, de rares études sur les propriétés magnétiques intrinsèques des aimants dopés ont été rapportées dans des isolants topologiques dopés aux éléments magnétiques et le couplage magnétique associé n'est pas bien exploré. Pour comprendre les nouvelles propriétés physiques intrinsèques de l'isolant topologique dopé à l'élément magnétique, en particulier le rôle de l'élément magnétique et le couplage d'interaction magnétique associé, il pourrait être utile d'utiliser avec précision les propriétés de la magnéto sur l'application associée.

Dans ce travail, nous avons étudié les propriétés magnétiques d'un monocristal d'isolant topologique Sb\(_{2}\)Te\(_{3}\) dopé Ni. Une boucle d'hystérésis avec un faible champ coercitif a été observée en dessous de la température de Néel (\(T_{\mathrm {N}}\)). La susceptibilité magnétique révèle un coup de pied à \(T_{\mathrm {N}}\) indépendant du champ magnétique externe. La susceptibilité magnétique des processus froids à champ nul et froid coïncident au-dessus de \(T_{\mathrm {N}}\), et ils sont bifurqués en dessous de \(T_{\mathrm {N}}\). La division de susceptibilité magnétique est plus importante à des températures et des champs magnétiques externes plus faibles. Plus aucune division de susceptibilité magnétique n'est observée à un champ magnétique supérieur à 7000 Oe. Notre étude soutient que ces caractéristiques de susceptibilité magnétique proviennent d'un ordre antiferromagnétique accompagné d'un ferromagnétisme faible. La susceptibilité saturée extraite va bien avec la tendance de la cuspide de susceptibilité magnétique mesurée. Mis à part la plupart des rapports selon lesquels la cuspide de susceptibilité magnétique provient de la texture du spin du porteur au point de Dirac de l'état de surface topologique, nos résultats révèlent qu'elle pourrait être liée au ferromagnétisme des éléments magnétiques.

Méthode expérimentale

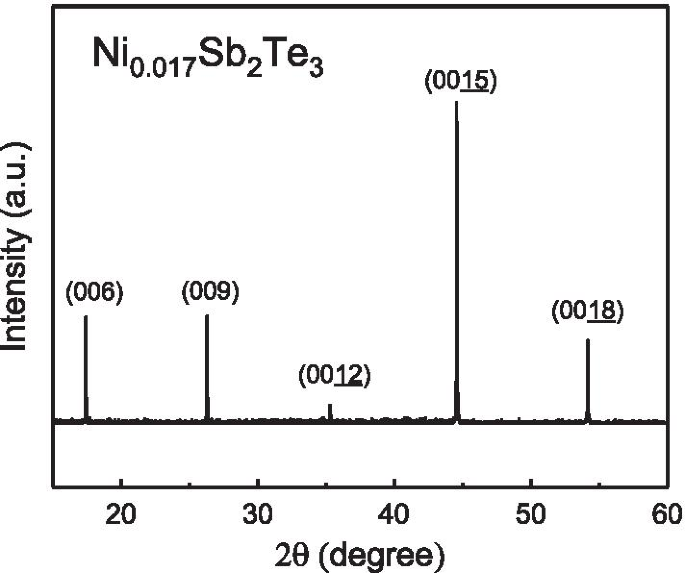
Le spectre XRD du monocristal Ni\(_{0.016}\)Sb\(_{2}\)Te\(_{3}\). Il révèle des pics nets et qui supporte la structure hautement monocristallisée

Des monocristaux de Sb\(_{2}\)Te\(_{3}\) ont été cultivés avec un four à zone flottante chauffé par résistance (RHFZ) fait maison. Les matières premières de départ Sb\(_{2}\)Te\(_{3}\) ont été mélangées selon le rapport stoechiométrique. Dans un premier temps, les mélanges stoechiométriques d'éléments de haute pureté Ni (99,995%), Sb (99,995%) et Te (99,995%) ont été fondus à \(700 \sim 800 ^{\circ }\)C pendant 20 h puis lentement refroidi à température ambiante dans un tube en verre de quartz sous vide. Le matériau a été utilisé comme tige d'alimentation pour l'expérience RHFZ suivante. Nos travaux antérieurs soutiennent qu'une uniformité cristalline extrêmement élevée dans les cristaux isolants topologiques peut être obtenue par la méthode RHFZ. Après croissance, les cristaux ont ensuite été refroidis au four à température ambiante. Les cristaux au fur et à mesure de leur croissance ont été clivés le long du plan basal, avec une surface argentée brillante semblable à un miroir, puis préparés pour d'autres expériences. Les résultats du spectre à dispersion d'énergie (EDS) soutiennent que le \(\mathrm {Ni} :\mathrm {Sb} :\mathrm {Te} =0,017 :2 :3\). La figure 1 montre le spectre de diffraction des rayons X (XRD). Il révèle des pics nets et ces pics sont cohérents avec la base de données de Sb\(_{2}\)Te\(_{3}\). Ceci confirme que notre échantillon est fortement cristallisé. Les atomes de Ni devraient être répartis de manière uniforme et aléatoire dans le monocristal. La taille du cristal est de 3 mm de long, 2 mm de large et 0,42 mm d'épaisseur. Les mesures du magnétisme ont été effectuées en utilisant la technique standard dans un appareil commercial (Quantum Design MPMS) avec un champ magnétique allant jusqu'à 7 T. Le champ magnétique a été appliqué perpendiculairement à la grande surface clivée.

Résultats et discussion

La figure 2 montre la magnétisation en fonction des champs magnétiques à différentes températures, et elle a révélé la caractéristique diamagnétique à une large gamme de champs magnétiques et de températures. Ce diamagnétisme provient du spin du porteur et il est cohérent avec les rapports précédents dans les isolants topologiques BSTS [31]. Comme le montre l'encadré en haut à droite, différent des rapports précédents, une boucle d'hystérésis a été observée à des températures inférieures à 125 K. Le champ coercitif de la boucle d'hystérésis montre une faible dépendance à la température et est d'environ 50 Oe. L'aimantation rémanente et saturée de la boucle d'hystérésis est d'environ \(10^{-5}\) emu/g et \(10^{-4}\) emu/g à 100 K. Le champ coercitif faible, le petit rémanent , et la faible magnétisation saturée indiquent un ferromagnétisme faible. Comme le montre l'encart en bas à gauche, aucune boucle d'hystérésis claire n'a été observée à des températures supérieures à 125 K. Le ferromagnétisme provient des moments magnétiques alignés des éléments magnétiques. L'énergie thermique pourrait rendre aléatoire le moment magnétique aligné et étaler le ferromagnétisme au-dessus d'une température critique. Notre observation indique que le système révèle une transition de ferromagnétisme faible autour de 120 K.

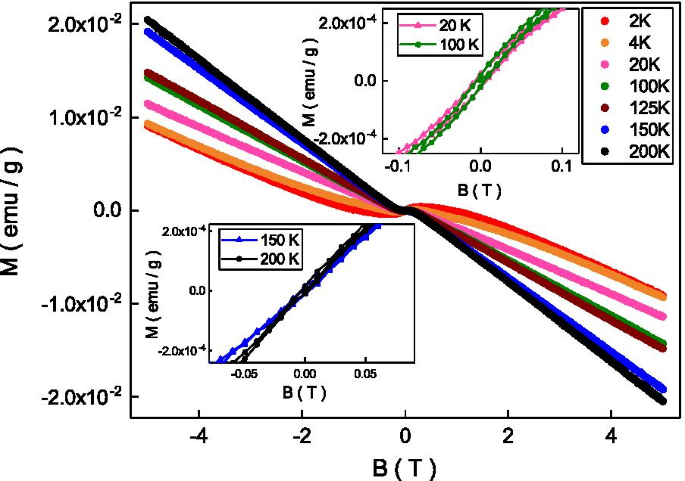
La susceptibilité en fonction des champs magnétiques de 2 à 200 K. Elle révèle le diamagnétisme aux champs magnétiques élevés. Encart en haut à droite :La boucle d'hystérésis a été observée à une température inférieure à 125 K. Encart en bas à gauche :Aucune boucle d'hystérésis n'a été observée à une température supérieure à 125 K

Pour étudier le magnétisme intrinsèque caractéristique de la transition ferromagnétique faible observée, la susceptibilité magnétique dépendante de la température a été réalisée par des processus refroidis par champ et par champ nul. La figure 3 montre la susceptibilité magnétique des processus refroidis par champ et à champ nul à différents champs magnétiques externes. La susceptibilité magnétique augmente lorsque la température diminue. Il révèle une discontinuité à 125 K (\(T_{\mathrm {N}}\)) et le \(T_{\mathrm {N}}\) est indépendant des champs magnétiques externes. Le \(T_{\mathrm {N}}\) est la température de Néel et le mécanisme détaillé sera discuté et clarifié ci-dessous. La susceptibilité magnétique des refroidis par champ et par champ nul coïncide au-dessus de \(T_{\mathrm {N}}\) et bifurque en dessous de \(T_{\mathrm {N}}\). Une division de susceptibilité magnétique plus importante est observée à des champs magnétiques externes plus faibles. Notre résultat expérimental montre que cette discontinuité et le clivage de susceptibilité magnétique n'est plus observé à un champ magnétique supérieur à 7000 Oe. Il est intéressant de noter que la fluctuation du signal au champ magnétique de 50 Oe est évidemment plus grande que les autres champs magnétiques. L'une des raisons possibles est que l'alignement du moment magnétique est métastable à 50 Oe qui est proche du champ coercitif de la boucle d'hystérésis. Comme le montre la figure 2, la boucle d'hystérésis n'a été observée qu'en dessous de 125 K, ce qui correspond à la température critique de la bifurcation de la susceptibilité magnétique de la figure 3. Cela indique que la division de la susceptibilité magnétique observée pourrait être liée au faible ferromagnétique sous le \(T_{\mathrm {N}}\). On sait que l'effet ferromagnétique serait masqué par l'énergie thermique et la susceptibilité magnétique au-dessus de la température critique pourrait être décrite par la loi de Curie-Weiss, \(\chi =\chi _{0} + \frac{C}{ T-\theta }\), où \(\chi\) est la susceptibilité magnétique mesurée, \(\chi _{0}\) est la susceptibilité magnétique à 0 K, C est la constante de Curie qui correspond au magnéton de Bohr, T est la température, et \(\theta\) est la température de Curie [32]. L'encart de la figure 4 montre la dépendance de la température de \(\frac{1}{\chi - \chi _{0}}\) refroidi à champ nul à différents champs magnétiques externes. Le \(\frac{1}{\chi -\chi _{0}}\) est proportionnel à une température comprise entre 125 et 250 K, et la pente est plus importante à des champs magnétiques externes plus faibles. La pente est liée à la constante de Curie. L'extrapolation linéaire du \(\frac{1}{\chi -\chi _{0}}\) entre 125 et 250 K de tous les champs magnétiques externes coïncide à -125 K. Suivant la loi de Curie-Weiss, cette valeur correspond au \(\theta\). Le négatif \(\theta\) (-125 K) indique qu'il s'agit d'un système antiferromagnétique en dessous du \(T_{\mathrm {N}}\) et \(T_{\mathrm {N}}\) est appelé Température de Néel [33]. La valeur absolue du \(\theta\) est cohérente avec le \(T_{\mathrm {N}}\) observé sur la figure 3 , et la température critique pour observer la boucle d'hystérésis (125 K) sur la figure 2 Ces observations indiquent que ferromagnétisme faible et antiferromagnétisme coexistent en dessous de \(T_{\mathrm {N}}\).

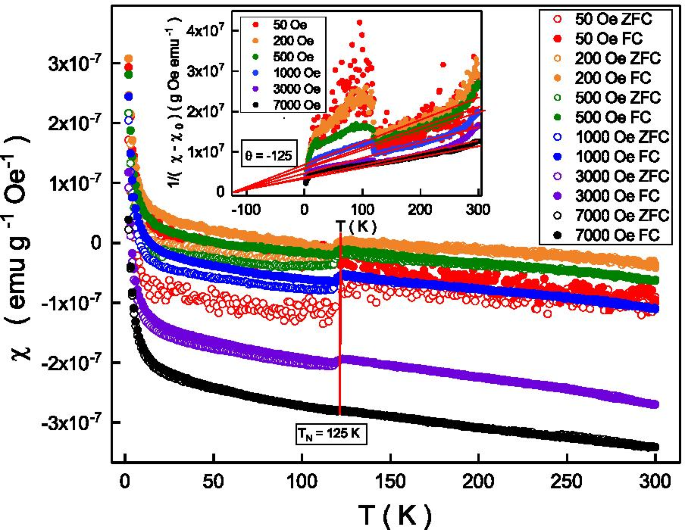
La susceptibilité magnétique des processus refroidis par champ et à champ nul à différents champs magnétiques externes. La susceptibilité magnétique des refroidis par champ et par champ nul coïncide au-dessus de 125 K et bifurque en dessous de 125 K. Une plus grande susceptibilité magnétique se divise à des champs magnétiques externes et à des températures plus faibles. Plus aucune division de susceptibilité magnétique n'est observée à un champ magnétique supérieur à 7000 Oe. Encart en haut à droite :la susceptibilité magnétique suit la loi de Curie-Weiss

Comme le montre l'encadré de la figure 3, la constante de Curie, C , est plus grand à des champs magnétiques plus élevés. Suivant la fonction paramagnétique de Langevin, C pourrait être exprimé comme \(C=\frac{N\mu _{0}\mu ^{2}}{3k_{\mathrm {B}}T}\) où N est le nombre d'éléments magnétiques par unité de gramme, \(\mu\) est le moment effectif d'un élément magnétique, \(\mu _{0}\) est la perméabilité au vide et \(k_{\mathrm {B}} \) est la constante de Boltzmann [34]. Le \(\mu\) estimé à 200 Oe est d'environ 3,5 \(\mu _{\mathrm {B}}\) ce qui est proche de la valeur théorique de 3,32 \(\mu _{\mathrm {B}}\ ) [35]. Cela confirme que le comportement du magnétisme pourrait être expliqué par la loi de Curie-Weiss.

Le moment magnétique est gelé au hasard dans le champ zéro froid et gelé le long de la direction du champ magnétique externe dans le champ froid. La bifurcation de susceptibilité magnétique provient de l'anisotropie magnétique. Cette caractéristique pourrait être une caractéristique d'un ordre antiferromagnétique accompagné d'un ferromagnétisme faible; Les moments ferromagnétiques des domaines gèlent dans une direction aléatoire en champ zéro-froid, alors qu'ils sont forcés de s'aligner le long du champ magnétique appliqué lors du refroidissement à travers \(T_{\mathrm {N}}\) en champ froid [36]. Comme discuté ci-dessus, il se compose à la fois de caractéristiques ferromagnétiques et antiferromagnétiques faibles en dessous de \(T_{\mathrm {N}}\) dans notre système. Le faible alignement ferromagnétique briserait légèrement l'ordre antiferromagnétique et induirait l'anisotropie magnétique. La bifurcation de susceptibilité magnétique pourrait être comprise comme un ferromagnétisme faible dans un système antiferromagnétique. Ces résultats confirment que la bifurcation de susceptibilité magnétique observée en dessous de 125 K est la caractéristique magnétique du ferromagnétisme faible dans un système antiferromagnétique. La division de susceptibilité différente à différents champs magnétiques externes pourrait provenir du niveau de polarisation partielle différent de l'antiferromagnétisme aux champs magnétiques externes.

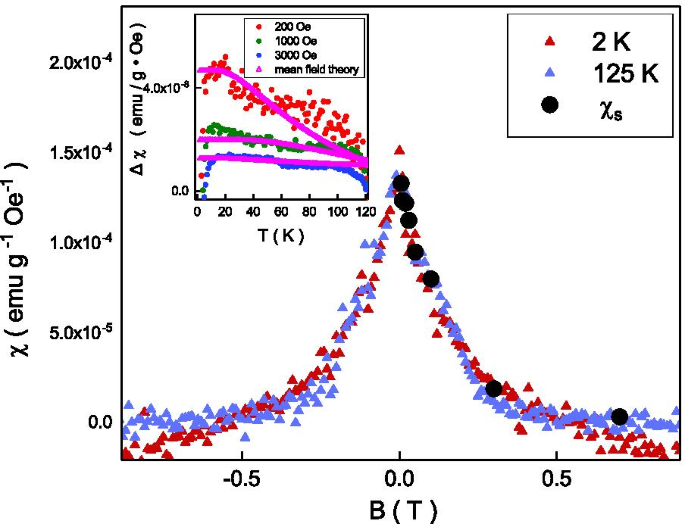
Encart en haut à gauche :la différence de susceptibilité magnétique entre le refroidissement par champ et le refroidissement par champ nul suit la théorie du champ moyen. La susceptibilité saturée extraite va bien avec la tendance de la cuspide de susceptibilité magnétique mesurée

Suivant la théorie du champ moyen, [37] le \(T_{\mathrm {N}}\) est lié à la force de couplage d'échange, \(J_{0}\), et il pourrait être exprimé comme \(T_{\ mathrm {N}}=\frac{S(S+1)}{3k_{\mathrm {B}}T}J_{0}\), où S est le moment de spin, \(k_{\mathrm {B}}\) est la constante de Boltzmann. Le \(J_{0}\) irait à \(4,28 \times 10^{22}\) joule dans notre système avec \(T_{\mathrm {N}}\) =125 K. La théorie du champ moyen prend en charge que l'aimantation est liée à l'énergie thermique par un facteur de \(e^{\frac{-J_{0}S}{k_{\mathrm {B}}T}}\). La susceptibilité magnétique pourrait être exprimée sous la forme \(\chi =\chi _{\mathrm {S}}(1-e^{\frac{-J_{0}S}{k_{\mathrm {B}}T}} )\), où \(\chi _{\mathrm {S}}\) est la susceptibilité magnétique saturée. La division de susceptibilité magnétique, \(\chi _{\mathrm {FC}}-\chi _{\mathrm {ZFC}}\) pourrait être exprimée comme \(\chi _{\mathrm {S}}e^{\ frac{-J_{0}S}{k_{\mathrm {B}}T}}\). Le \(\chi _{\mathrm {S}}\) est sensible aux champs magnétiques externes. Comme le montre l'encadré de la figure 4, cette équation pourrait bien expliquer notre résultat expérimental dans une large gamme de températures et de champs magnétiques externes. Le \(\chi _{\mathrm {S}}\) extrait est fonction des champs magnétiques externes. Pour examiner plus en détail le résultat, la susceptibilité dépendante du champ magnétique est effectuée à des températures inférieures à \(T_{\mathrm {N}}\), et elle montre une cuspide à des champs magnétiques nuls. Cette cuspide de susceptibilité magnétique à champ magnétique nul est largement observée dans les matériaux topologiques, et on suppose qu'elle provient de la texture de spin libre au point de Dirac [38]. La spectroscopie de photoémission à résolution angulaire (ARPES) révèle que le niveau de Fermi se situe en dessous du point de Dirac dans notre Sb\(_{2}\)Te\(_{3}\) [39]. La cuspide observée ne doit pas provenir de la texture de spin au point de Dirac. D'autre part, le champ coercitif de la boucle d'hystérésis est d'environ 50 Oe, soit deux ordres de grandeur inférieur à la pleine largeur à mi-hauteur de la cuspide, 0,4 T, et la boucle d'hystérésis ne doit pas être la source principale de la cuspide observée. . Comme le montre l'encart de la figure 4, le \(\chi _{\mathrm {S}}\) dépendant du champ magnétique extrait suit la même tendance de champ magnétique de la susceptibilité magnétique mesurée. Cela indique que la cuspide de susceptibilité largement observée pourrait provenir de l'ordre antiferromagnétique accompagné d'un faible alignement de ferromagnétisme.

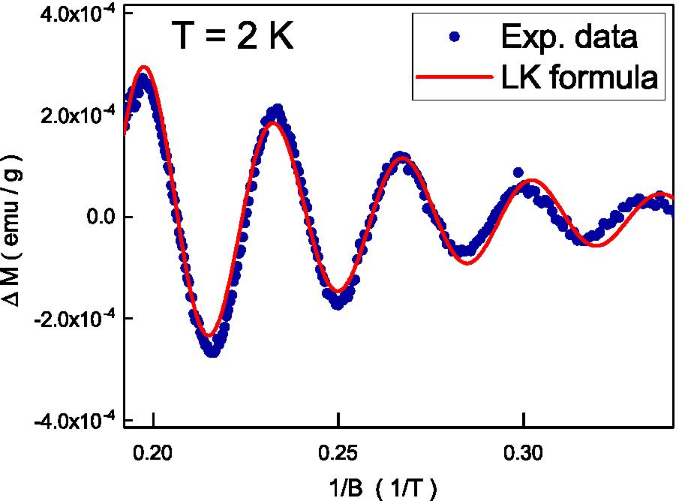
Les oscillations dHvA en fonction des champs magnétiques inverses. Le résultat expérimental correspond bien à l'équation théorique

Suite à l'analyse, la bifurcation de susceptibilité provient du magnétisme d'ordre ferromagnétique faible accompagné d'antiferromagnétisme. Le dédoublement de susceptibilité magnétique est lié à l'anisotropie magnétocristalline. Ici, nous estimons davantage l'énergie d'anisotropie magnétocristalline, \(\Delta E =\frac{M_{\mathrm {S}}H_{\mathrm {C}}V}{2}\), où \(H_{\mathrm {C}}=50\) Oe, \(M_{\mathrm {S}}=1.81\times 10^{-11}\) J/T et \(V=2.5\times 10^{-9}\ ) m\(^{3}\) dans notre système, et le \(\Delta E \sim 1.13 \times 10^{22}\) Joule [40]. En suivant l'énergie du moment magnétique, \(g\mu _{\mathrm {B}}B\), on pourrait estimer que l'énergie d'anisotropie magnétocristalline sera inférieure à l'énergie du moment magnétique à \(B> 0,61\) T. Cela est cohérent avec notre observation selon laquelle la division de la susceptibilité magnétique n'est plus observée à des champs magnétiques externes supérieurs à 0,7 T.

La figure 5 montre la susceptibilité magnétique en fonction de 1/B et il montre des oscillations périodiques. Ceci est connu sous le nom d'oscillations à effet De Haas-Van Alphen (dHvA) qui proviennent du mouvement orbital d'électrons itinérants à des champs magnétiques élevés [41]. Nous analysons les oscillations dHvA en adaptant l'aimantation oscillatoire à la formule de Lifshitz-Kosevich (LK) [42], \(\Delta M \propto -R \sin [2\pi (\frac{F}{B}-\delta _{p})]\). R est liée au taux de diffusion des porteurs, à l'effet Zeeman et à l'élargissement du niveau de Landau [43]. L'oscillation est décrite par un terme sinusoïdal qui contient le facteur de phase \(\delta _{p}\). \(\delta _{p}\) est lié à la phase Berry (\(\Phi _{B}\)), \(\delta _{p} =\frac{1}{2}-\frac{ \Phi _{B}}{2\pi }\). La dimension de la poche de Fermi caractérise la valeur \(\delta _{p}\). Comme le montre la Fig. 5, l'équation théorique correspond bien à notre résultat expérimental et les extraits \(\delta _{p}=0.43\) et \(F =29.8\) T. Cela est cohérent avec la prédiction théorique et le La dHvA observée provient de l'état de surface topologique. En suivant la relation d'Onsager [44], \(F=\frac{\hbar K_F^{2}}{2\pi }\), on pourrait estimer que \(K_{F} =0,030\)Å ^{− 1} est cohérent avec la valeur rapportée de l'ARPES. Ces résultats suggèrent que les oscillations dHvA proviennent de l'état de surface topologique.

Conclusion

Dans ce travail, nous avons étudié le comportement magnétique d'un monocristal d'isolant topologique Sb\(_{2}\)Te\(_{3}\) dopé Ni. Une boucle d'hystérésis avec un faible champ coercitif a été observée en dessous de la température de Néel. La susceptibilité magnétique révèle un coup de pied à température de Nèel indépendant du champ magnétique extérieur. La susceptibilité magnétique des processus de refroidissement à champ nul et de refroidissement à champ coïncident au-dessus de la température de Néel et il y a une bifurcation au-dessous de la température de Néel. La division de susceptibilité magnétique est plus grande à un champ magnétique externe inférieur. On n'observe plus de dédoublement de susceptibilité magnétique lorsque l'énergie d'anisotropie du moment magnétique est inférieure à l'énergie du moment magnétique à 0,7 T. Notre étude soutient que ces caractéristiques de susceptibilité magnétique proviennent d'un ordre antiferromagnétique accompagné d'un ferromagnétisme faible. La susceptibilité magnétique saturée extraite va bien avec la tendance de la cuspide de susceptibilité magnétique mesurée. Cela indique que la cuspide de susceptibilité largement observée pourrait provenir du faible ferromagnétisme. L'oscillation dHvA est cohérente avec la prédiction théorique. Cela confirme que l'oscillation dHvA observée provient de l'état de surface topologique.

Disponibilité des données et des matériaux

Les ensembles de données générés et/ou analysés au cours de la présente étude sont disponibles auprès des auteurs correspondants sur demande raisonnable.

Abréviations

XPD :

Diffraction des rayons X

EDS :

Spectroscopie à rayons X à dispersion d'énergie

ARPES :

Spectroscopie de photoémission résolue en angle

dHvA :

De Haas-Van Alphen