Résoudre des équations simultanées :la méthode de substitution et la méthode d'addition

Que sont les équations simultanées et les systèmes d'équations ?

Les termes équations simultanées et systèmes d'équations font référence à des conditions dans lesquelles deux ou plusieurs variables inconnues sont liées les unes aux autres par un nombre égal d'équations.

Exemple :

Pour cet ensemble d'équations, il n'y a qu'une seule combinaison de valeurs pour x et y qui satisfera les deux.

L'une ou l'autre équation, considérée séparément, a une infinité de (x,y) valides solutions, mais ensemble il n'y a qu'un seul. Tracée sur un graphique, cette condition devient évidente :

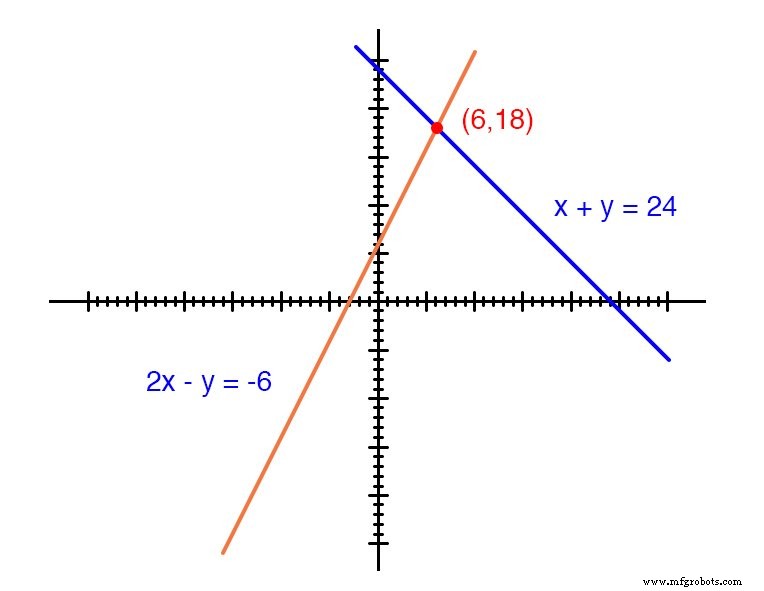
Chaque ligne est en fait un continuum de points représentant les x possibles et y paires de solutions pour chaque équation.

Chaque équation, séparément, a un nombre infini de paires ordonnées (x ,y ) solutions. Il n'y a qu'un seul point où les deux fonctions linéaires x + y =24 et 2x - y =-6 se croisent (où l'une de leurs nombreuses solutions indépendantes fonctionne pour les deux équations), et c'est là que x est égal à une valeur de 6 et y est égal à une valeur de 18.

Habituellement, cependant, la représentation graphique n'est pas un moyen très efficace de déterminer l'ensemble de solutions simultanées pour deux ou plusieurs équations. C'est particulièrement peu pratique pour les systèmes de trois variables ou plus.

Dans un système à trois variables, par exemple, la solution serait trouvée par l'intersection ponctuelle de trois plans dans un espace de coordonnées tridimensionnel, ce qui n'est pas un scénario facile à visualiser.

Résoudre des équations simultanées à l'aide de la méthode de substitution

Plusieurs techniques algébriques existent pour résoudre des équations simultanées.

Le plus simple à comprendre est peut-être la substitution méthode.

Prenons, par exemple, notre exemple de problème à deux variables :

Dans la méthode de substitution, nous manipulons l'une des équations de telle sorte qu'une variable soit définie en fonction de l'autre :

Ensuite, nous prenons cette nouvelle définition d'une variable et substitut pour la même variable dans l'autre équation.

Dans ce cas, on prend la définition de y , qui est 24 - x et remplacez ceci par le y terme trouvé dans l'autre équation :

Maintenant que nous avons une équation avec une seule variable (x ), on peut le résoudre en utilisant des techniques algébriques « normales » :

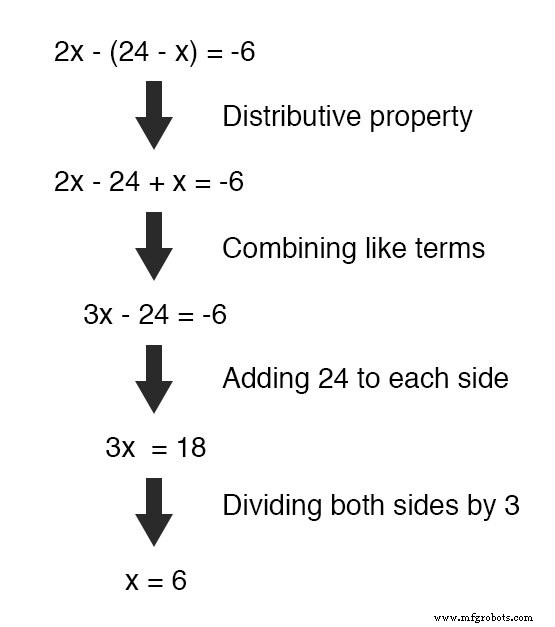
Maintenant que x est connue, nous pouvons insérer cette valeur dans n'importe laquelle des équations d'origine et obtenir une valeur pour y.

Ou, pour nous épargner du travail, nous pouvons brancher cette valeur (6) dans l'équation que nous venons de générer pour définir y en termes de x , étant qu'il est déjà sous une forme à résoudre pour y :

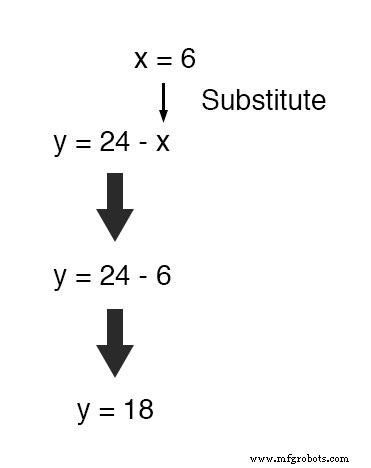
L'application de la méthode de substitution à des systèmes de trois variables ou plus implique un modèle similaire, mais avec plus de travail impliqué.

Ceci est généralement vrai pour n'importe quelle méthode de solution :le nombre d'étapes nécessaires pour obtenir des solutions augmente rapidement avec chaque variable supplémentaire dans le système.

Pour résoudre trois variables inconnues, nous avons besoin d'au moins trois équations. Considérez cet exemple :

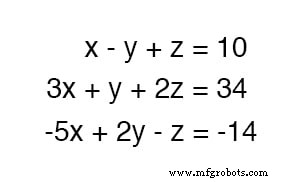
Étant donné que la première équation a les coefficients les plus simples (1, -1 et 1, pour x , y , et z , respectivement), il semble logique de l'utiliser pour développer une définition d'une variable en fonction des deux autres.

Résoudre pour x en termes de y et z :

Maintenant, nous pouvons substituer cette définition de x où x apparaît dans les deux autres équations :

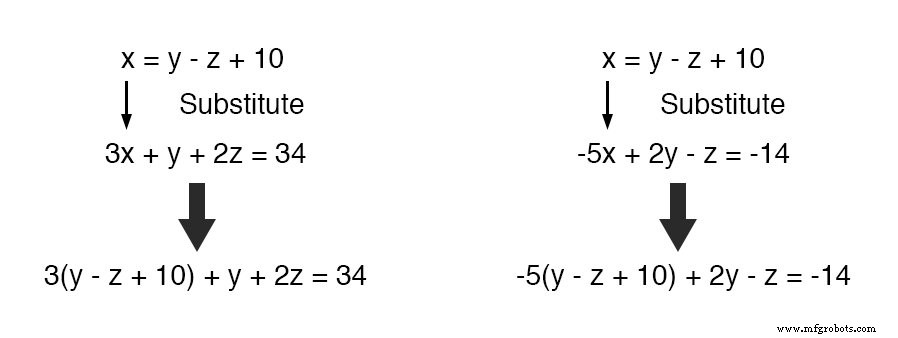
En réduisant ces deux équations à leurs formes les plus simples :

Jusqu'à présent, nos efforts ont réduit le système de trois variables dans trois équations à deux variables dans deux équations.

Maintenant, nous pouvons appliquer à nouveau la technique de substitution aux deux équations 4y - z =4 et -3y + 4z =36 à résoudre pour y ou z . Tout d'abord, je vais manipuler la première équation pour définir z en termes de y :

Ensuite, nous allons substituer cette définition de z en termes de y où l'on voit z dans l'autre équation :

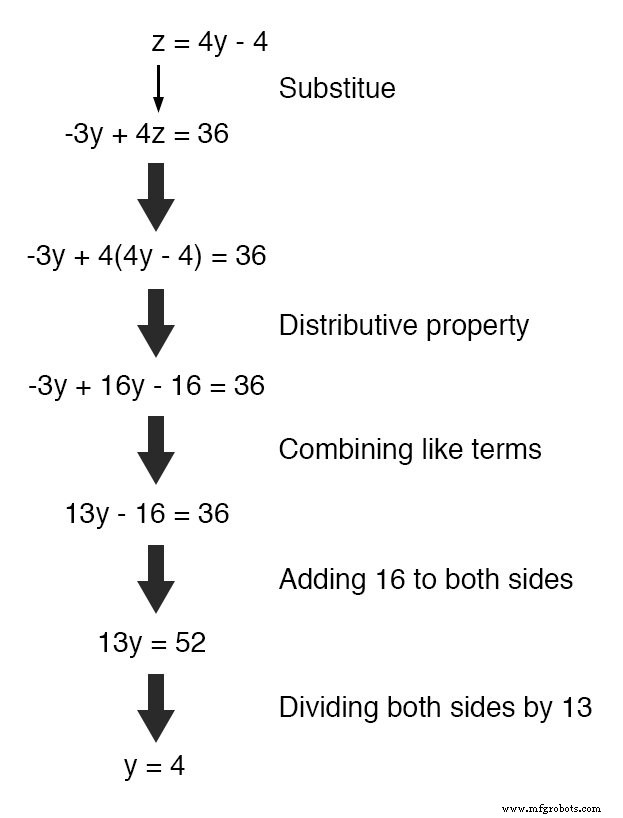
Maintenant que y est une valeur connue, nous pouvons la brancher dans l'équation définissant z en termes de y et obtenez un chiffre pour z :

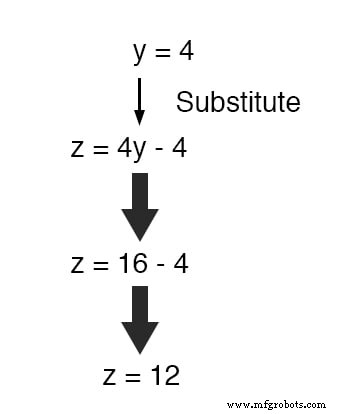
Maintenant, avec des valeurs pour y et z connus, nous pouvons les intégrer dans l'équation où nous avons défini x en termes de y et z , pour obtenir une valeur pour x :

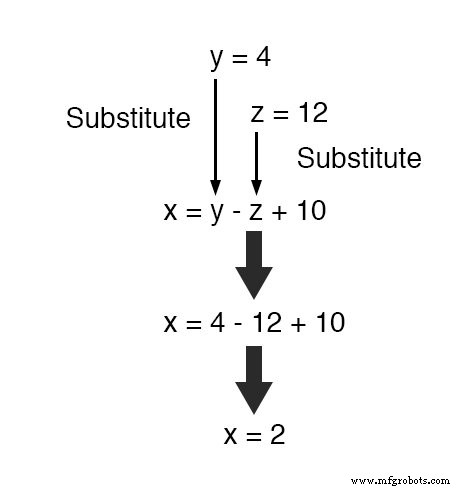
En terminant, nous avons trouvé des valeurs pour x , y , et z de 2, 4 et 12, respectivement, qui satisfont les trois équations.

Résolution d'équations simultanées à l'aide de la méthode d'addition

Alors que la méthode de substitution est peut-être la plus facile à appréhender sur le plan conceptuel, il existe d'autres méthodes de solution à notre disposition.

L'une de ces méthodes est la soi-disant addition méthode, dans laquelle les équations sont additionnées les unes aux autres dans le but d'annuler les termes variables.

Prenons notre système à deux variables utilisé pour démontrer la méthode de substitution :

L'une des règles les plus utilisées de l'algèbre est que vous pouvez effectuer n'importe quelle opération arithmétique que vous souhaitez sur une équation tant que vous le faites également des deux côtés .

En ce qui concerne l'addition, cela signifie que nous pouvons ajouter n'importe quelle quantité que nous souhaitons des deux côtés d'une équation, tant qu'elle est la même quantité—sans altérer la vérité de l'équation.

Une option que nous avons, alors, est d'ajouter les côtés correspondants des équations ensemble pour former une nouvelle équation.

Puisque chaque équation est une expression d'égalité (la même quantité de chaque côté du = signe), ajouter le côté gauche d'une équation au côté gauche de l'autre équation est valide tant que nous additionnons également les côtés droit des deux équations.

Dans notre exemple d'ensemble d'équations, par exemple, nous pouvons ajouter x + y à 2x - y , et ajoutez 24 et -6 ensemble pour former une nouvelle équation.

Quel avantage cela nous apporte-t-il ? Examinez ce qui se passe lorsque nous faisons cela à notre exemple d'ensemble d'équations :

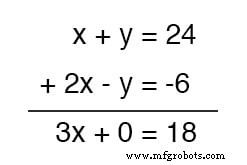
Parce que l'équation du haut contenait un y positif terme alors que l'équation du bas contenait un y négatif terme, ces deux termes se sont annulés dans le processus d'addition, ne laissant aucun y terme dans la somme.

Ce qui nous reste est une nouvelle équation, mais avec une seule variable inconnue, x ! Cela nous permet de résoudre facilement la valeur de x :

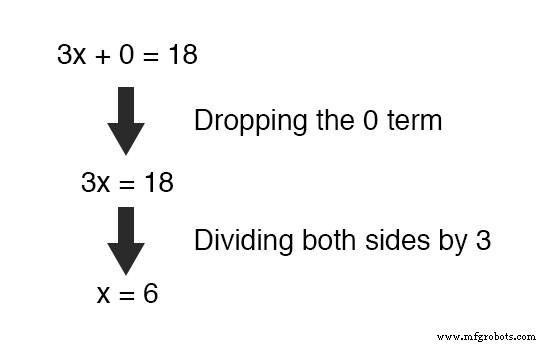
Une fois que nous avons une valeur connue pour x , bien sûr, en déterminant y La valeur de est une simple question de substitution (en remplacement de x avec le nombre 6 ) dans l'une des équations originales.

Dans cet exemple, la technique consistant à additionner les équations a bien fonctionné pour produire une équation avec une seule variable inconnue.

Qu'en est-il d'un exemple où les choses ne sont pas si simples ? Considérons l'ensemble d'équations suivant :

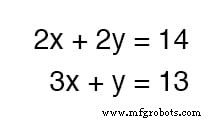
Nous pourrions additionner ces deux équations - ceci étant une opération algébrique tout à fait valide - mais cela ne nous profiterait pas dans le but d'obtenir des valeurs pour x et y :

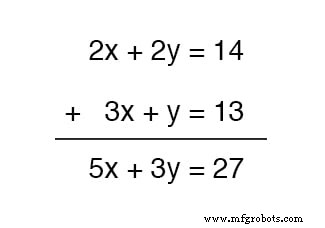
L'équation résultante contient toujours deux variables inconnues, tout comme les équations d'origine, et nous ne sommes donc pas plus avancés dans l'obtention d'une solution.

Cependant, et si nous pouvions manipuler l'une des équations de manière à avoir un terme négatif qui aurait annuler le terme respectif dans l'autre équation lorsqu'il est ajouté ?

Ensuite, le système se réduirait à une seule équation avec une seule variable inconnue comme dans le dernier exemple (fortuit).

Si seulement nous pouvions tourner le y terme dans l'équation inférieure dans un - 2y terme, de sorte que lorsque les deux équations ont été additionnées, les deux y les termes des équations s'annuleraient, ne nous laissant qu'un x terme, cela nous rapprocherait d'une solution.

Heureusement, ce n'est pas difficile à faire. Si nous multiplions chaque terme de l'équation inférieure par un -2 , il produira le résultat recherché :

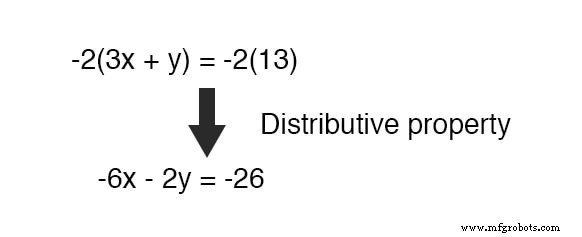
Maintenant, nous pouvons ajouter cette nouvelle équation à l'équation supérieure d'origine :

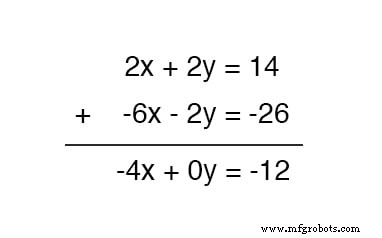
Résolution de x , on obtient une valeur de 3 :

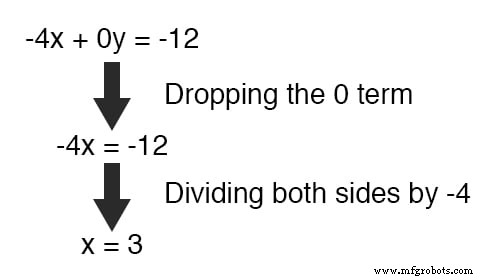
Substitution de cette nouvelle valeur à x dans l'une des équations d'origine, la valeur de y est facile à déterminer :

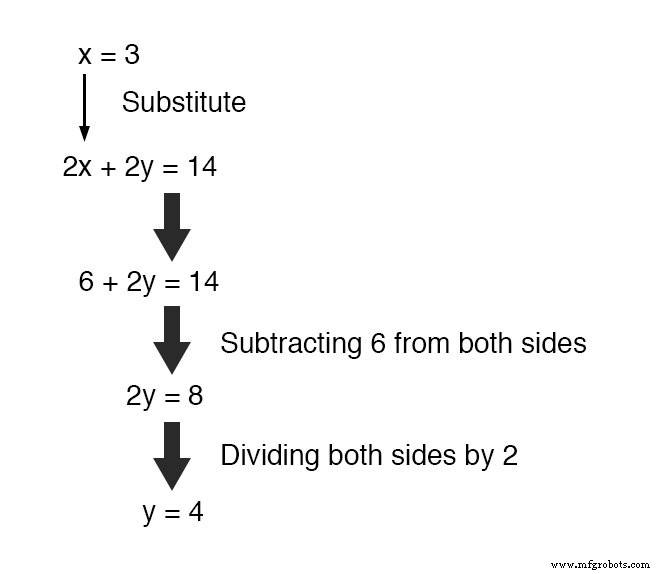
L'utilisation de cette technique de résolution sur un système à trois variables est un peu plus complexe.

Comme pour la substitution, vous devez utiliser cette technique pour réduire le système à trois équations de trois variables à deux équations à deux variables, puis l'appliquer à nouveau pour obtenir une seule équation avec une variable inconnue.

Pour le démontrer, j'utiliserai le système d'équations à trois variables de la section substitution :

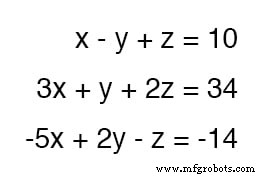
Étant donné que l'équation du haut a des valeurs de coefficient de 1 pour chaque variable, ce sera une équation facile à manipuler et à utiliser comme outil d'annulation.

Par exemple, si nous souhaitons annuler le 3x terme de l'équation du milieu, il suffit de prendre l'équation du haut, de multiplier chacun de ses termes par -3 , puis ajoutez-le à l'équation du milieu comme ceci :

Nous pouvons débarrasser l'équation du bas de ses -5x terme de la même manière :prenez l'équation du haut d'origine, multipliez chacun de ses termes par 5 , puis ajoutez cette équation modifiée à l'équation du bas, en laissant une nouvelle équation avec seulement y et z termes :

À ce stade, nous avons deux équations avec les deux mêmes variables inconnues, y et z :

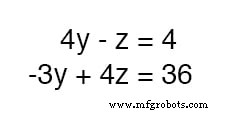
Par inspection, il devrait être évident que le -z terme de l'équation supérieure pourrait être utilisé pour annuler le 4z terme dans l'équation inférieure si seulement nous multiplions chaque terme de l'équation supérieure par 4 et additionnez les deux équations :

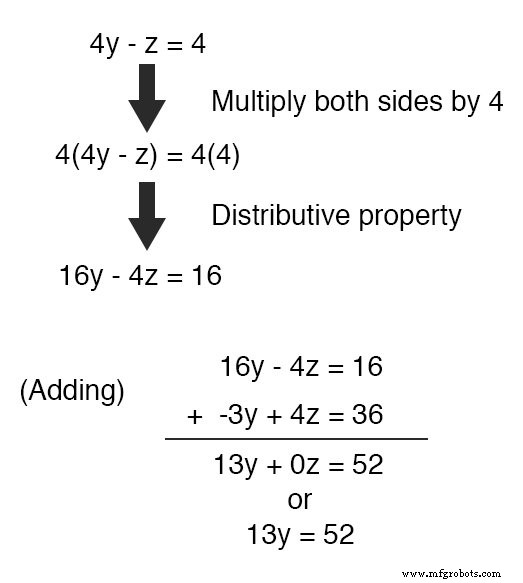
Prenant la nouvelle équation 13y =52 et résoudre pour y (en divisant les deux côtés par 13 ), on obtient une valeur de 4 pour y .

Substituer cette valeur de 4 pour y dans l'une ou l'autre des équations à deux variables nous permet de résoudre pour z .

Substitution des deux valeurs de y et z dans l'une des équations originales à trois variables nous permet de résoudre pour x .

Le résultat final (je vous épargne les étapes algébriques puisque vous devriez les connaître maintenant !) est que x =2 , y =4 , et z =12 .

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail sur les équations simultanées pour l'analyse de circuits