Absorptivité élevée des photons des photodétecteurs infrarouges à points quantiques obtenue grâce à l'effet plasmon de surface d'un réseau de nanotrous métalliques

Contexte

Les photodétecteurs infrarouges à semi-conducteurs peuvent être utilisés pour détecter la lumière infrarouge et ont de grandes applications prometteuses dans les domaines de la recherche scientifique, de l'imagerie numérique, de la communication optique et des domaines militaires. À ce jour, les photodétecteurs infrarouges à points quantiques (QDIP) ont attiré une attention croissante ces dernières années en raison de leurs propriétés exceptionnelles de réponse lumineuse et de leur tendance à la miniaturisation des dispositifs [1,2,3]. Bien que des décennies d'efforts soutenus aient fait de grands progrès dans le développement de technologies permettant d'obtenir des QDIP hautes performances, des améliorations supplémentaires doivent encore être apportées pour relever les défis de la miniaturisation des appareils [4] et des exigences pratiques. Il est souligné que le couplage de réseaux métalliques sur la région active basée sur les points quantiques pourrait être considéré comme une approche efficace pour améliorer les performances des QDIP [5, 6], ce qui peut produire un coefficient de photoabsorption élevé par le photocouplage local de plasmons améliorés. effet.

Selon les rapports, il existe deux principaux types de structures de grilles métalliques utilisées pour améliorer les performances des QDIP. L'une est la structure de réseau de trous métalliques et l'autre est la structure de réseau de métaux sans trous. Plus concrètement, en ce qui concerne l'application de la structure du réseau de trous métalliques, le groupe de Chang a combiné le réseau périodique de trous métalliques avec la couche de points quantiques dans le QDIP en 2007, ce qui a conduit à la transmission de lumière supranormale du photodétecteur [7]. En 2009, Lee et al. ont proposé une méthode de QDIP à haute détectivité en intégrant des cristaux photoniques métalliques avec une période de 3,6 µm de matrice de trous (épaisseur de 100 nm) [8]. Les résultats de la recherche démontrent que la méthode peut atteindre la réponse maximale du photodétecteur à la longueur d'onde de 11,3 µm et produire une détectivité jusqu'à 30 fois supérieure à celle sans cristal photonique métallique. Ensuite, ils ont discuté des performances de la dépendance QDIP vis-à-vis de la lumière incidente et de leur application dans le réseau plan focal [9, 10]. Une amélioration des performances similaire peut également être trouvée dans les rapports en utilisant le réseau de couplage de réseaux de trous métalliques [11,12,13,14]. Des structures de réseau métallique sans trou sont également proposées. En 2011, Huang et ses collègues ont utilisé la couche de nanoparticules d'argent plasmon auto-organisée pour améliorer la large réponse spectrale du QDIP et ont obtenu une amélioration de 2,4 à 3,3 fois [15]. En 2014, le groupe de Chen a signalé que les performances du photodétecteur peuvent être améliorées grâce à l'effet de champ proche des nanoparticules d'Au [16]. En 2015, le groupe de Ding et le groupe de Wang ont proposé respectivement les structures de couplage de guide d'ondes et la cavité résonante unique du réflecteur de Prague distribué [17, 18]. Outre les structures susmentionnées, d'autres structures métalliques, par exemple le réseau de bandes d'antennes et le réseau de nanodisques ont également été discutées et analysées [19,20,21].

Cependant, ces méthodes de réseau sans trous peuvent également présenter un effet amélioré dans la photo-réponse des QDIP, mais son processus de fabrication avec des méthodes simples et rentables reste un défi par rapport à la structure de réseau de trous typique. Pour les structures de réseau de trous typiques, la taille du réseau de trous est commune à l'échelle microscopique. L'amélioration de la photo-réponse se fait par l'effet plasmon à l'interface entre l'air dans les trous métalliques microscopiques et le semi-conducteur en dessous. La taille du réseau de trous métalliques peut être encore réduite pour correspondre à l'échelle nanométrique attendue à la taille du point quantique dans le QDIP nanométrique, que les QDIP hautes performances avec effet d'amélioration correspondant puissent être réalisés ou non. Parallèlement, d'autres travaux théoriques sont nécessaires pour élucider les mécanismes sous-jacents à ces phénomènes. Dans cette étude, pour rendre le phénomène clair, les QDIP avec les structures de réseau de trous métalliques à l'échelle nanométrique sont conçus, et plus important par rapport aux QDIP microscopiques conventionnels, l'effet d'amélioration est expliqué en analysant la condition de transmission optique et la distribution du champ électrique. . Les résultats démontrent que les QDIP avec les structures de réseau métallique à l'échelle nanométrique peuvent avoir une absorptivité des photons jusqu'à 86,47% en raison de l'interaction photon-point quantique et du couplage efficace de la lumière, ce qui peut ouvrir la porte à la conception et à l'optimisation de l'infrarouge nanométrique. photodétecteur.

Modèle de conception du QDIP avec le Nanohole Array

En général, le QDIP se compose de la région de points quantiques et des électrodes, et la région de points quantiques est composée d'une couche de points quantiques de période et de couches barrières. Dans des conditions idéales (en ignorant les influences des électrodes et du substrat), la transmission optique de l'ensemble du QDIP peut être supposée égale à celle de la région de la boîte quantique. Ainsi, les électrodes et le substrat n'ont pas besoin d'apparaître dans la conception du QDIP. Plus précisément, la figure 1 a donne la conception du QDIP typique, qui est composé de couches composites de points quantiques à 5 périodes, et ces couches composites sont constituées de la couche barrière A1GaAs et des couches GaAs comprenant les points quantiques périodiques (Fig. 1b). Dans la configuration actuelle, les nanoparticules de points quantiques sont supposées avoir la forme d'un cube qui correspond à la définition des points quantiques formés avec de nombreux atomes et molécules, et elle mesure 40 nm de longueur, 40 nm de largeur et 7 ~ 9 nm de hauteur. Un modèle similaire de points quantiques peut également être trouvé dans la littérature rapportée [22]. La zone du QDIP est définie sur 1000 nm × 1000 nm et l'épaisseur des couches barrières AlGaAs est de 60  nm. Le réseau de nanotrous métalliques choisi comme Au est placé sur les couches de nanostructure de points quantiques classiques du QDIP conventionnel, qui est nommé comme le QDIP amélioré affiché sur la figure 2. Le rayon des trous peut être ajusté dans la plage de 50 ~ 70  nm . Il est à noter que le matériau utilisé pour constituer la boîte quantique ne peut pas être simplement considéré comme un matériau massif avec un certain indice de réfraction. La figure 3 révèle la caractéristique de dispersion électrique du matériau GaAs utilisé pour former la boîte quantique en utilisant la méthode d'Edward D. Palik [23]. Sur la figure, la courbe bleue et la courbe rouge représentent la constante diélectrique de GaAs ε ^′ et ε ^″ , respectivement. Les figures 4 a et b montrent la caractéristique de dispersion électrique du GaAs, Al_0,3 Ga_0.7 En tant que matériau et matériau d'or, respectivement.

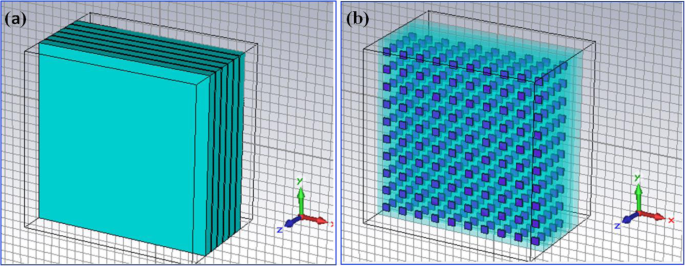
un Diagramme de modèle structurel du photodétecteur infrarouge à points quantiques typique. b Distribution des points quantiques dans les régions actives avec des couches composites de points quantiques à 5 périodes. Ces couches composites sont constituées de la couche barrière A1GaAs et des couches GaAs

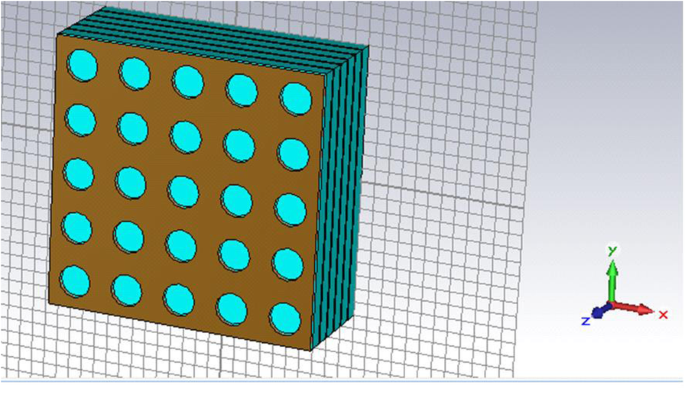
Régions actives de points quantiques avec les structures de réseau de nanotrous métalliques périodiques pour le QDIP amélioré

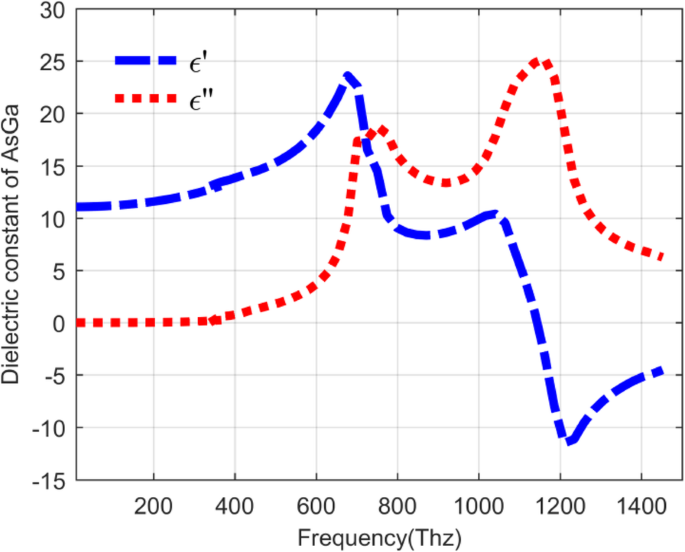
Relation de dispersion du matériau GaAs

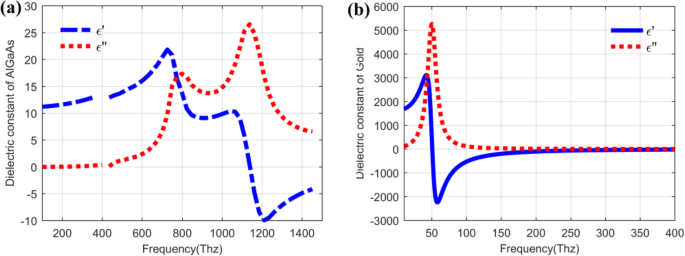
un Relation de dispersion du matériau AlGaAs. b Relation de dispersion du matériau Au

Méthode de calcul basée sur la cellule YEE

Sur la base du modèle physique ci-dessus conçu, la méthode d'intégration par éléments finis est utilisée pour calculer l'état de la transmission optique. Tout d'abord, sur la base des cellules YEE, les équations intégrales de Maxwell satisfaisant le modèle ci-dessus s'écrivent comme suit :

Dans notre calcul, les équations. 1 à 4 sont discrétisés. La distribution des nœuds de champ électrique et les nœuds de champ magnétique sont choisis au format « Cellule Yee ». En utilisant l'éq. 1 à titre d'exemple, le modèle électromagnétique du photodétecteur peut être pris comme l'accumulation de « Yee cell ». Comme le montre la figure 5, les quatre côtés de la cellule arbitraire correspondent à l'équation. 1, représentant le vecteur champ électrique e _i ,e _j ,e _k , et e _l . Le vecteur situé dans la direction normale est le vecteur champ magnétique b _n , et donc l'équation précédente. 1 peut être réécrit comme l'équation suivante. 5.

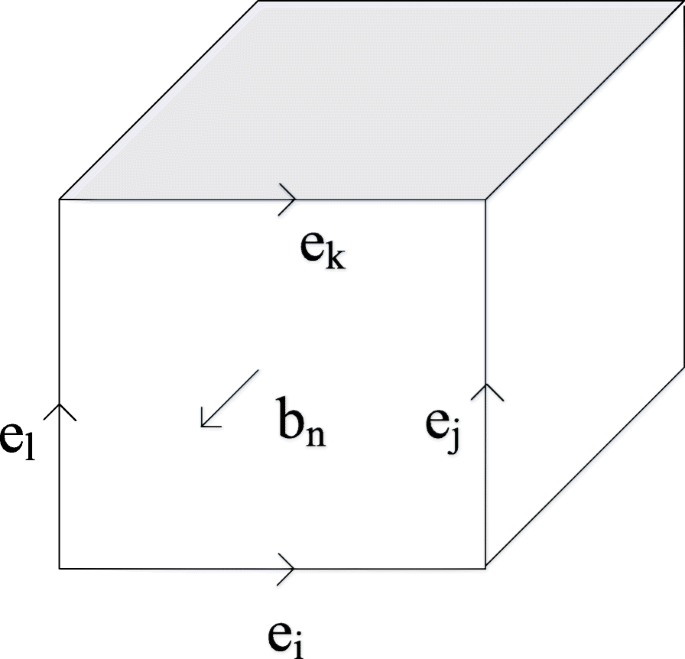
Schéma de principe de la « cellule YEE »

En adoptant une méthode similaire, l'équation du modèle électromagnétique de l'ensemble du photodétecteur peut s'écrire :

L'équation 2 peut également être réécrite comme :

Selon la méthode similaire, les autres Eqs. 2 ~ 4 peuvent être discrétisés comme :

En combinant les équations discrétisées. 7-10 avec la condition aux limites, le champ électrique et le champ magnétique peuvent être résolus par la méthode itérative. Dans cette étude, la structure du réseau de trous métalliques est placée au-dessus du QDIP conventionnel et, en tant que telle, la structure peut faciliter le couplage de la lumière via la diffusion de Bragg. La communication optique correspondante est ensuite calculée, ce qui peut être discuté dans la section suivante lorsque la condition de la transmission, de la réflexion et de l'absorption est donnée. De plus, sur la base de la relation entre l'absorption et l'efficacité quantique, la réactivité du QDIP peut être donnée. Pour être concret, aussi bien connu que la réactivité du QDIP en tant que paramètre de performance très important peut être calculée par le rapport du photocourant et de la puissance de la lumière incidente [24]. Ainsi, il peut être écrit comme :

où je _photo est le photocourant du QDIP, P est la puissance de la lumière incidente, g est le gain photoconducteur, e est la charge de l'électron, h est la constante de Planck, v est la fréquence de la lumière incidente, et η est l'efficacité quantique.

L'efficacité quantique peut être définie comme le rapport du nombre du trou électronique et celui de la photo incidente, qui dépend fortement de l'absorption du photodétecteur. En pratique, comme la lumière incidente éclaire directement la zone d'absorption, elle ne peut pas être complètement absorbée en raison de la réflexion de la couche de contact supérieure ou de la couche métallique [25, 26]. Ainsi, l'efficacité quantique du QDIP peut s'écrire :

où α ₀ W est le coefficient d'absorption du QDIP, α ₀ d est le coefficient d'absorption de la couche de contact incidente, r est le reflet de la couche incidente, respectivement.

Dans le QDIP, le gain photoconducteur peut être défini comme le rapport du temps de recombinaison des électrons d'un état étendu vers une boîte quantique τ _{la vie} au temps de transit des électrons à travers l'appareil τ _total , et il peut être affiché comme :

et à condition que le temps de transit sur une période de la couche composite de points quantiques soit considérablement plus petit que le temps de recombinaison d'un état étendu vers un point quantique [22, 27]_, le gain peut s'écrire :

où K est le nombre est la couche composite de points quantiques, L est la distance entre les couches de points quantiques, μ la mobilité des électrons, E est la densité de champ électrique à travers le QDIP, v _s est la vitesse de saturation des électrons, h _QD est la hauteur des points quantiques, ∑_QD est la densité de points quantiques dans chaque couche de points quantiques, a _QD est la taille latérale des points quantiques, et V _t est le taux de capture des électrons, respectivement.

Soumis Eq. (12) et les équations. (14) dans l'Éq. (11), nous pouvons obtenir la réactivité du QDIP, qui peut être représentée par :

Résultats et discussion

Sur la base de la conception du QDIP ci-dessus, si la lumière infrarouge incidente frappe le dessus de ces QDIP dans le z -axe directionnel, les photodétecteurs auront la réflexion et la transmission de la lumière incidente. L'absorptivité des photodétecteurs peut être déterminée en étudiant ces conditions de transmission optique de la lumière incidente, qui peuvent jouer un rôle très important dans l'évaluation des performances du photodétecteur. La figure 6 présente leurs conditions de réflexion du photodétecteur sans la matrice métallique (le QDIP classique) et celle avec la matrice métallique (le QDIP amélioré). Par rapport aux deux courbes de la figure 6, on peut constater que les valeurs de coefficient de réflexion du QDIP conventionnel sont légèrement inférieures à celles du QDIP amélioré en plus des valeurs individuelles dans les gammes de fréquences de 250 ~ 260 Thz et 279 ~ 293  Thz . En effet, en prenant comme exemple la valeur à la fréquence de 219 Thz, la valeur du coefficient de réflexion du QDIP classique est de -3,91 dB, tandis que le QDIP amélioré est aussi faible que -1,31 dB. Comme cela a été dit ci-dessus, le QDIP amélioré peut avoir une valeur légèrement plus élevée que le QDIP classique, mais on peut constater que l'absorption minimale du QDIP amélioré est bien inférieure à celle du QDIP classique. Pour être précis, l'absorption minimale du QDIP amélioré est de −16,17 dB à la fréquence de 255,10 Thz, alors que la valeur pour le QDIP classique est égale à −13,42 dB à 254,86 Thz. Le faible coefficient de réflexion du QDIP amélioré pourrait être attribué au coefficient d'absorption du métal plus élevé que celui du semi-conducteur pour la lumière infrarouge. L'absorption peut être calculée sur la base des contributions communes de la réflexion et de la transmission. La figure 7a représente le coefficient de transmission du QDIP conventionnel et leurs valeurs marquées en bleu sont clairement supérieures à celles du QDIP amélioré dans la plage de fréquences totale de 200 à 340  Thz. Par exemple, à la fréquence de 298 Thz, le coefficient de transmission du QDIP amélioré n'est que de −10,83 dB, ce qui est 1,60 fois inférieur à celui du QDIP classique, qui est de −4,15 dB. Selon la relation de compétition entre la transmission, la réflexion et l'absorption, la diminution du coefficient de transmission conduira à l'augmentation de l'absorption à condition d'ignorer les autres pertes de la lumière incidente.

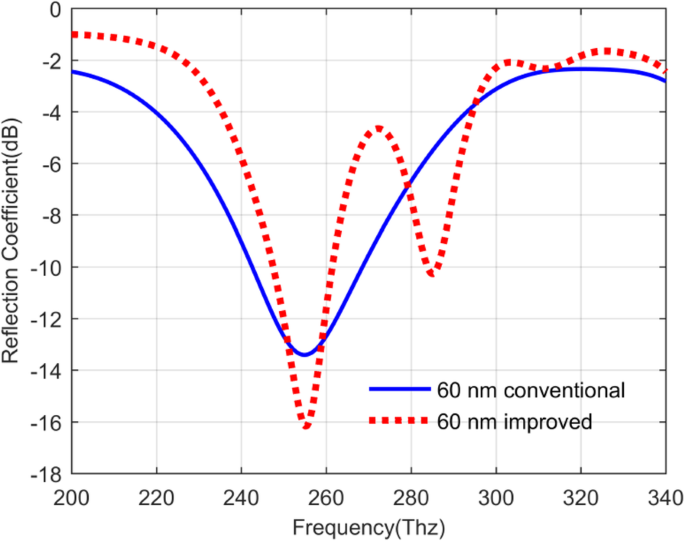
Coefficients de réflexion du QDIP conventionnel sans réseau métallique (courbe bleue) et du QDIP amélioré avec le réseau de nano-trous métalliques (courbe rouge)

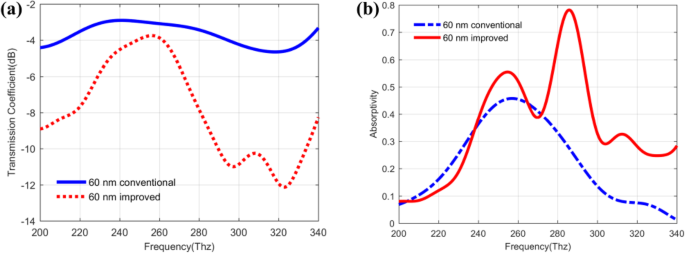
Coefficients de transmission (a ) et les coefficients d'absorptivité (b ) du QDIP conventionnel et du QDIP amélioré, respectivement

En combinant la situation de transmission sur la figure 7a avec la situation de réflexion sur la figure 6, l'absorptivité du QDIP peut être calculée, ce qui est montré sur la figure 7b. Sur la figure, la courbe rouge (marquée comme 60 nm améliorée) décrit l'absorptivité du QDIP amélioré avec la structure métallique, et l'autre courbe bleue représente la QDIP conventionnelle sans la structure à trous métalliques (marquée comme 60 nm conventionnelle). En comparant les deux courbes, on constate que l'absorptivité du QDIP amélioré est supérieure à celle du QDIP classique. Le maximum de l'absorptivité du QDIP amélioré est de 0,782 à la fréquence de 286 Thz, ce qui est 1,71 fois supérieur à celui du QDIP classique, qui n'est que de 0,458 à la fréquence de 257 Thz. Les raisons de l'augmentation de l'absorptivité du QDIP amélioré peuvent être expliquées comme suit. Les structures de réseau de nanotrous métalliques sont introduites sur le dessus du QDIP conventionnel, et une telle configuration peut favoriser l'effet de résonance plasmonique de surface, conduisant à l'effet de couplage local de la lumière incidente. De plus, l'effet de couplage local peut faire entrer plus de lumière incidente dans les couches de points quantiques semi-conducteurs ci-dessous, ce qui peut entraîner une absorption élevée de la lumière incidente et avoir de meilleures propriétés photoélectriques avec un photocourant plus important et une efficacité quantique plus élevée.

Pour préciser davantage comment réaliser l'effet d'amélioration du plasmon dans les QDIP améliorés, nous étudions également les influences des différentes structures de nanotrous métalliques sur l'absorptivité des QDIP améliorés. Comme le montre la figure 8a, les courbes d'absorptivité des QDIP améliorés avec différents rayons de nanotrous métalliques correspondent respectivement aux courbes noire (50 nm), verte (55 nm), rouge (60 nm) et bleue (65 nm). Les valeurs d'absorptivité du QDIP amélioré révèlent la tendance changeante différente sous différents nanotrous. Les valeurs maximales de l'absorptivité pour le QDIP amélioré sont de 0,744 (courbe noire à 289 Thz), 0,721 (courbe verte à 291 Thz), 0,782 (courbe rouge à 286 Thz) et 0,707 (courbe bleue à 288 Thz), respectivement. De toute évidence, parmi ces photodétecteurs, le QDIP amélioré avec un rayon de trou de 60 nm peut avoir les meilleures performances d'absorption. Dans le même temps, il est bien connu que l'épaisseur de la couche de trous métalliques peut également avoir des influences sur la capacité d'absorption. Comme le montre la figure 8b, lorsque l'épaisseur de la couche métallique dans le QDIP amélioré passe de 10 à 40 nm, les valeurs maximales de l'absorptivité passent de 0,667 (263  Thz pour l'épaisseur de 10 nm) à 0,782 (286 Thz pour 20 nm), 0,662 (293 Thz pour 30 nm) et 0,590 (262 Thz pour 40 nm). Parmi ces valeurs maximales, la couche de nanotrous métalliques d'une épaisseur de 20  nm peut avoir la valeur d'absorptivité la plus élevée.

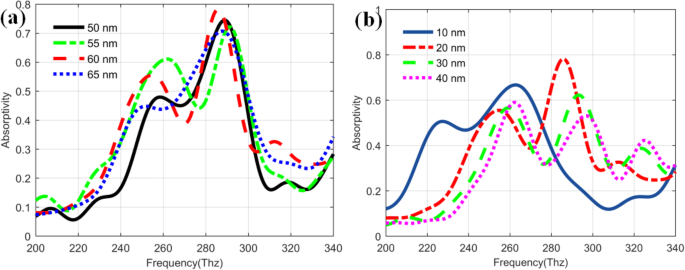
Absorptivité du QDIP amélioré (a ) avec différents rayons et différentes épaisseurs de métal de nanotrous métalliques (b)

Pour clarifier le phénomène ci-dessus, nous étudions plus en détail les conditions de distribution du champ électrique à la surface supérieure du QDIP amélioré avec les différents rayons des trous métalliques à 286 Thz. La figure 9 révèle la distribution du champ électrique à différents rayons de trous métalliques dans la plage de 50 à 65  nm. Par rapport aux quatre images de la figure 9a, il est clair que les QDIP avec un rayon de trou de 50 nm (Fig. 9a) et 55  nm (Fig. 9b) peuvent avoir une amélioration du champ électrique relativement plus faible en raison des distributions de champ électrique correspondantes dans Fig. 9 a et b se trouvant sur toute la zone, y compris les trous et leurs régions adjacentes, et donc leurs effets de couplage locaux de champ électrique peuvent être ignorés, tandis que la zone de couplage local du champ électrique avec un champ électrique élevé peut être observée sur la Fig. 9 c et d. Les fortes distributions de champ électrique autour des trous des figures 9c et d avec la forme de l'anneau peuvent être localisées à l'interface entre les trous métalliques et l'air dans les trous métalliques en raison de l'effet de couplage de plasmons de surface. Comparé aux distributions de champ électrique sur les figures 9c et d, l'effet de couplage de champ électrique sur la figure 9c est plus fort que celui sur la figure 9d en fonction de leurs couleurs marquées qui sont un mélange de rouge, vert et bleu. À cet égard, la couleur rouge représente le champ le plus fort et la couleur bleue représente le champ le plus faible. Sur la base de l'analyse ci-dessus, les nanotrous métalliques d'un rayon de 60  nm génèrent l'effet de champ électrique d'amélioration par le plasmon de surface. Pour rendre l'effet d'amélioration plus clair, la distribution du champ électrique sur xz -plan correspondant à l'absorption maximale du QDIP optimisé à la fréquence de 286 Thz dans notre étude comme le montre la Fig. 10a, qui se trouve sur la section y =0 (correspondant au champ du xz -avion). Sur la figure, depuis la direction de z -axe, la distribution de champ électrique améliorée se situe dans la région entre les trous métalliques adjacents qui est marquée par la couleur rouge et le champ faible se situe dans la région des trous métalliques marqués par la couleur bleue. La distribution du champ électrique révèle directement l'absorption accrue du QDIP. C'est l'effet de couplage d'amélioration qui conduit à l'augmentation de l'absorptivité, et conduit en outre à l'efficacité quantique élevée du QDIP amélioré. Bien entendu, les mêmes conclusions peuvent également être tirées en analysant la distribution du champ magnétique en fonction des propriétés des propriétés électromagnétiques de la lumière. En raison de la discussion de la distribution du champ magnétique est la même que celle de la distribution du champ électrique, il n'est pas nécessaire de discuter dans cette étude.

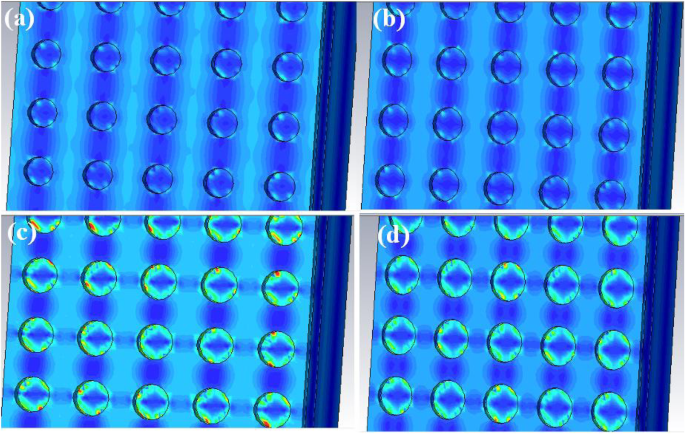
Distribution du champ électrique des QDIP améliorés avec différents rayons de nanotrous métalliques :a r =50 nm, b r =55 nm, c r =60 nm, et d r =65 nm

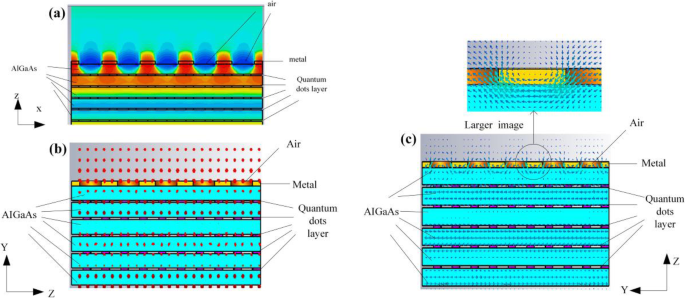
un x -direction du champ électrique du QDIP optimisé. b Polarisation du champ électrique du QDIP amélioré. c Polarisation du champ magnétique du QDIP amélioré

De plus, comme cela a été dit ci-dessus, l'effet d'amélioration provient du plasmon de surface, et le mode de l'onde de plasmon de surface excitée est en outre déterminé. Les figures 10a et b affichent les résultats des champs électriques et magnétiques. Sur la figure, la figure 10b présente la distribution de polarisation du champ électrique sur yz -avion. On peut voir que le champ électrique est normal au yz -plan, c'est-à-dire que le champ électrique ne peut pas avoir le E _z composant. La figure 10c présente la distribution de polarisation du champ magnétique. On peut constater que le champ magnétique est parallèle au yz -plan, c'est-à-dire qu'il y a la composante Hz dans la direction de propagation de la lumière incidente qui est z -direction. Ainsi, dans notre étude, l'onde plasmonique de surface excitée est le mode TE. De plus, pour préciser la position utilisée pour exciter le plasmon de surface, la distribution du champ magnétique près de l'interface du trou métallique est indiquée en haut de la figure 10c. On peut voir que le champ magnétique sur la position entre les trous métalliques adjacents est plus fort que celui dans les trous métalliques. De plus, selon le champ électrique apparaissant sur la figure 10a, cela peut également prouver que le champ d'amélioration est concentré sur l'emplacement entre les trous métalliques adjacents. Par conséquent, la conclusion peut être tirée que l'effet plasmon de surface peut provenir de la surface entre le métal et le semi-conducteur, qui se situe sur la position entre les trous métalliques adjacents. Bien sûr, il convient de noter que l'amélioration de l'absorption ne provient pas seulement du plasmon de surface mais également de la réflexion accrue de la couche métallique, conduisant à l'absorption secondaire de la lumière incidente puisque la lumière incidente est illuminée sur le QDIP le long axe z.

Il est bien connu que les paramètres liés aux couches métalliques peuvent également avoir une grande influence sur les performances du QDIP. Afin de déterminer les paramètres optimaux, l'épaisseur de la couche barrière et la couche de points quantiques sont analysées plus en détail et discutées dans les conditions d'épaisseur de couche métallique optimisée (20 nm) et de rayon de trou métallique (60 nm). La figure 11a illustre la tendance changeante de l'absorptivité des photodétecteurs avec les différentes épaisseurs de la couche barrière dans la plage de 70 à 85  nm. D'après l'image, ces courbes d'absorptivité ont une tendance de changement similaire. Lorsque les épaisseurs de la couche barrière varient dans la plage de 70 à 85 nm, les valeurs d'absorptivité maximales correspondantes des QDIP améliorés sont de 0,7581 (70  nm, à 322,78  Thz), 0,7763 (75  nm, à 304,84  Thz), 0,8552 (80 nm, à 292,75 Thz) et 0,8346 (85  nm, à 284,17), respectivement. Par rapport à ces valeurs d'absorptivité maximales, on peut constater que la couche barrière d'une épaisseur de 80  nm peut avoir les meilleures performances d'absorptivité pour les QDIP améliorés. D'autres paramètres fixes avec les valeurs optimisées ci-dessus, les influences des épaisseurs de la couche de points quantiques sur les performances d'absorptivité pour le QDIP amélioré sont étudiées plus avant, et les courbes correspondantes sont illustrées sur la figure 11b. D'après la figure, on peut constater que la courbe rouge peut avoir la valeur d'absorptivité maximale de 0,8647 à la fréquence de 295,48  Thz pour le QDIP amélioré avec une épaisseur de couche de 7  nm, ce qui illustre que le photodétecteur peut avoir l'état de transition optimal.

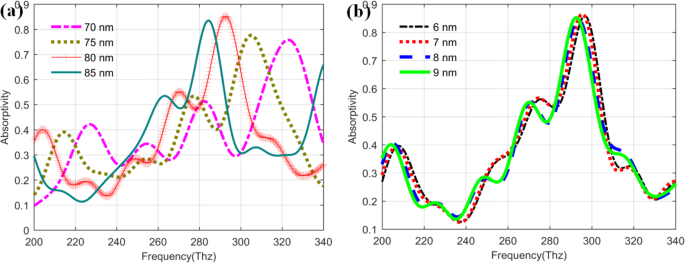
Absorptivité du QDIP amélioré avec les différentes épaisseurs de a la couche de points quantiques et b couche barrière

Sur la base de la discussion ci-dessus, il est clair que non seulement les paramètres liés au QDIP peuvent avoir une influence sur les performances du dispositif, mais également les épaisseurs de la couche de points quantiques et de la couche barrière peuvent également déterminer les performances du dispositif. Dans cette étude, selon les résultats des calculs théoriques, les paramètres optimisés pour les QDIP améliorés peuvent être donnés avec l'épaisseur de la couche métallique de 20 nm, le rayon du trou métallique de 60 nm, l'épaisseur de la couche de points quantiques de 7 nm et la couche barrière épaisseur de 80 nm. L'absorptivité du photodétecteur optimal peut atteindre 0,8647. De plus, en comparant le QDIP conventionnel avec le QDIP optimisé comme le montre la figure 12, les valeurs d'absorptivité dans la courbe rouge sont bien plus élevées que celles de la courbe bleue en plus des valeurs dans la plage de fréquences de 222,91 à 262,18  Thz. L'absorptivité maximale dans la courbe rouge est égale à 0,8647 à la fréquence de 295,48 Thz, ce qui est 1,89 fois plus grande que celle de la courbe bleue (qui est la même que la courbe précédente marquée "60 nm conventionnel" sur la Fig. 7b correspondant à le QDIP sans matrice de trous métalliques) à la fréquence de 257 Thz. Le décalage de fréquence pour le pic d'absorptivité maximum résulte principalement du changement d'épaisseur du photodétecteur amélioré. Furthermore, based on the optimized parameters of the QDIPs, the thicknesses of the quantum dot layer and the barrier layer, the quantum efficiency value and the responsivity of the photodetector are calculated out.

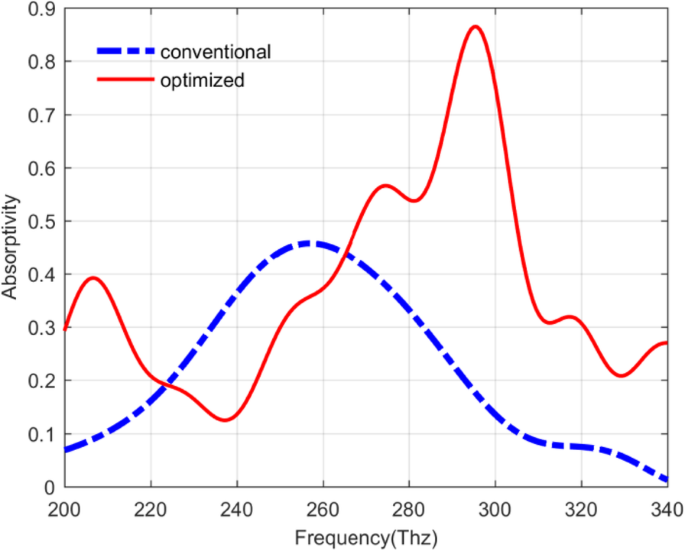
Absorptivity of the conventional QDIP in blue curve and improved QDIP in red curve with the barrier layer thickness of 80 nm

Quantum Efficiency and Responsivity of the QDIP

Based on the calculated results of the absorptivity in Fig. 12 as well as combining with the expression of the quantum efficiency and the responsivity of the QDIP above, the quantum efficiency of the QDIP and the responsivity can be calculated out, and the corresponding results are plotted in Fig. 13 a and b. Figure 13a depicts the quantum efficiency of the QDIP. In this figure, the blue dotted curve represents the quantum efficiency of the QDIP without metal array, the other red full curve is that of the optimized QDIP with metal array. Making a comparison between the two curves, it can be observed that the maximum quantum efficiency of the optimized QDIP is 0.2961 at the frequency of 295.87 Thz, and it is 1.205 times than that of the conventional QDIP, which is equal to 0.2458 at the frequency of 256.48 Thz. The increasing trend is similar to the absorptivity provided in Fig. 12 which results from the introduction of the metal hole array and the optimization of the quantum dot infrared photodetector. Based on the increasing trends for the absorptivity, we can find that the responsivity of the QDIP also reveals similar increasing trends. To be specific, Fig. 13b gives the responsivity of the optimized QDIP and the conventional QDIP, respectively. In the figure, the red curve is on behalf of the responsivity of the conventional QDIP, and the blue curve stands for that of the optimized QDIP with the metal holes layer. Similar to the analysis in Fig. 13a, the responsivity is 0.0326 mA/W at the frequency of 295.87 Thz, which is 0.0174 larger than that of the conventional QDIP at the frequency of 256.48 Thz (which is 0.0152). The increase in the responsivity can be proven in the other frequency band in the range of 229.57~254.41 Thz, which obviously demonstrates the enhancement in the performance of the photodetector due to the introduction of the metal hole array and the optimization of the quantum dot regions. Moreover, the reasons for the enhancement were detailedly discussed in detail analyzing the electric field distribution of quantum dot regions above.

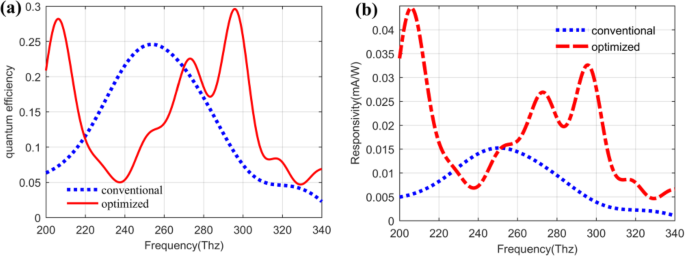
un Quantum efficiency of QDIP. b Responsivity of QDIP

Influence of the Electrodes and the Substrate

What was studied above is all under the condition of ignoring the influence of the electrodes and the substrate; in fact, the electrodes and the substrate can have certain influences on the performance, but they do not influence the description of the enhancement effects of the performance of the optimized QDIP with the metal layer. This is because the electrodes and the substrate can have almost the same influence on the absorption of the QDIP with the metal layer and without the metal layer. To illustrate the issue adequately, we recalculated the absorption of the QDIP considering the influence resulting from the substrate and the electrodes as well as the quantum efficiency, the responsivity, and so on. To be concrete, it is well known that the electrodes are generally designed at the two ends of the absorption region of the quantum dots, and thus, as shown in Fig. 14a, one is at the top of the conventional QDIP and the other is at the bottom end of the absorption region of the QDIP. That is to say, it lies at the top of the substrate, which can provide the quantum dot absorption region with the bias voltage and transmit current together with the electrodes said above. Here, it is worth mentioning that there is the metal hole array instead of the metal ring in the optimized QDIP in our study used as the electrodes. The other electrode is similar to that of conventional QDIP. Based on the above design, a concrete distribution of the electrodes is clearly calculated in Fig. 14a. Similar to Fig. 14a, in Fig. 14 b, the material of the electrodes is chosen as gold, and the substrate is chosen as AlGaAs; their thicknesses are 20 nm and 300 nm, respectively.

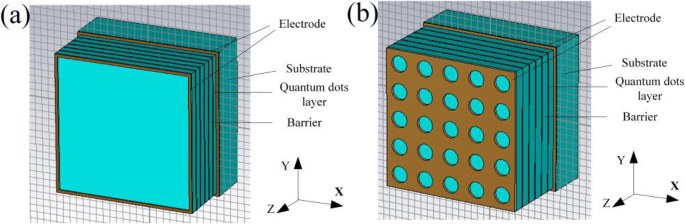
un Conventional QDIP with electrodes and substrate. b Optimized QDIP with the electrodes and substrate

Based on the introduction of electrodes and substrate in the structure of the QDIP above, we calculated the absorption of the QDIPs, and the corresponding results are compared with the QDIP without the electrodes and the substrate. Figure 15 demonstrates the influence of the electrodes and substrate on the absorptivity of the QDIP. In the figure, the blue curve and the pink curve are the absorptivity of the conventional QDIP without the electrodes and the substrate and that of the optimized QDIP without the electrodes and the substrate, respectively. The red dashed curve represents the absorptivity of the optimized QDIP with the electrodes and the substrate. Its maximum absorption is 0.7620 at the frequency of 304.35 Thz which is just 0.1027 smaller than that of the optimized QDIP without electrodes and substrate. The decrease of the absorptivity is degraded from the loss of the electrodes and the substrate, the same as the green curve with the absorptivity of the conventional QDIP with the electrodes and substrate. Compared with the absorptivity of the conventional QDIP and optimized QDIP with electrodes and substrate, the enhancement is very clear in the absorptivity of the optimized QDIP with electrodes and substrate, which is the same as the optimized QDIP in Fig. 12. In other words, though the electrodes and the substrate can result in the decrease of the absorptivity, the total absorptivity of the optimized QDIP can be enhanced compared with that of bare QDIP, and thus, the decrease can be negligible as they can have a very small influence on the description of the enhancement of the optimized QDIP when using the metal hole array.

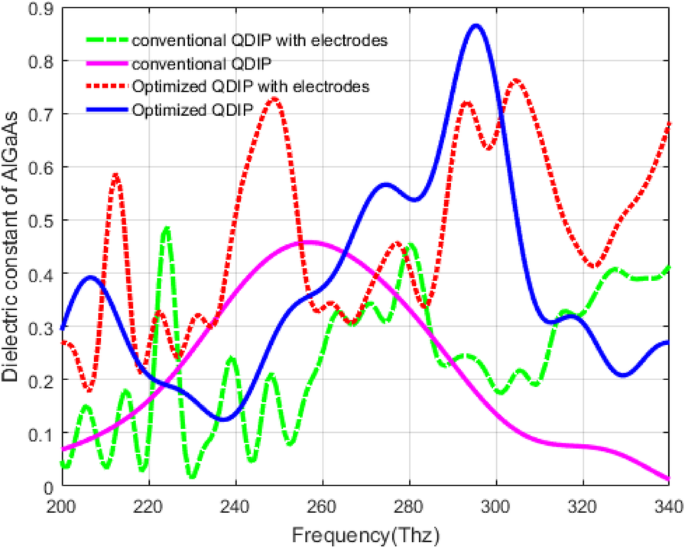
Absorption of the QDIP with electrodes and substrate

In addition, it can be observed that the change trend of the absorptivity of the QDIP with the electrodes and substrate cannot be the same as the previous curves (corresponding to the blue curve and pink curve). They are more complex with many peak values. The reasons for this phenomenon can be explained as follows. First of all, the addition of the electrodes and the substrate can produce more or less a loss and the frequency shifts due to the accumulated heating effect and the other negative influence factors. Secondly, since the material of the electrodes is chosen as the metal, in the optimized QDIP with the electrodes and the substrate, it can result in enhanced reflection and enhanced surface plasmon. The two reasons commonly favor the enhancement of the absorptivity as demonstrated in Fig. 15.

Conclusions

In conclusion, the conventional QDIP performance can be greatly improved by adding the nanoscale metal nanohole array, and the enhanced mechanism of the performance for improved QDIPs is discussed by analyzing the reflection, the transmission, the absorption, and the distribution of the electric field. The results not only demonstrate that the improved QDIPs can have higher absorptivity than that of conventional QDIPs but also indicate that the parameters of the improved QDIPs related to the metal nanohole array together with the quantum dot composite layer can significantly influence their performance. According to theoretical calculation, the optimized parameters of the improved photodetectors are 20 nm in metal layer thickness, 60 nm in metal hole radius, 7 nm in quantum dot layer thickness, and 80 nm in barrier layer thickness. The maximum absorptivity value of the optimized photodetector can be as high as 86.47% at the frequency of ~ 300 Thz. The great enhancement of the absorptivity can be attributed to the local coupling effect caused by the enhancement of the electric field effect via the surface plasmon, and further leads to the high quantum efficiency and responsivity, which are 0.2961 and 0.0326 mA/W, respectively. It is believed that the current contribution could provide certain theoretical guidance for developing nanoscale QDIPs with high performance.

Disponibilité des données et des matériaux

Toutes les données sont entièrement disponibles sans restriction.

Abréviations

QDIPs:

Quantum dot infrared photodetectors

Fig

Chiffre

Eqs

Equations