Conversion de tables de vérité en expressions booléennes

Lors de la conception de circuits numériques, le concepteur commence souvent par une table de vérité décrivant ce que le circuit doit faire.

La tâche de conception consiste en grande partie à déterminer quel type de circuit exécutera la fonction décrite dans la table de vérité.

Alors que certaines personnes semblent avoir une capacité naturelle à regarder une table de vérité et à imaginer immédiatement la porte logique ou les circuits logiques de relais nécessaires pour la tâche, il existe des techniques procédurales disponibles pour le reste d'entre nous.

Ici, l'algèbre booléenne prouve son utilité de la manière la plus spectaculaire.

Pour illustrer cette méthode procédurale, nous devons commencer par un problème de conception réaliste.

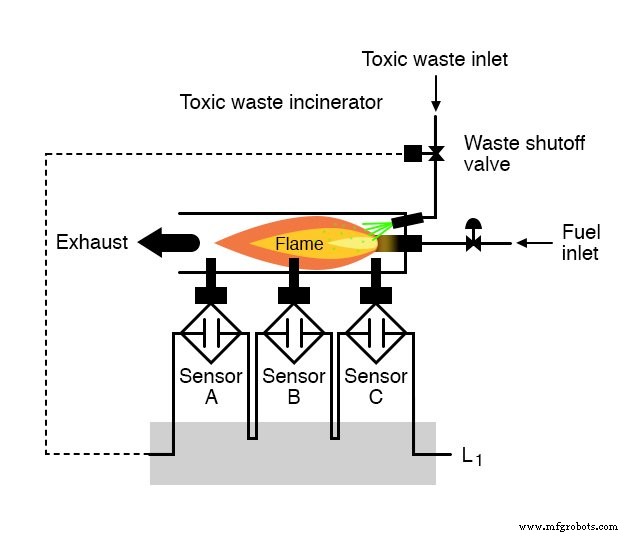
Supposons qu'on nous confie la tâche de concevoir un circuit de détection de flamme pour un incinérateur de déchets toxiques.

La chaleur intense du feu est destinée à neutraliser la toxicité des déchets introduits dans l'incinérateur.

Ces techniques basées sur la combustion sont couramment utilisées pour neutraliser les déchets médicaux, qui peuvent être infectés par des virus ou des bactéries mortelles :

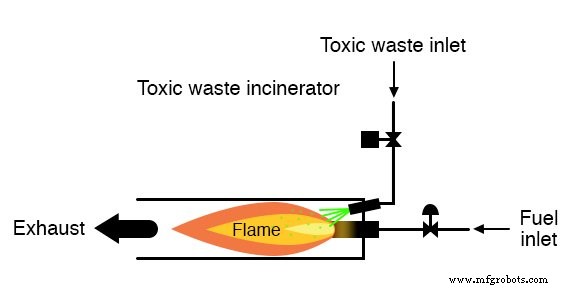
Tant qu'une flamme est maintenue dans l'incinérateur, il est sécuritaire d'y injecter des déchets à neutraliser.

Si la flamme devait être éteinte, cependant, il serait dangereux de continuer à injecter des déchets dans la chambre de combustion, car ils sortiraient de l'échappement non neutralisés et constitueraient une menace pour la santé de toute personne se trouvant à proximité de l'échappement.

Ce dont nous avons besoin dans ce système, c'est d'un moyen sûr de détecter la présence d'une flamme, et de permettre l'injection de déchets uniquement si une flamme est « prouvée » par le système de détection de flamme.

Plusieurs technologies différentes de détection de flamme existent :optique (détection de la lumière), thermique (détection de haute température) et conduction électrique (détection de particules ionisées dans le trajet de la flamme), chacune avec ses avantages et ses inconvénients uniques.

Supposons qu'en raison du degré élevé de risque lié au rejet potentiel de déchets non neutralisés par l'échappement de cet incinérateur, il soit décidé de rendre le système de détection de flamme redondant (plusieurs capteurs), de sorte que la défaillance d'un seul capteur n'entraîne pas à une émission de toxines à l'échappement.

Chaque capteur est équipé d'un contact normalement ouvert (ouvert si pas de flamme, fermé si flamme détectée) que nous utiliserons pour activer les entrées d'un système logique :

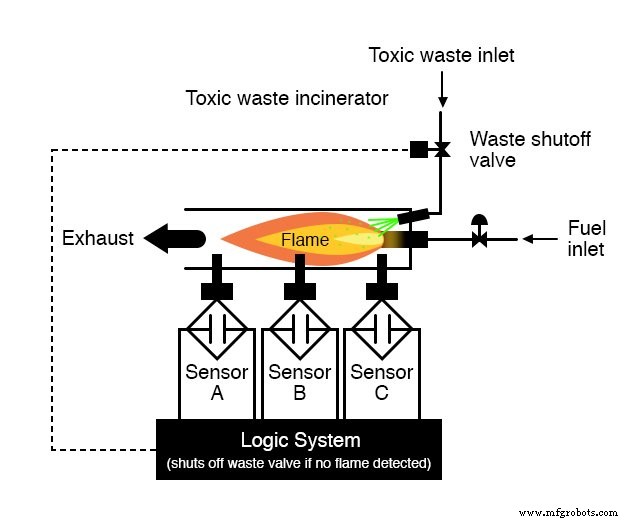
Notre tâche, maintenant, est de concevoir les circuits du système logique pour ouvrir la vanne de décharge si et seulement si les capteurs ont prouvé une bonne flamme.

Cependant, nous devons d'abord décider quel devrait être le comportement logique de ce système de contrôle.

Voulons-nous que la vanne soit ouverte si un seul des trois capteurs détecte une flamme ? Probablement pas, car cela irait à l'encontre de l'objectif d'avoir plusieurs capteurs.

Si l'un des capteurs tombait en panne de manière à indiquer faussement la présence d'une flamme alors qu'il n'y en avait pas, un système logique basé sur le principe « un des trois capteurs montrant une flamme » donnerait le même résultat que un système à capteur unique aurait le même échec.

Une bien meilleure solution serait de concevoir le système de sorte que la vanne soit commandée pour s'ouvrir si et seulement si les trois capteurs détecter une bonne flamme.

De cette façon, un seul capteur défaillant montrant faussement une flamme ne pouvait pas maintenir la vanne en position ouverte ; il faudrait plutôt que les trois capteurs tombent en panne de la même manière - un scénario hautement improbable - pour que cette condition dangereuse se produise.

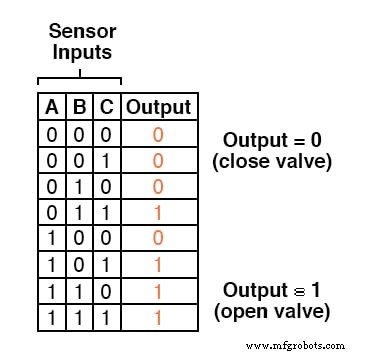
Ainsi, notre table de vérité ressemblerait à ceci :

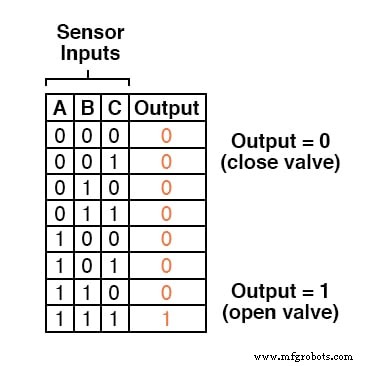
Il ne faut pas beaucoup de perspicacité pour se rendre compte que cette fonctionnalité pourrait être générée avec une porte ET à trois entrées :la sortie du circuit sera « haute » si et seulement si l'entrée A ET entrée B ET l'entrée C sont toutes « élevées » :

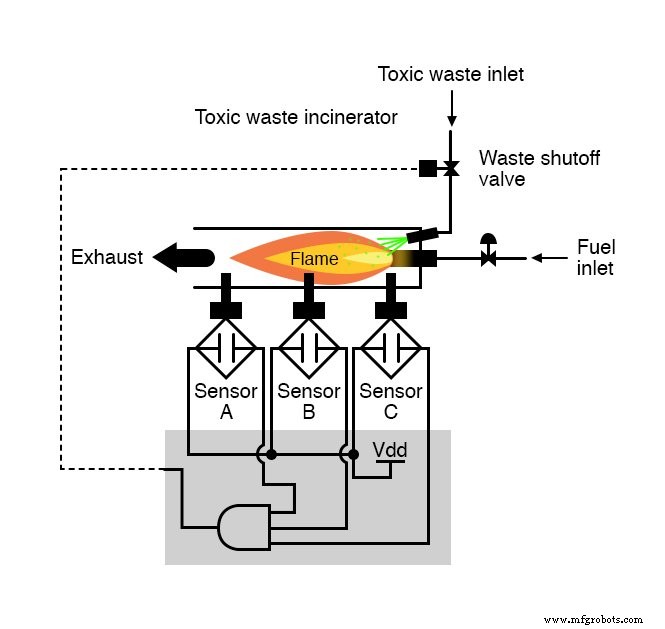
Si vous utilisez des circuits de relais, nous pourrions créer cette fonction ET en câblant trois contacts de relais en série, ou simplement en câblant les trois contacts de capteur en série, de sorte que la seule façon d'envoyer de l'énergie électrique pour ouvrir la vanne d'évacuation soit si les trois capteurs indiquer la flamme :

Bien que cette stratégie de conception maximise la sécurité, elle rend le système très sensible aux défaillances de capteurs de type opposé.

Supposons que l'un des trois capteurs tombe en panne de telle sorte qu'il n'indique aucune flamme alors qu'il y avait vraiment une bonne flamme dans la chambre de combustion de l'incinérateur.

Cette seule défaillance fermerait inutilement la vanne de décharge, ce qui entraînerait une perte de temps de production et de carburant (alimentant un feu qui n'était pas utilisé pour incinérer les déchets).

Ce serait bien d'avoir un système logique qui permette ce type de panne sans arrêter le système inutilement, tout en fournissant une redondance des capteurs afin de maintenir la sécurité au cas où un seul capteur tomberait en panne « haut » (montrant une flamme à tout moment , qu'il y en ait ou non un à détecter).

Une stratégie qui répondrait aux deux besoins serait une logique de capteur « deux sur trois », selon laquelle la vanne d'évacuation est ouverte si au moins deux des trois capteurs montrent une bonne flamme.

La table de vérité pour un tel système ressemblerait à ceci :

Utiliser la somme des produits

Ici, il n'est pas forcément évident de savoir quel type de circuit logique satisferait à la table de vérité.

Cependant, une méthode simple pour concevoir un tel circuit se trouve dans une forme standard d'expression booléenne appelée Sum-Of-Products , ou SOP , former.

Comme vous vous en doutez, une expression booléenne Sum-Of-Products est littéralement un ensemble de termes booléens ajoutés (sommés ) ensemble, chaque terme étant un multiplicatif (produit ) combinaison de variables booléennes.

Un exemple d'expression SOP serait quelque chose comme ceci :ABC + BC + DF, la somme des produits « ABC », « BC » et « DF ».

Les expressions Sum-Of-Products sont faciles à générer à partir de tables de vérité.

Tout ce que nous avons à faire est d'examiner la table de vérité pour toutes les lignes où la sortie est « élevée » (1) et d'écrire un terme de produit booléen qui équivaudrait à une valeur de 1 compte tenu de ces conditions d'entrée.

Par exemple, dans la quatrième ligne du bas de la table de vérité pour notre système logique deux sur trois, où A=0, B=1 et C=1, le terme produit serait A'BC, puisque ce terme aurait une valeur de 1 si et seulement si A=0, B=1 et C=1 :

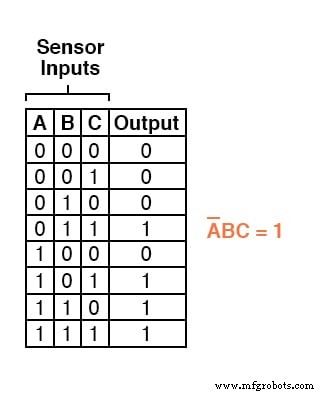
Trois autres lignes de la table de vérité ont une valeur de sortie de 1, ces lignes ont donc également besoin d'expressions de produits booléens pour les représenter :

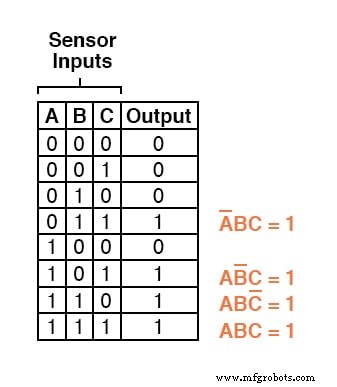
Enfin, nous joignons ces quatre expressions de produit booléen par addition, pour créer une seule expression booléenne décrivant la table de vérité dans son ensemble :

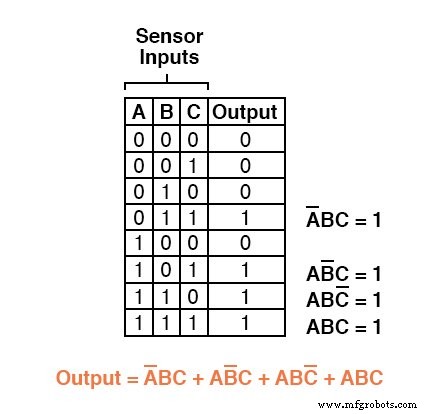
Maintenant que nous avons une expression booléenne Sum-Of-Products pour la fonction de la table de vérité, nous pouvons facilement concevoir une porte logique ou un circuit logique de relais basé sur cette expression :

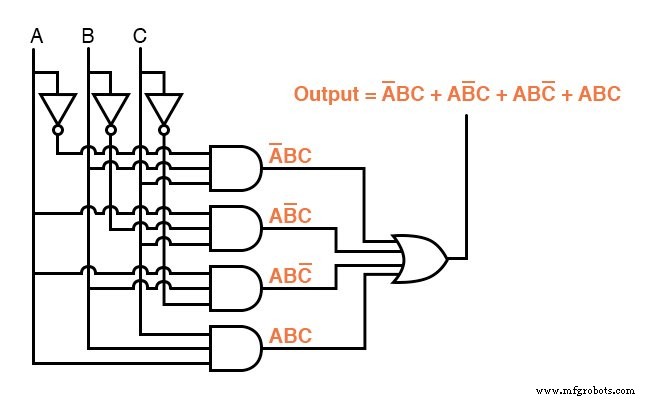
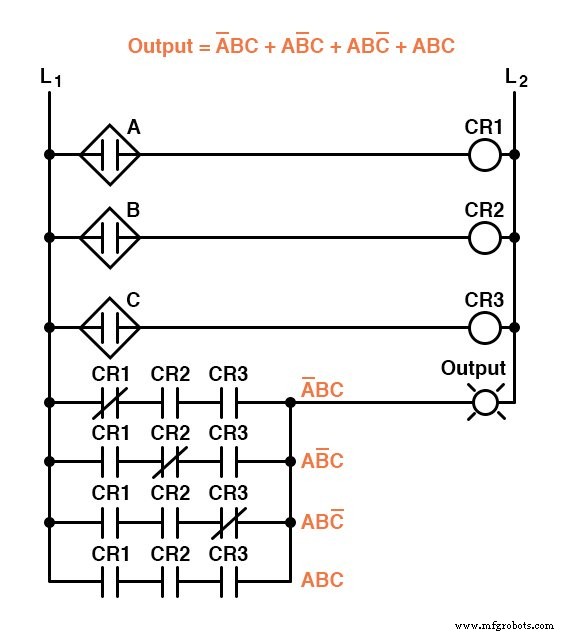
Malheureusement, ces deux circuits sont assez complexes et pourraient gagner à être simplifiés.

En utilisant des techniques d'algèbre booléenne, l'expression peut être considérablement simplifiée :

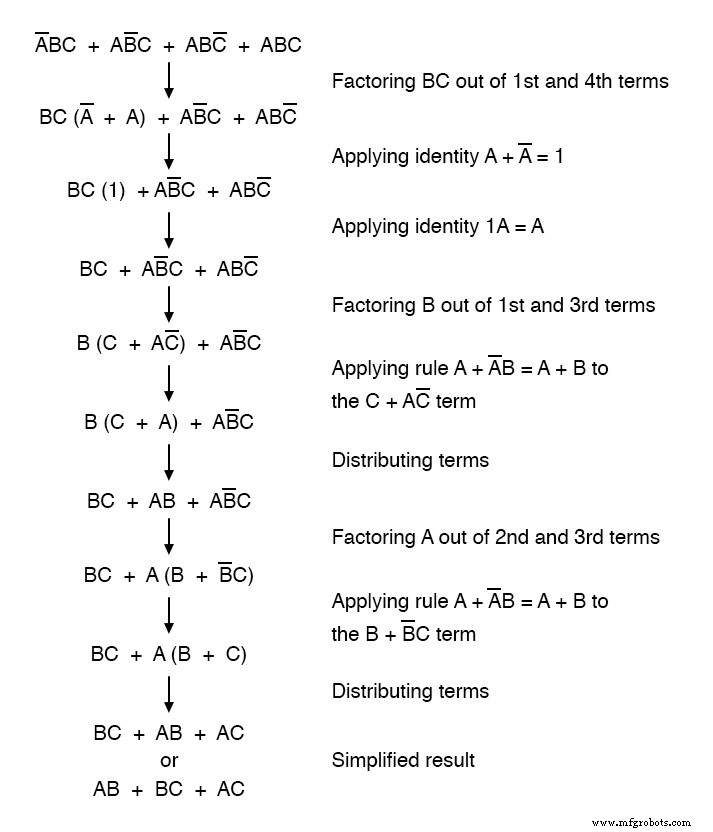
Grâce à la simplification, nous pouvons maintenant construire des circuits logiques beaucoup plus simples remplissant la même fonction, sous forme de porte ou de relais :

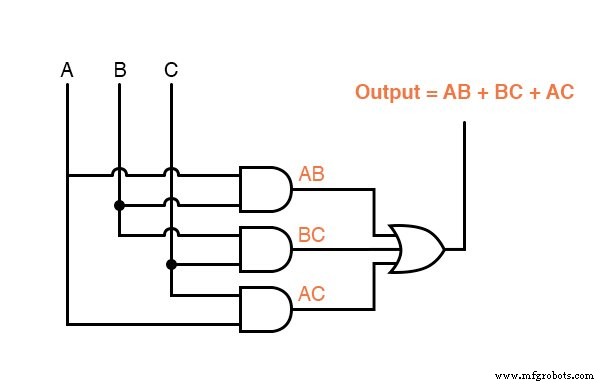
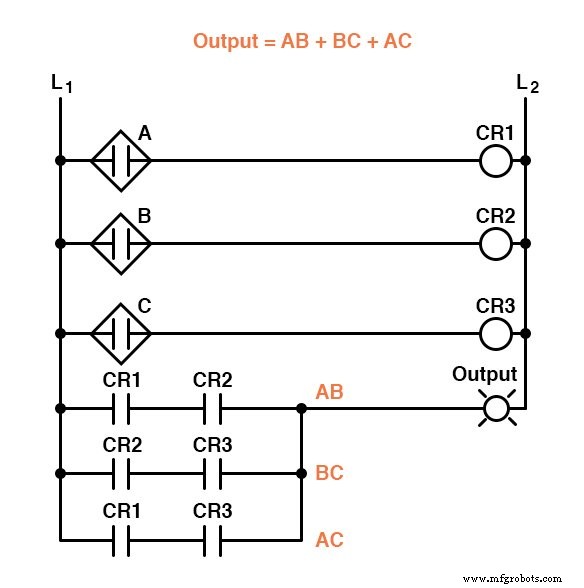
L'un ou l'autre de ces circuits effectuera correctement la tâche de fonctionnement de la vanne d'évacuation de l'incinérateur sur la base d'une vérification de flamme à partir de deux des trois capteurs de flamme.

Au minimum, c'est ce dont nous avons besoin pour avoir un système d'incinération sûr.

Nous pouvons cependant étendre les fonctionnalités du système en y ajoutant des circuits logiques conçus pour détecter si l'un des capteurs n'est pas d'accord avec les deux autres.

Si les trois capteurs fonctionnent correctement, ils devraient détecter la flamme avec la même précision.

Ainsi, ils doivent soit tous enregistrer « bas » (000 :pas de flamme) soit tous enregistrer « haut » (111 :bonne flamme).

Toute autre combinaison de sorties (001, 010, 011, 100, 101 ou 110) constitue un désaccord entre les capteurs et peut donc servir d'indicateur d'une défaillance potentielle du capteur.

Si nous ajoutions des circuits pour détecter l'une des six conditions de « désaccord du capteur », nous pourrions utiliser la sortie de ces circuits pour activer une alarme.

Celui qui surveille l'incinérateur exercerait alors son jugement soit en continuant à fonctionner avec un éventuel capteur défaillant (entrées :011, 101 ou 110), soit en arrêtant l'incinérateur pour être absolument sûr.

De plus, si l'incinérateur est arrêté (pas de flamme) et qu'un ou plusieurs capteurs indiquent toujours une flamme (001, 010, 011, 100, 101 ou 110) tandis que l'autre ou les autres indiquent l'absence de flamme, on saura qu'il existe un problème certain de capteur.

La première étape de la conception de ce circuit de détection de « désaccord du capteur » consiste à écrire une table de vérité décrivant son comportement.

Puisque nous avons déjà une table de vérité décrivant la sortie du circuit logique « bonne flamme », nous pouvons simplement ajouter une autre colonne de sortie à la table pour représenter le deuxième circuit, et créer une table représentant l'ensemble du système logique :

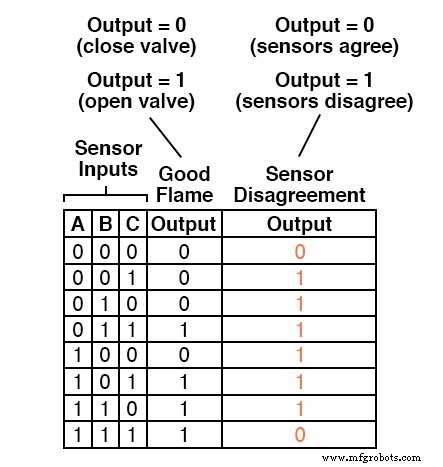
Bien qu'il soit possible de générer une expression Sum-Of-Products pour cette nouvelle colonne de table de vérité, cela nécessiterait six termes, de trois variables chacun !

Une telle expression booléenne nécessiterait de nombreuses étapes pour être simplifiée, avec un grand potentiel d'erreurs algébriques :

Utiliser le produit des sommes

Une alternative à la génération d'une expression Sum-Of-Products pour tenir compte de toutes les conditions de sortie « élevées » (1) dans la table de vérité consiste à générer un Product-Of-Sums , ou POS , expression, pour tenir compte de toutes les conditions de sortie « faibles » (0) à la place.

Étant donné qu'il y a beaucoup moins d'instances de sortie « faible » dans la dernière colonne de la table de vérité, l'expression Product-Of-Sums résultante devrait contenir moins de termes.

Comme son nom l'indique, une expression Product-Of-Sums est un ensemble de termes ajoutés (sommes ), qui sont multipliés (produit ) ensemble.

Un exemple d'expression POS serait (A + B)(C + D), le produit des sommes "A + B" et "C + D".

Pour commencer, nous identifions quelles lignes de la dernière colonne de la table de vérité ont des sorties « faibles » (0) et écrivons un terme de somme booléenne qui serait égal à 0 pour les conditions d'entrée de cette ligne.

Par exemple, dans la première ligne de la table de vérité, où A=0, B=0 et C=0, le terme somme serait (A + B + C), puisque ce terme aurait une valeur de 0 si et uniquement si A=0, B=0 et C=0 :

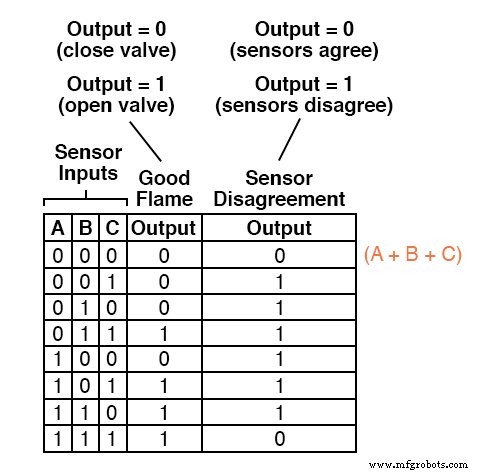
Une seule autre ligne de la dernière colonne de la table de vérité a une sortie "faible" (0), donc tout ce dont nous avons besoin est un terme de somme supplémentaire pour compléter notre expression Product-Of-Sums.

Ce dernier terme somme représente une sortie 0 pour une condition d'entrée de A=1, B=1 et C=1.

Par conséquent, le terme doit être écrit comme (A' + B'+ C'), car seule la somme des complétés les variables d'entrée seraient égales à 0 pour cette condition uniquement :

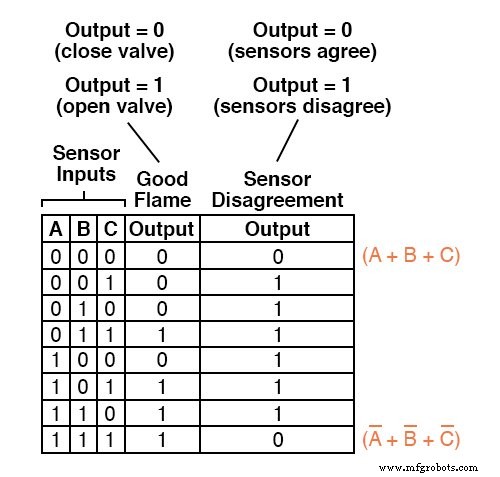
L'expression Product-Of-Sums terminée, bien sûr, est la combinaison multiplicative de ces deux termes de somme :

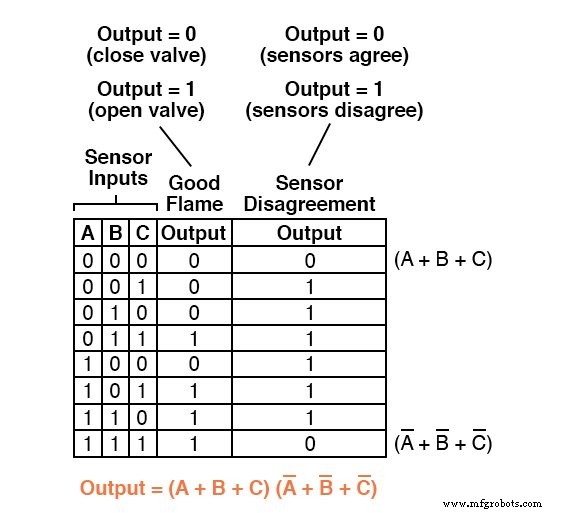
Alors qu'une expression Sum-Of-Products pourrait être implémentée sous la forme d'un ensemble de portes ET avec leurs sorties connectées à une seule porte OU, une expression Product-Of-Sums peut être implémentée comme un ensemble de portes OU alimentant un seul ET porte :

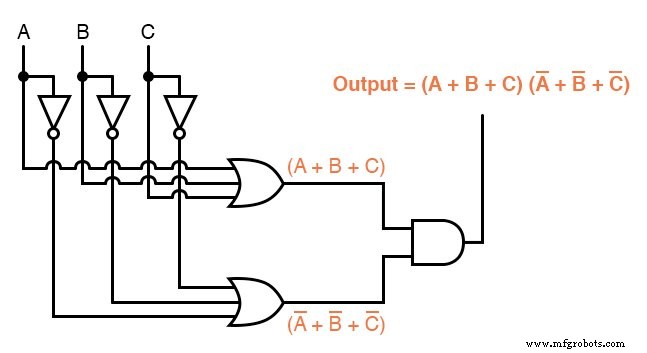
En conséquence, alors qu'une expression Sum-Of-Products peut être implémentée comme une collection parallèle de contacts de relais connectés en série, une expression Product-Of-Sums peut être implémentée comme une collection de séries de contacts de relais connectés en parallèle :

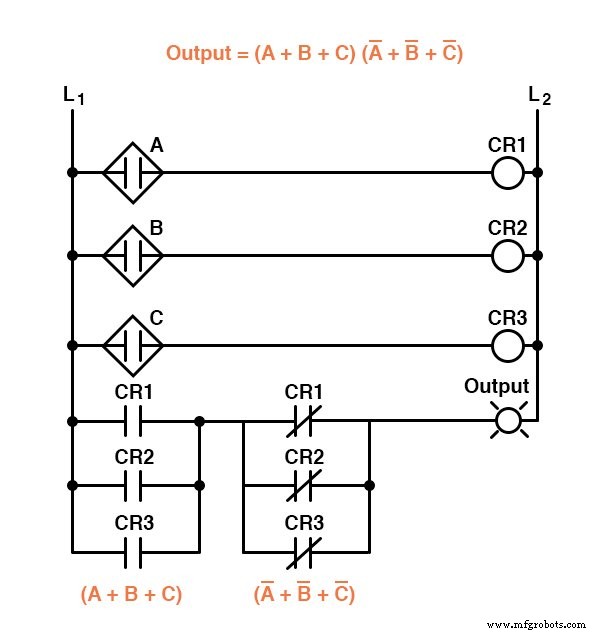
Les deux circuits précédents représentent des versions différentes du circuit logique de « désaccord du capteur » uniquement, pas le ou les circuits de détection de « bonne flamme ».

L'ensemble du système logique serait la combinaison des circuits « bonne flamme » et « désaccord du capteur », illustrés sur le même schéma.

Implémenté dans un contrôleur logique programmable (PLC), l'ensemble du système logique pourrait ressembler à quelque chose comme ceci :

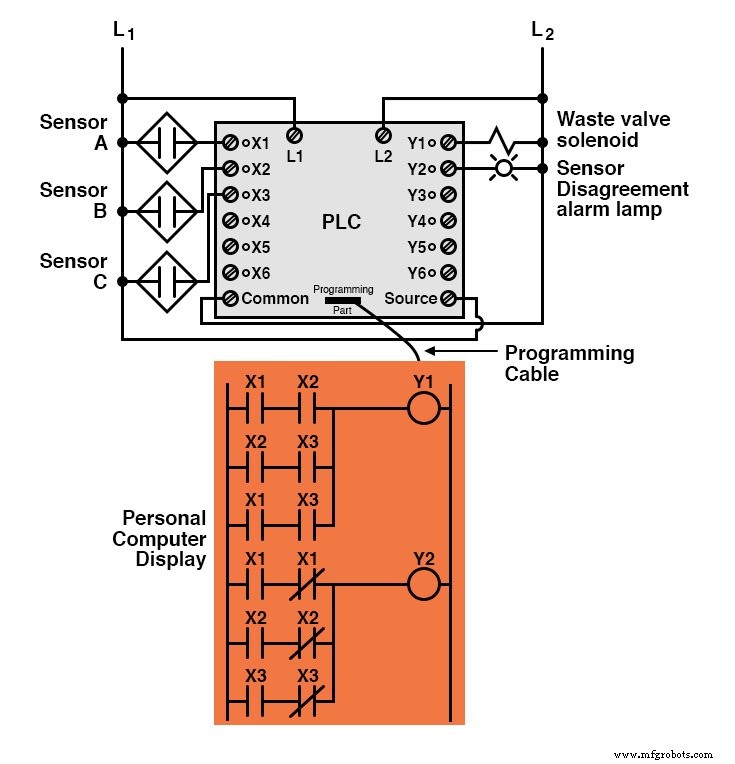
Comme vous pouvez le voir, les formulaires booléens standard Sum-Of-Products et Products-Of-Sums sont des outils puissants lorsqu'ils sont appliqués aux tables de vérité.

Ils nous permettent de dériver une expression booléenne - et finalement, un circuit logique réel - à partir d'une table de vérité, qui est une spécification écrite de ce que nous voulons qu'un circuit logique fasse.

Pouvoir passer d'une spécification écrite à un circuit réel en utilisant des procédures simples et déterministes signifie qu'il est possible d'automatiser le processus de conception d'un circuit numérique.

En d'autres termes, un ordinateur pourrait être programmé pour concevoir un circuit logique personnalisé à partir d'une spécification de table de vérité !

Les étapes à franchir d'une table de vérité au circuit final sont si claires et directes qu'elles nécessitent peu, voire aucune, créativité ou autre réflexion originale pour les exécuter.

AVIS :

• Somme des produits , ou SOP , les expressions booléennes peuvent être générées assez facilement à partir des tables de vérité, en déterminant quelles lignes de la table ont une sortie de 1, en écrivant un terme de produit pour chaque ligne, et enfin en additionnant tous les termes de produit. Cela crée une expression booléenne représentant la table de vérité dans son ensemble.
• Les expressions Sum-Of-Products se prêtent bien à la mise en œuvre en tant qu'ensemble de portes ET (produits) alimentant une seule porte OU (somme).
• Produit-De-Sommes , ou POS , les expressions booléennes peuvent également être générées assez facilement à partir des tables de vérité, en déterminant quelles lignes de la table ont une sortie de 0, en écrivant un terme de somme pour chaque ligne, et enfin en multipliant tous les termes de somme. Cela crée une expression booléenne représentant la table de vérité dans son ensemble.
• Les expressions Product-Of-Sums se prêtent bien à la mise en œuvre en tant qu'ensemble de portes OU (sommes) alimentant une seule porte ET (produit).

FICHES DE TRAVAIL CONNEXES :

• Fiche de travail sur les expressions de somme de produits et de produit de somme
• Feuille de travail d'algèbre booléenne