Théorèmes de DeMorgan

Un mathématicien nommé DeMorgan a développé une paire de règles importantes concernant la complémentation des groupes en algèbre booléenne.

Par groupe complémentation, je fais référence au complément d'un groupe de termes, représenté par une longue barre sur plus d'une variable.

Vous devez vous rappeler du chapitre sur les portes logiques que l'inversion de toutes les entrées vers une porte inverse la fonction essentielle de cette porte de ET à OU, ou vice versa, et inverse également la sortie.

Ainsi, une porte OU avec toutes les entrées inversées (une porte OU négatif) se comporte de la même manière qu'une porte NAND, et une porte ET avec toutes les entrées inversées (une porte ET négatif) se comporte de la même manière qu'une porte NOR.

Les théorèmes de DeMorgan déclarent la même équivalence sous une forme « à l'envers » :l'inversion de la sortie de n'importe quelle porte entraîne la même fonction que le type de porte opposé (ET contre OU) avec des entrées inversées :

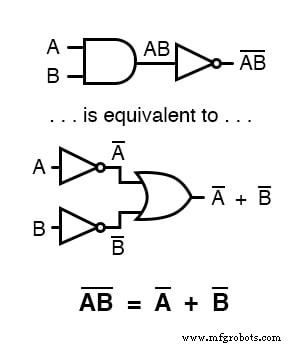
Une longue barre s'étendant sur le terme AB agit comme un symbole de regroupement et, en tant que telle, est entièrement différente du produit de A et B inversé indépendamment.

En d'autres termes, (AB)' n'est pas égal à A'B'. Parce que le symbole "premier" (') ne peut pas être étiré sur deux variables comme une barre, nous sommes obligés d'utiliser des parenthèses pour qu'il s'applique à l'ensemble du terme AB dans la phrase précédente.

Une barre, cependant, agit comme son propre symbole de regroupement lorsqu'elle est étirée sur plus d'une variable.

Cela a un impact profond sur la façon dont les expressions booléennes sont évaluées et réduites, comme nous le verrons.

Théorème de DeMorgan

Le théorème de DeMorgan peut être considéré en termes de rupture un long symbole de barre.

Lorsqu'une longue barre est cassée, l'opération directement sous la rupture passe de l'addition à la multiplication, ou vice versa, et les morceaux de barre cassés restent sur les variables individuelles. Pour illustrer :

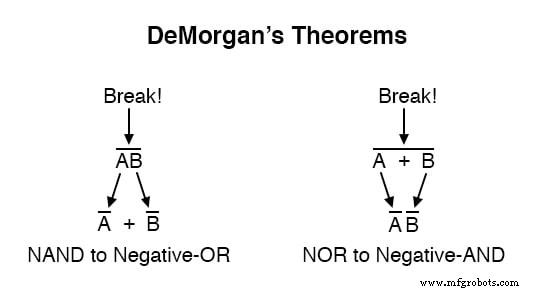
Lorsque plusieurs « couches » de barres existent dans une expression, vous ne pouvez briser une barre à la fois , et il est généralement plus facile de commencer la simplification en cassant d'abord la barre la plus longue (la plus haute).

Pour illustrer, prenons l'expression (A + (BC)')' et réduisons-la en utilisant les théorèmes de DeMorgan :

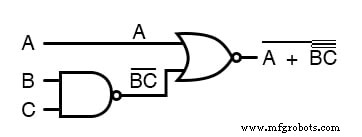
En suivant le conseil de briser d'abord la barre la plus longue (la plus haute), je commencerai par briser la barre couvrant l'ensemble de l'expression dans un premier temps :

En conséquence, le circuit d'origine est réduit à une porte ET à trois entrées avec l'entrée A inversée :

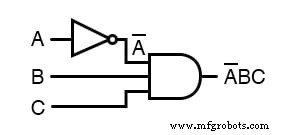
Vous ne devriez jamais casser plus d'une barre en une seule étape, comme illustré ici :

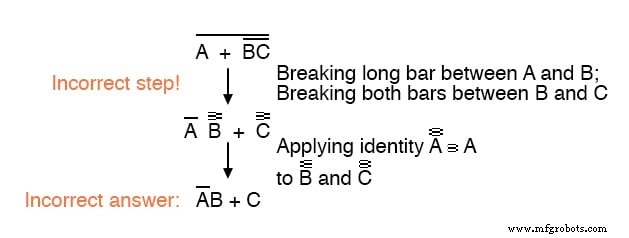
Aussi tentant que cela puisse être de conserver des pas et de casser plus d'une barre à la fois, cela conduit souvent à un résultat incorrect, alors ne le faites pas !

Il est possible de réduire correctement cette expression en cassant d'abord la barre courte plutôt que la barre longue en premier :

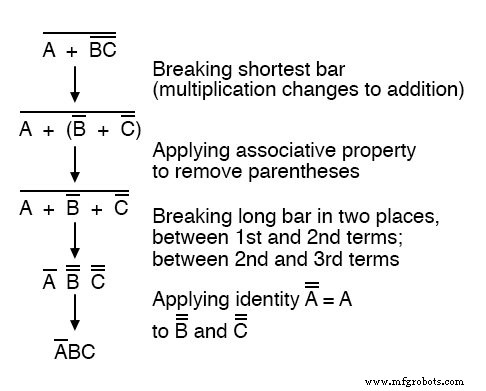
Le résultat final est le même, mais plus d'étapes sont nécessaires par rapport à l'utilisation de la première méthode, où la barre la plus longue a été brisée en premier.

Notez comment dans la troisième étape, nous avons cassé la barre longue à deux endroits.

C'est une opération mathématique légitime, et pas la même chose que de casser deux barres en une seule étape !

L'interdiction de casser plus d'une barre en une seule étape n'est pas une interdiction de casser une barre à plus d'un endroit.

Rupture à plus d'un endroit en une seule étape c'est bien; casser plus d'une barre en une seule étape n'est pas.

Vous vous demandez peut-être pourquoi des parenthèses ont été placées autour de la sous-expression B' + C', étant donné que je viens de les supprimer à l'étape suivante.

J'ai fait cela pour souligner un aspect important mais facilement négligé du théorème de DeMorgan.

Puisqu'une longue barre fonctionne comme un symbole de regroupement, les variables précédemment groupées par une barre brisée doivent rester groupées de peur que la priorité appropriée (ordre d'opération) ne soit perdue.

Dans cet exemple, cela n'aurait aucune importance si j'oubliais de mettre des parenthèses après avoir brisé la barre courte, mais dans d'autres cas, cela pourrait le faire.

Considérez cet exemple, en commençant par une expression différente :

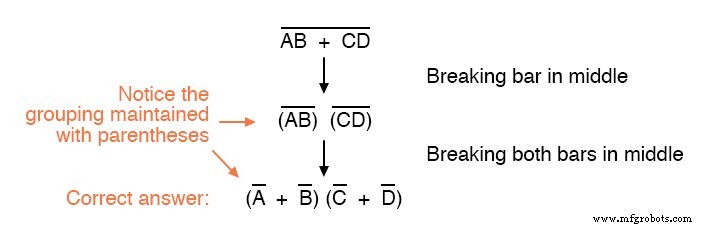
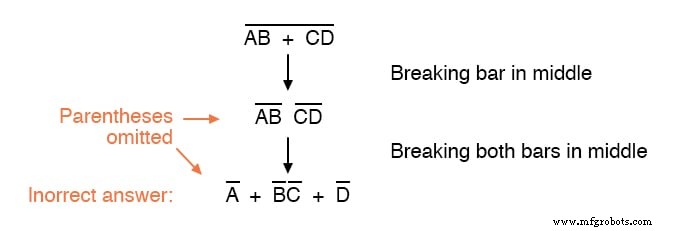
Comme vous pouvez le voir, le maintien du regroupement impliqué par les barres de complémentation pour cette expression est crucial pour obtenir la bonne réponse.

Appliquons les principes des théorèmes de DeMorgan à la simplification d'un circuit de porte :

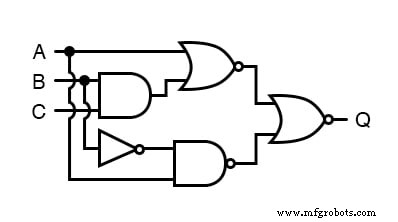
Comme toujours, notre première étape pour simplifier ce circuit doit être de générer une expression booléenne équivalente.

Nous pouvons le faire en plaçant une étiquette de sous-expression à la sortie de chaque porte, à mesure que les entrées deviennent connues. Voici la première étape de ce processus :

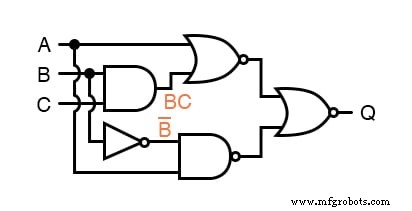
Ensuite, nous pouvons étiqueter les sorties de la première porte NOR et de la porte NAND.

Lorsqu'il s'agit de portes à sortie inversée, je trouve qu'il est plus facile d'écrire une expression pour la sortie de la porte sans l'inversion finale, avec une flèche pointant juste avant la bulle d'inversion.

Ensuite, au niveau du fil sortant de la porte (après la bulle), j'écris l'expression complète et complétée.

Cela permet de garantir que je n'oublie pas une barre complémentaire dans la sous-expression, en m'obligeant à diviser la tâche d'écriture d'expression en deux étapes :

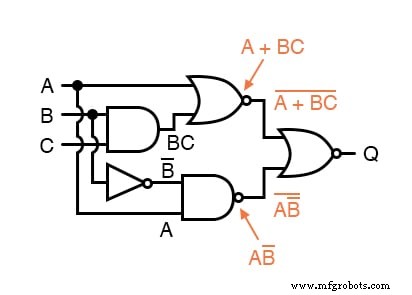
Enfin, nous écrivons une expression (ou une paire d'expressions) pour la dernière porte NOR :

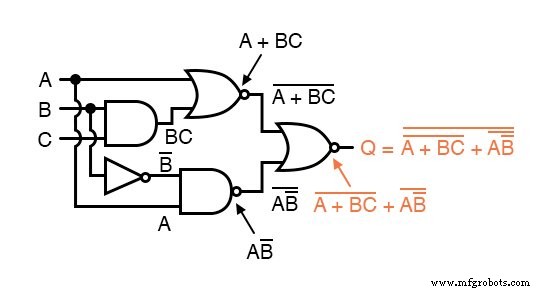
Maintenant, nous réduisons cette expression en utilisant les identités, propriétés, règles et théorèmes (de DeMorgan) de l'algèbre booléenne :

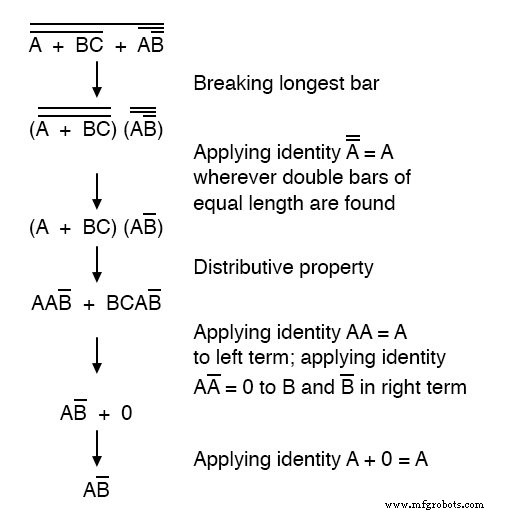
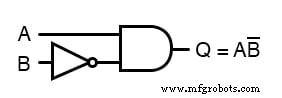
Le circuit de porte équivalent pour cette expression très simplifiée est le suivant :

AVIS :

• Les théorèmes de DeMorgan décrivent l'équivalence entre les portes à entrées inversées et les portes à sorties inversées. En termes simples, une porte NAND est équivalente à une porte OU négatif, et une porte NOR est équivalente à une porte ET négatif.
• Lorsque vous « cassez » une barre de complémentation dans une expression booléenne, l'opération directement sous la coupure (addition ou multiplication) s'inverse et les morceaux de barre brisés restent sur les termes respectifs.
• Il est souvent plus facile d'aborder un problème en cassant la barre la plus longue (la plus haute) avant de casser les barres en dessous. Vous ne devez jamais essayez de casser deux barres en une seule étape !
• Les barres de complémentation fonctionnent comme des symboles de regroupement. Par conséquent, lorsqu'une barre est brisée, les termes en dessous doivent rester groupés. Des parenthèses peuvent être placées autour de ces termes groupés pour éviter de modifier la priorité.

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail d'algèbre booléenne