Génération plasmonique de troisième harmonique à haute efficacité avec du graphène sur un réseau de diffraction de silicium dans la région de l'infrarouge moyen

Introduction

La génération d'harmoniques est un processus optique non linéaire, dans lequel N photons de même fréquence ω interagissant avec un matériau non linéaire sont combinés pour générer de nouveaux photons de fréquence Nω . En tant que moyen d'étendre les sources de lumière cohérentes aux courtes longueurs d'onde, la génération de troisième harmonique (THG) a suscité un intérêt considérable pour la recherche. Classiquement, la génération d'harmoniques à haut rendement est réalisée dans des cristaux exotiques, mais ce qui compromet l'intégration photonique à haute densité [1]. Le silicium est devenu le matériau de choix en tant que support d'information optique pour transmettre des signaux lumineux dans des circuits photoniques hautement intégrés. Les effets optiques non linéaires, tels que la diffusion Raman stimulée [2] et THG [3,4,5], ont un grand potentiel pour élargir les fonctionnalités de la photonique sur silicium. Cependant, l'émission de lumière efficace en utilisant du silicium reste un problème difficile en raison de sa bande interdite indirecte. L'utilisation d'interactions optiques non linéaires, telles que THG, semble une approche plutôt prometteuse pour fournir une lumière cohérente pour la photonique sur silicium. En général, l'efficacité de conversion THG (CE) pour un guide d'ondes optique peut être améliorée en utilisant l'adaptation de phase entre le mode fondamental et le mode de troisième harmonique. Cette méthode nécessite généralement des configurations compliquées, qui sont généralement difficiles à mettre en œuvre dans des situations pratiques. Une méthode efficace et robuste pour améliorer le THG CE peut être élaborée en augmentant l'intensité lumineuse dans le matériau non linéaire, ce qui nous offre la possibilité de relâcher les exigences strictes pour la condition de correspondance de phase. Ceci a été récemment réalisé en utilisant des cristaux photoniques de silicium à lumière lente à facteur de qualité ultra-élevé [3,4,5], des microbâtonnets de silice à petit volume modal [6] et des plasmons de surface [7,8,9,10]. Il a été rapporté que les cristaux photoniques de silicium ont amélioré le THG CE à l'amplitude de ~ 10 ^-7 en raison de la vitesse de groupe réduite de c/40 [4]. Tout récemment, des plasmons de surface se sont avérés capables d'augmenter le CE THG de l'ordre de 10 ⁻⁵ en raison de l'amélioration du champ électrique serré [7].

Ces dernières années, la longueur d'onde de fonctionnement de la photonique sur silicium s'est étendue aux régions de l'infrarouge moyen et lointain (IR) en raison de nombreuses applications potentielles telles que la détection chimique et biologique [11]. L'utilisation de la plasmonique dans les régions de l'IR moyen et lointain est attrayante car la perte de propagation d'un guide d'ondes plasmonique diminue considérablement aux longueurs d'onde plus longues et aussi parce que la section efficace de mode de ces guides d'ondes est inférieure à la longueur d'onde, ce qui améliorerait considérablement les interactions lumière-matière telles que Conversion THG [7,8,9,10, 12, 13]. Des études récentes ont prouvé que le graphène est un excellent matériau optique non linéaire pour améliorer l'effet non linéaire, conduisant à diverses applications, notamment le mélange à quatre ondes [14, 15], le THG [16, 17, 18], la commutation tout optique [19], et la bistabilité optique [20, 21], en raison de sa grande susceptibilité optique non linéaire de troisième ordre. En particulier, le seuil observé de bistabilité optique peut être considérablement réduit, grâce à la grande susceptibilité optique non linéaire de troisième ordre du graphène [20, 21]. Plus intéressant encore, contrairement au mode plasmon dans les métaux, les plasmons de graphène (GP) ont des vecteurs d'onde significativement plus grands ainsi qu'un confinement de la lumière beaucoup plus élevé, ce qui indique la capacité d'améliorer encore le CE du THG [13]. Cependant, un couplage direct entre les GP à fréquence fondamentale (FF) et les ondes de rayonnement est empêché en raison de leur décalage de quantité de mouvement, ce qui rend la mise en œuvre de ce schéma difficile dans la pratique. C'est pour cette raison que les chercheurs ont utilisé la résonance en mode guidé des réseaux pour résoudre le problème du couplage [12, 18, 20]. Le schéma proposé dans la Réf. [18] est spécialement conçu pour exciter directement les GPs FF et donc améliorer le CE des ondes en espace libre de la troisième fréquence harmonique (THF) dans le domaine térahertz.

Dans cet article, nous avons également utilisé la résonance en mode guidé des réseaux pour exciter efficacement les GP FF sur les feuilles de graphène. Différent de la configuration de la Réf. [18] où les GP sont utilisés pour améliorer le CE des ondes d'espace libre THF dans le domaine térahertz, ici, les GP sont utilisés pour générer des GP THF à des fréquences infrarouges sur une puce de silicium. L'intensité du champ géant des GPs FF en combinaison avec une grande susceptibilité non linéaire de troisième ordre du graphène entraîne un CE sensiblement amélioré des GPs THF sur la feuille de graphène dans les régions IR moyen et lointain. Nous notons une étude précédente sur l'utilisation de conditions de quasi-appariement de phase pour améliorer l'EC des GPs THF sur une surface de graphène [13]. Cependant, nous soulignons ici, bien qu'un CE élevé entre FF et THF GP soit réalisable dans la réf. [13], il manque un couplage direct entre les ondes radiatives et les GP. En revanche, le schéma présenté peut non seulement être couplé directement avec les ondes spatiales FF, mais peut également générer de manière très efficace les GPs THF, ce qui rend la proposition adaptée à l'intégration sur une plate-forme photonique en silicium. De plus, les convertisseurs de fréquence plasmoniques démontrés présentent les avantages d'une compacité et d'un CE élevé, tout en nécessitant une faible puissance incidente [22, 23].

Méthodes

La conductivité de surface du graphène peut être estimée par la formule Kubo largement utilisée sous l'hypothèse d'un potentiel chimique (également appelé énergie de Fermi), μ _c . Dans les fréquences infrarouges et térahertz, avec |μ _c | k _B T (k _B est la constante de Boltzmann, et T est la température), la conductivité de surface du graphène pourrait être approchée comme

où e est la charge électronique, est la constante de Planck réduite, ω est la fréquence radian, et τ est le temps de relaxation de la quantité de mouvement représentant le mécanisme de perte. Dans notre étude, la température de travail est supposée être T = 300 K. En prenant la feuille de graphène individuelle comme une monocouche sans interaction, la conductivité optique du graphène à quelques couches est nσ _g [24], où n est le nombre de couches de graphène (n < 6). Nous modélisons le graphène comme un matériau anisotrope et la permittivité effective dans le plan peut être écrite sous la forme [25, 26].

où η ₀ (=377 Ω) est l'impédance de l'air, k ₀ est le vecteur d'onde dans l'air, et d _g est l'épaisseur totale de n -feuilles de graphène en couches. La permittivité hors plan du graphène, ε _y , est maintenu constant à 2,5, quel que soit le niveau de Fermi [27, 28].

Résultats et discussion

Excitation des GPs FF avec un réseau de silicium

Tout d'abord, nous considérons l'excitation des GPs FF et la génération des GPs THF sur des feuilles de graphène soutenues par un réseau diélectrique (GSSDG) comme le montre la Fig. 1. Considérant la situation pratique selon laquelle la zone de graphène peut être des centaines de fois plus grande que la section du réseau, on suppose que les feuilles de graphène sont plates sur le dessus des réseaux et ne sont pas conformes aux réseaux. Nous avons noté certaines études de recherche sur la GP supportée par des feuilles de graphène soutenues par des réseaux où les feuilles de graphène sont supposées plates [12, 13]. En particulier, nous trouvons que les résultats expérimentaux sont bien cohérents avec les résultats de la simulation, où les feuilles de graphène sont supposées être plates dans la modélisation [12]. Le GSSDG est supposé infini le long de x direction et périodique le long de z direction. L'épaisseur de la couche de réseau de silicium sous les feuilles de graphène est supposée être de 2 µm. Dans ce cas, la couche de réseau peut être considérée comme infiniment épaisse dans la modélisation puisque le substrat de silicium sous le réseau n'affecte pas la distribution de champ des GP dans le modèle de réseau air-graphene. La relation dispersive des GP pris en charge par cette configuration peut être exprimée par [29].

où β est la constante de propagation des GP le long de z- axe, ε ₀ est la permittivité dans l'air, et ε _{r 1} (=1) et ε _{r 2} sont les constantes diélectriques des milieux diélectriques au-dessus et au-dessous des couches de graphène, respectivement. Comme la période du réseau est beaucoup plus petite que la longueur d'onde de la lumière dans l'air, le réseau de silicium peut être approximativement modélisé comme un milieu efficace avec la permittivité équivalente [30].

où ε _silicium (=11.9) est la permittivité du silicium aux fréquences infrarouge et térahertz [31], et f (=w /p ) est le taux de remplissage du silicium (f est fixé à 0,5 dans ce travail).

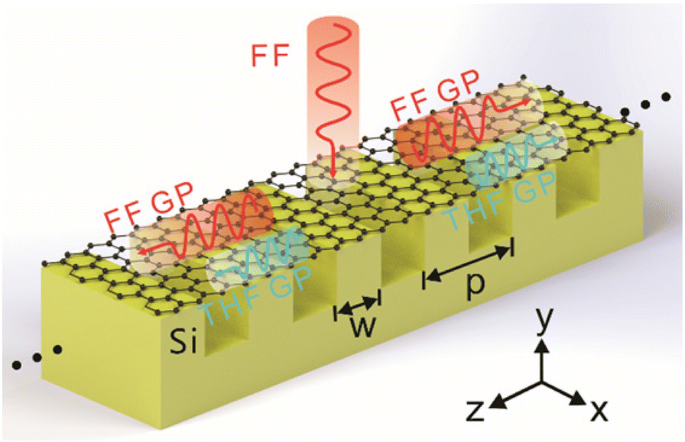
Le schéma du GSSDG en tant que convertisseur de longueur d'onde THG. Les GPs FF (courbes rouges) sont excités avec une onde plane polarisée en x à incidence normale de FF, puis génèrent les GPs THF (courbes bleues) en raison des réseaux de silicium sous les feuilles de graphène. La période de la grille est p , et w désigne la largeur du silicium

La relation de dispersion des GP sur le GSSDG pour différents paramètres (τ , μ _c , etd _g ) est illustré à la Fig. 2. Dans l'ensemble du travail, un domaine temporel aux différences finies (FDTD) bidimensionnel avec un logiciel commercial de Lumerical FDTD Solution est réalisé pour effectuer la modélisation numérique. Dans la simulation de cette partie, les limites de couche parfaitement appariées et les limites périodiques sont utilisées dans le y et z directions, respectivement, tandis que la structure entière est supposée infinie le long du x direction. Les tailles de maille avec 0,1 nm le long de y direction et 10 nm le long de z direction sont utilisés pour décrire le graphène, tandis que des maillages non uniformes avec une valeur maximale de 20 nm le long de y direction et maille uniforme de 10 nm le long de z direction sont adoptées dans les régions autres que les feuilles de graphène. On peut voir sur les Fig. 2a, d, g que, dans la gamme de longueurs d'onde considérée, le vecteur d'onde des GPs est des dizaines de fois plus grand que celui de l'air, ce qui indique que le champ optique des GPs est fortement confiné sur le surface de graphène. Cependant, le décalage de phase entre les GPs et les ondes de rayonnement empêche le couplage direct entre eux. Le réseau de diffraction au silicium sous les feuilles de graphène illustrées sur la figure 1 peut fournir une impulsion supplémentaire pour surmonter la différence de vecteur d'onde afin que les GP FF puissent être excités efficacement avec une incidence d'onde plane. La période de râpage, p , doit répondre à l'équation de correspondance de phase comme

où β _FF est la constante de propagation des GP FF le long de z -axe, j est l'ordre de diffraction, et θ est l'angle incident. Pour exciter les GP FF de longueur d'onde effective de λ _FF avec l'ordre de diffraction fondamental j = 1 sous la condition d'incidence normale θ = 0, l'expression suivante doit être satisfaite

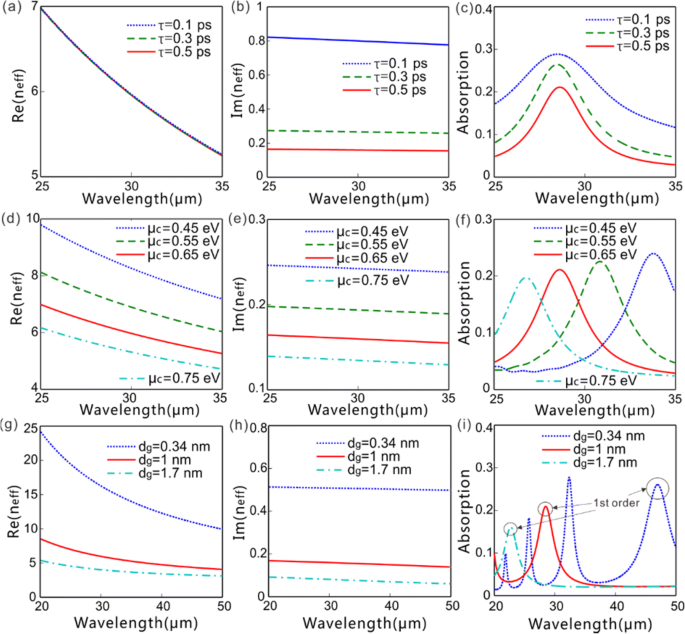
Le vrai [Re(n _eff )] et imaginaire [Im(n _eff )] parties de l'indice effectif et absorption en fonction de la longueur d'onde avec différentes valeurs de μ _c , τ , et d _g . un –c Re(n _eff ), je suis(n _eff ), et l'absorption en fonction de la longueur d'onde (τ =0,1, 0,3 et 0,5 ps, associé à μ = 0,14, 0,42, 0,69 m ² V ⁻¹ s ⁻¹ , respectivement) avec μ _c = 0.65 eV et d _g = 1 nm. d –f Re(n _eff ), je suis(n _eff ) et l'absorption en fonction de la longueur d'onde (μ _c =0,45, 0,55, 0,65 et 0,75 eV) avec τ = 0,5 ps et d _g =1 nm. g –je Re(n _eff ), je suis(n _eff ), et l'absorption en fonction de la longueur d'onde [d _g =0.34 nm (n = 1), 1 nm (n = 3), et 1,7 nm (n = 5)] avec μ _c = 0.65 eV et τ = 0,5 ps. Pour tous les cas, la période de rattrapage est fixée à p = 4 m

La figure 2 présente la dépendance du réel [Re(n _eff )] et imaginaire [Im(n _eff )] partie des indices effectifs et d'absorption sur la longueur d'onde de la lumière avec différentes valeurs de τ , μ _c , etd _g . Cela explique apparemment comment les paramètres du graphène influencent les GP FF excités sous l'illumination d'une onde plane polarisée en x à incidence normale de FF, où la période de réseau est fixée à 4 m. Tant le vrai [Re(n _eff )] et des parties imaginaires [Im(n _eff )] des indices de réfraction effectifs des GP FF diminue avec l'augmentation de la longueur d'onde de la lumière dans la plage de longueurs d'onde considérée (Fig. 2a, b, d, e, g, h). Cela signifie qu'avec une longueur d'onde de lumière plus courte, les GP sont plus fortement confinés autour des feuilles de graphène, ce qui entraîne une constante de propagation plus grande et une perte de propagation plus élevée. L'absorption est très sensible à la longueur d'onde et augmente fortement à mesure que la longueur d'onde incidente se rapproche de la longueur d'onde de résonance (Fig. 2c, f, i). Le temps de diffusion du porteur τ détermine la mobilité du transporteur μ dans le graphène comme \( \tau ={\mu \mu}_c/e{\nu}_F^2 \) avec la vitesse de Fermi de ν _F = 9,5 × 10 ⁴ Mme. Considérant qu'une mobilité de transporteur de μ> 10 m ² V ⁻¹ s ⁻¹ a été réalisé expérimentalement dans du graphène en suspension de haute qualité [32], ce qui conduit à τ> 1.5 ps, notre réglage de τ ≤ 0,5 ps peut refléter la perte de transport pratique du graphène de manière conservatrice. Le τ , associé à la mobilité du transporteur μ , influence doucement le Re(n _eff ) et la longueur d'onde d'excitation des GPs FF, mais affecte grandement le Im(n _eff ) et l'absorption (Fig. 2a–c). Le μ amélioré _c diminue Re(n _eff ) et Im(n _eff ) simultanément, réduit donc la longueur d'onde de résonance des GPs FF en conséquence (Fig. 2d-f). Le Ré(n _eff ), je suis(n _eff ), et la longueur d'onde de résonance des GP FF diminue avec l'augmentation de l'épaisseur de graphène, correspondant au nombre de couches de graphène (Fig. 2g–i).

Dans ce qui suit, nous prenons τ = 0,5 ps, μ _c = 0.65 eV, et d _g = 1 nm à titre d'exemples. La relation de dispersion des GP sur le GSSDG est illustrée à la figure 3a, où les courbes de dispersion calculées sont bien en accord avec les résultats de simulation obtenus par le logiciel commercial Lumerical FDTD Solutions. La figure 3b montre la réponse optique des feuilles de graphène avec et sans le réseau de silicium. On peut clairement voir que l'efficacité d'absorption (plus de 20%) est significativement améliorée à λ = 28,62 m lorsqu'il s'agit du réseau (p = 4 µm). En revanche, l'efficacité d'absorption est maintenue à un niveau faible (inférieur à 2%) sur toute la gamme spectrale considérée si le réseau n'est pas pris en compte. L'absorption sensiblement améliorée pour le premier cas peut être attribuée à l'excitation des GP à λ = 28,62 µm. Nous pouvons trouver du |E | distributions à λ = 28,62 m (Fig. 3c) que le GPs excité est le mode fondamental de résonance à ondes guidées (j = 1). On peut voir sur la figure 3d que la longueur d'onde de résonance du mode fondamental par rapport à la période de réseau des simulations numériques, est bien en accord avec le résultat théorique prédit par l'Eq. (6).

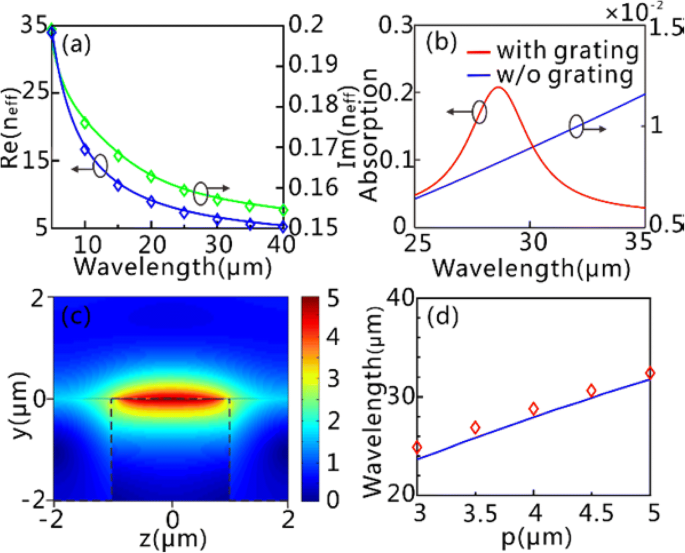
FF GPs et enrichissement du terrain sur le GSSDG. un Courbes de dispersion des généralistes sur le GSSDG. Les traits pleins bleus et verts correspondent au réel [Re(n _eff )] et imaginaire [Im(n _eff )] partie de l'indice effectif extrait de l'Eq. (3), respectivement, tandis que les losanges bleus et verts sont obtenus à partir de simulations numériques. b Spectres d'absorption avec substrat de réseau (ligne rouge) et substrat de silicium pur sans réseau (ligne bleue). c Le |E normalisé | distributions du mode GPs fondamental à 28,62 µm. Les lignes pointillées noires délimitent la couche de silicium. d La longueur d'onde d'excitation du mode GPs fondamental en fonction de la période de réseau. La ligne bleue est extraite de l'Eq. (6), et les losanges rouges sont issus de la simulation numérique. En b et c , P est fixé à 4 m. Tous les résultats de simulation sont récupérés par le logiciel commercial Lumerical FDTD Solutions

Il convient de noter qu'un champ plasmonique considérablement amélioré sur la surface du graphène se produit en raison de la réduction significative de la vitesse de groupe des GP FF (des dizaines de fois inférieures à la vitesse de la lumière dans l'air). Le champ plasmonique subit une amélioration du champ électrique 5 fois plus élevée que les ondes planes d'éclairage, ce qui devrait générer des GP THF avec un CE significativement amélioré, en combinaison avec la grande non-linéarité optique de troisième ordre du graphène [16, 17]. La réponse non linéaire du graphène peut être décrite par le coefficient de conductivité non linéaire défini comme [17].

où la vitesse de Fermi ν _F = 9,5 × 10 ⁴ m/s.

Génération de GP THF

Nous comparons ensuite l'intensité du champ électrique des GPs THF sur la surface du graphène lorsque les feuilles de graphène sont soutenues avec et sans réseau. Les conditions aux limites dans les simulations FDTD sont les mêmes que celles utilisées dans les Fig. 2 et 3. L'intensité du champ électrique normalisé (NEFI) en fonction de la longueur d'onde est présentée sur la figure 4a, lorsque les feuilles de graphène sont éclairées par une lumière à onde continue (CW) à incidence normale avec une densité de puissance de 0,11 MW/cm ² et la longueur d'onde centrale de 28,62 µm. Ici, le NEFI est obtenu en normalisant l'intensité du champ électrique à sa valeur à 28,62 µm (FF) avec la structure de réseau. On peut observer qu'un pic apparent se produit à THF dans le spectre NEFI avec structure de réseau (GSSDG), par rapport au spectre NEFI sans réseau impliqué. Définition du CE comme \( {\int}_0^p{P}_y^{THF} dz/\left({P}^{FF}p\right) \), où \( {P}_y^{THF } \) est le y composante du vecteur poynting au THF, et P ^FF est la densité de puissance de la lumière incidente, le CE atteint jusqu'à 5,71 × 10 ⁻⁷ pour le GSSDG. On peut facilement en déduire que l'excitation des GPs FF contribue à l'amélioration du CE des GPs THF. Les distributions de champ de la partie réelle de E _y au THF illustré à la Fig. 4b valider la génération de GPs THF sur la surface de graphène.

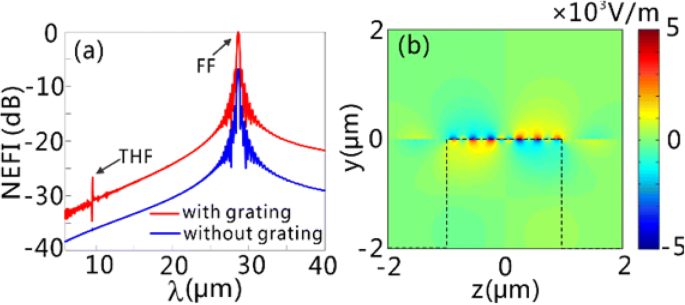
Génération de THF GPs sur le GSSDG. un Le NEFI pour la structure avec (ligne rouge) et sans (ligne bleue) réseau normalement éclairé par la lumière CW avec une densité de puissance de 0,11 MW/cm ² et la longueur d'onde centrale de 28,62 µm. Les deux pics de la ligne rouge désignent les GP FF (λ = 28.62 μm) et les GPs THF générés (λ = 9,54 μm), respectivement. b La distribution de la partie réelle de E _y pour les GPs THF générés. La ligne pointillée noire dans b représente les contours de la couche de silicium. Les paramètres structurels du GSSDG sont les mêmes que ceux de la Fig. 3

Le GSSDG comme source lumineuse pour la photonique sur silicium dans l'infrarouge moyen

Nous considérons ensuite l'utilisation du convertisseur de longueur d'onde plasmonique GSSDG pour fournir directement une source de lumière pour les circuits photoniques intégrés au silicium. À titre d'exemple illustré sur la figure 5a, deux guides d'ondes plasmon graphène-silicium (GSPW) sont attachés au GSSDG des deux côtés. Les GSPW sont choisis de telle sorte qu'ils soient capables de guider les GP sur une large bande spectrale couvrant les GP FF et THF. Puisque les distributions modales de champ des modes GP FF et THF dans le GSSDG (par rapport asymétrique à la surface du graphène) présentent une forte similitude avec les modes GP supportés sur le GSPW, on peut donc en déduire qu'une fois la section du réseau éclairée avec une incidence normale Les ondes FF, les GP FF et THF générés au-dessus de la région de réseau peuvent être efficacement couplés aux GSPW des deux côtés. Nous avons effectué des simulations FDTD pour valider notre prédiction. Les limites de couche parfaitement adaptées sont utilisées à la fois dans y et z orientations dans la modélisation. Nous avons simulé une onde lumineuse FF à incidence normale qui frappe la section du réseau et montré les distributions de champ électrique pour les GPs FF et THF (Fig. 5b, c). Une source lumineuse à champ total/champ diffusé est utilisée pour garantir que seule la section du réseau est éclairée par la lumière incidente dans la simulation [33]. Une limite absorbante parfaitement adaptée a été utilisée pour absorber totalement toutes les ondes lumineuses qui atteignent la limite de la région de calcul. La figure 5b montre que les GP FF sont excités sur la surface de graphène au-dessus du réseau, puis se propagent le long des GSPW des deux côtés. À partir de la figure 5c, nous pouvons en outre trouver l'apparence des GPs THF sur la surface du graphène, à la fois dans la section de réseau et dans les GSPW. Ici, le CE est défini comme

où \( {P}_z^{\mathrm{THF}} \) est le z -composant du vecteur poynting au THF, \( \int {P}_z^{\mathrm{THF}}\mathrm{dz} \) est la densité de puissance de sortie du THF GP dans le GSPW, P ^FF est la densité de puissance des ondes lumineuses FF incidentes, et N _p est le nombre de période de râpage. On peut voir sur la figure 5d que le CE de THG atteint la valeur maximale de 3,68 × 10 ⁻⁷ (− 64,3 dB) à la limite du réseau et s'atténue de manière exponentielle le long de la direction de propagation en raison de la perte d'absorption ohmique du graphène.

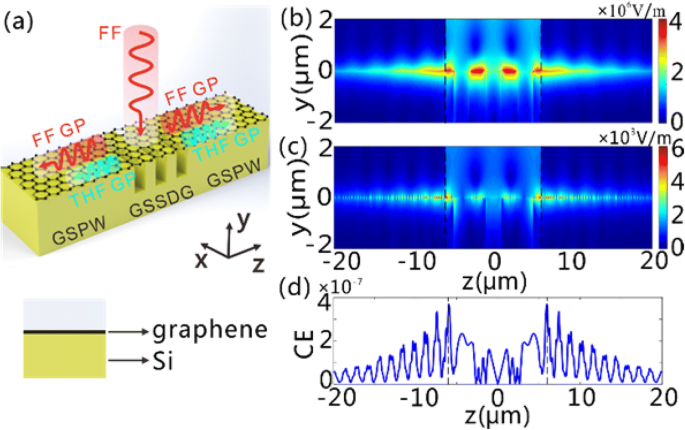
Génération de GPs FF et THF sur le GSSDG et les GSPW connectés. un Les schémas du GSSDG et des GSPW connectés des deux côtés lorsqu'une onde plane polarisée en x à incidence normale de FF illumine la structure. Les GPs THF sont générés et guidés le long des deux GSPW après que les GPs FF soient excités dans le GSSDG. La section transversale du GSPW est présentée dans le panneau ci-dessous, dans lequel les feuilles de graphène et la couche de Si sont indiquées. b , c Le |E | distributions de b FF et c THF généralistes dans le y -z plan car la section du réseau est éclairée par une lumière CW avec une densité de puissance de 0,19 MW/cm ² à 28,62 µm. d Le CE de THG le long du z direction. Les lignes pointillées noires dans b –d représentent les interfaces entre le GSSDG et les GSPW. En b –d , N _p est fixé à trois

Il est important de discuter des facteurs qui affectent le THG CE, qui est essentiel pour évaluer les performances de l'appareil d'un convertisseur de longueur d'onde THG. Pour un procédé THG, on s'attend toujours à obtenir le plus grand CE avec une puissance de pompage relativement faible. Des études antérieures ont démontré que l'augmentation de l'intensité du champ local dans les matériaux non linéaires du troisième ordre entraîne une amélioration remarquable de l'EC du THG avec une puissance de pompe considérablement réduite [3, 4, 7]. La figure 6a montre l'influence de la densité de puissance des ondes lumineuses incidentes sur le CE maximal dans les GSPW, qui augmente avec la densité de puissance. Notez que le CE maximum atteint jusqu'à 3,68 × 10 ⁻⁷ même si la densité de puissance des ondes lumineuses incidentes est aussi faible que 0,19 MW/cm ² , qui est de 6 à 7 ordres de grandeur plus petit que ceux de la même bande spectrale [22, 23]. Nous montrons sur la figure 6b que le nombre de période de réseau utilisé, N _p , affecte également le CE dans les GSPW. Lorsque N _p est augmentée, une partie réductrice des GP THF générés au centre du réseau atteint les GSPW en raison de la perte de propagation accrue induite par l'absorption du graphène. Néanmoins, la puissance d'entrée, associée à N _p , présente une amélioration linéaire. Par conséquent, le CE maximum des GPs THF diminue avec l'augmentation de N _p . Nous soulignons ici que la densité de puissance de sortie absolue des GPs THF devrait être plus significative pour guider la conception d'un convertisseur de longueur d'onde THG pour des applications pratiques, une fois la densité de puissance incidente fixée. Bien que le CE maximum des GPs THF se situe à N _p = 2 dans notre cas, la densité de puissance de sortie de THG se rapproche du maximum lorsque N _p ≥ 3 (Fig. 6b). Par conséquent, nous avons utilisé 3 périodes de réseau pour la démonstration de la génération de GPs THF dans les GSPW. Pour une future mise en œuvre expérimentale avec la conception actuelle, la zone de la source FF d'entrée dépasse la région de réseau et est maintenue constante lors de la génération de THF GP avec différents numéros de réseau. Dans ce cas, le CE doit être écrit comme

où la zone de la source FF, S , est constant. Ainsi, la densité de puissance de sortie sera proportionnelle à la CE, et par conséquent, il faut sélectionner correctement le nombre de réseau optimal pour maximiser la densité de puissance de sortie du THF GP.

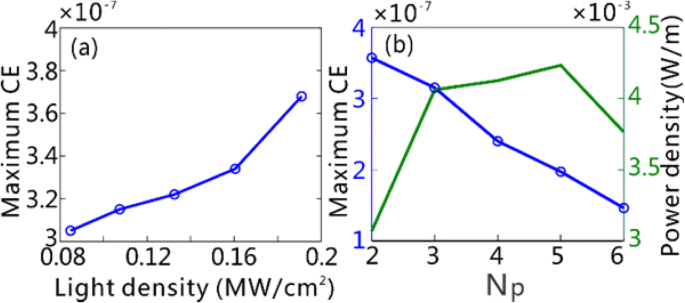
un Le CE maximum de THG en fonction de la densité de puissance incidente pour N _p = 3. b Le CE maximum et la densité de puissance de sortie maximum de THG en fonction du nombre de périodes de réseau N _p utilisé, respectivement. La densité de puissance incidente est fixée à 0,11 MW/cm ²

Les caractéristiques physiques du graphène peuvent également affecter les performances de l'appareil des GP THF une fois que la structure étudiée illustrée à la figure 5a est prête. L'énergie Fermi, μ _c , et le nombre de couches de graphène modifiera considérablement la longueur d'onde de résonance des GPs FF (Fig. 2f, i) et affectera donc également la longueur d'onde de génération des GPs THF. En revanche, le τ , associé à la mobilité du transporteur μ , influence à peine la longueur d'onde de résonance des GPs FF ainsi que la longueur d'onde de génération des GPs THF (Fig. 2c). Cependant, la perte de propagation des GP FF et des GP THF peut être réduite par l'utilisation d'un τ beaucoup plus grand (Fig. 2b), ce qui augmente ainsi notablement le CE des GPs THF. Considérant qu'une mobilité de transporteur de μ> 10 m ² V ⁻¹ s ⁻¹ (τ> 1,5 ps) est réalisable dans l'expérience [32], nos résultats de simulation (τ = 0,5 ps) illustré dans les (Fig. 3, 4, 5 et 6) peut présenter de manière conservatrice les performances de l'appareil du générateur THF GP de la Fig. 5a.

Enfin, il convient de discuter des influences de la rugosité de surface des feuilles de graphène sur les performances de l'appareil. La rugosité de surface du graphène pourrait potentiellement disperser le plasmon et, par conséquent, la perte de plasmon sera améliorée [34]. Le générateur THF GP proposé illustré sur la figure 5 peut être fabriqué sur la base de la technologie de fabrication micro/nano actuelle. On peut d'abord filer un polyméthacrylate de méthyle (PMMA) de 270 nm d'épaisseur sur le substrat de silicium. La couche de PMMA est développée avec MIKE\IPA après un processus ultérieur de lithographie par faisceau d'électrons. Après cela, une couche de Cr de 60 nm d'épaisseur est déposée sur la réserve avec la méthode de dépôt par évaporation par faisceau d'électrons. Le substrat de réseau de silicium peut être formé avec des techniques de gravure telles qu'une machine à plasma à couplage inductif. Suivi par une méthode de gravure humide, la couche de Cr résiduelle est éliminée par une méthode de gravure humide. Enfin, les feuilles de graphène sont transférées sur le réseau de silicium pour former la structure finale illustrée à la figure 5.

Conclusion

Nous avons démontré numériquement la génération des GPs THF dans une feuille de graphène sur des réseaux de silicium avec les ondes planes à incidence normale dans les régions de l'IR moyen et lointain. It was shown that THF GPs are generated and transmitted on the graphene surface, and the CE is dramatically enhanced due to the significantly increased field intensity of the excited FF GPs in combination of the large third-order nonlinear susceptibility of graphene. The generated THF GPs can be conveniently coupled to a GSPW, which greatly facilitates the integration of the graphene-based wavelength converter on a silicon platform. Our proposal can stimulate making graphene-based light sources for mid- and far-infrared photonics on a silicon platform and hence broaden the functionalities of silicon photonics, such as signal processing, spectroscopy, and sensing.

Abréviations

CE:

Conversion efficiency

CW:

Continuous wave

FDTD :

Domaine temporel de différence finie

FF :

Fundamental frequency

GP:

Graphene plasmon

GSPW:

Graphene-silicon plasmon waveguide

GSSDG:

Graphene sheets sustained by dielectric grating

PMMA :

Polymethyl methacrylate

THF :

Third-harmonic frequency

THG:

Third-harmonic generation