Absorbeur parfait à bande ultra-étroite et son application en tant que capteur plasmonique dans la région visible

Contexte

Ces dernières années, les métamatériaux plasmoniques basés sur la résonance plasmonique de surface localisée (LSPR) ont obtenu des progrès significatifs grâce à leurs propriétés électromagnétiques et des applications prometteuses telles que les résonateurs monopôles [1,2,3,4,5,6,7,8] , l'amélioration de la transmission lumineuse [9,10,11,12,13] et les capteurs plasmoniques [14,15,16,17,18,19,20,21]. Pour un absorbeur en métamatériau, il est avantageux d'améliorer l'absorption des ondes électromagnétiques, tandis que les pertes optiques intrinsèques des métaux doivent être soigneusement prises en compte dans la conception d'autres dispositifs. Le premier métamatériau absorbant parfait est proposé et démontré par Landy [22]. Par la suite, des absorbeurs de métamatériaux parfaits ont été développés rapidement [23,24,25,26,27,28,29,30,31], qui peuvent généralement être classés comme absorbeurs à bande étroite et absorbeurs à large bande en fonction de leurs différentes exigences d'application. Généralement, les absorbeurs à large bande peuvent être utilisés dans les récupérateurs d'énergie tandis que les absorbeurs à bande étroite sont utilisés dans les capteurs et les photodétecteurs monochromatiques.

Dans les applications de détection, le capteur d'indice de réfraction plasmonique basé sur des absorbeurs à bande étroite a attiré beaucoup d'attention. À ce jour, de nombreux types différents de capteurs à indice de réfraction plasmonique fonctionnant dans la région infrarouge et térahertz ont été signalés, notamment des microcavités hybrides [32, 33], des nanodisques [34], des métasurfaces de type réseau [24], des réseaux métalliques [28] et ainsi de suite [35,36,37]. Notez que, par rapport aux capteurs plasmoniques fonctionnant dans l'infrarouge, le térahertz et les micro-ondes, les capteurs fonctionnant dans la bande visible peuvent réaliser une périodicité plus petite de la structure du métamatériau, ce qui peut améliorer l'utilisation de ces dispositifs dans de nombreuses applications pratiques, telles que la chimie et biologie [38]. Malheureusement, les capteurs d'indice de réfraction plasmoniques publiés précédemment dans la région visible ont généralement un FOM relativement faible, ce qui entravera considérablement leur développement et leur application. Dans des études théoriques, en 2015, Zhou et al. a théoriquement proposé un capteur d'indice de réfraction dans la région visible en utilisant les structures de réseau métallique sous-longueur d'onde avec un S de 300 nm/RIU, mais le FOM n'est que de 2 [28]. Liu et al. a conçu un capteur multispectral avec des nanocavités plasmoniques à sous-longueur d'onde profonde et a démontré un FOM de 58 [34]. Avec les efforts de Liu et al., un capteur d'indice de réfraction avec un FWHM minimum atteignant 3 nm et un FOM de 68,57 a été obtenu via la structure plasmonique avec une métasurface de type réseau [24]. Dans des études expérimentales, en 2014, Emiko et Tetsu ont démontré expérimentalement un capteur LSPR basé sur une structure nanostar unique Au avec un S de 665 nm/RIU et une FWHM allant jusqu'à 40 nm [39]. Cho et al. ont rapporté une démonstration expérimentale d'un capteur d'indice de réfraction plasmonique avec le S atteignant 378 nm/RIU [40]. Tant en théorie qu'en expérience, de nombreux chercheurs ont fait de gros efforts pour améliorer le FOM du capteur d'indice de réfraction fonctionnant dans la région visible. Cependant, la conception d'un capteur à indice de réfraction plasmonique avec un FOM élevé dans la région visible reste un grand défi, ce qui limite considérablement ses applications.

Pour les capteurs, il est très significatif d'augmenter le FOM. Par exemple, dans le domaine biologique, un FOM plus élevé du capteur d'indice de réfraction signifie une performance plus élevée dans la détection de molécules. Le FOM du capteur dans ce travail peut atteindre 233,5, ce qui est bien supérieur à celui du capteur d'indice de réfraction plasmonique publié dans la région visible [24, 28, 34]. Le capteur plasmonique est basé sur la structure périodique métal-diélectrique-métal (MDM). Ensuite, la structure peut également fonctionner comme un parfait absorbeur plasmonique à bande ultra-étroite avec une efficacité d'absorption de plus de 95 % et une FWHM de seulement 1,82 nm dans la région visible. Nous étudions également les influences des dimensions de la structure et des paramètres du matériau sur les propriétés optiques du métamatériau. De plus, nous démontrons que, par rapport aux structures MDM courantes, l'utilisation de nanorubans triangulaires dans la structure est utile pour améliorer les performances d'absorption. Et pendant ce temps, les mécanismes d'absorption sont également étudiés et analysés en détail. Compte tenu de la fabrication de la structure proposée, les nanorubans triangulaires peuvent être fabriqués par de nombreuses méthodes, telles que la lithographie par faisceau électronique [41], le moulage [42] et la lithographie par impression [43]. Il est prévu que notre travail servira de guide pour la conception d'un capteur plasmonique.

Méthodes

La figure 1 illustre la section transversale d'une cellule unitaire pour la structure de métamatériau proposée. La structure se compose de deux réseaux de nanorubans d'or sur une fine couche d'or prise en sandwich entre la couche diélectrique et le substrat, et il y a un nanoruban d'or triangulaire entre les nanorubans d'or. Dans notre simulation, la permittivité de l'or est caractérisée par le modèle de Drude. Le diélectrique de la couche intermédiaire et du substrat sont réglés en NaF (n = 1.3) et MgF₂ (n = 1.4), respectivement. Nous utilisons la méthode bidimensionnelle du domaine temporel aux différences finies (FDTD) pour calculer la transmission et la réflexion de la structure proposée et l'absorption de la structure entière est définie comme A = 1 − R − T. Nous définissons des conditions aux limites de période dans la direction x, et l'onde magnétique transversale (TM) est incidente normalement sur la structure avec une polarisation le long de la direction x.

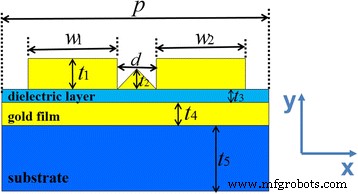
Schéma de la structure métamatérielle proposée d'une maille élémentaire

Comme nous le savons tous, le modèle de circuit LC équivalent est largement utilisé pour prédire qualitativement la résonance magnétique excitée par LSPR pour un absorbeur parfait [44,45,46]. Pour la commodité de la discussion sur le modèle LC, le schéma de la structure de l'absorbeur en métamatériau est représenté sur la figure 2a. Et le modèle LC équivalent est illustré à la Fig. 2b. Ici, la capacité de l'espace entre les nanorubans dans l'unité voisine peut être exprimée sous la forme C _g = ε ₀ t ₁ /(P − d − 2w ), où ε ₀ est la permittivité diélectrique du milieu environnant. La capacité C _m = c ₁ ε ₃ ε ₀ (2w + d )/t ₃ est utilisé pour représenter la capacité entre les nanorubans et le film d'or, où c ₁ est un coefficient dû à la distribution de charge non uniforme à la surface du métal et ε ₃ est la permittivité de la couche diélectrique [44,45,46]. L'inductance mutuelle des nanorubans d'or et du film d'or est donnée par L _m = 0,5μ ₀ (2w + d )t ₃ , où μ ₀ est la perméabilité du milieu environnant. Pour tenir compte de la contribution des charges dérivantes dans les nanorubans d'or et le film d'or, l'inductance cinétique est donnée par \( {L}_e=\left(2 w+ d\right)/\left(\gamma {\varepsilon} _0{t}_1{\omega}_p^2\right) \), où γ est un coefficient représentant la section efficace des nanorubans d'or et ω _p est la fréquence plasma de l'or [44,45,46]. Ensuite, l'impédance totale pour le modèle de circuit LC équivalent peut être exprimée sous la forme

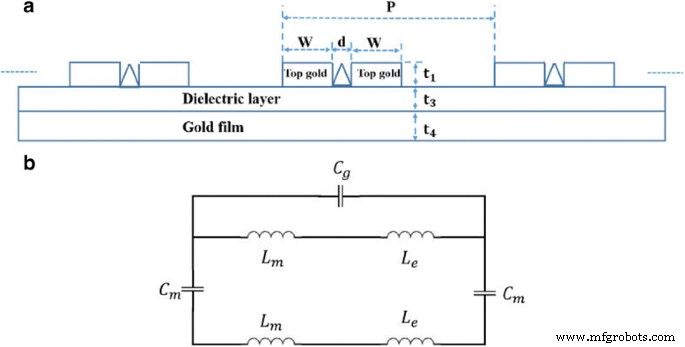
un Schéma de la structure de l'absorbeur en métamatériau. b Schéma du modèle de circuit LC équivalent pour la structure de la Fig. 6a

La longueur d'onde de résonance peut être obtenue lorsque Z _tpas = 0.

Le couplage entre les nanorubans en unité voisine est très faible en raison du grand gap (P − d − 2w ) entre les nanorubans. L'influence de C _g peut être ignoré lorsque C _g est inférieur à 5 % de C _m . Ainsi, dans cette situation, la longueur d'onde de résonance peut être simplifiée à

où L _m = 0,5μ ₀ (2w + d )t ₃ , \( {L}_e=\left(2 w+ d\right)/\left(\gamma {\varepsilon}_0{t}_1{\omega}_p^2\right) \), et C _m = c ₁ ε ₃ ε ₀ (2w + d )/t ₃ . Dans le modèle de circuit LC, les influences des dimensions structurelles sur la longueur d'onde de résonance peuvent être prédites qualitativement par l'équation. (3). Il est facile d'observer que la longueur d'onde de résonance λ _r augmenterait avec une permittivité plus grande (ε ₃ ) de la couche diélectrique, du fait de l'augmentation de C _m . De même, la plus grande largeur w entraînera les valeurs les plus élevées pour L _m , L _e , et C _m , entraînant un décalage vers le rouge de la longueur d'onde de résonance. L'augmentation de la permittivité (ε ₀ ) de l'environnement environnant se traduira par un plus grand L _m C _m valeurs, tandis que l'autre terme L _e C _m est indépendant du ε ₀ dans l'éq. (3). Ainsi, la longueur d'onde de résonance augmentera avec l'augmentation de ε ₀ .

Résultats et discussion

Ensuite, nous commençons la discussion avec les dimensions de structure suivantes. La structure a une période de réseau de P = 580 nm dans la direction x. Les hauteurs du nanoruban d'or carré et du nanoruban d'or triangulaire sont respectivement définies comme t ₁ = 45 nm et t ₂ = 30 nm . Les épaisseurs de la couche diélectrique, du film d'or et du substrat sont t ₃ = 10 nm, t ₄ = 25 nm , et t ₅ = 165 nm , respectivement. La largeur du nanoruban d'or triangulaire et du nanoruban d'or carré sont d = 75 nm et w ₁ = w ₂ = w = 142nm , respectivement. La figure 3a présente les spectres d'absorption, de réflexion et de transmission simulés de la structure conçue. Comme le montre la figure 3a, l'efficacité d'absorption peut atteindre jusqu'à 95 % et le creux de réflectivité de la structure inférieur à 0,001 se trouve à 751,225 nm. Le FWHM est de 1,82 nm, ce qui est beaucoup plus étroit que celui de l'absorbeur à bande étroite signalé précédemment dans la région visible [24, 28, 34, 39].

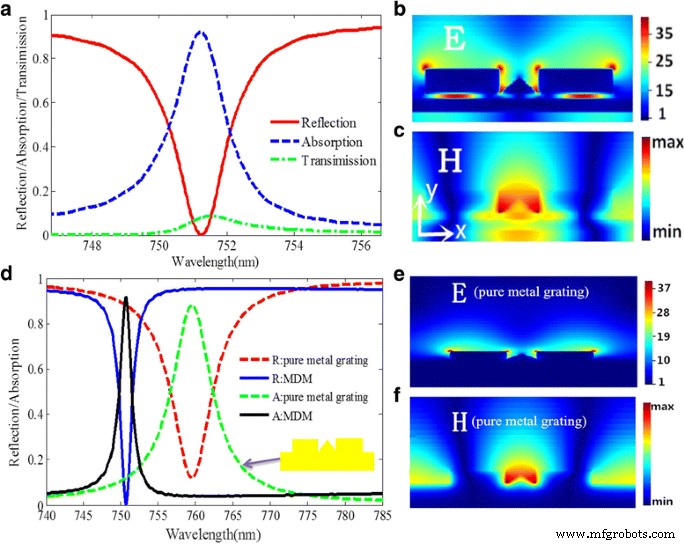
un Spectres d'absorption, de réflexion et de transmission de la structure proposée. b Distributions du champ électrique E de la structure MDM au pic de résonance. c Distributions du champ magnétique H de la structure MDM au pic de résonance. d Les spectres de réflexion et d'absorption de la structure MDM et de la structure de grille en métal pur. e Distributions du champ électrique E de la structure de grille en métal pur au pic de résonance. f Distributions du champ magnétique H de la structure de grille en métal pur au pic de résonance

Pour élaborer le mécanisme physique du pic d'absorption, les distributions du champ électrique E et du champ magnétique H au pic de résonance sont calculées et représentées sur la Fig. 3b, c. De toute évidence, comme le montre la figure 3b, l'amplitude du champ électrique dans les espaces peut atteindre une valeur jusqu'à 35 fois plus grande que la lumière incidente. Par conséquent, la structure proposée peut réaliser non seulement l'absorption parfaite mais également l'amélioration du champ électrique dans une nanofente, ce qui est un phénomène important dans les applications de biodétection. Comme le montre la figure 3c, le champ le plus magnétique est concentré dans l'espace entre deux nanorubans d'or et certains pénètrent dans la couche diélectrique, ce qui indique l'effet de couplage résultant du LSPR. Ensuite, afin de mieux comprendre l'influence de la couche diélectrique et du film d'or sur le FWHM ultra-étroit et les performances d'absorption élevées, le spectre d'absorption et de réflexion est analysé et comparé entre la structure MDM et la structure de réseau en métal pur avec le même paramètres dimensionnels, comme le montre la Fig. 3d. De toute évidence, la structure MDM a une FWHM plus étroite et une réflectivité plus faible du creux de résonance. Le champ électrique et le champ magnétique de la structure du réseau métallique sont simulés et présentés sur les Fig. 3e, f, respectivement. De toute évidence, par rapport à la distribution du champ magnétique de la structure MDM, le champ magnétique de la structure à réseau métallique n'est situé qu'à la surface du nanoruban d'or triangulaire sans le champ magnétique traversant le métal, ce qui peut être utilisé pour expliquer le résultat comparatif de l'absorption entre la structure MDM et la structure de grille métallique. De plus, en raison du comportement de couplage dans la structure, comme le montre la Fig. 3b, l'intensité du champ électrique entre deux nanorubans d'or et le film d'or mince est environ 40 fois plus grande que celle des ondes incidentes, qui est beaucoup plus grande que celle rapportée en réf. [25].

La figure 4a montre l'effet de la configuration de polarisation de la lumière incidente sur le spectre d'absorption de l'absorbeur en métamatériau proposé. On peut voir que la structure a un pic d'absorption net en configuration TM, mais pas en configuration TE. Évidemment, le LSPR ne peut pas être excité par la lumière incidente avec la configuration TE, ce qui s'explique bien par la structure asymétrique de l'absorbeur. De plus, dans un système réel, en raison de la diffusion de surface et des effets de joint de grain dans le film d'or mince, la constante d'amortissement du film d'or mince est probablement plus élevée que celle de l'or en vrac. Pour prendre en compte l'influence de la constante d'amortissement du film d'or mince, la figure 4b montre que le spectre d'absorption calculé des constantes d'amortissement du film d'or est trois et cinq fois supérieur à celui de l'or massif. Évidemment, des pics d'absorption avec différentes amplitudes et FWHM sont observés. Les résultats montrent que la perte de matériau accrue du métal est défavorable pour améliorer encore les propriétés absorbantes de l'absorbeur à bande étroite proposé, qui sont cohérents avec les recherches antérieures [17].

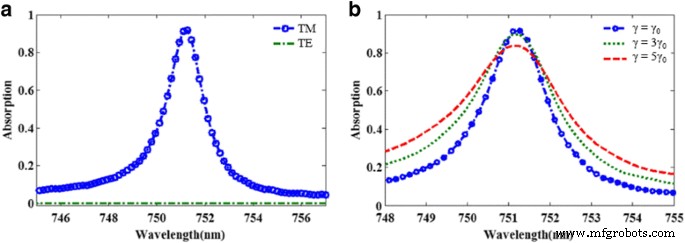
un Les spectres d'absorption de la structure proposée sous des configurations de polarisation TE et TM. b Spectres d'absorption calculés en fonction de la constante d'amortissement du film d'or

Il est généralement connu que les propriétés du métamatériau absorbant sont fortement influencées par la forme géométrique et les dimensions structurelles de la structure. Tout d'abord, nous étudions l'effet du nanoruban d'or triangulaire sur le spectre de réflectance de la structure conçue. Le nanoruban d'or triangulaire de la structure est supprimé ou transformé en un nanoruban d'or carré et semi-elliptique, respectivement, comme le montre la figure 5c-e, les autres paramètres restant inchangés dans la simulation. Les spectres de réflexion de ces trois structures sont analysés et comparés à celui de la structure d'origine, comme le montre la figure 5f–h, respectivement. Il est facile d'observer que la structure d'origine peut atteindre un FWHM plus étroit et un pendage de réflectivité inférieur à trois autres structures. Pour mieux comprendre ces résultats, comme le montre la Fig. 5i–l, la distribution du champ magnétique (H) au pic de résonance de ces quatre structures est respectivement tracée et la couleur présente l'intensité du champ magnétique. L'intensité du champ magnétique de la structure d'origine est évidemment plus forte que les trois autres structures. Cela signifie que le LSPR peut être excité plus efficacement dans la structure d'origine, ce qui se traduit par une FWHM plus étroite et une baisse de réflectivité plus faible.

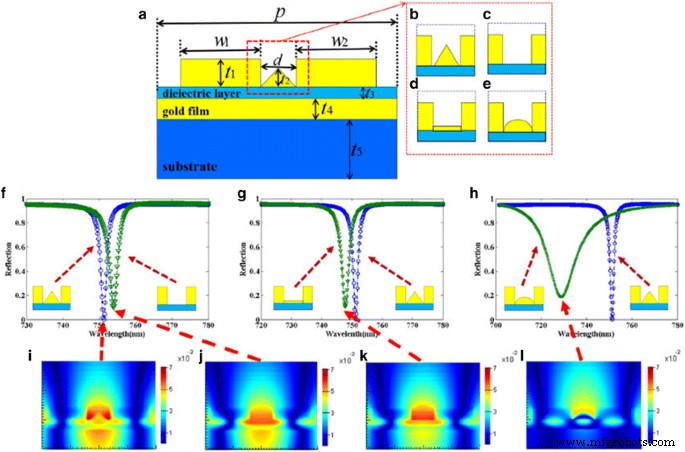
a–e Schéma du métamatériau proposé avec différentes nanostructures d'une cellule unitaire. f–h Spectres de réflexion des différentes structures. je–je Distributions du champ magnétique H au pic de résonance des structures correspondantes

D'après la figure 5, les performances optiques de la structure d'origine avec l'utilisation de nanorubans triangulaires sont supérieures à celles des autres structures. Afin de mieux comprendre les influences des nanorubans triangulaires sur les performances optiques, nous donnons un calcul et une analyse détaillés de la structure modifiée illustrée à la Fig. 6a, qui contient un nanoruban trapézoïdal avec un même angle θ au nanoruban triangulaire dans sa structure originale. Tout d'abord, comme le montre la Fig. 6b, c, nous étudions les performances optiques de la dépendance de la structure modifiée sur différentes hauteurs h du nanoruban trapézoïdal lorsque les angles θ restent inchangés. De toute évidence, lorsque la hauteur h est supérieure à 10 nm, les performances optiques de la structure resteront pratiquement inchangées, ce qui montre que les performances optiques de la structure sont robustes lors de la fabrication. Comme la hauteur h est inférieure à 5 nm, le creux de réflectivité augmente, ce qui peut s'expliquer par le fait que la hauteur h est trop petit qui abaisserait la zone effective de l'excitation de LSPR. Comme le montre la Fig. 6d, e, nous étudions également les performances optiques de la dépendance de la structure modifiée sur différents angles θ lorsque la hauteur h est définie sur 15 nm. Il est facile d'observer que les performances optiques de la structure modifiée changent peu avec la grande plage angulaire de 35° à 68°. Cependant, le creux de réflectivité augmente évidemment à l'angle θ inférieur à 30°, ce qui peut être compris que l'angle trop petit θ peut réduire l'efficacité d'excitation du LSPR. Ainsi, par l'analyse détaillée des influences des différents paramètres d'angles entre le nanoruban trapézoïdal et les nanorubans carrés sur les performances optiques, la performance d'absorption parfaite de la structure originale est attribuée à l'excitation de LSPR au coin entre le nanoruban triangulaire et les nanorubans carrés, ce qui concorde bien avec les résultats du champ magnétique illustrés à la Fig. 5i. Dans le même temps, la structure peut conserver de bonnes performances optiques dans une large gamme de hauteurs h et angles θ , ce qui suggère un grand relâchement de la robustesse de fabrication et rend la nanostructure plus réaliste d'un point de vue expérimental. Enfin, compte tenu des processus de fabrication de la nanostructure réelle, la figure 6f montre la géométrie de la structure avec la rugosité de la surface or/diélectrique et le traitement de passivation pour tous les angles vifs. La comparaison des performances optiques entre la structure modifiée et la structure d'origine est calculée et représentée sur la figure 6g. De toute évidence, l'effet de la tolérance de fabrication sur les performances de la nanostructure est très faible, ce qui montre les performances optiques robustes de la fabrication.

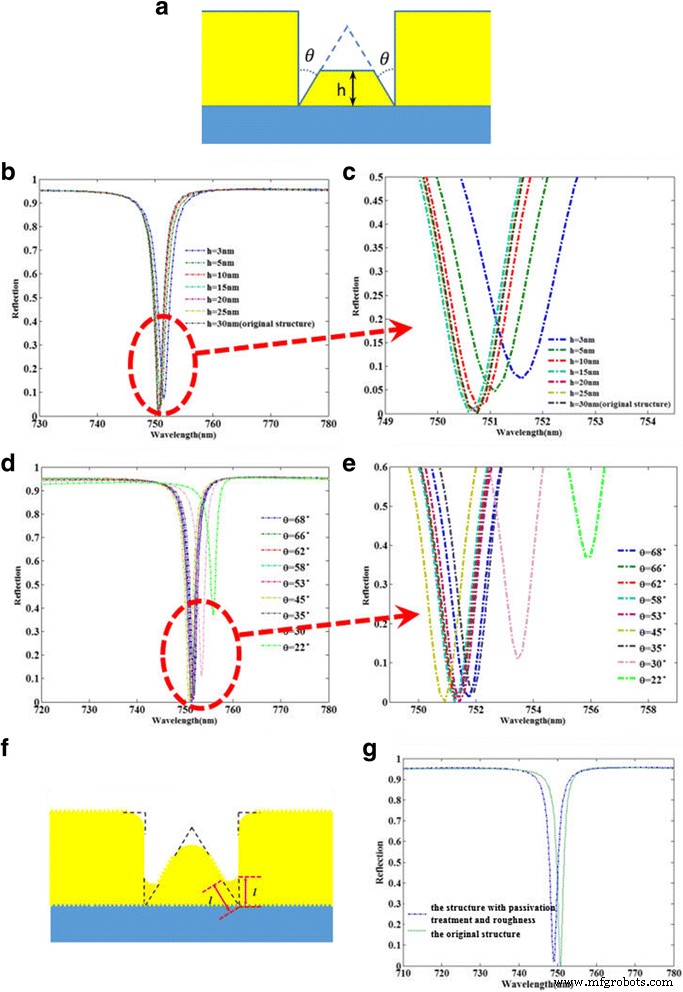
un La structure modifiée contenant un nanoruban trapézoïdal de même angle θ au nanoruban triangulaire. b , c Comparaison des spectres de réflexion entre les nanostructures de différentes hauteurs h , lorsque le θ rester inchangé. d , e Comparaison des spectres de réflexion entre les nanostructures avec des angles différents θ , lorsque la hauteur h = 15 nm. f La structure modifiée avec la rugosité de la surface or/diélectrique et le traitement de passivation pour tous les angles vifs. g Comparaison des spectres de réflexion entre la structure modifiée et la structure d'origine, lorsque le l est défini sur 3 nm

Ensuite, nous étudions également les effets de la dimension de la structure et des paramètres du matériau, en utilisant la méthode FDTD, sur la réflectivité du pendage, la FWHM et la longueur d'onde de résonance de la structure conçue. Plusieurs paramètres seront étudiés dont l'indice de réfraction du diélectrique, la largeur du nanoruban d'or w , la largeur du nanoruban d'or d , et l'épaisseur du nanoruban d'or t ₁ . La figure 7 montre l'effet de l'indice de réfraction de la couche diélectrique sur le spectre de réflectance de la structure du métamatériau. Comme le montre la figure 7a, la longueur d'onde de résonance se déplace vers le rouge évidemment avec l'augmentation de n _{diélectrique} , ce qui est cohérent avec la prédiction du modèle de circuit LC. Comme le montre la figure 5b, le creux de réflectivité est d'abord diminué puis augmenté lorsque le n _{diélectrique} est augmenté, tandis que FWHM devient plus étroit. Le FWHM et le creux de réflectivité du spectre de réflexion dépendent fortement de la force de couplage entre les nanorubans et le film d'or, ce qui entraîne des performances optiques différentes avec divers matériaux diélectriques de l'espaceur diélectrique entre les nanorubans et le film d'or. Le creux de réflectivité est la valeur minimale lorsque l'indice de réfraction de la couche diélectrique est d'environ 1,3. Dans le même temps, le FWHM est d'environ 1,85 nm, ce qui est beaucoup plus étroit que celui de l'absorbeur à bande étroite publié dans la région visible [24, 28, 34, 39].

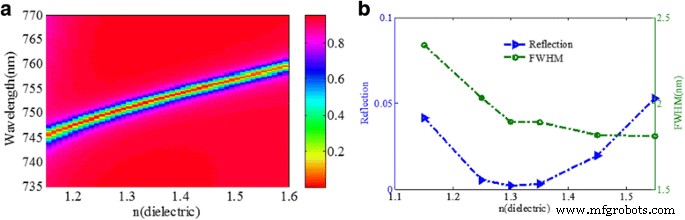
un Spectres de réflexion en fonction de l'indice de réfraction de la couche diélectrique. b Réflectivité du creux de résonance et FWHM en fonction de l'indice de réfraction de la couche diélectrique

La figure 8 présente l'influence de la largeur w du nanoruban d'or sur le spectre de réflexion de la structure métamatérielle. Comme le montre la figure 8a, lorsque la largeur du nanoruban d'or w passe de 140 à 177 nm, la longueur d'onde de résonance se déplace vers le bleu, ce qui est bien en accord avec les résultats du modèle de circuit LC équivalent. La figure 8b montre que la FWHM devient plus étroite et que le creux de réflectivité augmente avec l'augmentation de w . L'augmentation du creux de réflectivité peut résulter de l'augmentation de la surface métallique efficace pour réfléchir la lumière incidente, avec l'augmentation de w . Les valeurs minimales du creux de réflectivité et de la FWHM ne peuvent pas être obtenues simultanément. Cependant, dans notre conception, les valeurs du creux de réflectivité et du FWHM changent légèrement dans une large plage de w (140~162 nm), ce qui est favorable aux applications pratiques.

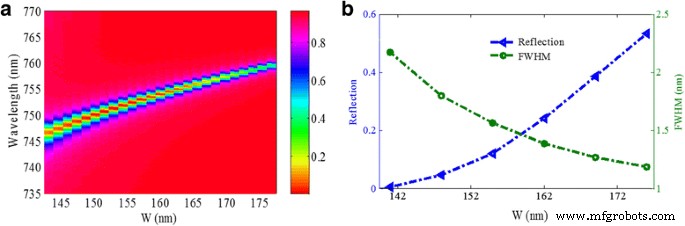
un Spectres de réflexion en fonction de la largeur w des nanorubans d'or . b Plongement de réflectivité et FWHM en fonction de la largeur w des nanorubans d'or

De plus, comme le montre la figure 9a, le creux de réflectivité peut supporter une valeur inférieure lorsque la largeur du nanoruban d'or d est compris entre 55 et 75 nm alors qu'il augmente évidemment lorsque d dépasse 76 nm, ce qui peut être expliqué qu'une distance trop grande entre les deux nanorubans peut réduire l'efficacité d'excitation pour LSPR, réduisant ainsi l'efficacité d'absorption de la lumière incidente. Le FWHM devient plus étroit avec l'augmentation de d , et la taille optimale de d est d'environ 75 nm. D'après la figure 9b, le creux de réflectivité peut conserver une valeur inférieure lorsque l'épaisseur du nanoruban d'or t ₁ passe de 35 à 50 nm tandis que la FWHM devient plus étroite. Cependant, lorsque t ₁ augmente de 50 à 60 nm, le creux de réflectivité augmente évidemment. On peut comprendre le résultat comme ça, le nanoruban est trop épais ce qui augmenterait la réflexion de la lumière incidente. La figure 9c montre que la valeur minimale du creux de résonance est obtenue lorsque la hauteur d'or triangulaire t ₂ est d'environ 30 nm. Dans cette structure, le creux de réflectivité a été inférieur à 0,025 lorsque la hauteur d'or triangulaire varie de 15 à 40 nm, ce qui est bénéfique pour concevoir une structure de métamatériau en raison de ses excellentes performances de robustesse.

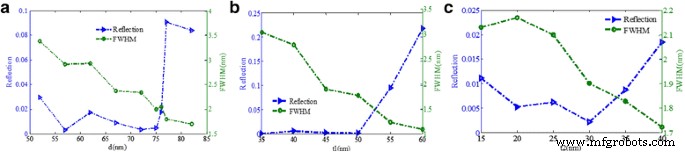
un Plongement de réflectivité et FWHM en fonction de la largeur du nanoruban d'or triangulaire d . b Plongement de réflectivité et FWHM en fonction de l'épaisseur des nanorubans d'or t ₁ . c Réflectivité du creux de résonance et FWHM en fonction de la hauteur d'or triangulaire t ₂

Il est généralement connu que la longueur d'onde de résonance de la structure du métamatériau dépend fortement de l'indice de réfraction du milieu environnemental, qui a été largement utilisé dans les applications de détection. La figure 10a montre que la longueur d'onde de résonance se déplace évidemment vers le rouge lorsque l'indice de réfraction de l'environnement augmente, ce qui est en accord avec la prédiction du modèle LC, et le creux de réflectivité peut conserver une valeur extrêmement faible en même temps. Lorsque l'IR augmente de 1,07 à 1,12, la longueur d'onde de résonance passe de 733,828 à 755,097 nm. La sensibilité de longueur d'onde calculée (S ) est d'environ 425 nm/RIU, et la FWHM peut être aussi étroite que 1,82 nm. Ainsi, le FOM peut atteindre 233,5. Pour autant que nous le sachions, le FOM est beaucoup plus élevé que celui du capteur d'indice de réfraction plasmonique précédemment publié dans la région visible [24, 28, 34, 39]. Le capteur d'indice de réfraction plasmonique proposé présente une bonne linéarité, comme le montre la figure 10b.

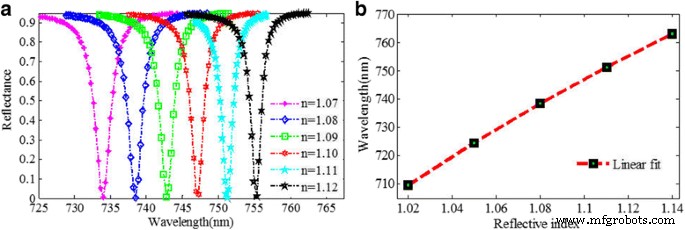
un Spectres de réflexion du capteur d'indice de réfraction plasmonique avec divers indices de réfraction de l'environnement. b Décalage de la longueur d'onde de résonance par rapport à l'indice de réfraction environnant

Dans les applications pratiques, il est généralement nécessaire de détecter le changement d'intensité relative à une longueur d'onde fixe avec les divers indices de réfraction du milieu environnant, et le facteur de mérite correspondant est défini comme FOM* = max |(dI /dn )/Je | [17]. Comme le montre la Fig. 11a, le FOM* change évidemment avec la diminution de w , et le maximum de FOM* peut atteindre 1,4 × 10 ⁵ au w d'environ 358 nm. La figure 11b montre que le FOM augmente avec la diminution de d et un maximum de FOM* est obtenu à d = 75 nm. Comme le montre la figure 11c, lorsque l'épaisseur du nanoruban d'or t ₁ est de 35 nm, le FOM* est maximal. De plus, la figure 11d montre également que le maximum de FOM* est obtenu lorsque la hauteur d'or triangulaire t ₂ est d'environ 30 nm. Les caractéristiques du FOM et du FOM* avec les changements des dimensions de la structure sont étudiées numériquement, ce qui peut offrir certains conseils pour concevoir un capteur plasmonique haute performance.

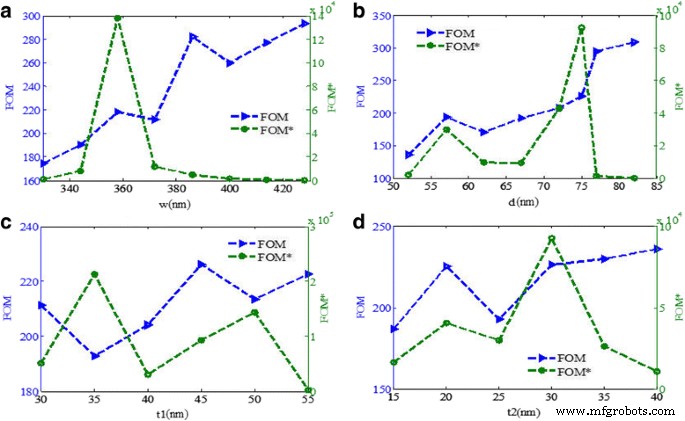
a–d FOM et FOM* en fonction de la largeur du nanoruban d'or w , la largeur du nanoruban d'or triangulaire d , l'épaisseur des nanorubans d'or t ₁ , et la hauteur d'or triangulaire t ₂ , respectivement

Conclusions

En résumé, nous proposons et démontrons numériquement un absorbeur à bande ultra-étroite presque parfait avec une absorption atteignant 95% dans la région visible. Nous effectuons en outre une analyse détaillée des influences de la forme structurelle et des dimensions structurelles sur les propriétés optiques de la structure du métamatériau en utilisant le FDTD bidimensionnel. En utilisant les dimensions optimisées de la structure, il présente le creux de réflectivité aussi bas que 0,001 avec le FWHM de 1,82 nm à incidence normale dans la région visible. De plus, nous avons également démontré sa capacité de détection. Sa sensibilité est d'environ 425 nm/RIU et le FOM peut atteindre 233,5. Ceci est bien meilleur que celui du capteur précédemment rapporté dans la région visible [24, 28, 34, 39]. Pour ses performances de détection élevées, la structure du métamatériau peut trouver des applications dans la liaison biologique, les photodétecteurs intégrés, les applications chimiques, etc.

Abréviations

FDTD :

Domaine temporel aux différences finies

FOM :

Figure de mérite

FWHM:

Full width at half maximum

LSPR:

Localized surface plasmon resonance

MDM:

Metal-dielectric-metal

S:

Sensitivity

TM:

Transverse magnetic