Spin et rotation orbitale du dimère plasmonique induite par la lumière polarisée circulaire

Contexte

La liaison optique de deux microparticules (MP) ou nanoparticules (NP) irradiées par une lumière polarisée linéairement (LP) est un comportement optomécanique important, qui est le résultat de l'interaction lumière-matière [1,2,3,4]. Il existe plusieurs distances interparticulaires d'équilibre stable entre le dimère optiquement lié ; ces distances sont presque les multiples entiers de la longueur d'onde dans le milieu [3,4,5,6]. De plus, l'orientation du dimère est perpendiculaire à la polarisation de la lumière LP. Comme la distance interparticulaire est proche de multiples entiers de la longueur d'onde, les photons diffusés entre les particules créent une interférence constructive pour induire une force de liaison. Les phénomènes de réseau optiquement lié de plusieurs MPs de silice ou Ag NPs ont également été étudiés [7,8,9,10]. Pour l'illumination d'une onde plane à polarisation circulaire (CP), Haefner et al. ont rapporté que les hélicités du spin longitudinal et de la rotation orbitale des deux nanoparticules de silice couplées d'une taille de 100 à 700 nm sont les mêmes avec la direction de la lumière incidente [11]. Récemment, Sule et al. ont trouvé expérimentalement que l'hélicité de la rotation orbitale de deux Ag NPs de rayon 75 nm liés par la force optique est opposée à l'orientation manuelle d'un faisceau CP gaussien focalisé de 790 nm dans l'eau [12] ; c'est-à-dire que le dimère d'Ag subit un couple orbital optique négatif [13, 14]. De plus, la rotation d'orbite mesurée était d'environ 4 kHz [12]. D'autre part, le spin d'un seul Au NP de rayon 100 nm induit par un faisceau gaussien CP a également été étudié [15,16,17,18]. La rotation de spin mesurée était aussi élevée que 3,5 kHz [15]. Au cours des dernières décennies, le couplage spin-orbite (SOC) longitudinal/transversal du champ optique a attiré beaucoup d'attention [19,20,21,22,23]. Par exemple, un faisceau vortex optique (p. ,31,32,33,34]. Le champ électromagnétique (EM) tordu du faisceau de vortex optique transporte à la fois le moment angulaire de spin et le moment angulaire orbital, induisant ainsi le spin longitudinal/transversal et la rotation orbitale d'un NP de sondage à proximité [18,19,20,21,22,23 ,24,25,26]. En particulier, le SOC dans le champ proche des NPs Au ou Ag est plus important en raison du mouvement collectif des électrons libres dans ces NPs (effet plasmon) [28,29,30,31].

Dans cet article, nous étudions théoriquement les comportements optomécaniques (forces et couples optiques) de deux Au NPs (dimères) couplés supportés par un substrat, qui sont induits par l'illumination d'un faisceau gaussien CP. Le substrat est nécessaire pour confiner ces NP autonomes se déplaçant dans le plan focal, au lieu de flotter dans l'espace 3D. La méthode multipolaire multiple (MMP) est utilisée pour simuler numériquement le champ EM, puis pour analyser les couples optiques orbitaux et de spin sur le dimère optiquement lié [35, 36]. A travers les réponses optomécaniques du dimère, le SOC longitudinal/transversal se manifestera. En particulier, la condition pour générer un couple orbital optique négatif sur le dimère sera également étudiée.

Méthodes

La figure 1 montre la configuration d'une paire de NP Au identiques supportées par un substrat et irradiées par une lumière CP gauche (LH) normalement incidente (onde plane ou faisceau gaussien), où d représente la distance interparticulaire. La taille du faisceau gaussien est notée w ₀ , et le plan focal est à la section transversale centrale des NPs Au. Les formulations du champ électrique de l'onde plane et du faisceau gaussien sont jointes en annexe. On suppose que l'indice de réfraction du substrat est le même que celui du milieu environnant, l'eau. Par conséquent, la lumière réfléchie ne sera pas induite à l'interface entre le milieu et le substrat; le champ optique n'est pas perturbé par l'existence du substrat [37]. D'autre part, l'existence du substrat sert de confinement pour supporter les NPs se déplaçant sur le substrat. La méthode multipolaire (MMP) est utilisée pour simuler le champ électromagnétique induit [17, 18, 35, 36]. Les forces optiques F ^j exercé sur le j e NP (j = 1, 2) sont exprimés par

Configuration d'une paire de NPs avec un substrat support, irradiées par un faisceau gaussien de taille LH CP normalement incident (w0). Les sections efficaces centrales de ces NPs sont au plan focal du faisceau gaussien, et d est la distance entre les centres des NPs. Les réponses optomécaniques sont la rotation orbitale longitudinale et le spin longitudinal/transversal

Ici, n est le vecteur normal extérieur à la surface du j e NP, et T est le tenseur de contrainte de Maxwell moyen dans le temps exprimé par

Dans l'éq. (2), Je est une matrice identité 3 × 3, la barre supérieure désigne le conjugué complexe et Re la partie réelle [17, 18, 35, 36]. Ici, ε et μ sont la permittivité et la perméabilité du milieu environnant. Notez que le E et H sont le champ total extérieur utilisé pour l'équation. (2). En fait, T est également le flux de quantité de mouvement linéaire moyenné dans le temps. Tout au long de cet article, les forces optiques sont exprimées en coordonnées cylindriques :radiale, azimutale et z - les composants de l'axe. La force radiale peut indiquer l'attraction ou la répulsion entre les deux NP et la force azimutale l'hélicité de la révolution orbitale des NP.

D'autre part, le couple de rotation optique sur le j e NP (j = 1, 2) pour la filature de NP individuel est donnée par,

Dans l'éq. (3), x ^j × T est le flux de moment cinétique et x ^j est le vecteur de position relative d'un point x à la surface S _j par rapport au centre de masse \( {\mathbf{x}}_c^j \)de j e NP ; \( {\mathbf{x}}^j=\mathbf{x}-{\mathbf{x}}_c^j \). La direction longitudinale est désignée pour être parallèle à l'axe optique (disons z direction) de la lumière incidente, et la direction transversale est perpendiculaire à l'axe optique. D'autre part, le couple orbital optique longitudinal dans le z la direction sur chaque NP, causée par la force optique azimutale, est définie comme F _θ d /2 dans les coordonnées cylindriques. La permittivité relative de Au à λ = 800 nm utilisé dans la simulation est (− 24.062, 1.507) [38].

Résultats et discussion

Nous étudions les forces optiques et les couples exercés sur deux NP Au identiques avec des rayons de 100 nm irradiés par une onde plane LH CP normalement incidente ou un faisceau gaussien focalisé au plan focal. Le milieu environnant est l'eau. La fluence de l'onde plane ou du faisceau gaussien au centre est de 25 MW/cm ² . Les centres des deux NP autonomes, soutenus par un substrat virtuel, sont autorisés à se déplacer dans le xy plan (plan focal). Les forces optiques (F _r , F _θ ) en fonction de la distance interparticulaire d pour une onde plane CP ou un faisceau gaussien focalisé avec une taille de 500 nm de λ = 800 nm sont indiqués sur les Fig. 2a, b, respectivement. La section centrale de ces NPs est au plan focal du faisceau gaussien. La figure 2a indique que pour une onde plane, il existe plusieurs distances interparticulaires d'équilibre stable avec F _r = 0 et une pente négative; le premier d ₁ est à 603 nm et le second d ₂ à 1204 nm. Ces distances interparticulaires « d'équilibre stable » sont presque les multiples entiers de la longueur d'onde dans le milieu ; c'est-à-dire, d _m =mλ /n , où n est l'indice de réfraction du milieu et m = 1, 2, 3... C'est le résultat de l'interaction lumière-matière à longue portée causée par la force de liaison optique. Cela suggère qu'il y a un ressort optique reliant les deux NP; la force de rappel F _r du ressort optique maintient les NP séparées les unes des autres à ces distances interparticulaires d'équilibre stable. Pour le cas du faisceau gaussien, les deux premières distances interparticulaires d'équilibre stable d ₁ et d ₂ sont respectivement de 585 et 1131 nm, comme le montre la Fig. 2b, légèrement plus petites que celles d'une onde plane en raison de la force de gradient induite par le faisceau gaussien.

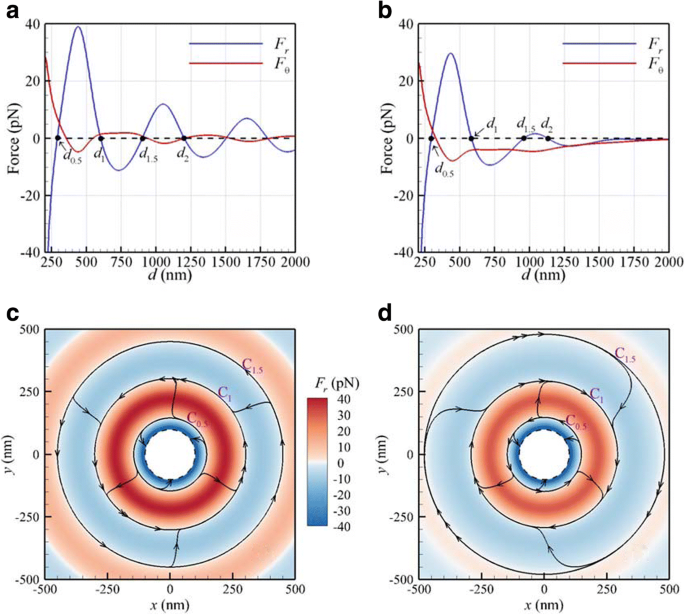
Forces optiques (F _r , F _θ ) contre d pour λ = 800 nm par CP a onde plane et b Faisceau gaussien avec une taille de 500 nm au plan focal. Les cartes aérodynamiques 2D de la force optique (F _r , F _θ ) induite par CP c onde plane et d Faisceau gaussien. La barre de couleur représente l'amplitude de F _r . L'anneau en pointillé est le cercle limite des centres de deux NPs où les NPs sont en contact

En effet, le couple orbital longitudinal F _θ d /2 conduira ces NP à tourner sur des orbites de diamètres d ₁ et d ₂ . Pour les cas avec le faisceau gaussien, les orbites seront centrées sur l'axe du faisceau. Le signe de la force optique azimutale (F _θ ) indique que la rotation orbitale longitudinale (révolution) à la première orbite d'équilibre stable induite par le faisceau gaussien est opposée à celle d'une onde plane. Cela montre que le F négatif _θ du faisceau gaussien CP génère un couple orbital négatif F _θ d ₁ /2 à la première orbite d'équilibre stable ; plus important encore, l'hélicité de la rotation orbitale du dimère Au est opposée à l'orientation manuelle de la lumière CP incidente [12]. Il est également intéressant de noter que F _θ est toujours négatif comme d> 300 nm pour les cas avec le faisceau gaussien ; le phénomène de rotation inverse (révolution) des NP optiquement liés, en raison du couple orbital négatif, est facilement observé dans les systèmes de pincettes optiques. Le couple orbital optique négatif pourrait être attribué au champ électromagnétique tordu du faisceau gaussien [23].

Selon la loi de Stokes d'une sphère mue par une force F pour se déplacer dans un fluide visqueux, la vitesse terminale v _T est v _T = F /(6πrη ), où η est la viscosité dynamique de l'eau (0,001 kg/m s). Ceci est le résultat de la force appliquée équilibrée par une force de traînée du fluide visqueux [39]. Sur la base de la loi de Stokes, le vecteur vitesse terminal d'un NP dans un milieu visqueux est proportionnel à la force appliquée [39]. Par conséquent, nous avons utilisé le champ de force optique pour obtenir les lignes de courant, qui sont presque équivalentes aux trajectoires de ces NPs. De plus, les cartes aérodynamiques 2D obtenues directement à partir du champ de vecteur de force optique (F _r , F _θ ) exercées sur les NP sont tracées sur la Fig. 2c, d pour l'onde plane et le faisceau gaussien respectivement, où la barre de couleur représente l'amplitude de F _r . Notez que la tangente de la ligne de courant en chaque point est alors parallèle au vecteur de force optique et est donc également parallèle à la vitesse de NP. Pour une petite plage de distance interparticulaire (d < d _0,5 ), la force optique radiale F _r est négatif, de sorte que ces deux NP s'attireront éventuellement pour entrer en collision, comme le montrent les Fig. 2c, d. L'anneau en pointillés est le cercle limite des centres de deux NPs où les NPs sont en contact. L'anneau interne (bleu) est une région de l'interaction à courte portée. La bague intérieure C _0,5 entre l'anneau interne (bleu, avec F négatif _r ) et le deuxième anneau (rouge, avec F positif _r ) est la frontière entre les régions d'interaction à courte et à longue portée du dimère Au ; le diamètre de C _0,5 est d _0,5 = 291 nm sur la figure 2c et d _0,5 = 296 nm sur la figure 2d. A longue distance (d _0,5 < d < d _1.5 ), les forces optiques radiales et azimutales poussent les deux NP couplées à se rapprocher de la première orbite d'équilibre stable C ₁ avec un diamètre d ₁ en raison de l'effet de la force de liaison optique. Le dimère Au optiquement lié tourne dans le sens inverse des aiguilles d'une montre (CCW) le long de l'orbite C ₁ (d ₁ = 603 nm) sur la figure 2c, tandis que le long de C ₁ (d ₁ = 585 nm) dans le sens des aiguilles d'une montre (CW) sur la Fig. 2d. La première rotation est la même que la direction manuelle de la lumière incidente causée par le couple orbital positif (F _θ > 0), et ce dernier est inversé en raison du couple orbital négatif (F _θ < 0). Selon notre analyse du spectre de section efficace de diffusion d'un dimère avec une distance d'équilibre stable de 603 nm irradié par une onde plane CP (non illustré ici), la résonance plasmonique de surface de couplage (SPR) du dimère optiquement lié est presque à 800 nm correspondant à la lumière incidente, qui est la résonance hors d'un seul NP (530 nm). En général, le couplage SPR d'un dimère dépend de la distance interparticulaire; plus la distance est grande, plus le SPR de couplage du dimère est décalé vers le rouge. Si nous utilisons un faisceau gaussien de longueur d'onde plus longue (par exemple, 1064 nm), la distance interparticulaire d'équilibre stable augmente. Cependant, à mesure que la distance entre les deux NP devient trop grande, l'effet de couplage optique diminue de sorte que le couplage SPR disparaît progressivement. Par conséquent, le SPR d'une seule NP à 530 nm devient dominant.

Pour un Au NP de rayon 100 nm qui se déplace le long d'une orbite de diamètre d et une vitesse angulaire Ω_z , la vitesse est Ω_z d /2 = F _θ /(6πrμ ). Si le faisceau gaussien est appliqué (F _θ = − 4 pN), la vitesse angulaire Ω_z (cycles par seconde) le long de C ₁ est d'environ − 7 kHz. L'ordre de grandeur est cohérent avec le résultat expérimental [12]; la vitesse angulaire de la rotation orbitale de deux Ag NPs de r = 75 nm irradié par le faisceau gaussien à 14 mW soit − 4 kHz. Si d _1.5 < d < d _2.5 , ces NP s'approcheront et tourneront le long de l'orbite secondaire d'équilibre stable C ₂ (non représenté ici). Notez que pour ces cas la force optique de F _z est négatif pour pousser ces NP vers l'aval en raison de la pression de rayonnement ; F _z = − 161,3 pN pour l'onde plane et − 117,2 pN pour le faisceau gaussien. Cela implique que la force de réaction du substrat de support est nécessaire pour équilibrer la force optique motrice de F _z . Par conséquent, les forces résultantes dans z la direction sur ces NP est nulle ; ces deux NPs sont confinés à se déplacer dans le xy plan du plan focal.

D'autre part, la Fig. 3a, b montre les couples de spin optique (M _r , M _θ , M _z ) contre d induite par une onde plane et un faisceau gaussien au plan focal, respectivement. Étant donné que les résultats de ces deux NP sont les mêmes, seul un ensemble de couples de spin optique est tracé ici. Les deux premiers (M _r , M _θ ) sont les couples de spin transverses, et ces derniers M _z est la longitudinale. On constate que l'hélicité du couple de rotation longitudinale est la même que l'orientation manuelle de la lumière incidente dans les deux cas. En effet, le moment angulaire des photons absorbés de la lumière CP incidente est transféré à ces NP pour la rotation et la rotation orbitale. Il est intéressant de souligner que les couples de spin optique transverse (M _r , M _θ ) induites par un faisceau gaussien sont significativement importantes, comparées à celles de l'onde plane. Cela pourrait être attribué aux composantes transversales du champ EM tordu au plan focal d'un faisceau gaussien. De plus, les amplitudes maximales des couples de spin transverse optiques se produisent approximativement à la première orbite d'équilibre stable C ₁ (d ₁ = 585 nm), comme le montre la figure 3b. Selon la loi de Stokes d'une sphère en rotation entraînée par un couple M dans un fluide visqueux, la vitesse angulaire terminale de la sphère est ω _T = M /(8πr ³ μ ) [18]. Par conséquent, les amplitudes des vitesses angulaires de spin longitudinal/transversal de NP à C ₁ sont d'environ 10 kHz, dont les ordres de grandeur sont en accord avec la vitesse de spin longitudinale mesurée [15], d'environ 3,5 kHz. En résumé, les phénomènes ci-dessus, comme le montrent les Fig. 2b et 3b, démontrent que la rotation orbitale longitudinale s'accompagne de spins longitudinaux/transversaux. Le mouvement des deux NP couplés est similaire à celui d'un système d'étoiles binaires, où les forces optiques fournissent les forces motrices de liaison et orbitales pour ces NP ainsi que les couples de spin optiques provoquent leur rotation.

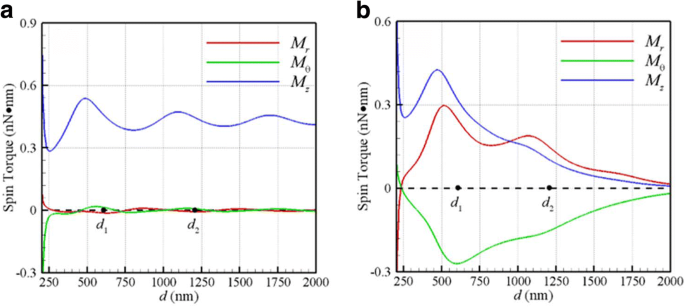
Couples de rotation optique (M _r , M _θ , M _z ) contre d à λ = 800 nm pour a onde plane et b Faisceau gaussien avec w ₀ = 500 nm au plan focal

De plus, on peut ajuster l'iris de l'objet de pinces optiques pour changer la taille du faisceau incident, modifiant ainsi l'ouverture numérique et la taille d'un faisceau gaussien. La figure 4a montre le couple orbital optique F _θ d /2 sur deux NPs Au couplées de rayon 100 nm tournant à la première orbite d'équilibre stable correspondante (d = d ₁ ) par rapport à la taille d'un faisceau CP gaussien de λ = 800 nm. La première distance d'équilibre stable correspondante d ₁ est également tracée sur la figure 4a (barre d'échelle sur le côté droit), où une onde plane peut être traitée comme un cas particulier de w ₀ → ∞. Le point de retournement pour la taille d'un faisceau gaussien entre les couples orbitaux positifs et négatifs est à 1150 nm, correspondant à F _θ = 0, comme le montre la figure 4a. Plus la taille d'un faisceau gaussien est petite, plus l'amplitude du couple orbital négatif est grande. Au fur et à mesure que la taille augmente, le d ₁ d'un faisceau gaussien approche la valeur (603 nm) d'une onde plane (w ₀ → ∞). En particulier, à mesure que la taille diminue, les amplitudes des couples de rotation transversale (M _r , M _θ ) à d ₁ augmenter considérablement, tandis que le couple de rotation longitudinal M _z diminue, comme le montre la figure 4b. Ces résultats illustrent que la taille d'un faisceau gaussien est le facteur clé pour induire un couple orbital longitudinal négatif et des couples de spin transversaux en raison du degré de distorsion du champ électromagnétique.

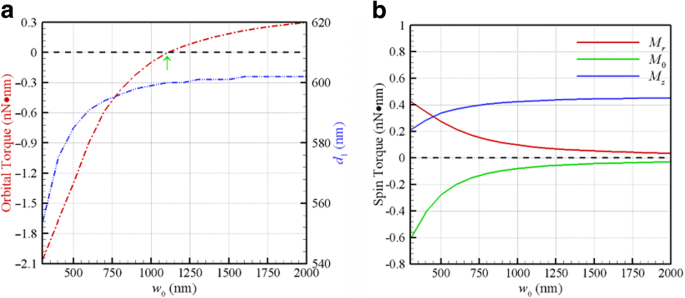
un Le couple orbital optique et d ₁ à la première orbite d'équilibre stable par rapport à la taille d'un faisceau gaussien de λ = 800 nm. Le point de retournement de la taille pour produire un couple orbital positif ou négatif est à 1150 nm. b Les couples de rotation optique par rapport à la taille à d ₁

Le mécanisme de la rotation orbitale négative et de la rotation transversale de ces NPs pourrait être attribué par la boucle du moment angulaire de spin du champ lumineux, même sans la contribution du moment angulaire orbital du faisceau lumineux [23]. Grâce aux performances du couple orbital longitudinal négatif et des couples de spin transversaux sur le dimère Au, le SOC des photons amélioré par le plasmon peut se manifester. De plus, les directions de la rotation orbitale du dimère et du spin de chaque NP dépendent de la direction de la lumière incidente.

Conclusions

Les réponses optomécaniques (forces et couples optiques) d'une paire de NPs Au irradiées par la lumière CP ont été étudiées théoriquement. Nos résultats ont montré que les orbites d'équilibre stable pour leur rotation (révolution) peuvent être induites pour l'interaction à longue distance; les distances interparticulaires d'équilibre stable sont presque les multiples entiers de la longueur d'onde dans le milieu. La force optique azimutale provoque la rotation orbitale de ces NP, et le couple de spin optique induit leur rotation, en particulier les composantes transversales. Ce mouvement est similaire à celui des étoiles binaires de masse égale se déplaçant sur une orbite circulaire autour de leur centre de masse commun. Lorsque la taille d'un faisceau gaussien est plus petite qu'un point de retournement, l'hélicité de la rotation orbitale du dimère Au optiquement lié est opposée à l'orientation manuelle de la lumière CP incidente. De plus, le SOC longitudinal/transversal devient important lorsque la taille d'un faisceau gaussien diminue ; par conséquent, le spin transversal des deux NP devient plus profond. Pour l'interaction à courte portée, la force optique provoque l'attraction mutuelle. Par conséquent, les deux NP plasmoniques couplées non seulement tournent mais tournent également avec une trajectoire en spirale et finiront par entrer en collision. De plus, la limite de la distance interparticulaire entre les interactions à longue et à courte portée de deux NP couplées est approximativement à une demi-longueur d'onde dans le milieu. Nos résultats ont démontré que l'ordre de grandeur de la force optique est d'environ pN, qui peut être comparé aux autres forces (par exemple, la force pondéromotrice) pour identifier la contribution sur le mouvement des NP. Notre découverte pourrait ouvrir la voie aux applications du SOC sur les NP manipulant la lumière pour les nanosciences et les nanotechnologies. De plus, il convient d'étudier la corrélation entre le spin optique et les couples orbitaux sur les deux NP et les densités de spin et de moment angulaire orbital du champ EM ; le premier est défini par \( \operatorname{Im}\left(\overline{\mathbf{E}}\times \mathbf{E}\right)/2\omega \) et le dernier montré dans la Réf. [23]. De plus, le SOC dans le champ proche tordu des métamatériaux mérite d'être étudié [40,41,42,43].

Abréviations

CP :

Circulairement polarisé

EM :

Électromagnétique

LH :

Gaucher

LP :

Polarisée linéairement

MMP :

Multipolaire

MP :

Microparticule

NP :

Nanoparticule

SOC :

Couplage spin-orbite