Absorbeur plasmonique chiral de métasurface basé sur une nanostructure bicouche en demi-cercle torsadé à fréquence optique

Introduction

La chiralité, en tant que phénomène omniprésent qui fait référence à une propriété géométrique d'un objet dépourvu de toute inversion ou symétrie du plan miroir, reste toujours pertinente pour la science et la technologie [1, 2]. Les médias chiraux apparaissent généralement sous deux formes énantiomères symétriques et non superposables sur son image miroir par simple translation ou rotation, et ils présentent toujours une réponse différente à la polarisation circulaire droitière et gauche (RCP, "+", et LCP, "−") voyant [1]. Le dichroïsme circulaire (CD) de la lumière à polarisation circulaire (CP) provenant des milieux chiraux est l'une des propriétés chiroptiques les plus uniques. L'effet CD fait référence à une réponse différente des lumières RCP et LCP dans les milieux chiraux, ce qui a de larges perspectives d'application en biologie, sciences médicales, chimie, ainsi que dans les dispositifs optoélectroniques liés à la polarisation [3,4,5]. Cependant, l'effet CD des matériaux naturels est plutôt faible, ce qui entrave considérablement son application pratique. Les métasurfaces, en tant que sous-classe de métamatériaux constitués d'une monocouche ou de structures planes à quelques couches, sont très prometteuses pour la manipulation arbitraire des ondes électromagnétiques (EM) ou de la lumière [6,7,8,9,10]. En particulier, la métasurface chirale (CMS) est capable d'améliorer les effets optiques chiraux de plusieurs ordres de grandeur.

Les CMS ont suscité un énorme intérêt car ils pourraient présenter des propriétés EM exotiques, notamment un indice de réfraction et une activité optique négatifs [11, 12], une transmission asymétrique [13, 14], un effet CD géant [15,16,17], une conversion de polarisation [18, 19], et la manipulation du front d'onde [20, 21] etc. Depuis lors, diverses structures CMS (telles que l'anneau fendu, le fil en spirale, le gammadion, la forme en L, etc.) rehaussement sélectif du champ pour la lumière LCP ou RCP [22,23,24,25,26,27,28,29,30,31,32,33]. Cependant, la plupart des conceptions précédentes de ces CMS se concentrent sur les performances de la chiralité en transmission, tandis que beaucoup moins d'attention a été accordée à la réflexion/absorption pour les lumières CP qui sont tout aussi importantes dans les applications d'ingénierie. Il est bien connu que la plupart des études sur les absorbeurs précédents sont appliquées à la lumière à polarisation linéaire, alors que de telles conceptions pour les lumières CP sont rarement étudiées. En fait, les CMS pourraient également être utilisés pour construire de nouveaux absorbeurs pour les lumières CP [25, 26, 29, 30, 31, 32, 33]. Par exemple, Li et al. [25] ont proposé un absorbeur ultra-mince basé sur les fils en forme de L, qui ne peut atténuer l'onde LCP que dans la région des micro-ondes. Wang et al. [29] ont démontré qu'un métamiroir chiral peut refléter presque toute la lumière LCP, tout en absorbant totalement la lumière RCP dans la région infrarouge. Tang et al. [30] ont proposé un absorbeur avec des résonateurs en forme de , qui peut réaliser une absorption sélective pour différentes lumières CP dans le visible. Ensuite, des absorbeurs chiraux dans le proche infrarouge avec une métasurface plasmonique ont été proposés et démontrés comme absorbant sélectivement la lumière LCP ou RCP. Cependant, l'absorbance de la plupart des CMS est inférieure à 90 %. Ainsi, une conception efficace de l'absorbeur de métasurface chiral (CMSA) avec une absorption sélective élevée est hautement souhaitable.

Dans ce travail, nous présentons un type de CMSA hautement efficace basé sur une nanostructure en demi-cercle torsadée à quatre couches fonctionnant dans le proche infrarouge et le visible. Un tel CMSA pourrait atteindre sélectivement plus de 90 % d'absorption pour différentes lumières CP à différentes fréquences de résonance. En raison de la forte absorption sélective du CMSA proposé, une valeur CD élevée d'environ 0,9 peut être obtenue en conséquence. Le mécanisme physique sous-jacent à l'absorption sélective pour différentes lumières CP a été analysé en détail par des distributions de champ électrique. De plus, les influences des paramètres géométriques des cellules unitaires sur l'absorption sélective ont également été étudiées systématiquement. On peut raisonnablement croire que les résultats de ce travail peuvent guider la conception de CMSA avec une forte absorption et un effet CD pour de nombreuses applications pratiques telles que l'absorbeur thermique, les dispositifs de communication optique, le photodétecteur, les filtres optiques, l'imagerie et les hologrammes.

Unit-Cell Design

La figure 1 présente le diagramme schématique du CMSA proposé, qui est constitué d'un réseau périodique avec une nanostructure en demi-cercle torsadée. La nanostructure en demi-cercle torsadée quadruple de chaque côté du substrat diélectrique est positionnée de sorte que chacune pivote de 90 ° par rapport à son voisin, et le côté inférieur de chaque nanostructure en demi-cercle est également tourné de 90 ° par rapport à celle du haut, comme indiqué dans la figure 1b. De la même manière que dans la conception précédente [32], les quatre nanostructures en demi-cercle supérieures sont reliées à celle du bas par des cylindres en cuivre, et le rayon du cylindre en cuivre est le même que la largeur du fil en demi-cercle, ce qui peut augmenter le couplage conducteur. La nanostructure en demi-cercle torsadé peut être considérée comme un système de résonateur couplé, où les fortes réponses chirales proviennent du couplage inductif électrique et magnétique entre les deux demi-cercles connectés torsadés [34, 35]. Cette nanostructure simple en demi-cercle torsadé avec des symétries miroir est conçue dans les couches supérieure et inférieure permettant au CMSA proposé d'améliorer la chiralité.

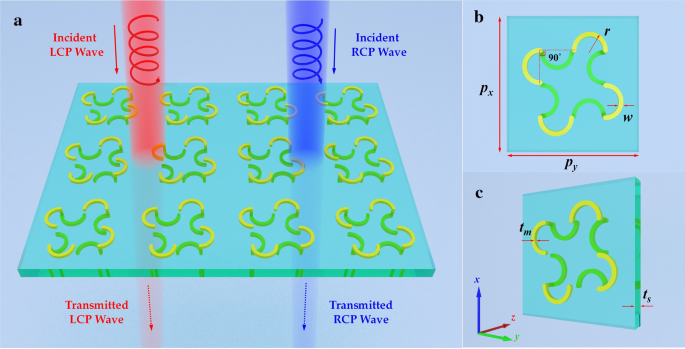
Schéma du CMSA conçu :a tableau périodique, b , c la vue de face et en perspective de la nanostructure à cellules unitaires. Les longueurs périodiques le long de x - et y- les directions des axes sont toutes deux de 600 nm, et les lumières incidentes normales du CP se propagent le long du z -direction de l'axe

La cellule unitaire globale du CMSA proposé présente une rotation quadruple (C₄ ) symétrie pour la direction de propagation de la lumière. Le substrat diélectrique de la couche intermédiaire est constitué d'un diélectrique sans perte MgF₂ avec une permittivité relative de 1,9. Les nanostructures métalliques chirales ont été sélectionnées comme de l'or, et le paramètre matériau peut être décrit par le modèle de Drude [36]. Les paramètres de structure optimisés de la maille élémentaire sont donnés comme :p _x = p _y = 600 nm, r = 70 nm, w = 40 nm, t _s = 120 nm, t _m = 30 nm. La maille élémentaire du CMSA est périodique le long du x- et y -des directions d'axe avec des périodes de 600 nm pour éviter la diffraction lorsque la fréquence de la lumière d'incidence atteint 500 THz. Pour vérifier l'efficacité du CMSA proposé, les simulations EM haute fréquence pleine onde ont été effectuées sur la base de la méthode des éléments finis (FEM) en utilisant le solveur de domaine fréquentiel dans CST Microwave Studio. Une fois que la nanostructure de cellules unitaires CMSA, les conditions aux limites appropriées, la taille du maillage et la plage de fréquences ont été raisonnablement définies, la simulation du domaine fréquentiel peut être lancée.

Résultats et discussions

Les coefficients de transmission de co-polarisation simulés (t ₊₊ (ω), t _− − (ω)) et les coefficients de réflexion (r ₊₊ (ω), r _− − (ω)) pour les lumières incidentes LCP et RCP normales sont présentés sur la figure 2. Deux modes de résonance plasmonique chiraux (mode 1 et mode 2) ont pu être observés à des fréquences de f. ₁ = 288,5 THz et f ₂ =404 THz, respectivement. On peut observer que le coefficient de réflexion de co-polarisation r ₊₊ (ω) pour RCP et r _− − (ω) pour les lumières LCP sont égales ; et les deux sont inférieurs à 0,4 dans toute la gamme de fréquences intéressée. De plus, les magnitudes de r ₊₊ (ω) et r _− − (ω) diminue jusqu'à environ 0,15 aux résonances, indiquant l'adaptation d'impédance entre le CMSA et l'espace libre pour les lumières RCP et LCP. On peut également voir que les coefficients de transmission de co-polarisation t ₊₊ (ω) pour RCP et t _− − (ω) pour les lumières LCP sont significativement différentes aux résonances en raison de la nature chirale du CMSA proposé. Autour du point de fréquence inférieure f ₁ , l'amplitude de t ₊₊ (ω) pour la lumière RCP est d'environ 0,93, ce qui est beaucoup plus élevé que t _− − (ω) pour la lumière LCP qui est d'environ seulement 0,075. Autour du point de fréquence supérieure f ₂ , l'amplitude de t ₊₊ (ω) pour la lumière RCP diminue jusqu'à la valeur minimale de 0,018, tandis que t _− − (ω) pour le LCP est jusqu'à la valeur maximale d'environ 0,92. Cela signifie que seule la lumière incidente RCP peut être sélectionnée pour traverser le CMSA alors que la lumière LCP est interdite à la fréquence inférieure. Comme à la fréquence plus élevée f ₂ , seule la lumière incidente LCP peut être sélectionnée pour traverser le CMSA alors que la lumière RCP est extrêmement interdite. Ainsi, les phénomènes de sélection chirale du CMSA ci-dessus entraîneraient par conséquent une absorption différente pour les lumières RCP et LCP, impliquant l'existence d'une absorption sélective à haut rendement et d'un effet CD géant aux résonances.

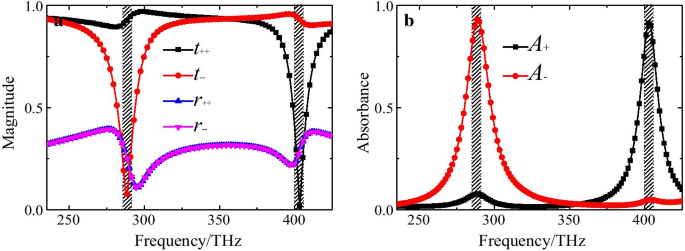
un Coefficients de transmission de co-polarisation simulés (t ₊₊ (ω), t _− − (ω)) et les coefficients de réflexion (r ₊₊ (ω), r _− − (ω)) du CMSA proposé pour les feux LCP et RCP incidents normaux, b l'absorbance correspondante (A ₊ (ω), A ₋ (ω)) pour les voyants LCP et RCP

La figure 2b montre les spectres d'absorbance (A ₊ (ω), A ₋ (ω)) pour les lumières incidentes LCP et RCP. On peut observer que l'absorbance pour les lumières LCP et RCP atteint une valeur maximale d'environ 93,2 % et 91,6 %, tandis que celle des lumières RCP et LCP est réduite à seulement 8,7 % et 4,8 % environ autour des deux résonances ci-dessus, respectivement. . De toute évidence, on peut conclure que le CMSA proposé présente une forte absorption de la lumière LCP et un niveau de transmission assez élevé pour la lumière RCP autour de la fréquence inférieure f ₁ , alors que la condition s'inverse complètement lorsque la fréquence atteint la fréquence de résonance supérieure f ₂ . Cela signifie que le CMSA proposé affiche une absorption sélective pour deux lumières CP avec une maniabilité particulière tout en réfléchissant l'autre à des résonances différentes. En outre, il convient également de souligner que le CMSA a les deux bandes de fréquences d'absorption fortes en utilisant simplement une nanostructure chirale de taille unique, et est raisonnablement supérieur par rapport aux absorbeurs chiraux précédents avec une bande d'absorption isolée dont l'adaptation pour différentes lumières CP dépend fortement de taille de géométrie différente [25, 26, 29, 31,32,33]. Ainsi, la nanostructure chirale conçue peut servir d'absorbeur de lumière LCP parfait à la fréquence inférieure et d'absorbeur de lumière RCP parfait à la fréquence plus élevée. Il convient de noter que les performances d'absorption sélective du CMSA proposé se détérioreront avec l'augmentation de l'angle incident (incidence oblique), en raison de la résonance plasmonique multipolaire d'ordre supérieur (non illustré). De plus, on peut déduire que l'absorption sélective chirale élevée pour les lumières CP entraînera un effet CD géant dans le CMSA proposé.

La différence d'absorption ou de transmission entre les lumières LCP et RCP peut être caractérisée par le paramètre CD Δ . La figure 3a présente le spectre CD du CMSA, où les principaux pics du paramètre CD sont respectivement d'environ 0,85 et 0,91 à deux fréquences de résonance ; ce qui est bien supérieur aux nanostructures chirales rapportées [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32, 37,38,39,40, 41,42]. L'effet CD géant est causé par la forte chiralité du CMSA et peut donc être appliqué comme un polariseur circulaire transparent. Pour étudier plus en détail la pureté CP du CMSA appliqué en tant que polariseur circulaire, nous donnons l'angle d'ellipticité η et angle de rotation d'azimut de polarisation θ comme le montre la figure 3b. On peut trouver que la valeur de η est d'environ 40,4° et − 43,9°, tandis que la valeur de θ est d'environ 0° aux fréquences inférieures et supérieures, respectivement. Cela signifie que les lumières transmises présentent des caractéristiques RCP et LCP importantes après avoir traversé la dalle CMSA aux deux fréquences de résonance. Il convient de noter que ce polariseur circulaire basé sur CMSA avec la pureté CP la plus élevée est valable pour toutes les lumières à polarisation arbitraire en raison de son C₄ élevé. symétrie de la maille élémentaire. Ainsi, on peut raisonnablement penser que le polariseur circulaire homogène est réalisé avec notre nanostructure chirale conçue.

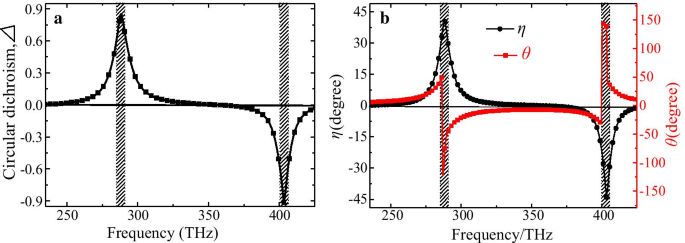
Les paramètres optiques relatifs calculés du CMSA proposé pour les lumières incidentes normales LCP et RCP, a le paramètre CD Δ , b angle d'ellipticité η et angle de rotation d'azimut de polarisation θ

Afin de bien comprendre l'absorption sélective et l'effet CD géant du CMSA, nous avons récupéré l'indice de réfraction Re(n ), Re(n ₋ ), Re(n ₊ ) et le paramètre chiral Re(κ ) en utilisant une procédure d'extraction standard à partir des coefficients de transmission et de réflexion des lumières CP [43, 44], comme illustré sur les Fig. 4a, b. Il est clair que deux résonances liées à la forte chiralité émergent dans le CMSA conçu. La résonance de fréquence inférieure se produit autour de 288,5 THz tandis que la fréquence supérieure se situe à 404 THz, ce qui correspond aux fréquences caractéristiques de l'absorption sélective et des pics CD. Comme le montre la figure 4a, le Re(n ) est négatif avec des amplitudes maximales de − 2.3 et − 1.1, et le Re(κ ) va jusqu'à des magnitudes maximales de 6,4 et − 5,1 autour des deux fréquences de résonance ci-dessus. Il est clair que le paramètre chiral κ contribue également à la réfraction négative des lumières RCP et LCP. La forte chiralité peut facilement pousser l'indice de réfraction de la lumière RCP/LCP à devenir négatif aux résonances en raison de la relation de n _± = n ± κ . Ainsi, comme le montre la figure 4b, le Re(n ₋ ) pour la lumière LCP et Re(n ₊ ) pour la lumière RCP est négatif de 286,2 THz à 291 THz et de 400,2 THz à 404 THz, respectivement. De plus, le Re(n ₋ ) et Re(n ₊ ) sont jusqu'aux valeurs négatives maximales de − 8,6 et − 6,3 à deux résonances ci-dessus, respectivement. Il révèle que l'absorption sélective élevée ainsi que l'effet CD géant du CMSA proposé sont associés à la propriété de réfraction négative des lumières LCP et RCP.

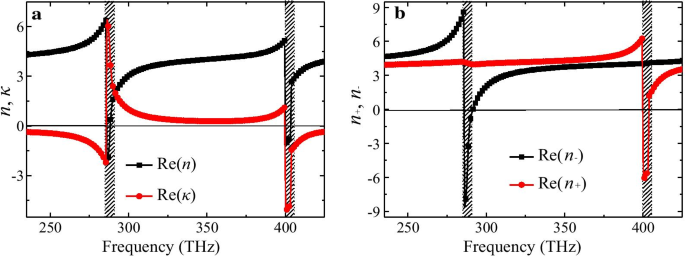
Les paramètres chiraux relatifs récupérés du CMSA proposé :a parties réelles de l'indice de réfraction moyen Re(n ) et le paramètre chiral Re(κ ), b indice de réfraction Re(n ₋ ), Re(n ₊ ) pour les feux LCP et RCP

Pour dévoiler davantage l'origine de l'absorption sélective associée à l'effet CD géant du CMSA proposé, le champ électrique (E _z ) les distributions de la cellule unitaire pilotée par les lumières RCP et LCP à 288,5 THz et 404 THz ont été étudiées. Il est connu que l'excitation de la résonance des plasmons de surface produira des champs dipolaires oscillants puisque la nanostructure en demi-cercle présente de petits diamètres par rapport à la longueur d'onde incidente des différentes lumières CP [45,46,47,48]. Lorsque la lumière RCP ou LCP illumine la nanostructure en demi-cercle, on peut raisonnablement penser que l'absorption sélective et l'effet CD géant apparaîtront dans le CMSA proposé et entraîneront par conséquent la distribution différente des composants du champ électrique et du champ magnétique dans chaque couche [48 ,49,50,51,52,53].

La figure 5 montre le champ électrique (E _z ) distributions du CMSA proposé piloté par les lumières RCP et LCP à différentes fréquences de résonance. Les tracés détaillés du champ électrique (E _z ) les distributions sur les nanostructures en demi-cercle montrent clairement la nature de chaque mode plasmonique de surface [54]. La région rouge et bleue sur la nanostructure en demi-cercle des couches supérieure et inférieure présente les accumulations de charges positives et négatives sous excitation lumineuse RCP et LCP. Les charges positives et négatives sont séparées et principalement accumulées aux coins de chaque nanostructure en demi-cercle, agissant comme une oscillation dipolaire électrique. On peut observer que la puissance dipolaire électrique est beaucoup plus forte que la puissance magnétique dans la nanostructure en demi-cercle conçue, révélant la prédominance des oscillations dipolaires électriques. L'absorption sélective et l'effet CD géant générés aux résonances sont dus à la puissance dipolaire évidente différente sous excitation LCP et RCP. Ici, une méthode simplifiée avec des moments dipolaires électriques équivalents a été appliquée, qui considère les vibrations de charge de quatre nanostructures en demi-cercle dans chaque couche comme une vibration dipolaire [48,49,50]. Selon la théorie de Born-Kuhn [47, 48], le mode qui s'hybride à partir de deux dipôles avec la même direction de champ électrique est appelé mode de liaison, tandis que l'autre qui est hybride à partir de deux dipôles avec 90° ou direction croisée est noté comme mode anti-collage. Comme le montre la figure 5a1, b1, sous un éclairage RCP à une fréquence de résonance de f ₁ =288,5 THz, les champs dipolaires électriques dans les couches supérieure et inférieure montrent les directions croisées et forment un mode anti-liaison, et par conséquent résultant en la transmission élevée de la lumière RCP selon le modèle de Born-Kuhn. Comme le montre la figure 5c1, d1, sous un éclairage LCP, on peut voir que la distribution du champ électrique de CMSA peut être considérée comme un hybride du mode de liaison entre les couches supérieure et inférieure, qui est composé de deux équivalents électriques moments dipolaires avec la même direction, résultant en un niveau d'absorption élevé de la lumière LCP. Ainsi, les modes de liaison et d'anti-liaison provoquent une énergie de résonance différente et une transmission et une absorption différentes des nanostructures chirales à la fréquence inférieure sous l'éclairage des lumières LCP et RCP (voir Fig. 2). Comme le montre la figure 5a2, b2, c2, d2, sous l'éclairage des lumières RCP et LCP à une fréquence de résonance de f ₂ =404 THz, les champs dipolaires électriques dans les couches supérieure et inférieure montrent respectivement les mêmes directions (mode de liaison) et directions croisées (mode anti-liaison), ce qui entraîne par conséquent un niveau d'absorption élevé pour la lumière RCP et une transmission élevée pour la lumière LCP. Par conséquent, on peut voir que l'absorption sélective et l'effet CD à deux fréquences différentes sont principalement attribués aux modes de liaison et anti-liaison, qui sont induits par le couplage hybride des moments dipolaires électriques des couches supérieure et inférieure.

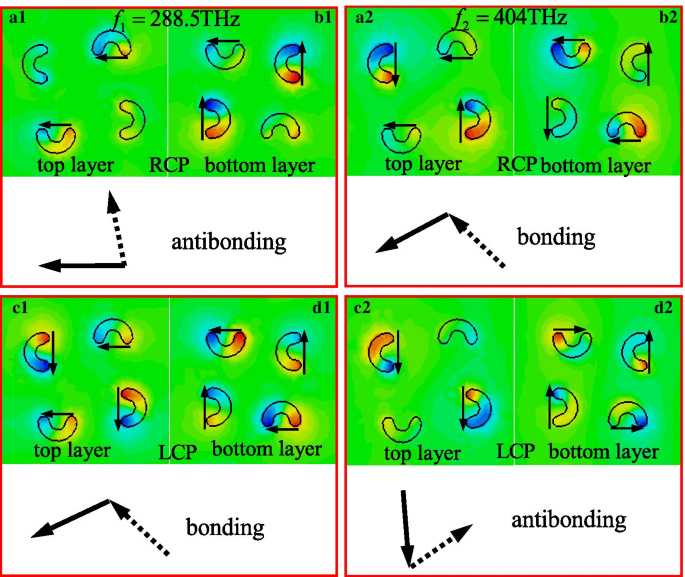
Le champ électrique (E _z ) distributions de mailles unitaires du CMSA proposé induites par le (a1 , b1 , a2 , b2 ) RCP et (c1 , d1 , c2 , d2 ) LCP s'allume à différentes fréquences de résonance :(a1 –d1 ) f ₁ = 288,5 THz, (a2 –d2 ) f ₂ = 404 THz. Les flèches en trait plein noir (ligne pointillée) indiquent les moments dipolaires électriques équivalents sur la couche supérieure (inférieure) de la nanostructure chirale proposée

Dans ce qui suit, nous étudions les influences des paramètres géométriques de la maille élémentaire sur les propriétés d'absorption du CMSA proposé. La figure 6 montre les spectres d'absorbance simulés pour les lumières LCP et RCP, et les fréquences de résonance (f ₋ , f ₊ ) avec différents paramètres géométriques (r , w , t _m , et t _s ) de la maille élémentaire. Pour la nanostructure conçue, une variation spectrale intéressante de la propriété d'absorption sélective dépendante des paramètres, qui est évidemment multifactorielle compétitive et complexe, a pu être observée. Dans cette étude, les paramètres géométriques du groupe témoin sont r = 70 nm, w = 40 nm, t _m = 30 nm, et t _s = 120 nm, et en changeant un paramètre à la fois.

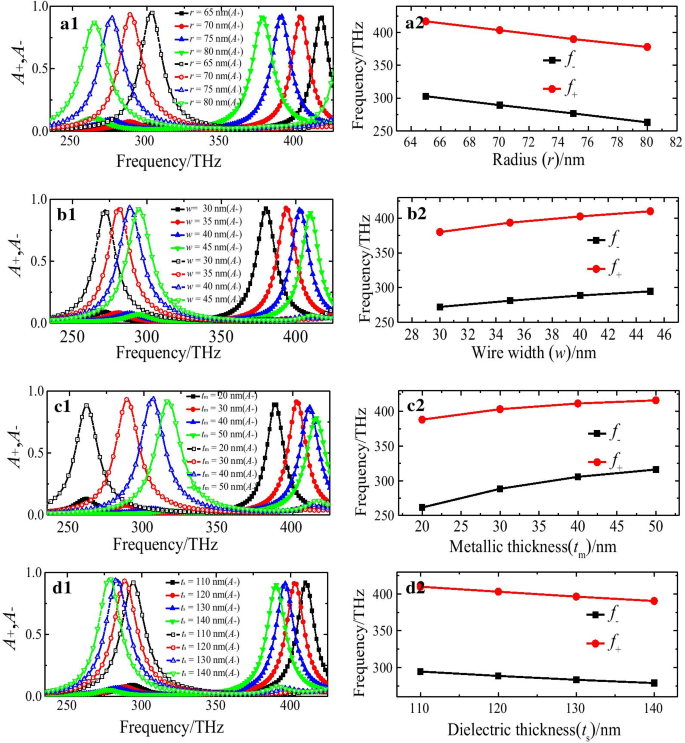
Le simulé (a1 –d1 ) spectres d'absorbance et (a2 –d2 ) fréquences de résonance (f ₋ , f ₊ ) des lumières LCP et RCP du CMSA proposé avec différents paramètres géométriques :(a1 , a2 ) rayon (r ), (b1 , b2 ) largeur de fil (w ), et (c1 , c2 ) épaisseur (t _m ) de nanostructure en demi-cercle, (d1 , d2 ) épaisseur du substrat diélectrique (t _s )

La nanostructure en demi-cercle avec les différents r (r = 65 nm, 70 nm, 75 nm et 80 nm) ont d'abord été calculés, tandis que les autres paramètres sont fixés comme le montre la figure 6a1, a2. Quand augmente r , les fréquences de résonance f ₋ pour LCP et f ₊ pour RCP, les lumières diminuent progressivement, ce qui peut être interprété par l'équivalent LC théorie des circuits de résonance [55, 56]. Les fréquences de résonance (f ₋ , f ₊ ) pour les lampes LCP et RCP, l'éclairage peut être exprimé sous la forme \(f_{ \mp } =\frac{1}{{2\pi \sqrt {LC} }}\), où la capacité équivalente C et inductance L sont principalement déterminés par les paramètres géométriques du CMSA proposé. Le L augmentera avec l'augmentation du r , entraînant ainsi la diminution des fréquences de résonance (f ₋ , f ₊ ). De plus, comme le montre la figure 6a1, lorsque augmente r , l'absorbance de la lumière LCP diminuera progressivement tandis que celle de la lumière RCP sera pratiquement inchangée. La figure 6b1, b2 montre les spectres d'absorbance des lumières LCP et RCP lors du changement de w de 30 à 45 nm par pas de 5 nm, tandis que les autres paramètres sont maintenus inchangés. On peut voir que les fréquences de résonance (f ₋ , f ₊ ) pour les voyants LCP et RCP augmentera progressivement avec l'augmentation du w . Evidemment, l'augmentation des fréquences de résonance (f ₋ , f ₊ ) est principalement due à la diminution du C . L'absorbance de la lumière LCP augmentera d'abord puis diminuera légèrement, tandis que celle de la lumière RCP diminuera progressivement en augmentant w , comme le montre la figure 6b2. Comme le montre la Fig. 6c1, c2, nous présentons les spectres d'absorbance et les fréquences de résonance (f ₋ , f ₊ ) des voyants LCP et RCP avec des t variables _m de 20 à 50 nm par pas de 10 nm et autres paramètres fixés. Il existe des cas similaires au changement de w , quand augmente t _m , la fréquence de résonance (f ₋ ) pour la lumière LCP augmente de manière significative, et celle pour la lumière RCP augmente légèrement. Dans ce cas, le L diminuera avec l'augmentation du t _m , entraînant ainsi l'augmentation des fréquences de résonance (f ₋ , f ₊ ). De plus, l'absorbance des lumières LCP et RCP augmentera d'abord puis diminuera en augmentant t _m , comme le montre la figure 6c2. Enfin, nous avons illustré les spectres d'absorbance et les fréquences de résonance (f ₋ , f ₊ ) pour les lampes LCP et RCP avec différents t _s (t _s = 110 nm, 120 nm, 130 nm et 140 nm), tandis que les autres paramètres restent inchangés, comme le montre la figure 6d1, d2. On peut observer que lorsque augmente t _s , l'absorbance du LCP augmentera progressivement, tandis que celle de la lumière RCP diminuera légèrement, comme le montre la figure 6d1. De plus, les fréquences de résonance (f ₋ , f ₊ ) pour les deux lumières LCP et RCP diminuent progressivement lorsque augmente t _s , comme le montre la figure 6d2. Dans ce cas, le C augmentera quand augmente t _s , entraînant ainsi la diminution des fréquences de résonance (f ₋ , f ₊ ). On peut conclure que les fréquences de résonance (f ₋ , f ₊ ) et le niveau d'absorption des lumières RCP et LCP sont sensibles aux paramètres géométriques de la cellule unitaire de la nanostructure chirale conçue. Ainsi, les propriétés d'absorption sélective du CMSA proposé peuvent être ajustées dynamiquement en faisant varier les paramètres de structure.

Conclusion

En conclusion, un CMSA basé sur une nanostructure en demi-cercle torsadé à quatre couches a été proposé pour obtenir une absorption sélective chirale presque parfaite pour les lumières RCP et LCP ainsi qu'un effet CD géant dans les régions proche infrarouge et visible. Les résultats de la simulation montrent que l'absorbance sélective chirale pour les lumières RCP et LCP est supérieure à 90 %, et la magnitude CD pourrait atteindre 0,91. Selon les paramètres EM effectifs récupérés, on peut constater que l'absorption de fréquence inférieure et l'effet CD sont tous deux associés aux propriétés de réfraction négative de la lumière LCP, tandis que le cas de fréquence plus élevée concerne la lumière RCP. Les distributions de champ électrique indiquent que les propriétés d'absorption sélective chirale et l'effet CD géant du CMSA proviennent principalement des modes de liaison et d'anti-liaison qui sont induits par le couplage hybride des moments dipolaires électriques des couches supérieure et inférieure. De plus, les fréquences de résonance et le niveau d'absorption sélective chirale du CMSA peuvent être réglés en modifiant les paramètres géométriques de la cellule unitaire. Par conséquent, on peut raisonnablement conclure que la conception du CMSA est prometteuse pour de futures applications dans les domaines du filtre optique, de l'imagerie chirale, du polariseur circulaire, de la détection et des communications optiques.

Section de méthode numérique

Simulations FEM :Des simulations EM pleine onde ont été effectuées sur la base d'une méthode des éléments finis (FEM). En simulation, les propriétés électriques de l'or sont décrites par le modèle de Drude comme [36] :

où ω _p = 1,37 × 10 ¹⁶ rad/s est la fréquence du plasma et γ = 8.04 × 10 ¹³ rad/s est la fréquence de collision de l'or dans la gamme de fréquences optiques. En simulation, la condition aux limites de la cellule unitaire a été appliquée le long de x - et y -axe et les deux lumières propres CP ont été utilisées directement. Les lumières CP à large bande sont utilisées comme sources d'excitation et sont normalement à travers la cellule unitaire de la nanostructure chirale conçue à partir du - z à + z direction. Ensuite, les coefficients de réflexion et de transmission des lumières LCP et RCP peuvent être obtenus. Généralement, l'absorbance notée A ₋ (ω)/A ₊ (ω) pour les voyants LCP/RCP peut être exprimé par [17, 32] :A ₋ (ω) = 1 − R _− − (ω) − T _− − (ω) = 1 − |r _− − (ω)| ² − |t _− − (ω)| ² , A ₊ (ω) = 1 − R ₊₊ (ω) − T ₊₊ (ω) = 1 − |r ₊₊ (ω)| ² − |t ₊₊ (ω)| ² , respectivement. Les coefficients de transmission de co-polarisation t _− − (ω) sont pour le LCP et t ₊₊ (ω) pour les lumières RCP, tandis que r _− − (ω) et r ₊₊ (ω) sont les coefficients de réflexion de co-polarisation, respectivement. Il est à noter que les coefficients de transmission de polarisation croisée (t ₊₋ (ω), t ₋₊ (ω)) et les coefficients de réflexion (r ₊₋ (ω), r ₋₊ (ω)) pour les lampes LCP et RCP sont suffisamment petites pour être négligées (< 0,01) en raison du C élevé ₄ symétrie de la cellule unitaire de la nanostructure chirale conçue. De plus, l'effet CD est induit par l'absorption sélective de deux lumières CP, qui peut être exprimée par :△ =|t ₊₊ (ω)| − |t _− − (ω)| [14, 29]. L'ellipticité et l'activité optique sont des paramètres importants pour évaluer la chiralité de la nanostructure chirale conçue. The ellipticity characterizes the polarization state of transmitted lights of the chiral nanostructure, which is described by ellipticity angle η  = arctan[(|t ₊₊ (ω)| − |t _− − (ω)|) / (|t ₊₊ (ω)| +|t _− − (ω)|)]. While the optical activity represents the rotation property of polarization plane of a transmitted linear polarization light respect to the incident one, which is described by the polarization azimuth rotation angle θ  = [arg(t ₊₊ (ω))  − arg(t _− − (ω))]/2.

Availability of data and materials

The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.

Abréviations

CMS:

Chiral metasurface

CMSA:

Chiral metasurface absorber

RCP:

Right-handed circular polarization

LCP:

Left-handed circular polarization

CD:

Circular dichroism

EM:

Electromagnetic

CP:

Circular polarization